不規則波與順流相互作用的數值模擬與不確定度分析

姚 順，馬 寧，丁俊杰，顧解忡

(上海交通大學 海洋工程國家重點實驗室；船舶海洋與建筑工程學院，上海 200240)

隨機不規則波浪和水流廣泛存在于實際海洋環境中，波流相互作用極其常見.攜帶大量能量的海流使波浪要素發生變形，進而導致海域海況趨于復雜與危險.近年來，由波流相互作用引起的船舶失事、海洋結構物毀壞等事故時有發生，因此，研究波流的相互作用，特別是不規則波與流的相互作用具有重要的現實意義.

Tayfun等[1]依據Gram-Charlier(GC)模型給出加入四階聯合累積量修正的GC分布，研究了非線性對不規則波的波高概率分布的影響.Soltanpour等[2]和Wei等[3]通過一系列實驗分別研究了波流相互作用下波浪在泥床上的耗散情況和目標橋梁基礎與上部結構的水動力響應特性.Jiang等[4]和Liu等[5]利用計算流體力學(CFD)軟件建立數值波浪水池，模擬了規則波、不規則波與淹沒式防波堤及半潛式圓柱體的相互作用，并將模擬結果與實驗結果進行對比，研究結果表明不同波參數的入射波對波浪與結構物的相互作用影響顯著.Dong[6]建立了一套新理論用于描述有限水深條件下，強剪切流作用時的波流相互作用現象，然后用3個實際案例對計算結果進行驗證，獲得了強剪切流作用下目標波浪的波浪特性.但文獻[2-6]對比試驗數據與數值模擬結果進行驗證的方法從本質上說是定性的.為了定量評價CFD數值模擬結果的可靠性，CFD不確定度分析逐漸受到學者的關注.Zhu等[7]和Deng等[8]分別對船模橫搖運動和小水線面雙體船在波浪中的縱向運動進行了數值模擬與不確定度分析.Bachynski等[9]對單樁海上風電機組在不規則波作用下的響應進行了數值模擬，并對波面高度和單樁彎矩的數值模擬結果進行了不確定度分析.Coe等[10]和Bai等[11]則分別對波浪能轉換器的線性動力學模型和聚焦波波面升高時歷結果進行了不確定度分析.然而文獻[7-11]并沒有進行波流相互作用模型的不確定度分析，水流對計算結果不確定度的影響研究更是鮮有出現.該問題的難點在于開展波流相互作用試驗時很難保證造波精度.丁俊杰等[12]對上海交通大學風洞循環水槽的消波裝置進行了改進，改進后該水槽能滿足不規則波與順流相互作用的試驗要求.由于水槽造波設備的限制，逆流中的造波實驗暫未實施，雖然逆流中的波浪具有更強的非線性和不穩定性，但順流條件是大多海洋結構物設計的基本要求條件，所以本文將聚焦于順流條件下的波浪生成、波流相互作用及不確定度分析.

本文開展均勻流與不規則波相互作用的物理試驗，基于雷諾平均Navier-Stokes(RANS)方程建立數值波浪水池，求解不規則波與均勻流相互作用問題.對有義波高、平均周期的計算結果開展不確定度分析，并詳細探討了均勻流對不規則波的運動學及能量特性的影響情況.通過不確定度分析對順流作用下的不規則波模型進行驗證，最后得出順流對計算結果不確定度的影響規律.

1 試驗安排

波流相互作用試驗的目的是獲取不同工況下指定位置處不規則波的波高時歷曲線.試驗布置如圖1所示，其中vC為流速.試驗使用的設備包括：循環水槽、造波機、消波裝置、流速計、浪高儀及高清攝像機等.造波機為一臺搖擺式造波機，兩側緊貼水槽槽壁，設定造波板振幅和周期后即可生成規則波、JONSWAP譜不規則波與聚焦波等波浪.消波裝置是一種多層變角度開孔折彎板透水消波裝置[13]，放置在距造波端6 m處，能夠保證較高的透水和消波效率.采用畢托管測量水流流速，其原理是通過流體壓力與靜壓力之間的壓差來計算流速.浪高儀為電容式浪高儀，量程為300 mm，解析度為0.05 mm，最大采樣頻率為100 Hz.試驗共布置5個浪高儀，1#、2#和3#浪高儀布置在消波裝置前側，分別距造波端3.2、3.6、4.0 m，且分別距水槽左端1.0、2.0、1.5 m；4#和5#浪高儀沿y方向平行放置于消波裝置后側，距造波端6.7 m，且分別距左側槽壁1.0、2.0 m.

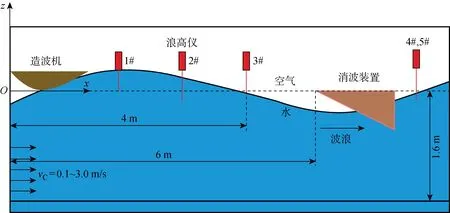
圖1 波流相互作用試驗布置Fig.1 Arrangement of wave-current interaction test

2 數值模型與試驗驗證

2.1 數值模型

在計算流體力學商業軟件STAR-CCM+中建立數值波浪水池對不規則波與流相互作用問題進行求解，求解過程參考文獻[14].該軟件采用有限體積法求解，湍流模型選擇RANS方程，可表示為

(1)

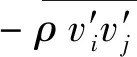
(2)

μt為湍流黏度；τij為Kronecker函數；k為湍動能.可采用Renormalization-Group(RNG)k-ε模型求解湍流黏度和湍動能，進而獲得Reynolds應力.

基于物理水槽在STAR-CCM+中構造二維數值波浪水池，水池的長寬高分別為8.0、0.1、2.0 m，水深為1.6 m.為簡單起見，選擇源項造波法造波，造波起點與坐標原點重合，x軸正向為波浪傳播方向；采用軟件庫函數Current設定水體速度以實現穩定造流.在尾部2 m處添加阻尼消波段，其主要原理與參數參考文獻[15].根據試驗中使用的多層變角度開孔折彎板透水消波裝置[13]等比例建模，并將消波裝置放置在阻尼消波段左側以達到消波目的.空間離散采用二階迎風格式，壓力和速度耦合求解采用SIMPLE算法.

為保證模擬精度，x、y、z方向對應的最小網格尺寸分別為0.01、0.1、0.0015 m，時間步長為0.001 s，滿足x方向最小網格尺度不大于1/100波長，z方向最小網格尺度不大于1/20波高，時間步長不大于1/1200周期的要求[12].自由液面捕捉采用流體體積(VOF)法.數值波浪水池如圖2所示，其中，AC和BD邊界分別選擇速度入口和壓力出口，AB邊界為無滑移固壁邊界，CD邊界為速度入口邊界，兩側邊界選用對稱邊界.

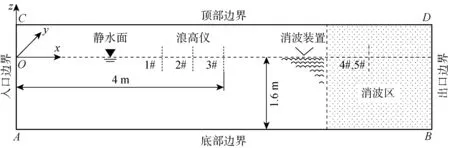
圖2 數值波浪水池Fig.2 Numerical wave flume

本文不規則波的模擬選擇目前廣泛使用的JONSWAP譜.JONSWAP譜可采用有義波高和譜峰周期表征其能量譜密度，可表示為

(3)

式中：H1/3為有義波高；Tp為譜峰周期；ω為波浪圓頻率；γ為譜峰提升因子，此處取3.3；α為無因次參數，此處取 0.049 7；ψ為峰形參數.ωp為ω對應的譜峰圓頻率，當ω≤ωp時，取ψ=0.07；當ω>ωp時，取ψ=0.09.

波流相互作用試驗與數值模擬工況如表1所示，其中：TES和NUM分別表示對該工況進行試驗或數值模擬.每組試驗或模擬時長為200 s(約150個波浪周期).每個工況重復3組，通過試驗或數值模擬獲得自由液面處波高時歷曲線后，計算出有義波高和所有波浪周期求平均后的平均周期，然后通過快速Fourier變換(FFT)求取能量譜密度函數(下文稱能量譜)以及譜峰周期等波參數，作為該工況的統計數據.為表述方便，下文將工況(F)1(vC=0 m/s)稱為無流工況，F2(vC=0.3 m/s)稱為順流工況，F3～F5(vC=-0.1、-0.2、-0.3 m/s)稱為逆流工況.

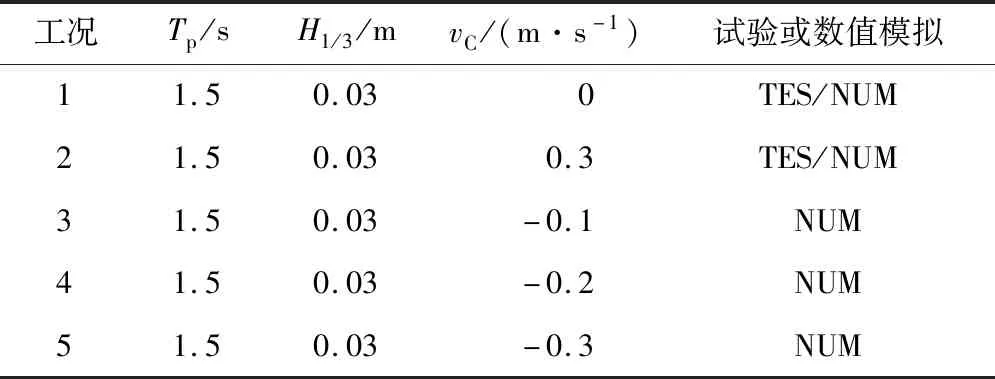
表1 波流相互作用試驗與數值模擬工況Tab.1 Test and numerical conditions of wave-current interaction

2.2 試驗驗證

在x=4 m自由液面處，F1和F2中測得的能量譜密度函數曲線如圖3所示.由圖3可知，由F1和F2數值模擬獲得的H1/3、Tp、能量譜峰值等譜形參數與理論值和試驗值相差不大.當vC=0 m/s時，數值模擬得到的能量譜曲線低頻部分與目標譜吻合，且曲線光順；高頻段(5～6 rad/s)的部分曲線存在尖劈，說明自由液面存在一定的非線性現象.當vC=0.3 m/s時，數值模擬得到的Tp略小于試驗值而H1/3和能量譜峰值略大于試驗值，這是由于數值模型的造波方法為源項造波法，沒有考慮實際造波機與水流的相互作用影響導致的.

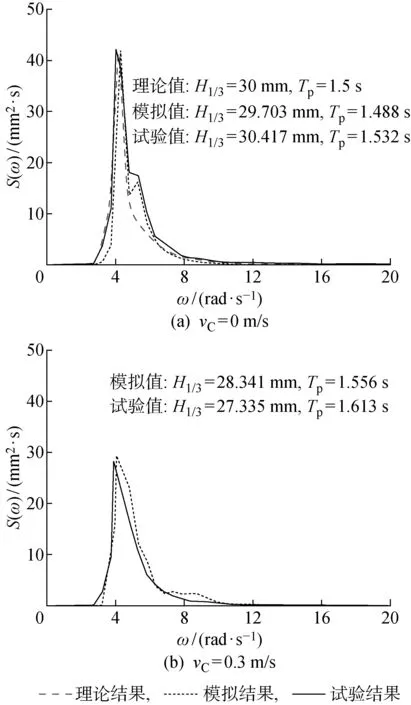
圖3 不同流速下的能量譜曲線對比Fig.3 Comparison of energy spectrums at different current velocities

3 數值模擬結果及不確定度分析

3.1 結果分析

偏度Sk是描述波高概率密度曲線相對于平均值不對稱程度的特征參數，可以反映波浪的二階非線性特征，由下式計算：

(4)

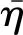
(5)

式中：H為波高；m0為波浪頻譜的零階矩.在深水條件下，Tayfun等[1]推導出GC級數形式的GC分布，在波高為兩倍波幅的假設下，波高概率分布為

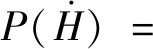
(6)

不同流速下不規則波的有義波高、譜峰周期、偏度值的數值結果及波高概率分布曲線的模擬值與試驗值如圖4所示，尾部極端值表征波高極大值.由圖4可知，順流時不規則波的有義波高和偏度值小于無流工況的結果，譜峰周期的變化規律則相反，順流的作用導致譜峰周期有所增大.F1和F2的波高概率分布曲線模擬結果與試驗結果比較一致；由F1和F2試驗獲得的波高極大值略小于數值模擬結果，這一誤差同樣是由于試驗過程中造波機與水流的相互作用導致了造波效率下降所引起的.進一步分析可知，當vC=0、0.3 m/s時，除了尾部的極端值以外，波高概率分布比較符合Rayleigh分布而遠離GC分布，不規則波的非線性程度較小；由模擬得到的概率分布尾部極端值從1.32H1/3(vC=0 m/s)減小到1.30H1/3(vC=0.3 m/s)，可見順流作用下可能的極端波高相對無流情況有所減小.

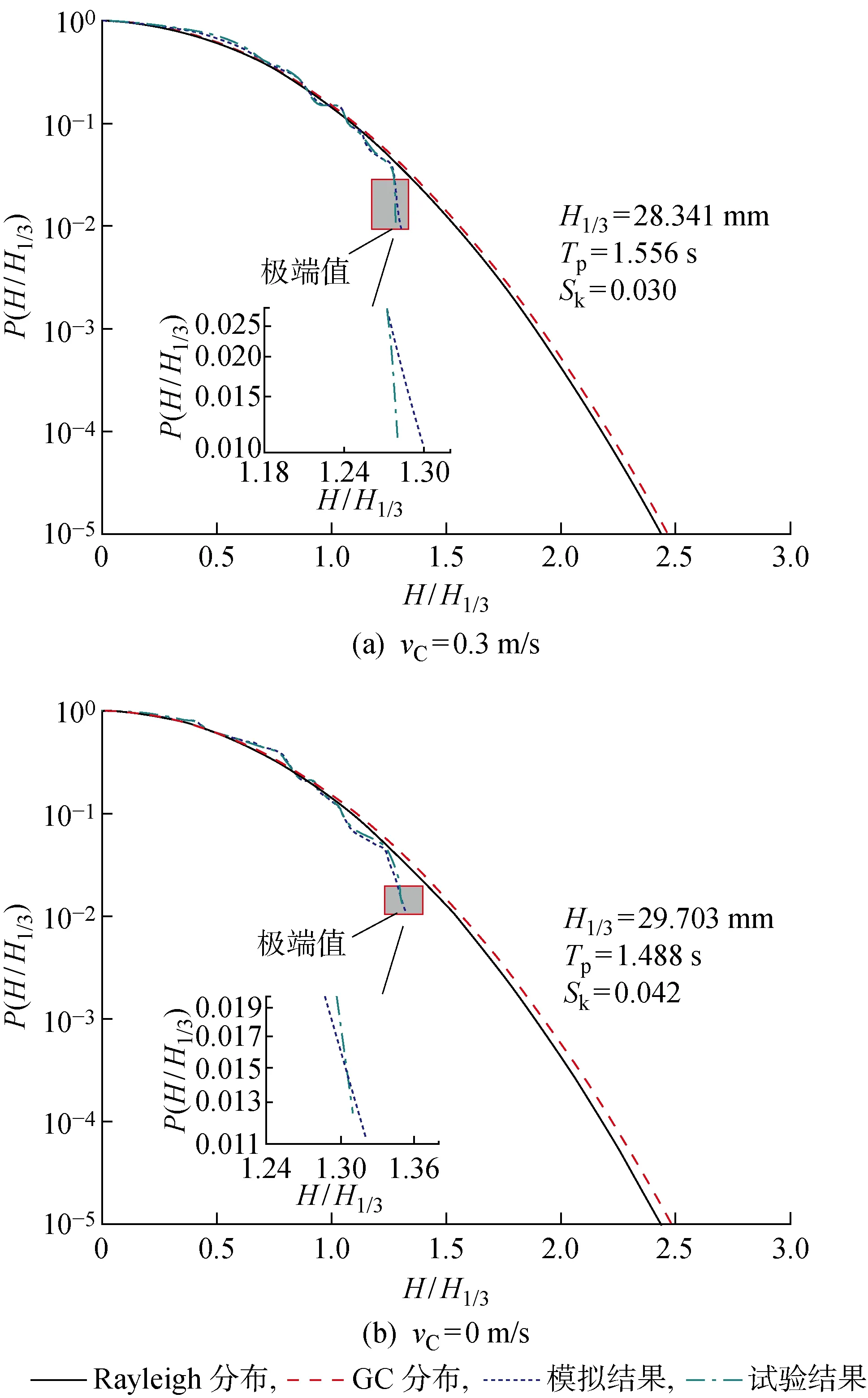
圖4 不同流速下波浪要素與波高概率分布Fig.4 Wave elements and wave height probability distributions at different current velocities

Bitner-Gregersen等[16]利用非線性波浪理論的高階譜方法(HOSM)研究了無流情況下采樣變異性對Pierson-Moskowitz譜和JONSWAP譜不規則波的偏度和峰度等非線性特征的影響情況.上述偏度值計算結果與文獻[16]的結果對比如圖5所示，其中：波陡ε=σpH1/3/2，σp為譜峰周期Tp對應的波數.由圖5可知，相對小波陡的不規則波對應的偏度較小，文獻[16]的結果中大波陡不規則波則對應著更大的偏度，進行數據分析可得兩者的相關系數為0.996，即偏度與波陡存在明顯的正相關關系.在不考慮采樣變異性時，逆流的存在導致波陡和偏度值變大.在波浪被阻隔前，逆流能夠加劇不規則波的二階非線性.

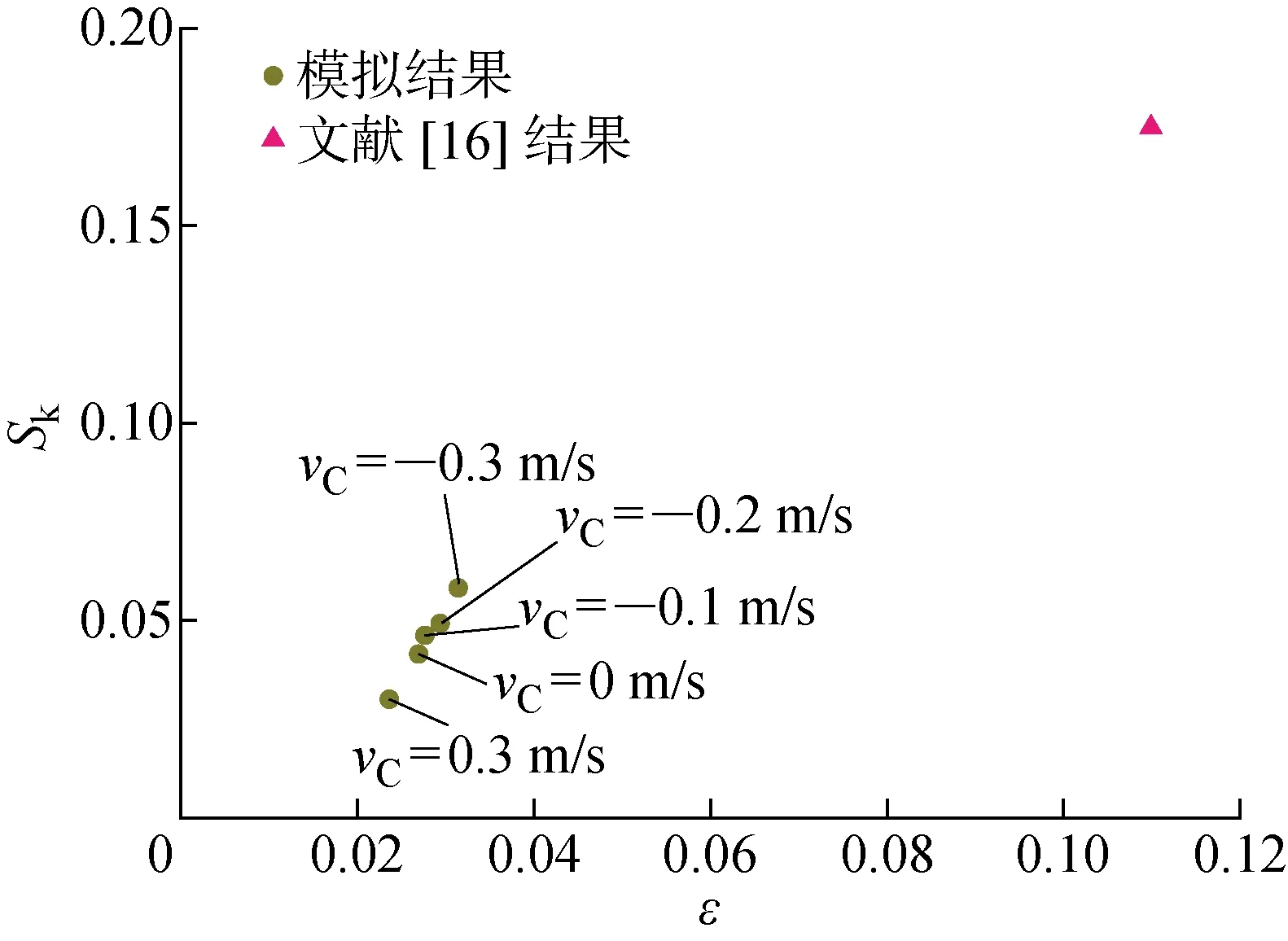
圖5 偏度與波陡的關系Fig.5 Skewness versus wave steepness

當vC=0.3 m/s和vC=0 m/s時，流場渦量隨時間t的變化示意圖如圖6和7所示.其中：Ωj為xj方向的流場渦量；箭頭表示流場旋渦的傳播過程.比較圖6和7可發現，順流流場比無流流場有更大的渦量擴散.結合圖4可知，順流流場渦量增大的同時也導致波浪的有義波高和譜峰頻率有所減小.

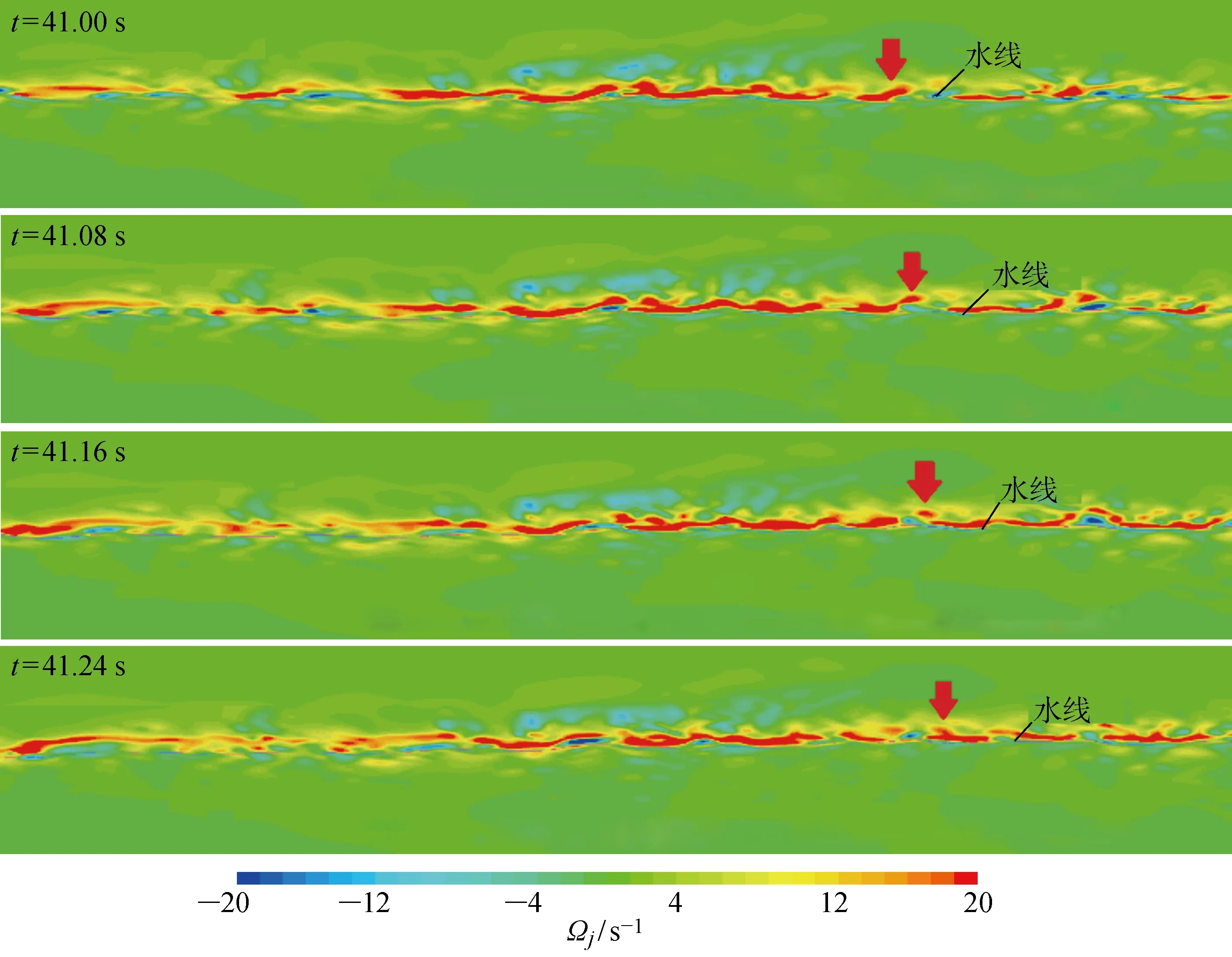
圖6 vC=0.3 m/s時流場渦量示意圖Fig.6 Diagram of vorticity of flow fields at vC=0.3 m/s

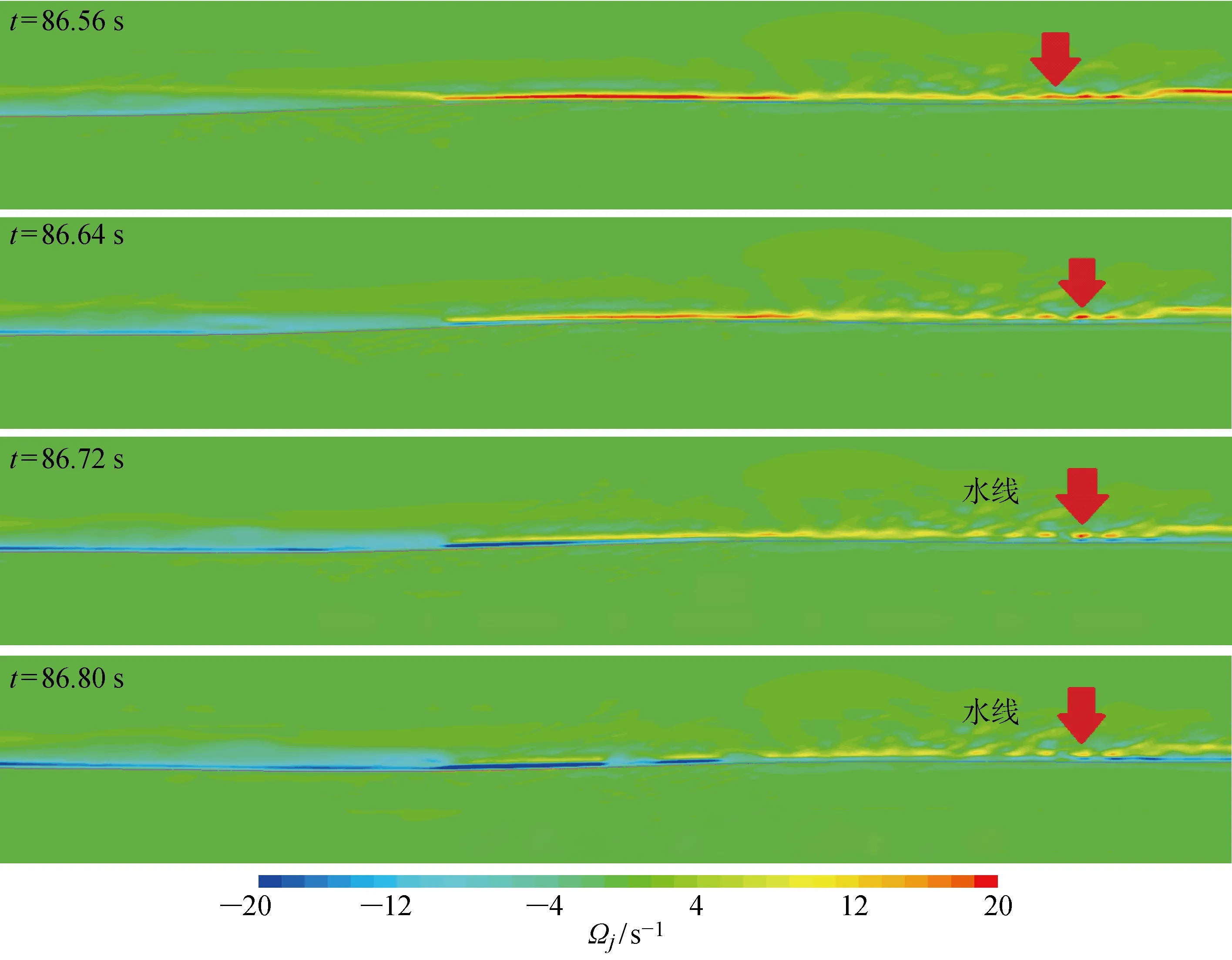
圖7 vC=0 m/s時流場渦量示意圖Fig.7 Diagram of vorticity of flow fields at vC=0 m/s

各個工況最大波峰處波高時歷曲線及其對應的沿z方向分布的水平速度剖面如圖8所示，陰影部分標出了采樣時間內的最大波峰-波谷范圍.由圖8可知，順流時波峰處水平速度大于無流工況且為正值，意味著波峰處水質點向前運動帶動波形向前傳播；順流時不規則波水線面以上的水平速度增長較快，在水線面以下的增長放緩，說明順流作用更顯著地體現在水線面以上的波浪部分.

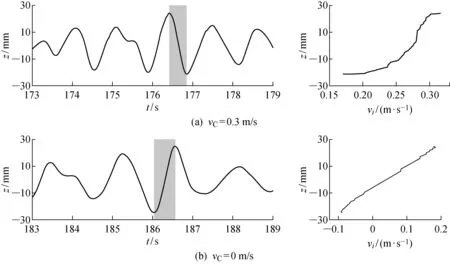
圖8 最大波峰處波高時歷曲線與速度剖面Fig.8 Wave elevations and velocity profiles at the largest crest

波浪能量譜能揭示均勻流對不規則波能量特性的影響規律，順流、無流及逆流情況下不規則波能量譜的數值結果如圖9所示.由圖9(a)可知，順流時不規則波能量譜峰值最小，無流次之，逆流最大，這體現了逆流能量的輸入.由圖9(b)可知，隨著逆流流速的增大，譜峰圓頻率不斷增大，部分能量從低頻向高頻轉移，能量譜譜峰逐漸向高頻區域移動.這也符合研究人員得出的水流對不規則波影響的結論[17-18].

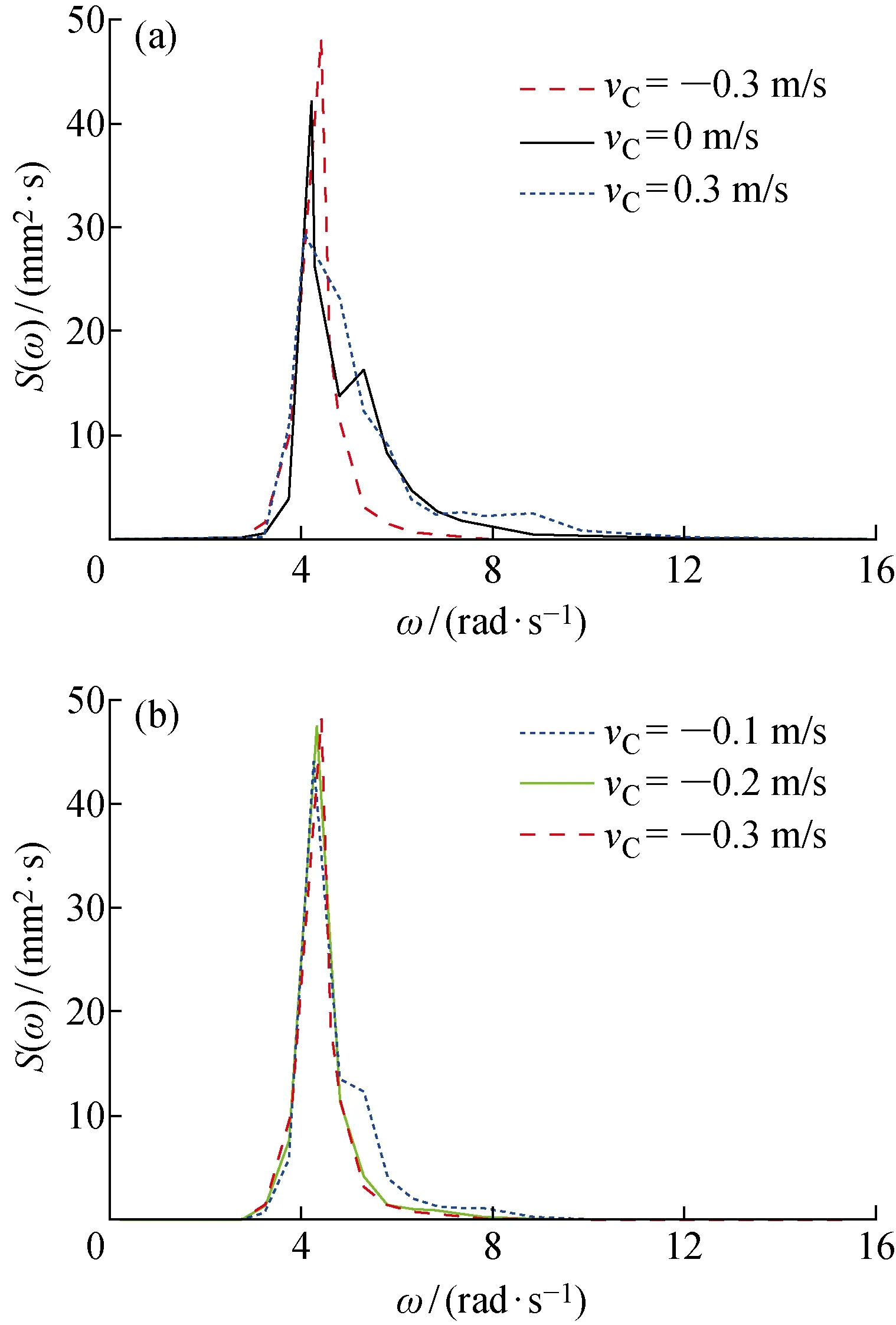
圖9 不同流速下不規則波能量譜對比Fig.9 Comparison of irregular wave energy spectrums at different current velocities

3.2 不確定度分析

在試驗和數值模擬的基礎上，依照國際船模拖曳水池會議(ITTC)推薦的規程對不規則波與順流相互作用的數值模擬結果進行不確定度分析.不確定度分析主要包括兩個方面：驗證與確認.驗證是評估數值的不確定性，本質是分析“是否正確的求解方程”.確認則是評估模型的不確定度，實質是分析“是否求解了正確的方程”.其中，驗證主要包括數值解的多重收斂研究，包括網格收斂性、空間收斂性、時間收斂性、迭代次數和敏感參數收斂性等研究.不規則波與流相互作用屬于非穩態問題，數值模擬中網格尺寸和時間步長大小引起的誤差遠大于迭代步數等其他參數導致的誤差，因此將這兩個參數作為主要影響因素進行分析.

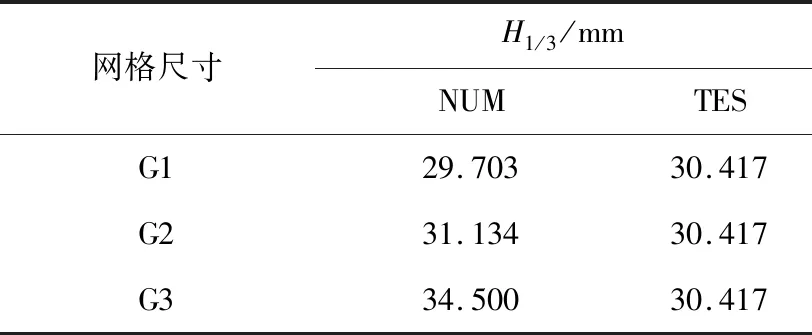
表2 3套網格下的有義波高值Tab.2 Results of significant wave height of three sets of grid sizes

從表2可以計算出相鄰網格G1和G2、G2和G3有義波高模擬值之差的平均L2范數βG21與βG32:

‖βG21‖2=‖HG2-HG1‖2

(7)

‖βG32‖2=‖HG3-HG2‖2

(8)

式中：HGl(l=1,2,3)分別為G1、G2和G3的有義波高數值模擬結果.全局收斂因子RG定義為

〈RG〉=‖βG21‖2/‖βG32‖2=0.425

(9)

實際應用中〈RG〉恒為非負值，網格參數收斂情況可分為兩種：① 單調收斂，0<〈RG〉<1；② 發散，〈RG〉>1.

(10)

(11)

網格修正因子CG為

(12)

式中：網格尺寸趨于0，CG接近1時，首項準確度極限階數估計值AG,est=2.

當|1-CG|<0.125時，網格尺寸引起的數值模擬不確定度UG為

(13)

當|1-CG|≥0.125時，網格尺寸引起的數值模擬不確定度為

(14)

因此，工況1網格尺寸引起的數值模擬不確定度UG=5.93%H1/3,F1，H1/3,F1為F1測得的有義波高試驗值.

(15)

同理，進行時間步長收斂性分析前，先獲得不同時間步長對應的x=4 m自由液面處的波高時歷曲線、有義波高和平均周期，其中有義波高模擬值與試驗值如表3所示.

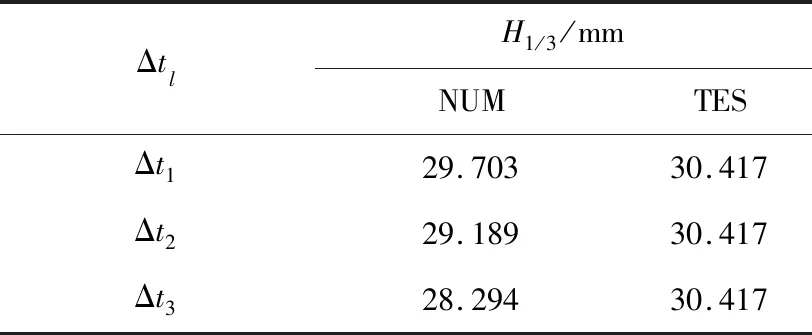
表3 3套時間步長下的有義波高值Tab.3 Results of significant wave height of three sets of time step sizes

依據前文的網格收斂性分析，將與網格尺寸相關的參數修改為與時間步長相關的參數，對時間步長進行收斂性分析，所獲得的時間步長引起的數值模擬不確定度UT為

3.47%H1/3,F1

(16)

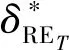
(17)

數值模擬不確定度USN為

(18)

(19)

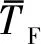
由表4可知，在有義波高的驗證過程中當vC=0 m/s及vC=0.3 m/s時，網格尺寸不確定度均大于時間步長不確定度，可見有義波高對網格尺寸的大小更為敏感.vC=0 m/s時的時間步長不確定度明顯大于vC=0.3 m/s時的時間步長不確定度，說明順流降低了有義波高模擬結果對時間步長的依賴程度.由表5可知，平均周期驗證過程中當vC=0 m/s及vC=0.3 m/s時，時間步長不確定度均大于網格不確定度，可見平均周期對于時間步長的大小更為敏感.因此，在研究順流中不規則波的平均周期時，在計算資源有限的情況下應盡量滿足時間步長的精度要求.順流時網格及時間步長的不確定度均大于無流時的計算結果，說明順流加劇了平均周期模擬結果對網格及時間步長的依賴程度.

在表4中，有義波高在F1下的網格不確定度接近6%，數值模擬不確定度達到6.87%，這是由于網格G3較粗糙，導致的誤差較大.為了改善網格的迭代收斂性，可布置更加精細的網格進行計算.

表4 有義波高模擬結果的驗證Tab.4 Verification of simulation results of significant wave height

表5 平均周期模擬結果的驗證Tab.5 Verification of simulation results of average period

3.2.2確認 對數值模擬結果進行確認，同樣以F1的有義波高為例，確認不確定度UV為

(20)

式中：UD為有義波高試驗值的不確定度，此處取為2.5%H1/3,F1.模擬值與試驗值比較誤差的二范數E為

E=‖H1/3,F1-H1/3,N1‖2=2.35%H1/3,F1

(21)

式中：H1/3,N1為工況1數值模擬的有義波高值.可見UV>E，由F1數值模擬得到的有義波高在7.32%H1/3,F1的水平上實現確認.

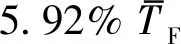
表6 有義波高模擬結果的確認Tab.6 Validation of simulation results of significant wave height

表7 平均周期模擬結果的確認Tab.7 Validation of simulation results of average period

綜上，本文基于RANS方程和VOF方法建立的不規則波與順流相互作用數值模型在求解不規則波有義波高和平均周期時具有可靠性.

4 結論

(1) 順流及無流時不規則波的波高概率分布符合Rayleigh分布；與無流情況相比，順流時不規則波的譜峰周期增加，有義波高和偏度值則減小，可能的極端波高也有所減小.

(2) 順流時波峰處水質點水平速度大于無流時的計算結果，并且順流流場比無流流場有更大的渦量擴散.

(3) 不規則波與順流相互作用時，有義波高對網格尺寸更加敏感，順流能降低有義波高對時間步長的依賴程度；平均周期則更依賴于時間步長，順流作用下平均周期對網格及時間步長的依賴程度加劇，考慮順流時的不規則波平均周期時，在計算資源有限的情況下應盡量滿足時間步長的精度要求.

(4) 順流及無流時不規則波有義波高和平均周期計算結果皆得到確認，不規則波與順流相互作用的數值模型具有可靠性.

由于水槽造波系統設備的局限性，本文研究未能開展逆流中的實驗驗證，今后擬研發循環水槽逆流中造波(包括消波)技術，開展逆流與不規則波相互作用的不確定度分析的相關試驗與數值研究.

致謝感謝上海交通大學循環水槽實驗室的支持及代燚、王飛老師對試驗的幫助.