基于支持向量機的辦公建筑逐時能耗預測

肖 冉, 魏子清, 翟曉強

(上海交通大學 制冷與低溫工程研究所,上海 200240)

近年來,我國建筑能耗保持上升趨勢,全國建筑總能耗已達到8.99億噸標準煤,公共建筑能耗占比為38.53%[1].公共建筑的節能減排主要通過節能改造和優化建筑管理實現.建筑能耗預測是建筑管理的重要一環,為能源的供需匹配和建筑能源系統智能控制提供了參考[2-3].當前的建筑預測模型主要分為兩類,一類是基于熱力學計算的物理模型,另一類為基于機器學習的數據模型[4].相較于基于仿真計算的物理模型,數據模型具有預測精度高、計算速度快的優勢,在歷史數據充足的情況下多采用數據模型[5].數據模型使用機器學習算法學習大量歷史數據中的規律、逼近影響因素和建筑能耗間的函數關系[6].能耗預測領域常用算法包括隨機森林(RF)、人工神經網絡(ANN)及支持向量機(SVM)等[7].

建筑運行能耗受到氣象條件和人員使用等多參數的影響,同時存在隨機事件的擾動,因此能耗變化規律有著較強的非線性和不確定性.機器學習算法中,SVM算法對建筑能耗非線性特性有較好的擬合能力[8]且運算量較小,因此廣泛應用在建筑能耗預測領域[9].此外，當前多數預測模型僅給出能耗預測值,模型預測誤差與建筑運行不確定性無法區分.僅使用單一的預測值難以全面反映建筑運行狀態，而使用置信區間可以處理建筑能耗預測的不確定性問題[10].

針對上述問題,本文采用實際辦公建筑的歷史運行能耗數據和當地氣象數據,基于SVM算法建立了建筑逐時總能耗的預測模型.通過單變量模型驗證模型輸入變量,使用網格搜索優化模型超參數,從而提高了模型的預測精度.在高精度預測模型對運行非線性規律進行解釋的基礎上,結合擬合誤差的置信區間,使用預測區間描述建筑運行的不確定性，最終實現對辦公建筑能耗變化趨勢及波動范圍的準確預測.

1 SVM算法與網格搜索優化

1.1 SVM算法原理

SVM是一種強大的有監督的機器學習方法，可以有效處理非線性的分類和回歸問題,并且能高效地處理高維空間問題[11].使用SVM算法處理回歸問題時,算法根據訓練集數據,逼近變量間的關系函數:

f(x)=〈w,φ(x)〉+b

(1)

式中:x為輸入向量;w為權值系數;φ(x)為映射函數;b為偏置.

SVM算法在逼近函數關系過程中,通過最小化權值系數平方和來保證函數關系的平滑；同時容許小于ε的誤差,以提高模型的泛化性能[12].因此通過求解下述二次凸規劃問題確定w和b[13]:

(2)

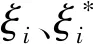
引入隱式的核函數替代顯式的φ(x),將非線性問題映射到高維空間,從而構造出線性可分離平面并求解[13].為解決建筑能耗與影響因子間的非線性關聯,選擇常用于處理非線性問題的核函數為徑向基函數(RBF):

(3)

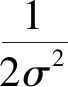
C、ε及γ參數被稱為模型超參數,其在模型訓練過程中為常數,調節模型超參數可以改變模型性能.

1.2 模型性能評價及網格搜索優化

為對比不同模型間的預測性能,量化評價模型的預測誤差,利用平均絕對百分比誤差(MAPE)和決定系數(R2)作為模型誤差評價指標.其中,MAPE反映誤差與實際值的相對大小.R2為1減去模型未解釋的變量方差與總方差之比,其越接近1則說明模型性能越好.MAPE與R2由分別由下式計算:

(4)

(5)

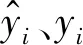
不斷調節模型超參數來獲得更好的模型評價指標,從而優化模型性能.調節超參數的方法有隨機搜索法、網格搜索法、遺傳算法及粒子群算法等.其中,隨機搜索法穩定性較差;而遺傳算法和粒子群算法運算時間過長;網格搜索法在控制計算量的同時,可以搜索較廣的參數空間.故選取網格搜索法作為超參數調節的方法.網格搜索法通過計算指定的參數網格中所有節點,最終確定最優參數組合.本文模型使用Scikit-learn算法庫提供的SVM算法包,該算法包通過對標準數據集的測試設定了默認參數,將其默認參數C=1、γ=0.036及ε=0.1作為網格的基準值,在其附近建立網格[11].使用10為底的指數網格提升搜索范圍,經過在本文數據集上的初步測試后,選擇模型可以正常工作的參數范圍作進一步優化.各節點的參數設定值分別來自如下集合:C∈{0.01,0.1,1,10,100}、γ∈{0.001,0.01,0.1,1,10}及ε∈{0.001,0.01,0.1,1,10},參數節點交叉組成5×5×5的網格.通過交叉驗證計算每個參數組下的模型性能,訓練數據被隨機兩等分,使用其中一半數據訓練模型,另一半數據用于驗證模型性能.為提升模型在數據上整體的擬合能力,以最大化R2為目標進行優化.

1.3 建模預測流程

辦公建筑能耗預測主要內容為建立模型與輸出預測結果,圖1所示為基于SVM的建筑能耗預測流程.建立模型的步驟包含準備數據集與訓練模型.數據集為建筑的歷史能耗數據和運行信息.對數據進行預處理以適用于模型.根據數據的類型,數據被分為輸入變量和輸出變量.按照時間節點,數據集被劃分為訓練集和測試集.算法訓練過程中,先由網格搜索算法提供模型超參數,之后根據訓練集數據,由SVM算法求解權值系數.由網格搜索優化確定最優模型超參數后,使用全部訓練集數據重新訓練得到最終模型.根據測試集輸入,模型計算對應預測值,對照測試集真實能耗值計算模型性能指標.最后結合模型擬合誤差,輸出辦公建筑能耗的預測區間.

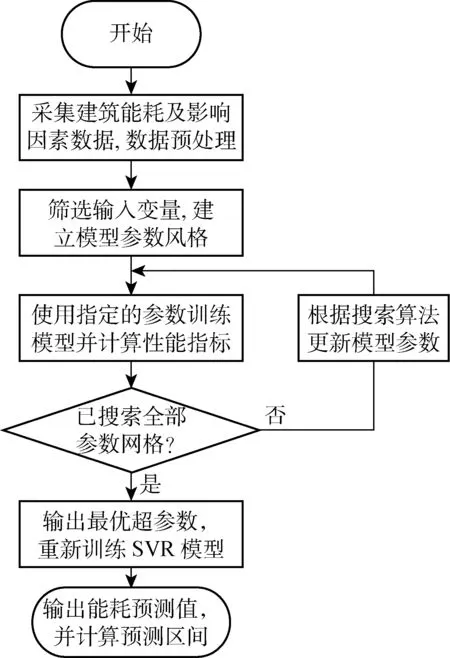
圖1 基于SVM的建筑能耗預測流程Fig.1 Flowchart of building energy consumption forecast based on SVM

2 模型預測情景

2.1 辦公樓案例數據

采用上海市某辦公建筑實際運行過程中能耗監測系統采集的逐時總能耗數據.數據集包含2017～2018年內共 15 360 個數據點.建筑總能耗E隨時間T的逐時變化如圖2所示.辦公建筑能耗有如下特點:① 季節性,可分為供暖季節、過渡季節及供冷季節;② 較強的周期性,與辦公人員的作息規律一致.

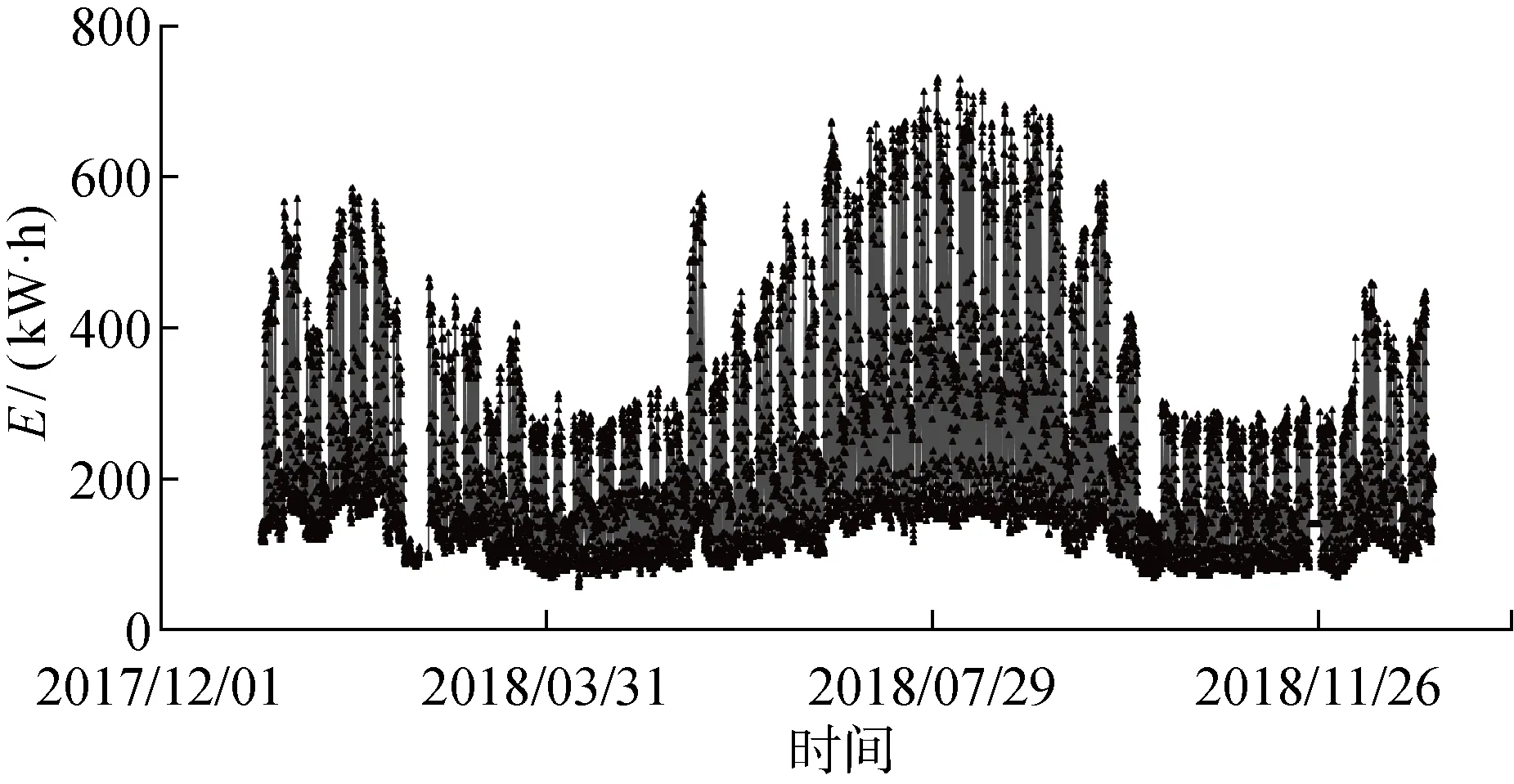
圖2 2018年辦公建筑逐時總能耗曲線Fig.2 Curves of hourly energy consumption of office building in 2018

建立預測模型還需要對應的影響因素數據,包括室外氣象參數和建筑運行信息.室外氣象參數由氣象監測站數據取得[14],為逐時數據,包括室外溫濕度、風速及降雨量等.辦公建筑運行的規律性較強,因此將建筑運行特征、歷史能耗數據等與建筑運行規律相關的數據作為運行信息輸入.

訓練模型前進行數據清洗和數據歸一化.建筑能耗數據常見異常值有負值和過大值兩類,針對本文數據集采用[0,1 000]的區間篩選并剔除異常數據,之后通過線性插值對缺失點進行補全.數據歸一化對所有數據進行比例縮放,映射到[0,1]區間.數據歸一化保證了模型的計算穩定性,最終模型輸出值由逆向區間縮放得到預測值.

2.2 模型輸入變量

本案例的預測情景為不同季節條件下預測辦公建筑未來一段時間的能耗曲線.為使數據模型適用于辦公樓的能耗預測情景,需要確定合適的模型輸入變量.模型輸入變量為建筑能耗的影響因素,包括氣象參數(室外氣溫,室外相對濕度,風速)、運行規律變量(當前時刻,工作日與否)及時間序列參數.

運行規律中,對當前時刻變量進行One-hot編碼,將數值型的時刻轉化為類別變量.時間序列參數來自建筑歷史能耗值序列.通過自相關函數(ACF)篩選該參數,ACF值反映了該序列與其自身在N個小時前的序列的相關性[15].對辦公樓全年能耗數據計算ACF值,如圖3所示.在盡可能減少輸入的前提下,可選擇1 h、24 h前能耗值作為輸入變量.

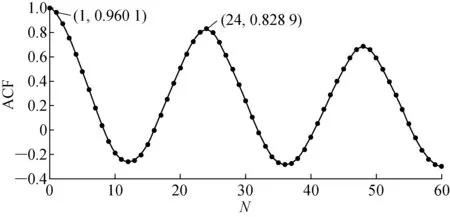
圖3 辦公建筑能耗序列自相關函數值Fig.3 Autocorrelation function for energy consumption sequence of office building

鑒于建筑能耗的非線性特性,使用模型檢驗法選擇變量.使用單變量模型擬合數據,計算模型在訓練集上的性能指標.使用默認參數的SVM模型,在夏季能耗數據(7～8月)上,對比各單變量模型的R2,反映該變量與模型輸出的相關性,結果如表1所示.

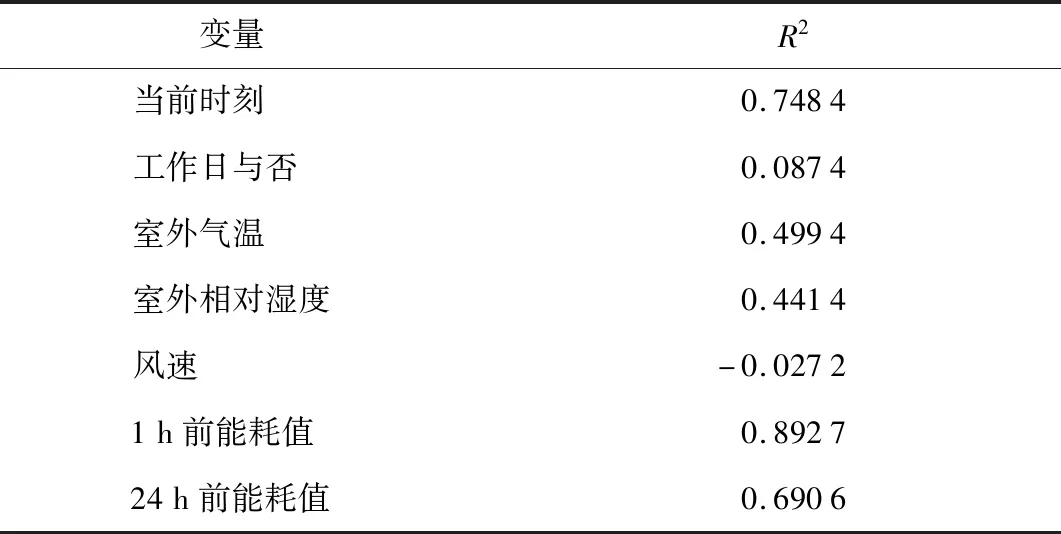
表1 單變量模型檢驗的R2Tab.1 R2 of univariate model test

實際應用場景中,為獲取未來一整天的能耗預測曲線,不使用1 h前能耗值作為輸入.工作日與否變量在逐時預測里相關性略低,但仍是反映逐周能耗變化規律的重要變量.最終確定的模型輸入變量有當前時刻、工作日與否、室外氣溫、室外相對濕度及24 h前能耗值.

3 模型檢驗及預測區間

分別在供暖季節、過渡季節和供冷季節進行建模預測,并檢驗模型預測性能.受季節條件限制,使用不同季節中前兩個月數據作為訓練集.為減少驗證結果的偶然性,連續預測接下來一周的逐時能耗曲線.供暖季節訓練集時間為2017年12月～2018年1月,預測2月第1周能耗.過渡季節訓練集為2018年3月～2018年4月,預測5月第1周能耗.供冷季節訓練集時間為2018年7月～2018年8月,預測9月第1周能耗.

3.1 不同季節能耗預測模型

使用訓練集數據訓練模型后,用得到的模型分別計算一次訓練集和測試集,檢驗模型擬合訓練數據和預測未知數據的能力.分別使用默認參數的SVM與網格搜索優化的SVM模型(GS-SVM)訓練及檢驗,結果如表2所示.

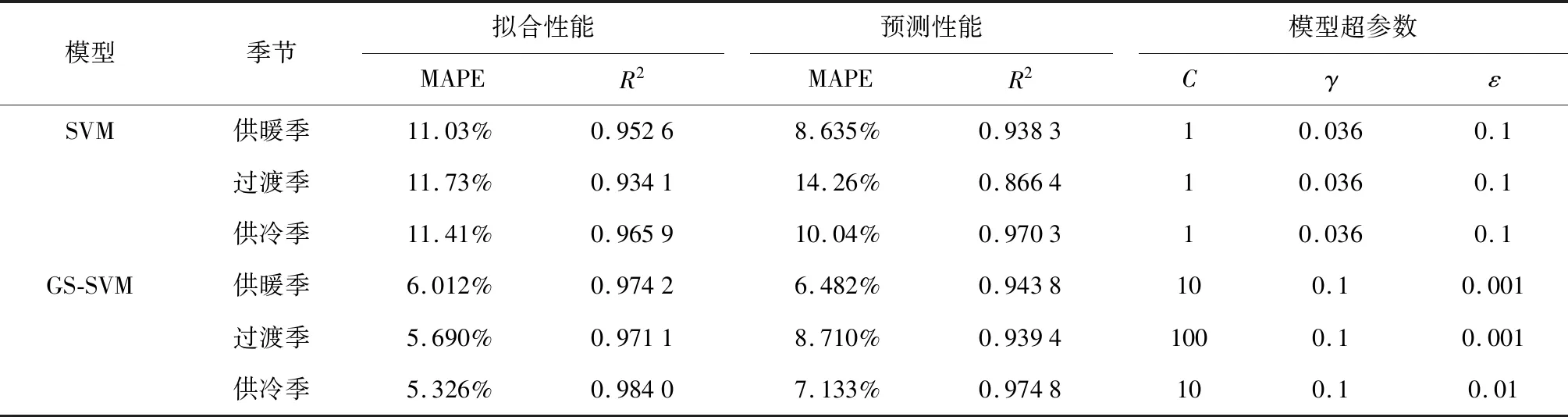
表2 不同季節下的模型性能對比Tab.2 Comparison of model performance in different seasons

所有季節條件下,GS-SVM的模型擬合及預測的性能指標均優于默認參數下的SVM模型,說明網格搜索法優化模型超參數有效提升了模型性能.模型存在季節間的差異,供暖季節和供冷季節的預測性能指標略優于過渡季節.GS-SVM在不同季節預測時,均需要重新搜索最優的模型超參數.使用算術平均代表模型全年整體性能.SVM的整體MAPE為11.0%,整體R2為0.925.GS-SVM的整體MAPE為7.56%,降低31.3%;整體R2為0.953,模型未解釋方差比例(1-R2)降低37.3%.說明該預測方法能較好擬合建筑的非線性變化特性.

3.2 基于模型擬合誤差的預測區間

通過GS-SVM模型獲得了高精度的模型預測,還需要對建筑運行的不確定性進行描述,用以表現建筑能耗的變化情況.將GS-SVM模型擬合的誤差e視為滿足獨立同分布條件的隨機變量,采用置信度為(1-α)的置信區間[eα/2,e1-α/2],即數據有(1-α)的概率落入置信區間內,eα/2、e1-α/2分別表示上、下分位點.在模型輸出上疊加置信區間,預測值轉化為預測區間.就預測模型而言,預測區間補充了當前模型未納入的隱藏變量.針對建筑運行,預測區間基于歷史規律,表現了隨機擾動下的建筑能耗正常波動范圍.

辦公建筑最主要的相關變量為當前時刻,因此按各個時刻將誤差分類.將擬合數據中每個時刻的所有誤差值排序,取α=0.1,將排序位于95%和5%的誤差值分別作為上下分位點,形成置信度0.9的誤差置信區間.按小時不同,預測值疊加誤差上下限后,得到辦公樓夏季的總能耗預測區間,以供冷季節為例,結果如圖4所示.

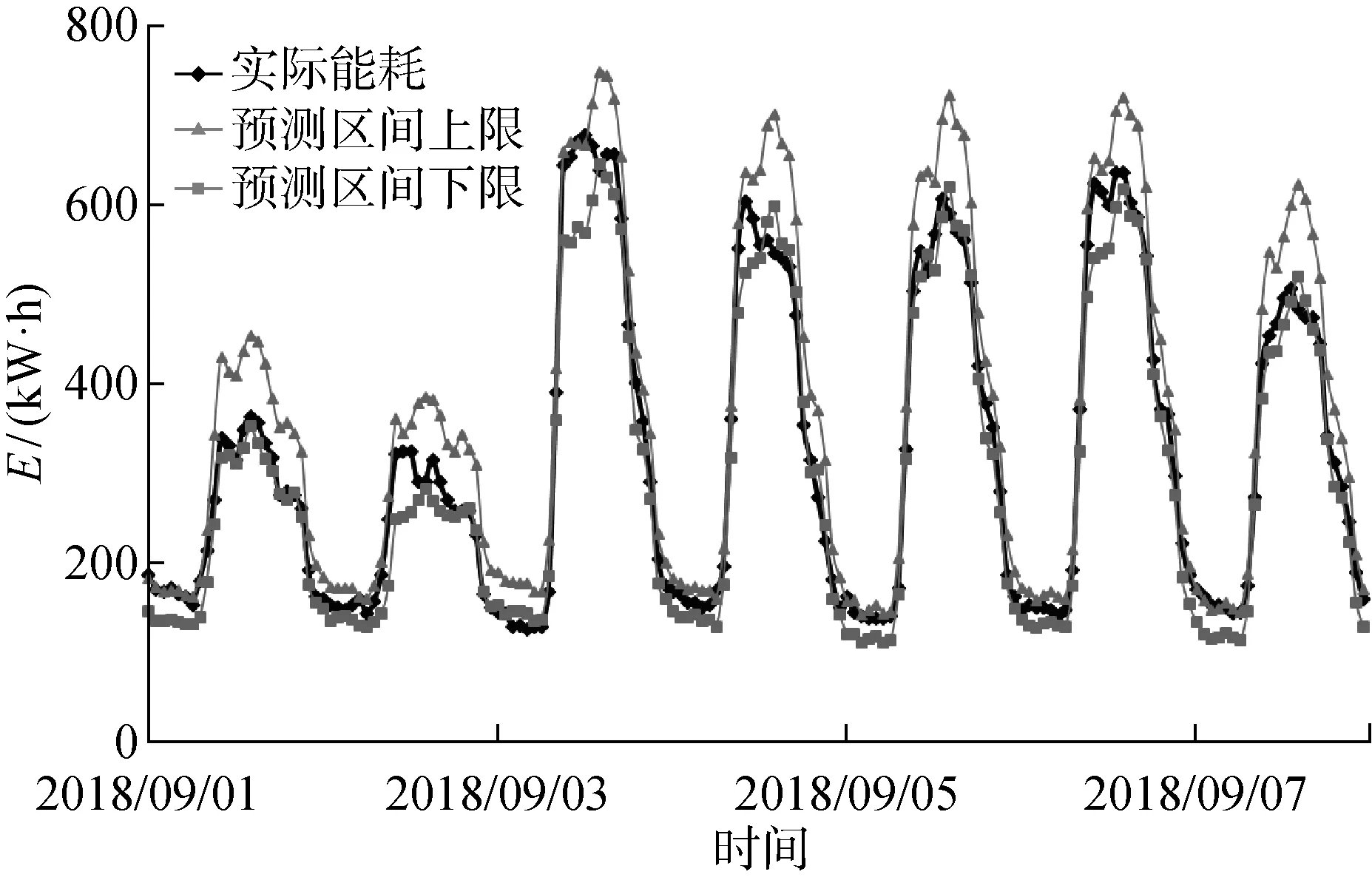
圖4 供冷季節辦公樓總能耗預測區間示意圖Fig.4 Diagram of energy consumption prediction interval for office building in cooling seasons

區間內的能耗值視為已被準確預測,不計算誤差.對區間外的點計算與上下限之間的誤差,得到更新后的MAPE.同時統計實際能耗位于區間內的比例Pin.針對不同季節的模型,結果如表3所示.

表3 預測區間的預測性能Tab.3 Forecast performance of prediction interval

加入預測區間后,MAPE<1.5%,Pin>75%,說明預測區間較好地覆蓋了建筑的能耗變化范圍.使用預測區間的方法可以更全面反映建筑運行狀態.

4 結論

針對建筑運行能耗因非線性及不確定性較強而難以預測的問題,本文提出了一種基于SVM的建筑能耗預測方法,可有效地預測建筑能耗變化趨勢.在辦公樓案例上的驗證結果表明：

(1) 與默認參數的SVM模型相比,GS-SVM模型整體MAPE和1-R2分別降低31.3%與37.3%,模型誤差顯著減小,更好地擬合了建筑能耗的非線性特性;

(2) 使用能耗預測區間替換能耗預測值,各季節中MAPE均減小至1.5%以下,反映了建筑在不確定條件下的能耗波動范圍.本方法在不同季節的測試中預測性能均較優且相互差異小,具備全年不同工況下穩定運行的潛力,可為建筑運行診斷及優化提供參考.