隱蔽空間下超寬帶 TDOA定位算法研究

王佰亮，劉江波

(國家糧食和物資儲備局，北京 100038)

1 概述

隨著國內城市化和機動化的加快，具有節能、快捷和大運量特征的城市軌道交通建設越來越受到眾多城市的關注，軌道交通路網建設進程不斷發展。其中，施工安全是整個軌道交通建設行業的重要問題，特別是隧道等隱蔽空間施工安全問題。隱蔽空間施工環境艱苦惡劣、危險系數高、施工人員多，使得施工建設企業面臨巨大的管理難度。因此，通過新型技術手段實現對隱蔽空間工作人員的準確定位，對保障人員安全、災后急救等尤為重要。

盡管GPS 可以很好的解決室外多數環境中的精確定位問題，但對于各種室內、地下、隧道等特殊場景，GPS 卻無能為力。目前，應用于各種室內、地下、隧道等特殊場景的主流定位技術包括Wi-Fi定位技術、射頻識別技術、Zigbee 定位技術、UWB 定位技術等[1]。UWB 定位技術由于定位精度高[2-3]，部署方便，在隱蔽空間定位中得到了廣泛的應用。各種定位系統中常用的位置解算方法有最小二乘算法、泰勒級數算法、Chan 算法等[4]。這些算法應用于隱蔽空間定位的不足之處在于：LS 算法雖然運算簡單快速，但求出的卻是次優解；Taylor算法需要一個與實際位置接近的初始值，若初始值誤差大將導致算法不收斂，并且Taylor 算法運算量較大[5]；Chan 算法和LS 一樣，雖然計算快捷，但是在非視距(NLOS) 環境下定位性能顯著下降[6]。BP 神經網絡有強大非線性映射能力，近年來廣泛運用于各種定位系統，在提高定位精度上有較大的優勢[7-9]，但也存在收斂速度的問題。為此，研究了一種結合最小二乘位置求解方法（LS）的BP 神經網絡定位算法，在提高BP 收斂速度的同時提高定位精度。

2 最小二乘融合BP神經網絡定位算法

2.1 融合定位思路

最小二乘融合BP 神經網絡定位算法的基本思路是：利用測量得到的TDOA 值和已知的基站坐標，采用LS 算法進行位置計算，獲得一個與實際位置接近的待測節點位置的粗估計；然后根據待測節點初始估計位置坐標及基站坐標，進行TDOA 測量值重構；運用重構TDOA 及基站信息進行BP 神經網絡訓練及位置解算，優化LS 計算結果，從而獲得最終定位結果。具體過程如圖1 所示。

2.2 最小二乘位置估計算法

假設參與定位的基站坐標為,待測節點坐標為(xi，yi)，i=1，2...N。基站與待測節點間的距離用(x，y)來表示。則：

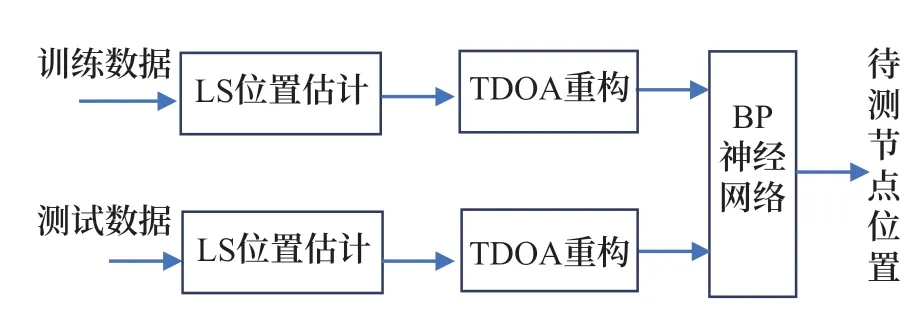
圖1 最小二乘融合BP神經網絡定位思路Fig.1 The scheme combing least square and BP neural network

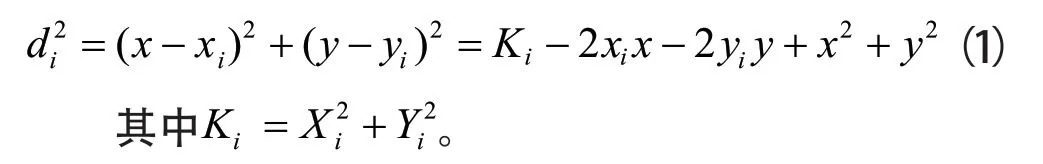
令di，1表示待測節點到基站i與基站1 的距離差。則

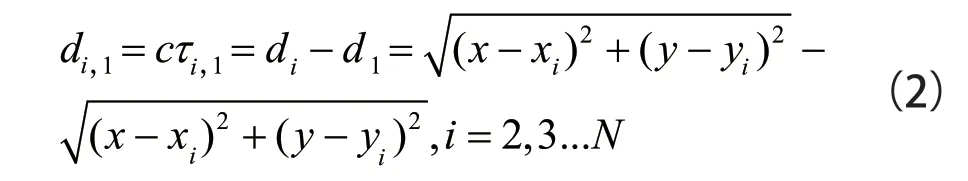
其中c為電波傳播速度，τi，1為TDOA 測量值。對該非線性方程組進行線性化處理，得到

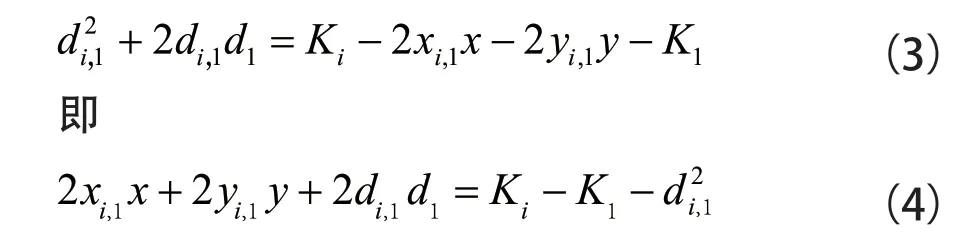
式中xi，1=xi-x1，yi，1=yi-y1。

將x，y，d1看成未知數，公式（4）寫成矩陣的形式為

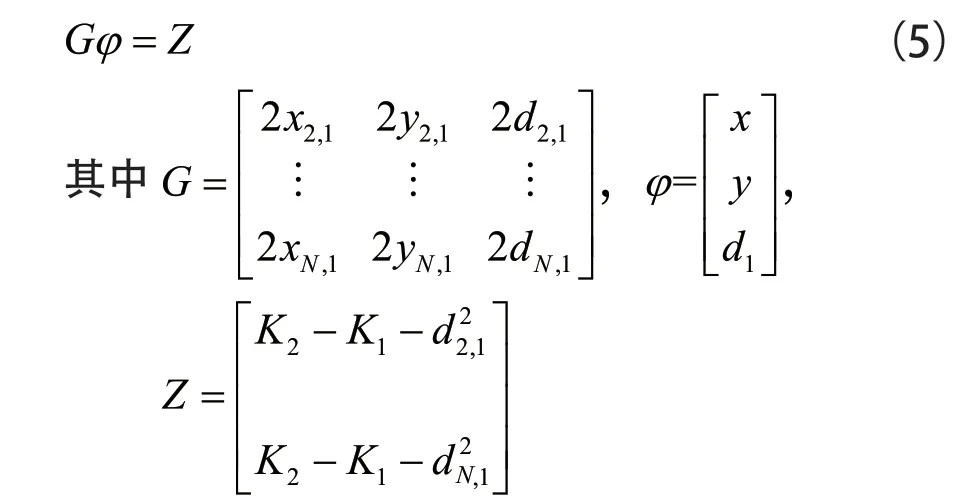
利用最小二乘法求解（5）式得

其中x,y即為待測節點估計位置。利用該估計結果，根據公式（2）即可進行TDOA 重構。

2.3 BP神經網絡位置解算原理

BP 神經網絡位置解算利用重構TDOA 進行網絡訓練，訓練好的網絡將用于對測試數據的位置解算。一般來說，BP 神經網絡是一個多層網絡，包括輸入層、輸出層和隱含層，其中隱含層可以為一層或多層。由于定位模型復雜度不高，經過實測數據進行驗證分析，選取單隱層BP 神經網絡對待測節點進行位置估計，其結構如圖2 所示。

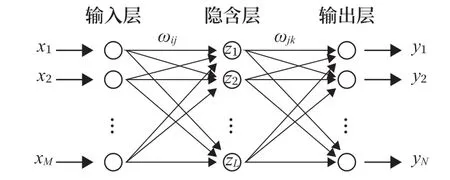
圖2 BP神經網絡結構Fig.2 Structure of BP neural network

BP 神經網絡輸入層由M個神經元構成，M的個數由參與定位的基站數決定。輸入層的輸入是參與定位的基站坐標及重構TDOA，即該TDOA 由LS 算法定位結果修正得到。輸入層的數據結構如表1所示。

輸出層由N（N=2）個神經元構成，對應估計得到的待測節點坐標（x,y）。

隱藏層含有L(L=11)個神經元。隱含層神經元的激活函數選取為tansig 函數，公式為

表1 輸入層數據結構Tab.1 Data structure of input layer

則隱含層的輸出為

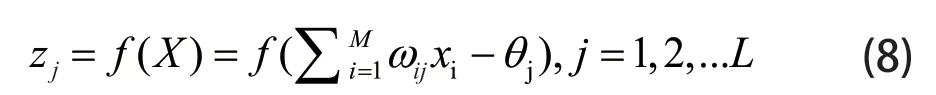
輸出層的激活函數選取為線性purelin 函數。則輸出層的輸出為

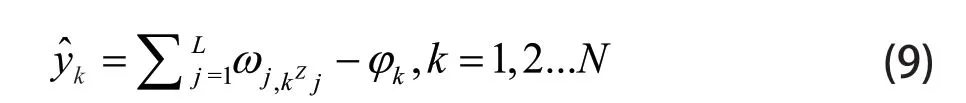
定義誤差輸出函數為

利用反向傳播訓練函數trainlm 函數進行權值更新，更新過程中學習率選取為0.01。

3 性能仿真分析

仿真區域設置為邊長10 m 的二維正方形平面區域。在該區域布置5 個基站，坐標分別為：（0，0）,（0，10），（10，0），（10，10），（5，5）。待測節點在二維平面區域內隨機分布，測量誤差服從高斯分布，非視距誤差服從高斯分布或指數分布。具體仿真過程如圖3 所示。

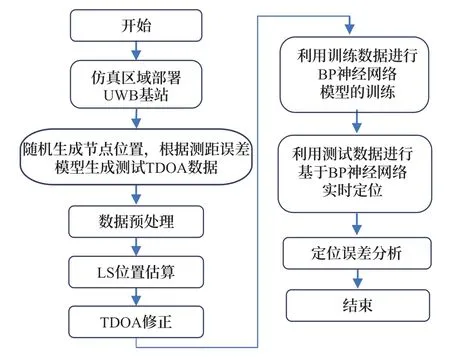
圖3 仿真過程Fig.3 Process of simulation

基站與待測節點間視距傳輸時的仿真結果如圖4、5 所示。視距傳輸時只考慮測量誤差。從圖4、5 中可以看出測量誤差分別服從均值為0，標準差為10 cm 或15 cm 的高斯分布。基站與待測節點間非視距傳輸時的仿真結果如圖6、7 所示。非視距傳輸時除考慮測量誤差外還要考慮非視距誤差。從圖6、7 中可以看出測量誤差都服從均值為0，標準差為10 cm 的高斯分布；如圖6 所示非視距傳播的誤差服從均值為50 cm，標準差為10 cm 的高斯分布。如圖7 所示非視距傳播的誤差服從指數分布，指數分布的均值為tm，tm=Tdαω，其中10 lg(ω)～N(0，σω)，σω=4，T=19 ns，α=0.5。

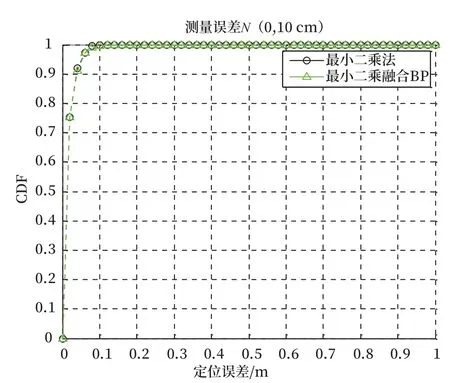
圖4 視距-測量誤差N(0,10 cm)定位誤差Fig.4 LOS-the positioning accuracy for measurement error of N (0,10 cm)

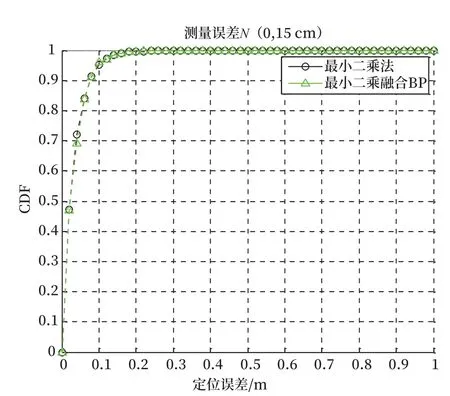
圖5 視距-測量誤差N(0,15 cm)定位誤差Fig.5 LOS-the positioning accuracy for measurement error of N (0,15 cm)

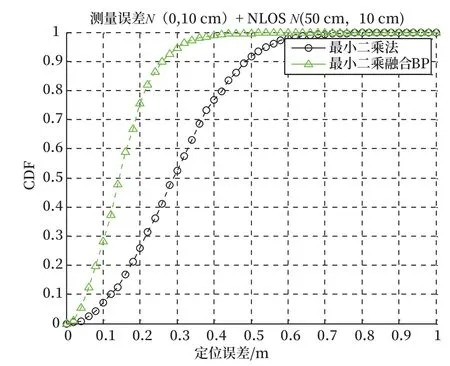
圖6 非視距-NLOS N(50 cm,10 cm)定位誤差Fig.6 NLOS-the positioning accuracy for NLOS N (50 cm,10 cm)

對比最小二乘融合BP 神經網絡的定位方案以及最小二乘法定位方法的定位誤差累積分布函數可知，在視距傳輸情況下，最小二乘融合BP 神經網絡的定位方案與最小二乘法定位方法定位精度相當。但在非視距環境下，最小二乘融合BP 神經網絡的定位方案定位精度明顯高于最小二乘法定位算法。在非視距誤差服從均值為50 cm，標準差為10 cm的情況下，最小二乘融合BP 神經網絡的定位方案中定位誤差小于20 cm 的概率接近80%；而最小二乘法算法定位誤差小于20 cm 的概率只有大概20%。在非視距誤差服從指數分布的情況下，最小二乘融合BP 神經網絡的定位方案中定位誤差小于20 cm 的概率接近100%；而最小二乘法算法定位誤差小于20 cm 的概率只有大概22%。

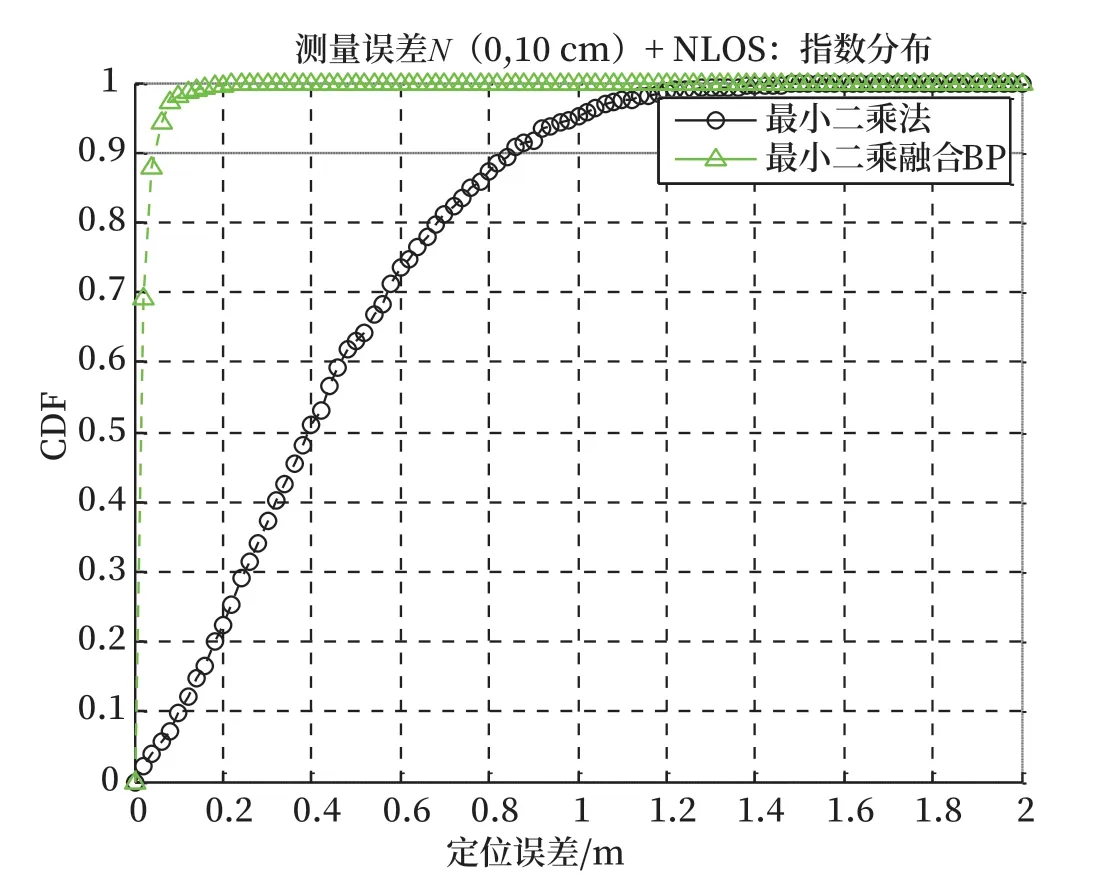
圖7 非視距-NLOS指數分布定位誤差Fig.7 NLOS-the positioning accuracy for exponential distribution of NLOS

其次，4 種情況下各算法的定位誤差最大最小值及均方根誤差如表2 所示。

從表2 可得到和圖4～7 相似的結論。同時可以看出，在非視距情況下，最小二乘融合BP 神經網絡的定位方案中定位誤差均方值遠遠小于最小二乘算法。

4 結束語

研究一種基于TDOA 的最小二乘和BP 神經網絡融合定位算法，該算法在NLOS 環境下利用BP神經網絡進行最小二乘法定位結果優化，降低了NLOS 誤差的影響，明顯提高了定位精度。實驗結果表明，該算法在非視距情況下定位性能遠優于最小二乘法，具有較強的抗 NLOS 誤差能力，能適應不同環境下定位的需求。

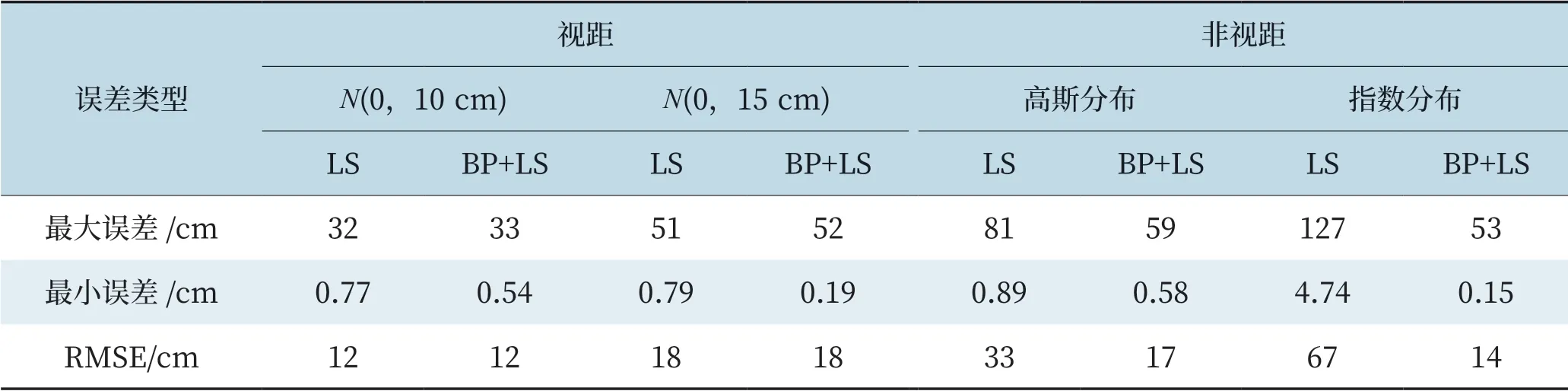
表2 均方根誤差Tab.2 Root mean square error