接觸式輪廓掃描儀系統標定算法*

高 彤 ，陳 鴻 ，張 亮 ，王晉祺

(1.中北大學 電子測試技術重點實驗室 儀器科學與動態測試教育部重點實驗室，山西 太原030051；2.太原科技大學 交通與物流學院，山西 太原030051；3.上海無線電設備研究所，上海201109)

0 引言

現如今檢測技術朝著精密、高效的方向不斷提升，眼鏡的生產和加工也向著高精度、自動化方向發展。 傳統的方法需要定制相應的模板，工序復雜，耗時長，而且精度不高[1]，不滿足工業生產需求。 目前國內外普遍使用鏡片自動磨邊機，它是一種根據輪廓掃描儀所提供的輪廓數據進行自動加工鏡片的設備，實現鏡架凹槽或鏡片輪廓參數的獲取并傳給數控磨邊機從而實現加工全自動。測量輪廓的方式主要分為接觸式測量和非接觸式測量。 接觸式測量利用掃描探針與被測物體接觸，使掃描探針或被測物體旋轉一周，實現對被測物體進行離散的空間點位置的獲取，通過一定的數學計算，完成對所測數據點的分析擬合，最終還原出被測物體的輪廓；非接觸測量有超聲波法以及基于視覺技術的激光三角法、結構光法等[2-4]，但利用光學的測量方式不適用于鏡架凹槽。本文所研究的接觸式探針掃描儀利用低壓力接觸式探針掃描鏡架內凹槽或鏡片邊緣輪廓，其掃描原理就是利用檢測探針接觸被測物體一周的過程中得到旋轉編碼器返回的長度序列以及旋轉平臺的旋轉角度來確定輪廓的坐標信息，編碼器記錄的長度是檢測探針升起位置到被測物體輪廓邊緣點的距離。 實際工程中，由于儀器零部件的安裝不精準，檢測探針的零點與旋轉中心往往不重合，所以需要對得到的數據進行處理才能得到準確的曲線輪廓[5]。 對于此類系統誤差問題，一般做法是對誤差來源進行分析后，需要建立誤差的精準數學模型，提出系統誤差補償或抑制方法[6-9]。 為了解決本文研究的問題，參考文獻[10]提出的方法是對誤差進行了精確建模，建立系統的誤差數學模型，運用最小二乘法的基本原理求解最佳參數[10-12]，但這種方法運算量較大，難以實現在線標定[13]。 本文提出一種利用尺寸已知的正方形標定板，通過測量標定板得到的數據來獲取到系統參數，從而對被測物體的輪廓坐標進行在線標定。 并通過Qt Creator 軟件編程模擬仿真了測量過程驗證了算法的準確性。

1 掃描測量原理及誤差產生原因

應用極坐標系下的構圖原理，如圖1 所示，以滑軌的初始位置為極坐標軸建立坐標系，坐標原點O 為檢測鉤升起的位置，旋轉編碼器記錄由檢測鉤起始點到測量邊緣點P 的長度ρ。 當檢測鉤所在的滑軌每旋轉一個角度Δθ，則有與之相對應的長度序列。 實際測量中，只要能夠獲得被測對象輪廓一周無窮多個位置的坐標(ρ，θ)，即可得到所需輪廓。

圖1 測量原理圖

誤差產生原因：由掃描原理可知，測量點的起始測量位置須是一個定點，這樣得到的數據才準確，而實際測量中由于掃描部件的安裝會有偏差，導致檢測鉤的起始點與旋轉中心點不重合，進而導致檢測鉤起始點在測量過程中是隨旋轉平臺繞旋轉中心而變化的，并非定點。 旋轉中心到檢測鉤所在滑軌存在垂直距離，用這樣得到的數據直接去擬合輪廓不可行，所以在正式測量鏡框前需要對測量系統進行標定。

2 測量系統坐標標定算法

2.1 建立標定模型

建立合適的坐標系對于問題的求解非常關鍵，圖2所示是將被測鏡框固定在卡槽測量鏡框鏡圈。

圖2 鏡框/鏡片掃描儀

為了便于說明測量結果及計算，建立如圖3 所示的測量坐標系，其原點O 為旋轉中心，兩條坐標軸x 軸和y 軸的方向為卡槽的兩組對邊方向。 為了獲取系統參數，這里采用帶有4 個圓角的正方形標定板，將正方形標定板固定在卡槽內，標定板的邊長方向與卡槽的兩種組對邊方向一致，將與第一條被測邊長垂直的坐標軸定為x 軸正方向，按逆時針方向旋轉；將與第二條被測邊長垂直的坐標軸定為y 軸正方向。 Q 為檢測鉤起始點，M 為旋轉中心到檢測鉤所在滑軌的垂心，P 為測量點。將QM 的值設為ΔL，OM 的值設為d。

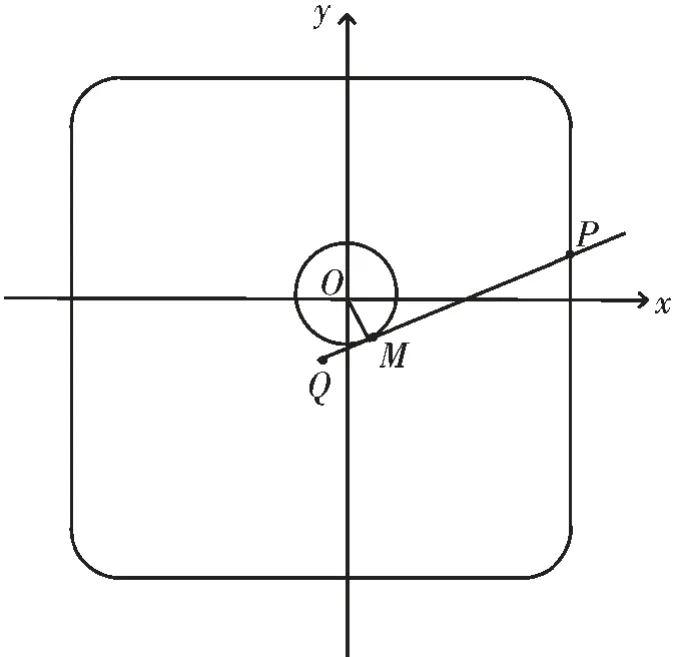
圖3 測量坐標系

2.2 測量系統參數標定

下面選取一種位置情況進行說明，如圖4 所示的參數標定模型中，設選取的一組極小值點的位置如圖中的P0、P2。 測 量 點 是P0位 置 時，設 滑 軌 與x 軸 的 夾 角 為θ0，即∠OP0M0=θ0，其對邊極小測量點為P2，設滑軌與x 軸夾角為θ2，即∠OP2M2=θ2。 在這里不作正負區分，本文規定從x 軸正半軸逆時針旋轉而成的角為正角。

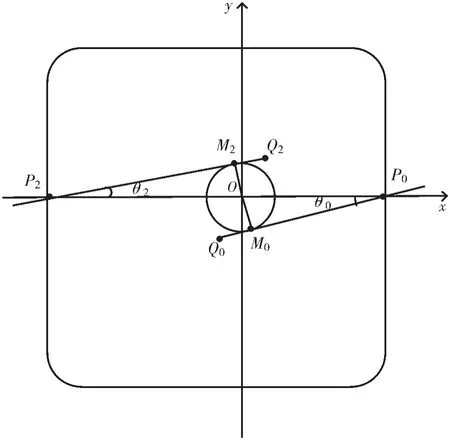
圖4 參數標定模型

已知正方形標定板的邊長L=45 mm，從測量數據可以確定O0P0以及Q2P2的長度分別設為ρ0和ρ2，從測量數據還可以確定滑軌由測量P0點逆時針旋轉到測量P2點所用的旋轉角度Δθ。 則可列出以下方程：

由 于sinθ0和sinθ2均 是 方 程(8)的 解，且 不 相 等，將 測量數據帶入方程(8)解出sinθ0和sinθ2，帶入方程(4)即可解得d。 從ρ0和ρ2的大小關系可以確定該方程的兩個解 與θ0和θ2的 對 應 關 系，若ρ0＞ρ2，則θ0＜θ2，反 之θ0＞θ2，從而確定θ0和θ2的值，將其帶回式(1)或式(2)即可解出QM 的長度ΔL。

得到θ0和θ2的值后，再加上P0、P2在標定模型中的位置確定，即可確定檢測鉤在測量P0、P2點時滑軌與x軸正半軸的夾角。 圖4 這種情況下，在測量P0點時，滑軌與x 軸正半軸的夾角就是θ0。 同理，如果選取的一組數據是P1、P3，得到滑軌在這兩個測量點與y 軸的夾角θ1和θ3，則在測量P1點時，滑軌與x 軸正半軸的夾角為θ1+π/2。

設滑軌在初始位置與x 軸正半軸的夾角為α0，利用滑軌從初始位置逆時針旋轉到測量極小值點的位置時的旋轉角Δα，以及檢測鉤在測量該極小值點時滑軌與x 軸正半軸的夾角即可確定α0。例如測量極小值點是圖4的P0點， 滑軌由初始位置轉到測量P0點位置所用的旋轉角為Δα，則α0=θ0-Δα。

2.3 測量系統坐標標定

獲取到系統參數d、ΔL、滑軌在初始位置與x 軸的夾角α0后，即可對測量點P 的坐標進行標定。 如圖5 坐標標定模型，要確定任意測量點P 的坐標，則需要確定OP與x 軸正半軸的夾角β 以及OP 的長度。 測量P 點時滑軌與x 軸正半軸的夾角α 可由α0和旋轉角Δα 得到，則：

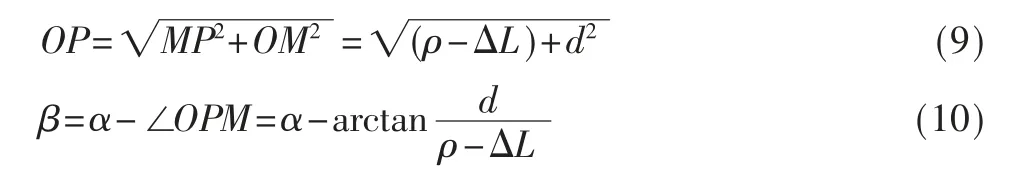
P 點的直角坐標由極坐標到直角坐標系下的轉換即可得P(OPcosβ，OPsinβ)。

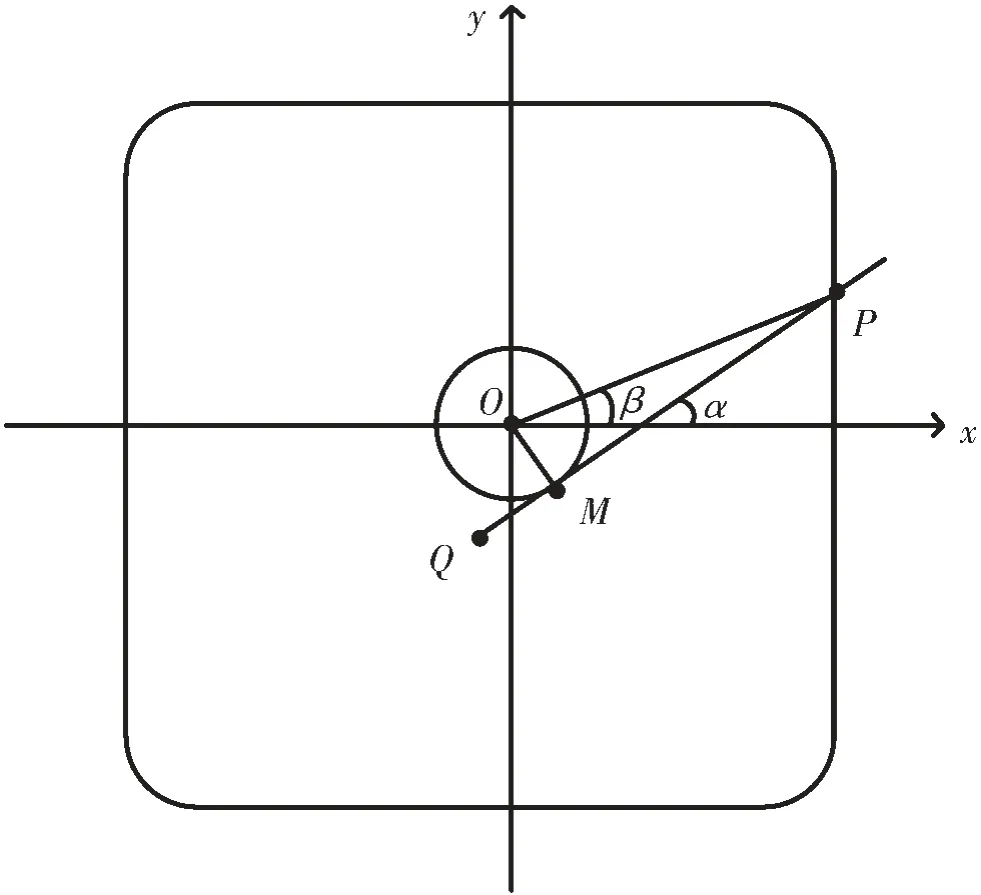
圖5 坐標標定模型

3 測量數據處理

根據上述分析，測量正方形標定板的過程中如果采樣點是連續的才會得到理想極小值點，即邊長與坐標軸交點。而實際工程測量中采樣點是離散選取的。提高采樣點數可以提高取到理想極小值點的概率，本文所研究的接觸式鏡框掃描儀所能達到的角度分辨率最小為0.225°，即旋轉一圈采樣1 600 個點，在此分辨率下根據式(6)給定ρ、θ0后繪制Δθ 和d 的關系圖，如圖6 所示，顯然0.225°的角度分辨率達不到系統要求的0.5 mm 精度。

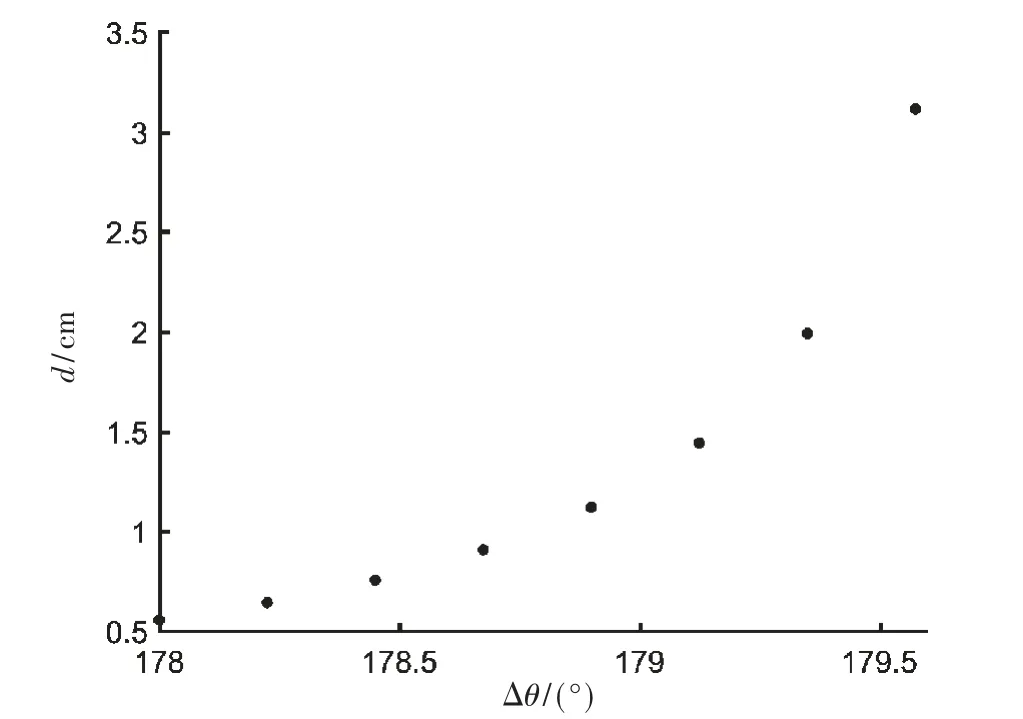
圖6 系統精度說明圖

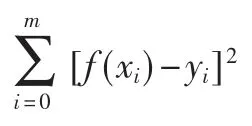
4 模擬仿真實驗

為了驗證標定算法，在給定正方形標定板、旋轉中心與坐標系的相對位置關系后，利用Qt Creator 軟件編程模擬仿真出在給定系統參數d、ΔL、α0下的數據。利用仿真出的數據用標定算法解出系統參數的值并于設定值進行比較，從而驗證算法的準確性。

4.1 測量數據生成

當旋轉中心和標定板的位置關系確定后，測量數據即可確定，與坐標系的位置無關。 這里仍然設旋轉中心為坐標點(0，0)，設旋轉中心到垂心的連線與x 軸正半軸所成夾角為γ，系統的角度分辨率為φ=2π/n(n 為總采樣點數)，γ 的值可由系統角度分辨率和滑軌與x 軸正半軸的初始夾角α0確定，則滑軌運動到任意位置時，旋轉中心到滑軌的垂心坐標為M(dcosγ，dsinγ)。 此時滑軌的斜率k=tan(γ-π/2)，則滑軌所在直線方程確定，利用該直線方程與被測點所在的標定板輪廓曲線或直線方程聯立可得測量點P 的坐標，求出M 點到P 點的距離再加上ΔP 即仿真出測量長度值ρ。

將四角帶有圓弧(半徑為r)的正方形標定板輪廓分為四部分，如圖7 所示，分別為測量點從D0到D1、D1到D2、D2到D3以 及D3到D0。

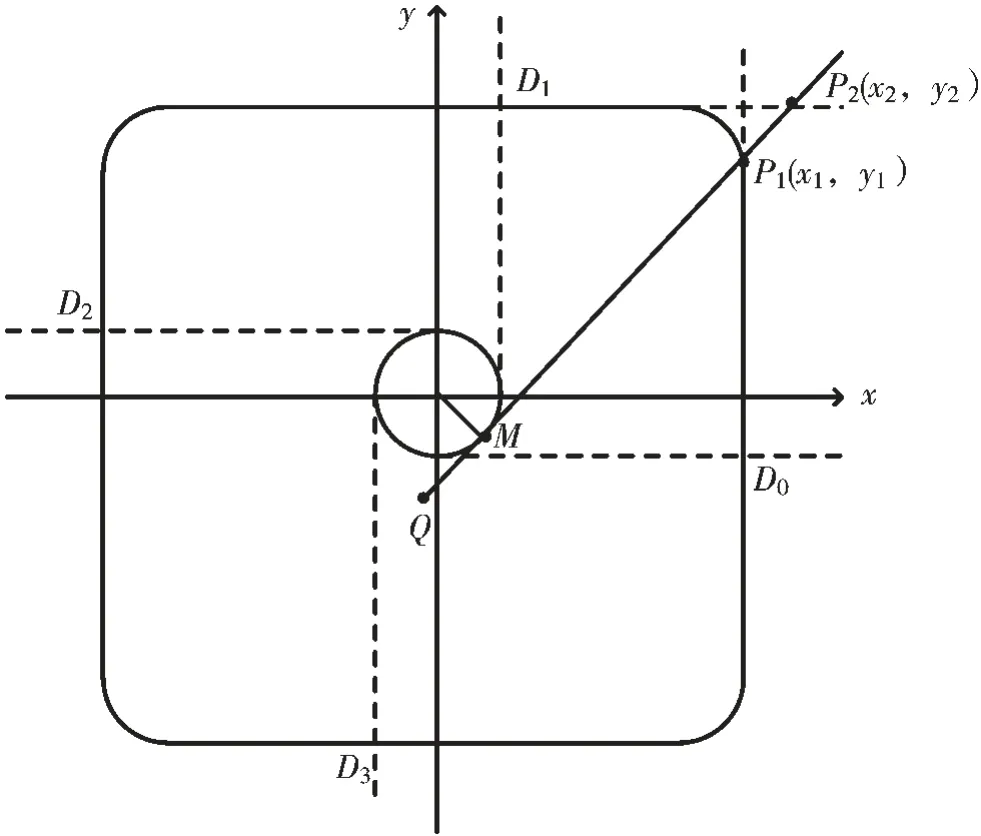
圖7 測量數據生成

當測量點位于D0到D1范圍時，與切線方程聯立的方程分為直線x=x1和y=y2以及圓[x-(x1-r)]2+[y-(y1-r)]2=r2，x1和y2已知。 設與兩條直線聯立解出交點坐標為P1(x1，y1)和P2(x2，y2)，與圓聯立解出兩個交點坐標P3(x3，y3)、P4(x4，y4)，M 點 與 這4 個 交 點 的 距 離 設 為d1、d2、d3、d4。 先比較d1和d2的大小，若d1＜d2，則繼續比較r 與y2-y1的大小，若y2-y1≤r，說明此時測量點位于圓弧上，否則測量點就是D1；若d1＞d2，則繼續比較r 與x1-x2的大小，若x1-x2≤r，說明此時測量點位于圓弧上，否則測量點就是D2。當測量點位于圓弧區段時，比較d3和d4的大小，較大的對應的為此時的測量點。 當滑軌運動到其他區段時測量點的選取過程同理。

4.2 測量數據擬合

模擬出測量數據后，繪制輸出數據曲線波形圖如圖8所示。 對4 個極小值及周圍采樣點進行最小二乘法擬合，即設：f(x)=a2x2+a1x+a0。

對上述矩陣變換求解得到系數矩陣A[14-15]，就得到了擬合曲線。

圖8 輸出數據波形圖

4.2.1 采樣點數目的選取

改變m 的大小得到不同的擬合函數計算出系統參數d，通過比較計算值與設定值的差值選擇合適的m。將用于擬合的采樣點數從5 到100 遞增，得到系統參數d，繪制d 關于采樣點個數的關系折線圖，如圖9 所示。若用于曲線擬合的采樣點數過少，則會導致計算出的系統參數與理想值差距很大，故繼續提高采樣點數的起始設定值，如圖10 所示，當采樣點數選取在40 ～60 范圍內，d 的計算值穩定接近設定值1.00 cm 且符合系統精度要求。

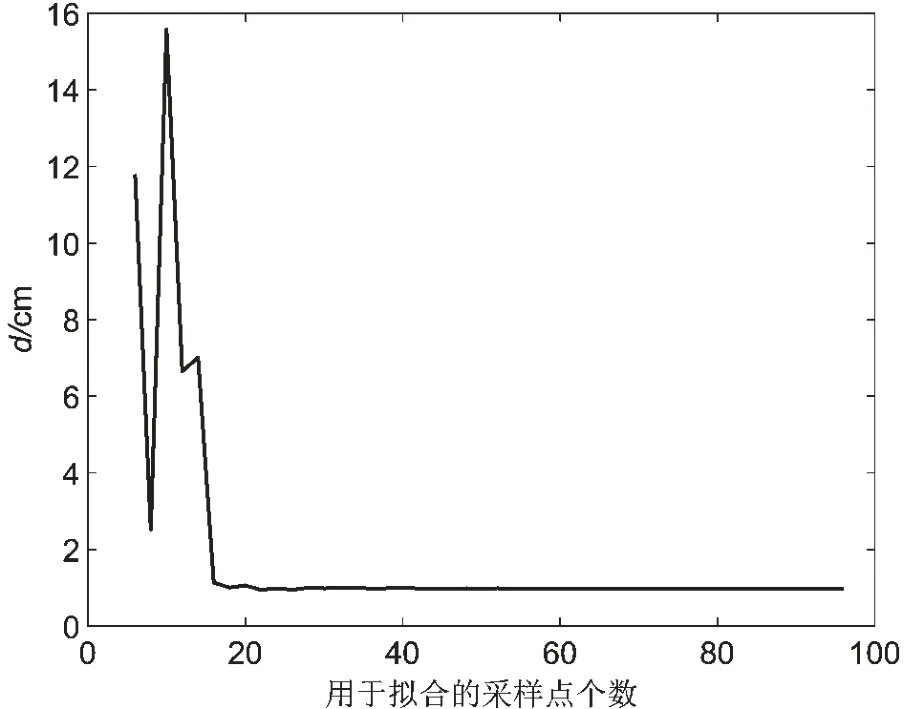
圖9 d 關于采樣點數的折線圖1

改變正方形標定板與坐標系的位置關系后，經實驗證明上述范圍仍然適用。

4.2.2 擬合結果

將m 取為40，擬合結果如表1 所示，顯然無論取標定板的哪組極小值數據去擬合，擬合后的數據均比擬合前的數據更接近設定值，且符合系統精度要求。

4.3 坐標標定結果

直接利用模擬得到的1 600 個測量數據繪制輪廓坐標點如圖11(a)所示。 利用標定過的系統參數對正方形標定板的輪廓坐標進行標定后的結果如圖11(b)所示，顯然標定后的輪廓與真實輪廓接近。

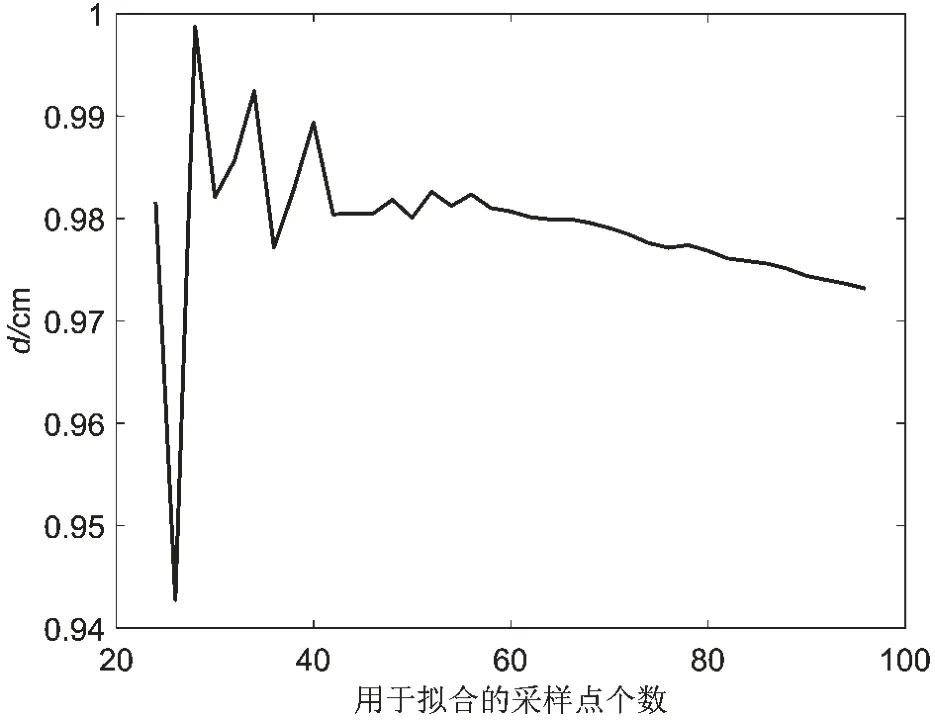
圖10 d 關于采樣點數的折線圖2

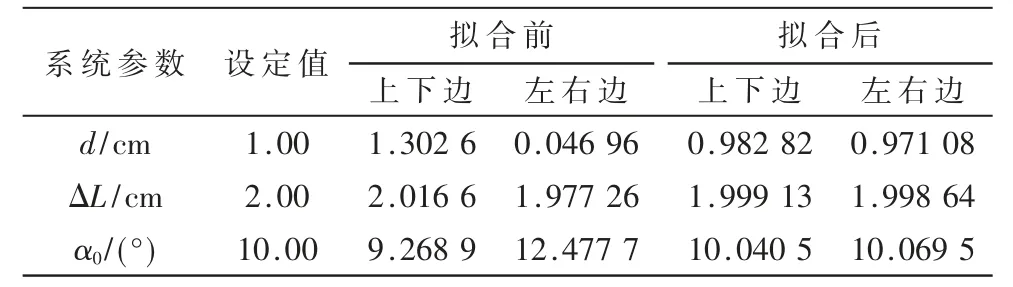
表1 擬合前后系統參數對比

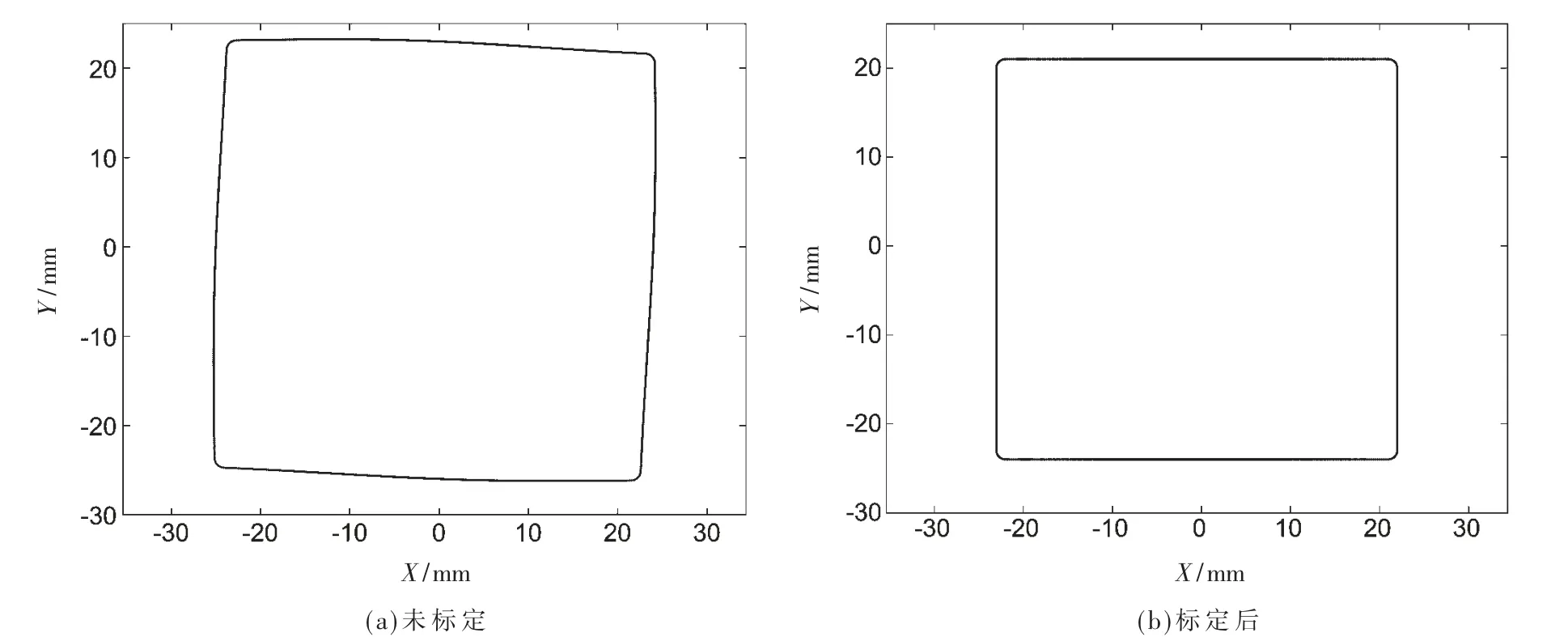
圖11 輪廓坐標圖

5 結論

為解決輪廓掃描儀檢測鉤零點與旋轉平臺的旋轉中心不重合造成的測量長度及角度誤差，本文提出一種利用正方形的特點，通過測量正方形標定板得到的測量數據并經給最小二乘法擬合后計算出輪廓掃描儀的系統參數，進而對測量數據進行處理實現了坐標標定，還原出被測物體的真實輪廓。 并通過Qt Creator 軟件編程模擬仿真了測量過程，用仿真出的數據驗證了算法的可行性。 該方法大大降低了測量儀的制造和安裝要求，通過在線標定即可快速測量被測物體輪廓且滿足系統的精度要求，標定精度高而可靠。