基于工程實例的DFT教學(xué)實踐與探索

王 靜， 楊玲君， 劉開培

(武漢大學(xué) 電氣與自動化工程學(xué)院，湖北 武漢430072)

0 引言

離散傅立葉變換DFT(Discrete Fourier Transform)是“信號與系統(tǒng)”課程的一個教學(xué)重點和難點，其物理意義抽象，公式表達復(fù)雜，學(xué)生掌握和應(yīng)用難度大[3～4]。中國國家標(biāo)準(zhǔn)GB/T17626.7-2008和國際標(biāo)準(zhǔn)IEC61000-4-7: 2002中推薦使用DFT進行諧波檢測[2]。作為電氣與自動化學(xué)院學(xué)生，掌握DFT的基礎(chǔ)基本理論，利用DFT解決實際工程問題，是學(xué)習(xí)信號與系統(tǒng)課程的一項基本要求，也是培養(yǎng)大學(xué)生創(chuàng)新科研能力的需要。

DFT直接在時域離散有限長序列與頻域離散有限長序列之間建立一種變換關(guān)系，可以用計算機進行信號的頻譜分析[1]。為了讓學(xué)生更好理解DFT 的基本概念，本文首先梳理了DFT與離散傅里葉級數(shù)DFS(Discrete Fourier series)、離散時間傅里葉變換DTFT(Discrete Time Fourier Transform)之間的關(guān)系；然后引入電力系統(tǒng)典型的諧波分析案例，設(shè)計實踐教學(xué)環(huán)節(jié)，從而加深對DFT的理解和應(yīng)用。

1 DFT 理論教學(xué)環(huán)節(jié)設(shè)計

在對離散時間信號x(n)進行頻譜分析時，如果x(n)是周期的，周期為N，用DFS計算頻譜，其頻譜是周期為N的離散頻譜，如式(1)所示。

(1)

如果x(n)是非周期的，可以用DTFT計算頻譜，其頻譜是連續(xù)的，如式(2)所示。

(2)

DFT的定義如式(3)所示

(3)

式(3)中，x(n)是時域的離散時間信號，X(k)是x(n)的頻譜，兩者都是長度為N的序列。

比較式(1)和式(3)，可以將DFT看作是將DFS的主值(0～N-1)抽取出來人為定義的一種變換，其目的就是為了能夠?qū)τ邢揲L序列的頻譜進行計算機分析[1]。從物理概念上講，DFS是經(jīng)過嚴(yán)格數(shù)學(xué)推證得到的，符合實際信號特性的，因此它反映了一種客觀的物理現(xiàn)象；而DFT卻不然，因為實際物理信號中不可能存在一個時域有限、頻域也有限的信號。比較式(2)和式(3)，DFT可以看作是將DTFT在一個周期的等間隔取樣，取樣間隔為2π/N。

2 工程案例設(shè)計

隨著智能電網(wǎng)的建設(shè)和大規(guī)模的新能源并網(wǎng)，越來越多的電力電子設(shè)備接入電網(wǎng)，在減少環(huán)境污染和增強電網(wǎng)功能同時也給電網(wǎng)帶來了大量諧波。

2.1 諧波信號數(shù)學(xué)建模

(4)

式中f0=50 Hz，m表示諧波的次數(shù)。

在對諧波進行頻譜分析時，首先要對諧波信號進行采樣，即令t=nTs，Ts為采樣間隔。采樣后的信號表達式如式(5)所示。

(5)

令2πf0Ts=Ω，Ω0為數(shù)字基波頻率，單位為rad。則式(5)可表示為：

(6)

本文為了說明如何用DFT計算諧波信號的頻譜，并便于驗證該算法的正確性，將諧波信號進行簡化，假設(shè)諧波信號如圖1所示，數(shù)學(xué)表達式如式(7)所示。從式(7)中可以看出，該信號包含了基波，3次諧波，5次諧波和7次諧波。

(7)

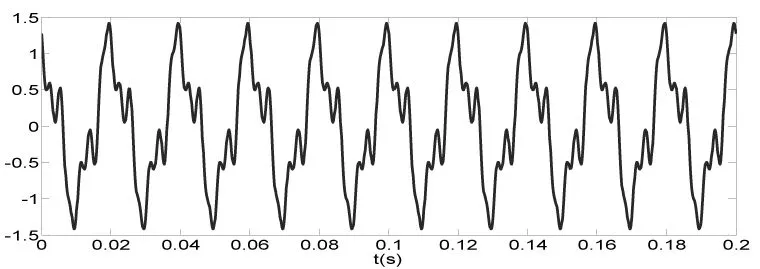
圖1 諧波信號

2.2 諧波信號的離散化處理

利用DFT對諧波信號進行頻譜分析，首先對諧波信號進行采樣，變成離散時間信號。采樣關(guān)鍵參數(shù)是采樣頻率fs和采樣時長T0(采樣點數(shù)N)。根據(jù)采樣定理，對于帶限信號，要求采樣頻率fs大于或等于信號最高頻率的兩倍[1]。在本算例中，要測量的最高次諧波為7次諧波，所以采樣頻率fs至少選取700Hz。如果采樣頻率為700Hz，采樣后的諧波信號如式(8)所示，這里數(shù)字基波頻率Ω0=π/7rad，采樣后得到的離散信號如圖2所示。

(8)

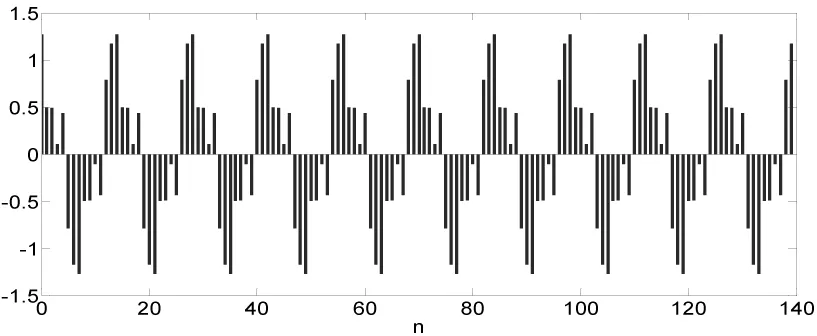
圖2 采樣后的諧波信號

采樣時長T0(采樣點數(shù)N)與離散域頻率分辨率F0有關(guān)。頻率分辨率F0表示應(yīng)用離散傅立葉變換進行頻譜分析時在頻率軸上所能得到的最小頻率間隔。根據(jù)文獻[1]可知，采樣時長T0與頻率分辨率的關(guān)系如式(9)所示：

試劑及耗材：美國MO Bio公司生產(chǎn)的Power-Soil DNA Isolation Kit、百邁克微生物高通量測序建庫試劑盒、美國BioLabs公司Phusion HF MM高保真PCR酶、德國Qiagen公司MinElute?PCR Purification Kit、美國Illumina公司Sample Preparation Kit、全式金Taq DNA Polymerase、北京華大公司的合成引物、西班牙瓊脂糖Agarose、全式金Marker DL5000、Goldview Nucleic Acid Gel Stain等。

(9)

電力系統(tǒng)諧波是工頻(50Hz)的整數(shù)倍，因此要求頻率分辨率為F0≤50Hz，則采樣時長T0≥0.2秒，即至少采樣一個工頻周波，如果采樣頻率為700Hz，則采樣點數(shù)至少為N=T0/Ts=14。

3 基于DFT的工程案例分析

為了治理電網(wǎng)中的諧波污染，確保電網(wǎng)安全運行，快速、準(zhǔn)確的諧波參數(shù)檢測是必不可少的。基于DFT的諧波測量方法是目前最普遍的電力諧波測量方法，也是許多新的諧波測量方法的基礎(chǔ)[5]。

3.1 DFT程序設(shè)計

DFT是為了利用計算機來實現(xiàn)信號的頻譜計算而定義的傅立葉變換，因此程序設(shè)計是實現(xiàn)DFT工程應(yīng)用的前提。本課程建議學(xué)生掌握公式(3)基礎(chǔ)上用Matlab編程實現(xiàn)DFT的計算，程序如下。

function [Xk]=dft(x)

N=length(x);

n=0:N-1;

k=0:N-1;

Xk=0;

for n=0:N-1

Xk=Xk+(1/N)*x(n+1)*exp(-i*2*pi*k*n/N);

end

3.2 采樣頻率的選擇

當(dāng)采樣頻率為700Hz，采樣點數(shù)為14時，計算出的頻譜如圖3所示。

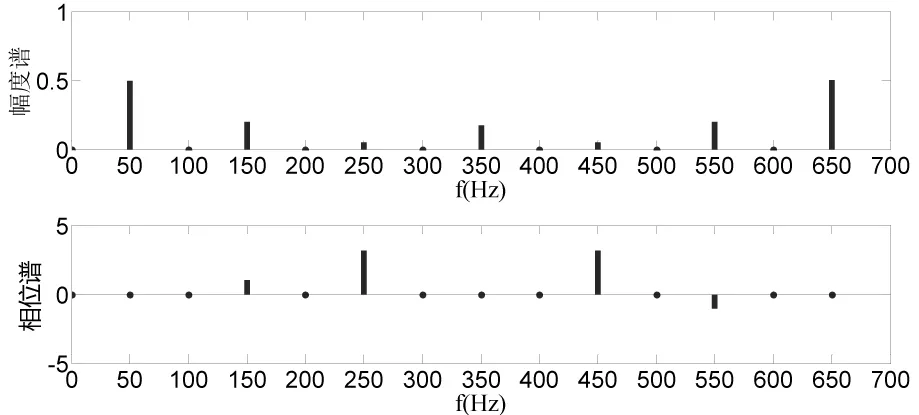
圖3 采樣頻率為700 Hz時信號的頻譜

由DFT的對稱性可知，X(k)的幅值|X(k)|關(guān)于k=N/2偶對稱，幅值為原信號幅值的1/2，相角關(guān)于k=N/2奇對稱的，因此只需考察k=0～2/N，即頻率為0～350Hz范圍內(nèi)的頻譜分布。由圖3可知，基波、3次諧波和5次諧波的計算值與理論值相同，但是7次諧波的幅值和相位有誤差，產(chǎn)生了頻譜混疊。因為諧波信號是正弦信號的疊加，正弦信號的頻譜是沖激函數(shù)，因此不能將諧波信號看作是帶限信號。根據(jù)文獻[6]，對正弦信號采樣時，建議一個周期至少抽樣3個點，即采樣頻率為正弦信號頻率的3倍。因此，對于上述諧波信號，采樣頻率可設(shè)為1200Hz，仍然采樣一個工頻周期，采樣24個點。由于DFT的對稱性，計算所得的頻譜關(guān)于600 Hz對稱，只考察0～600 Hz范圍內(nèi)的頻譜分布，頻譜如圖4所示。

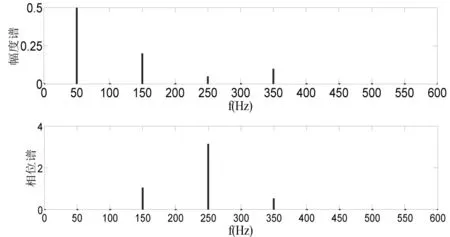
圖4 采樣頻率為1200Hz時信號的頻譜

由圖4可以看出，當(dāng)采樣頻率為1200 Hz時，用DFT計算出的頻譜與理論之完全一致，沒有發(fā)生頻譜混疊。

本案例通過采樣頻率的選擇，讓學(xué)生對正弦信號的頻譜特點、采樣定理的應(yīng)用范圍和頻譜混疊現(xiàn)象有了更加直觀的理解。

3.3 采樣時長的選擇

如果采樣頻率仍取1200，但是采樣點數(shù)取30，即采樣1.25個工頻周期，得到的頻譜如圖5所示。

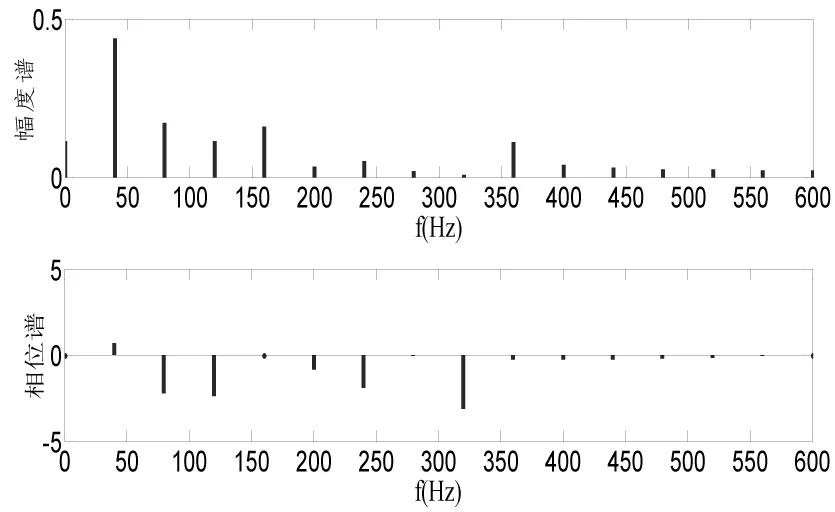
圖5 非整周期采樣時信號的頻譜

從圖5可以看出，由于對諧波信號進行非整周期采樣，發(fā)生了頻譜泄露。在用DFT計算頻譜時，DFT具有隱含周期性[1]，在本例中，采樣30個點，DFT計算時認(rèn)為這30點是一個周期，進行頻譜計算。因此在對正弦信號采樣時，一定要滿足采樣點數(shù)是整個周期[6]。國標(biāo)GB/T17626.7-2008《電磁兼容試驗和測量技術(shù)供電系統(tǒng)及所連設(shè)備諧波、諧間波的測量和測量儀器導(dǎo)則》推薦采樣時長為10個周期，即0.2s，采樣頻率為3200Hz[2]。

本案例通過采樣時長的選擇，讓學(xué)生對DFT隱含周期性、頻譜泄露和周期信號的采樣時長問題有具體的認(rèn)識，起到了開闊思路的良好作用。

4 結(jié)語

本文通過在課堂理論教學(xué)中引入實際工程實例，引導(dǎo)學(xué)生理解和掌握DFT的基本概念，并通過應(yīng)用DFT計算電力系統(tǒng)諧波信號的頻譜，分析DFT計算過程中的參數(shù)選擇問題，使學(xué)生更直觀認(rèn)識頻譜混疊和頻譜泄露現(xiàn)象。教學(xué)實踐表明，將理論知識與工程實例相結(jié)合的授課方式，加深了學(xué)生對理論知識的理解和應(yīng)用，提高了學(xué)生的學(xué)習(xí)興趣和解決實際工程問題的能力，收到了良好的教學(xué)效果。