基于馬爾科夫鏈的電力系統運行可靠性快速評估

毛澍， 張麗*， 談軍， 趙永生， 趙愛華

(1. 國家能源局 電力可靠性管理和工程質量監督中心, 北京 100031；2. 國網電力科學研究院， 江蘇 南京 210000； 3. 國網安徽省電力有限公司， 安徽 合肥 230001)

0 引言

近年來，隨著我國經濟的迅速發展，輸電線路建設變得越來越重要。我國的電力系統增長規模巨大，但越來越復雜的輸電線路和電力系統造成電力系統運行的可靠性降低[1]。同時由于廣泛的地理分布和多變的氣象環境都對電力系統可靠性檢測帶來了很大的困難。因此，通過統計學理論模型，構建一套完整全面的可靠性分析方法對電力企業來說至關重要。我國對此起步較晚，主要開始于上世紀80年代，在1985年成立了電力可靠性管理中心，積極培育輸電系統領域的科研成果[2]。電力系統的可靠性分析重點在于對輸電線路的可靠性，對于電力線路的可靠性分析多采用故障樹分析法、貝葉斯評估法、灰色預測技術和模糊綜合評價等方式[3]。為了高效地處理輸電線路的問題，采用馬爾科夫過程理論，對輸電網拓撲結構的線路故障快速響應，解決輸電線路連鎖故障問題[4]，針對電力系統靈活性差、維護困難的缺點，防御停電的重大事故，保障運行安全。

1 電力系統運行可靠性評估方法

1.1 可靠性概念

可靠性的定義在不同領域有著不同的說法，而對于工業領域來說，通常定義為“設備在規定時間和規定的環境條件下，完成規定功能的概率學意義”。從定義中，可以知道，可靠性是基于時間變量的，可靠性的分布函數設為R(t)，用以表示無故障設備占總體設備的百分率[5]，R的取值范圍是0≤R≤1;不可靠性則設為F(t)，由于兩者是互補的關系，則滿足式(1)。

R(t)+F(t)=1

(1)

假設時間變量T表示從正常工作到設備發生故障的時間，概率密度是f(t)，可靠性的積分函數定義，如式(2)。

(2)

對于設備進行分類，可修復設備與不可修復設備的可靠性估值是不同的[6]。而故障率則表示到某一時刻的失效概率，其利用極限方式進行定義，如式(3)。

(3)

而平均故障率的計算值，如式(4)。

(4)

假設在(t1,t2)的時間段內。

1.2 馬爾科夫隨機過程

馬爾科夫理論的優勢就是無記憶性[7]，尤其在電力系統中，電力系統當前可靠性狀態與歷史狀態無關，而是基于下個未來狀態[8]。同時由于電力系統故障的隨機性，往往使用狀態空間轉移圖來表示輸電線路的全部狀態，通常分為正常運行狀態與故障狀態。馬爾科夫的隨機過程中的參數可以是連續的或者是離散的[9]。對于某一個隨機過程{X(t)，t∈T}，X(t1),X(t2),X(t3),…,X(tn)相應的狀態為a1,a2,a3,…,an∈A。馬爾科夫過程,如式(5)。

P{X(tn)≤an|X(tn-1),…,X(t1)}=P{X(tn)≤an|X(tn-1)}

(5)

而對于馬爾科夫鏈來說，隨機過程{X(t)，t∈T}，n∈T以及狀態為a1,a2,a3,…,an∈A，滿足的條件概率函數,如式(6)。

P{xn=an|x1=a1,x2=a2，…,xn-1=an-1}=P{xn=an|xn-1=an-1}

(6)

式中，{xn,n∈T}就是馬爾科夫鏈。在條件概率P{xn=j,xn-1=i}中，xn=j表示在n時刻系統處在j狀態。因此定義馬爾科夫鏈的轉移概率為P{xn=j,xn-1=i}表示了某個系統在時刻n-1，狀態條件為i時，在n時刻從狀態i轉移到狀態j的概率，記為pij(n)。由轉移概率構成轉移概率矩陣，如式(7)。

(7)

定義設備的故障率和可修復率分別為λ和μ，p(k)表示第k次的轉移概率矩陣，p(k)=pk；p(0)起始向量，n次后的狀態概率向量為p(n)，其關系表達式，如式(8)。

p(n)=p(0)p(n)

(8)

當步數n趨于無窮時，設備平穩狀態下的運行概率為p0，停止運行的概率為p1，如式(9)。

(9)

2 基于馬爾科夫方法的電力系統可靠性模型

2.1 實時運行的可靠性模型分析

輸電線路的電力系統構建可靠性模型會考慮線路自身的老化故障，老化故障的概率涉及輸電線路失效概率密度函數f(t)，與設備使用年齡有關[10]，假設役齡為T年，在后續時間t內產生故障的概率pa，如式(10)。

(10)

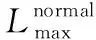
(11)

擬合曲線，如圖1所示。

圖1 基于潮流變化的輸電線路故障概率模型

依據電力系統外界天氣環境的不同，考慮正常天氣狀態與惡劣天氣狀態[11]。假設w=1時，狀態為惡劣天氣；w=0時，狀態為正常天氣。惡劣天氣的持續時間為S，發生故障比例為F，λ為統計平均值。可以得出線路失效的概率，如式(12)。

(12)

由上述結果，電力系統的故障概率，如式(13)。

pc=1-e-λct

(13)

綜合上述的自身故障、線路潮流、外界天氣環境的因素[12]，整體電力系統的可靠性模型綜合故障概率，如式(14)。

p=pb+pc-pbpc

(14)

2.2 基于馬爾科夫的可靠性評估模型

在構建基于馬爾科夫的可靠性評估模型時，首先定義幾個物理量，表示可靠性的指標，分別是可靠度R、可用度A、故障率λ、修復率μ、首次故障前平均時間Tav。在分析基于馬爾科夫鏈模型的電力系統可靠性模型時，將運行狀態劃分為正常狀態、事故狀態和風險狀態[13]。那么電力系統的三狀態模型的狀態轉移概率矩陣，如式(15)。

(15)

Пi是ti時刻的電力系統狀態分布，如式(16)。

(16)

假設電力系統的初始狀態為П(0)，經過m個Δt之后的電力系統轉移，如式(17)。

C(m)=C(m-1)P=C(0)Pm

(17)

電力系統的長期穩定運行狀態概率，如式(18)、式(19)。

(18)

(19)

將式(14)寫成分塊矩陣形式，如式(20)。

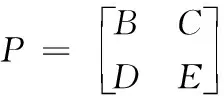
(20)

式中，B表示電力系統的接受狀態轉移的概率；C表示從非接受狀態到接受狀態轉移的概率；D表示電力系統從不可接受狀態向可接受狀態轉移的概率；E為電力系統在不可接受狀態間轉移的概率。當分塊矩陣D=0，E=I時，此時的馬爾科夫模型，計算電力系統的首次故障前平均時間，如式(21)。

(21)

3 基于馬爾科夫方法的可靠性仿真分析

從上述的分析中系統采用IEEE RBTS BUS6配電系統作為算例應用系統。其等值電網接線圖，如圖2所示。

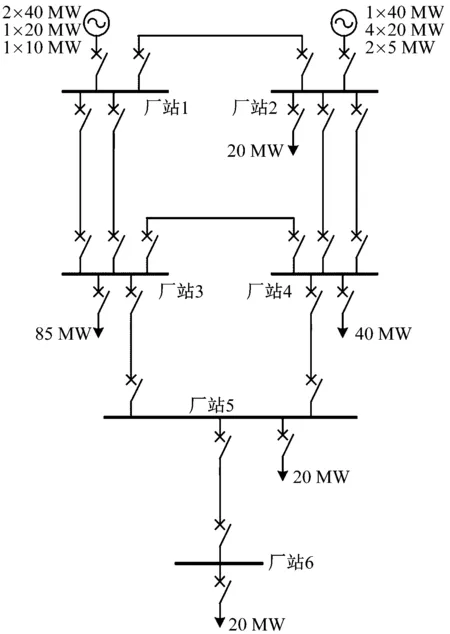
圖2 IEEE RBTS BUS6等值電網接線圖

包含負荷基本數據、網絡拓撲結構等等數據。首先假設Δt時間的時間間隔內的電力系統的故障率為0.000 5，修復率為0.014。為了驗證馬爾科夫鏈模型，保持其他電力元件的故障率為0。通過常用的蒙特卡洛方法對RBTS BUS6配電系統進行數據模擬，統計經過8 000次模擬后的系統狀態變化情況，如表1所示。

通過狀態轉移數據的分析，獲得電力系統的狀態轉移概率矩陣，如式(22)。

(22)

每次模擬的開始都是從狀態1起，t=0時作為電力系統無故障狀態，如式(23)。

П (0)=[1 0 0]

(23)

將式(22)、式(23)代入到式(16)，經過300次矩陣乘法，可以得到П (1)- П (300)的值，通過模擬，可以得到模擬值П′ (1)- П′(300)。其對比圖，如圖3—圖5所示。

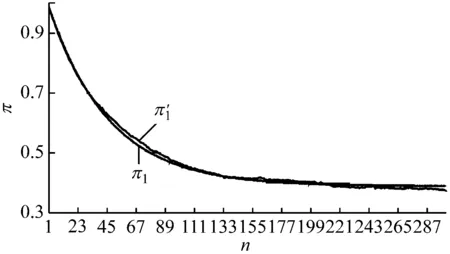
圖3 300個時間間隔內電力系統的解析值與統計值處于狀態1的概率對比圖

圖4 300個時間間隔內電力系統解析值與統計值處于狀態2的概率對比圖

圖5 300個時間間隔內電力系統解析值與統計值處于狀態3的概率對比圖

圖3—圖5分別顯示處于狀態1、狀態2、狀態3的概率。對于解析值與統計值的誤差可以通過式(24)得到。

(24)

本電力系統中，各個電力元件的故障概率值較小，8 000次模擬結果中，有3 030次電力系統處于狀態2的條件。為了精確得出故障前平均時間，將時間間隔內的故障概率和修復概率修改成0.113 1、0.285 4，重新代入到馬爾科夫模型進行模擬，統計得到狀態轉移概率矩陣，如式(25)。

(25)

則可以由式(20)得到故障前平均時間為6.994 1s，而由統計結果計算出的故障前平均時間為7.614s。上述結果說明由基于馬爾科夫模型的狀態轉移概率矩陣得出的解析值，與進行電力系統的統計值相一致。電力系統的可靠性通過馬爾科夫鏈模型可以進行快速的評估，更為簡單和實用。

4 總結

電力系統的可靠性評估問題已經成為電力領域中長期困擾企業的問題。是電力企業發展的重要系統工程。首先總結了電力系統的當前研究現狀以及輸電線路的發展趨勢。在總結了3種可靠性分析方法后，采用馬爾科夫理論模型。為了提高電力系統的可靠性，本文充分論證了狀態空間轉移的性質。由電力系統的狀態轉移概率矩陣P解析系統狀態的轉移變化。依據首次故障前平均時間的可靠性指標，用于檢修、規劃電力系統的實際運行狀態。從而使得電力企業的維護設計更加靈活，也為智能電網的發展帶來極大的參考意義。在后續的研究中，還會考慮電力變壓器、開關設備的影響，同時增加對可靠性參數及電力負荷不確定性的影響。