高空帶電機器人軌跡跟蹤與控制研究

胡仕成，陳志高，黎新齊

(中南大學 機電工程學院，湖南 長沙 410083)

由于高壓電網絡線路長、分布廣、線路環境復雜、作業空間狹小等特點，給人工帶電作業開展帶來巨大困難，高空帶電機器人的出現可以有效地解決上述困難。通過自主和遙控操作靈活切換能替代人完成復雜環境下的支線線路引線搭接等高危工作。

由于工作環境的復雜性和控制系統存在的滯后性，導致了高空帶電機器人工作效率和工作精度的低下，要實現機器人的自動化和智能化，需要一種高空帶電機器人軌跡跟蹤控制方法，提高控制系統的響應速度、控制精度。

相關專業人士提出了一種作業平臺的軌跡跟蹤控制方法，通過對液壓閥控系統特性研究，設計了相應的PID控制器優化其系統，使得工作斗位置跟蹤波動范圍小于±200mm，采用PID 控制、負反饋以及前饋的復合控制來實現臂架直線軌跡控制。

針對高空帶電機器人臂架控制問題，本文通過建立高空帶電機器人臂架三維模型和臂架系統簡圖，對臂架進行運動學分析，推導出抓手相應軌跡下兩個變幅液壓缸的運行軌跡，并提出了一種PID 優化控制方法來提高控制系統的響應速度、控制精度。并在MATLAB/Simulink 環境下進行仿真，比較優化前后系統的響應速度和控制精度。

1 高空帶電機器人的臂架控制系統總體設計

1.1 臂架三維模型

高空帶電機器人主要包括臂架系統和液壓控制系統，臂架系統包括底座1、豎直臂2、水平桿3、伸縮桿4、擺動桿5、抓手6 組成。臂架系統如圖1 所示。

1.2 臂架運動學建模及軌跡跟蹤

根據臂架系統原理，建立臂架結構簡圖，如圖2 所示：將高空帶電機器人工作臂簡化為四關節的機器人手臂，采用D-H 坐標法對臂架四個桿件建立相對坐標系，并引入連桿扭角α，連桿長度a，關節轉角θ，關節距離d 四個參數來描述每個桿件的相對位置，建立其臂架的運動學數學模型。

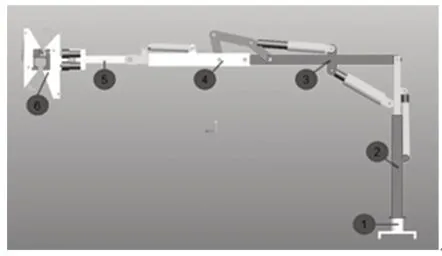
圖1 高空帶電機器人三維模型

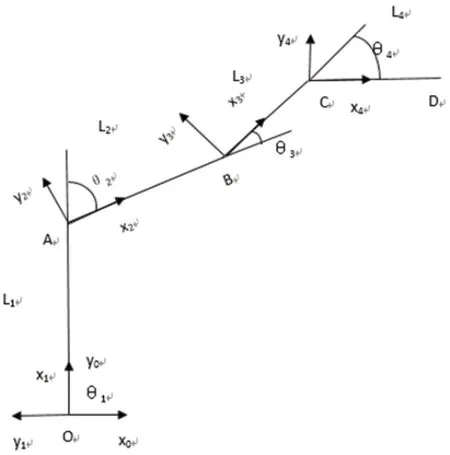
圖2 D-H 坐標系

如圖2 所示，以O 點作為作為整體參考坐標原點，四個桿件從原點開始編號，分別依次為1、2、3、4 號桿件，桿件長度分別對應記為L1、L2、L3、L4，以各桿件首端位置作為局部坐標系的原點，即圖2 中的O 點、A 點、B 點、C 點，桿件與其局部坐標系x 軸之間的夾角為關節轉角θi，i=1，2，3，4；di為接續公垂線的偏距，即相鄰桿件的軸向的距離。運用機器人學，根據Craig D-H 坐標系，得到桿件坐標系下相鄰桿件之間的位姿矩陣：其分別表示桿件首端相應于局部坐標系的轉換矩陣。

根據各個相鄰關節的坐標變換矩陣，可以得到第四關節相對于整體坐標原點變換矩陣。

由于建立的D-H 坐標系是Craig D-H 坐標系，所以還需要建立第四關節末端D（即高空帶電機器人抓手位置）相對于整體坐標原點的變換矩陣，首先，D 點相對于局部坐標系4 的位置變換矩陣為：

由此坐標系可以得出D 點相對于整體坐標系原點的變換矩陣為：

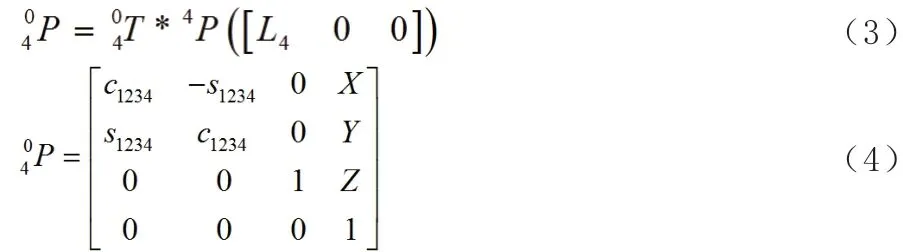
由式（8）可以得出臂架關節轉角θ 與抓手在基坐標系間的幾何關系：

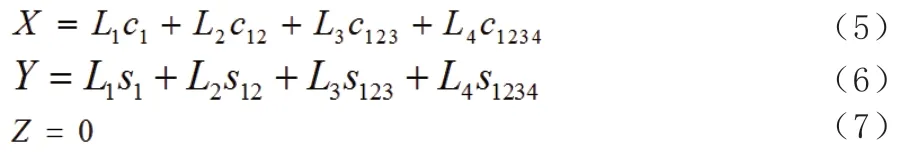
故高空帶電機器人臂架末端抓手坐標為：

為方便輸出圖形，只關注遍歷算法，不用思考計算輸出圖形的坐標位置，因此不考慮在命令行中打印二叉樹，而是采用DOT圖形描述語言。DOT是純文本圖像描述語言，文件擴展名通常是.dot，需要有專門的程序處理這些文件并將其渲染成為圖片。Graphviz是貝爾實驗室開發的一個開源的圖像可視化的軟件，它使用dot作為腳本語言，然后使用布局引擎來解析此腳本，并完成自動布局。

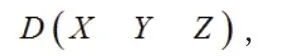
高空帶電機器人的最大作業高度為：

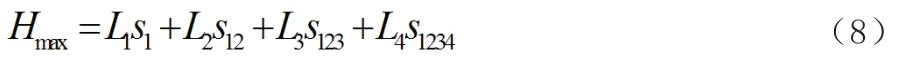
最遠工作長度為：

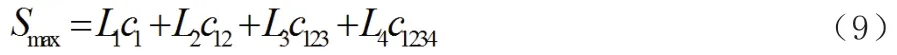
機器人工作臂的 D-H 參數表，如表1 所示。

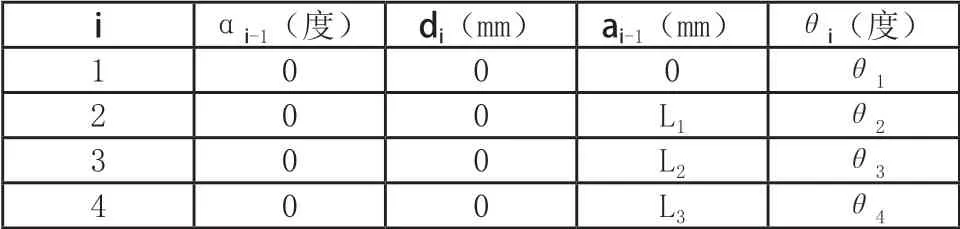
表1 臂架Craig D-H 參數表

2 臂架液壓數學模型的建立

高空帶電機器人臂架液壓控制系統采用的閉環控制，由高空帶電機器人臂架采用的是變幅液壓控制系統，該系統是通過對電液比例換向閥的控制進而實現液壓缸的工進和返回的。接下來，將根據電液比例系統原理進行數學模型的建立，推導出該系統的傳遞函數。

電液比例閥的數學模型為：

參考文獻得閥控液壓缸的傳遞函數可以近似為：

位移傳感器的數學模型視為比例環節：

綜上所述，電液比例系統的傳遞函數為：

臂架變幅液壓系統數學模型的相關參數數值如表2 所示：

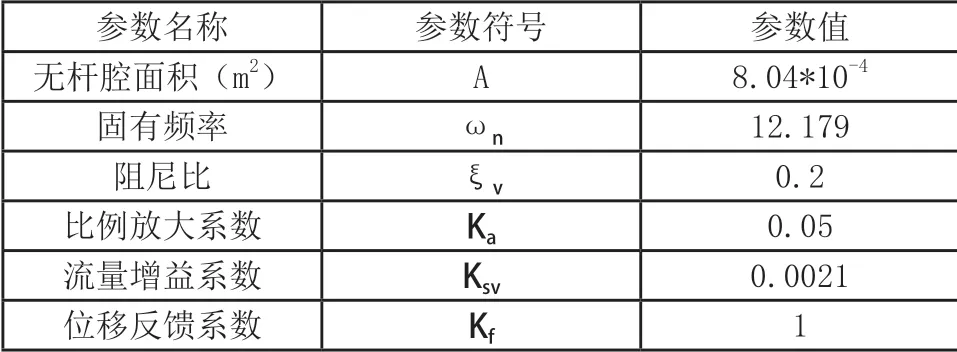
表2 數學模型相關參數

3 MATLAB/Simulink 建模及仿真分析

為了驗證PID 的控制效果，建立PID 優化控制系統仿真模型，仿真模型如圖3 所示，模型包括目標響應環節、實際響應環節和PID 響應環節三個部分組成，主要對其三種環節的仿真結果進行分析，其中目標響應環節和實際響應環節的參數設置與上文相同，PID 響應環節首先要對PID 控制器的三個參數進行設置，PID 參數設置方法包括試湊法、Ziegler—Nichols 整定法、臨界比例度法、衰減曲線法等方法。該仿真通過試湊法對PID 控制器的比例系數、積分系數和微分系數不斷進行調節，觀察系統響應曲線，獲得系統最優響應。

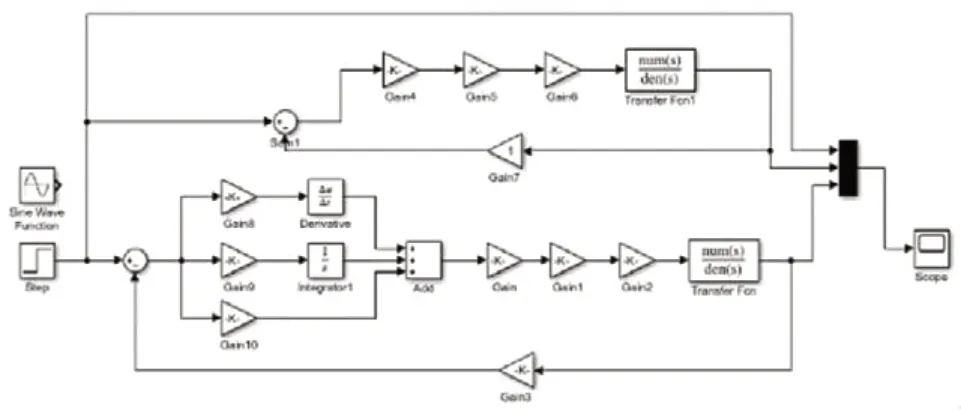
圖3 變幅液壓系統PID 優化仿真模型

經過多次對PID 控制器三個系數的調節和響應數據曲線的比較，發現在比例系數取值為15、積分系數取值為0.1、微分系數取值為0.001 的情況下，系統響應最優，系統調節時間較短，滯后程度較低，PID 優化后的控制系統在給定階躍控制信號后，1 秒達到期望值，相對優化前的響應滯后7 秒，系統響應速度提高了85.7%，但只是在響應期間，有輕微的波動，由于對系統不會產生較大影響，可以忽略。

PID 優化后的控制系統在給定正弦信號后，系統響應曲線與目標曲線非常接近，只是有0.2 秒的滯后，其響應的峰值也完全相同，相對于優化前的系統響應，在響應時間上和控制信號的期望響應上面都有較大的改善，綜合性能有了很大提高。

4 結語

根據高空帶電機器人臂架運動特點，首先，簡化臂架結構，應用D-H 坐標法建立臂架運動學模型，得到機器人抓手的運動數學模型。其次，臂架液壓控制系統與PID 控制相結合，可以有效解決系統響應滯后的問題，階躍控制信號在PID 優化控制后，系統響應時間縮短85.7%，正弦控制信號較優化前系統響應縮短至0.2 秒，響應峰值也與目標值完全相同。

圖4 PID 優化前后的系統響應對比圖