基于CAID的工業設計透視草圖三維模型重建方法*

徐明亮， 段景輝

(三亞學院 a. 藝術學院， b. 信息與智能工程學院， 海南 三亞 572000)

在進行工業設計時，設計師往往都會將其自身的創意與設計理念通過繪制產品草圖與效果圖來實現[1].CAD技術出現后，工業設計可直接通過三維造型實現.然而大部分優秀的設計師更加喜歡通過手繪的方式畫出產品效果圖[2].傳統CAD系統僅可完成建模，無法將創意可視化，導致繪制產品效果圖與自身創意不符.計算機圖像技術的發展，令計算機識別草圖構建三維模型成為可能.

目前，常用的三維模型重建方法主要有基于RHINO的模型重建方法[3]、基于非量測相機圖像的設計圖模型三維重建方法[4]和自由形態建模方法[5]等，然而上述方法均需對深度坐標進行計算，建模周期長、成本高，實現過程復雜.本文在計算機輔助工業設計(CAID)軟件設計的基礎上，提出一種工業設計透視草圖三維模型重建方法.

1 材料與方法

計算機輔助工業設計技術為工業設計理論和CAD技術的結合，能夠和工業設計特點與工業設計師設計思維相適應.CAID系統將工業設計知識當成主體，將計算機當成輔助設計工具[6]，充分展現了工業設計理念，完成對設計的定量化描述，借助計算機快速高效的特點，令工業設計效果更加合理化.

基于CAID的工業設計透視草圖三維模型重建方法主要包括兩個重要階段，首先需對透視草圖進行識別，然后對其進行三維模型重建.

1.1 透視草圖識別

通過分步處理的方式對透視草圖進行識別，先依據草繪筆劃特征對筆劃進行分段，然后對其進行識別.

1.1.1 草圖筆劃分段

筆劃分段又被稱作關鍵點檢測，關鍵點就是筆劃的分段點，通常是拐點或角點[7-8].關鍵點檢測主要是按照筆劃特征，對用戶設計意圖進行捕捉，把某個筆劃分割成若干子段[9].因為只通過某類信息對筆劃進行分段會造成分段點數量太多，按照用戶草繪習慣，通過草繪過程中筆劃的特征對筆劃進行分段處理，詳細過程如下：

1) 對輸入點集合Pj中不同點的坐標進行采集，對角度范圍閾值A、速度范圍閾值V以及曲率范圍C進行初始化處理.

2) 通過下述公式求出與兩向量相連的角度值aj，其表達式為

dj=|Pj+1-Pj|

(1)

d′j=|Pj+2-Pj|

(2)

(3)

式中：dj為相連兩點間的間隔；d′j為每間隔一點后兩點間的間隔.

3) 第j點的速度值vj的計算公式為

(4)

式中：Δdj為兩個向量的長度偏差；t為采樣所需的平均時間.

4) 相連兩個點的近似曲率改變值Δej的計算公式為

(5)

(6)

Δej=ej+1-ej

(7)

式中：ej為第j點的近似曲率值；δj為向量PjPj+1和x軸間的夾角.

5) 如果δj小于A，則認為Pj+1為分段點，將其添加至集合Pout中.如果δj角度在[170°，180°]范圍內，且vj低于V，|Δej|≤C，那么Pj為分段點，將其添加至點集中.

6) 把透視草圖筆劃的第一個點和最后一個點當成分段點添加至點集Pout中.

7) 輸出點集Pout.

1.1.2 圖形擬合與識別

圖形擬合即找到和輸入筆跡相近程度最高的圖形，筆跡分段則把所有筆跡都分成準直線，所以僅需通過最小二乘法進行直線擬合即可[10-11].

針對透視草圖每條筆跡，通過鏈表形式對其進行保存.可將筆跡R當成是m個像素P(i)的集合，即

R={P(i)=(x(i)，y(i))}

(8)

式中，x(i)與y(i)為像素點的坐標.針對各草圖筆跡，通過下述過程進行分析：

1) 對筆跡是否是折線進行判斷，獲取筆跡首尾點P(0)與第m-1個P(i)，計算由P(0)與第m-1個P(i)相連的直線方程L.

2) 獲取筆跡的長度與寬度，對閾值τ進行計算.

3) 把R中不同點P(i)與直線L間的間隔d(i)和閾值τ相比，如果d(i)<τ，則認為筆跡是直線，通過直線擬合獲取端點值.如果d(i)≥τ，則認為筆跡是折線，需對其進行處理.

4) 求出R中不同點P(i)和L間的間隔，獲取間隔值最大的點，將其當成角點，把角點保存至角點序列Sii中，從該角點處對筆跡進行分段處理.

5) 對新分段的筆跡繼續進行折線判斷，直至獲取全部角點.

按照順序對手繪草稿過程中角點序列進行排序，獲取新的角點序列Sii，對角點序列中Sii-1、Sii、Sii+1進行處理分析，獲取Sii-1與Sii+1連成的直線段L1L2，計算Sii到線段L1L2的垂足O，如果O在線段L1L2中，則繼續對其進行處理；反之對下一個角點組進行同樣分析.求出Sii與線段L1L2間的間隔d，如果d低于閾值τ，那么Sii為偽角點，將其從角點序列中刪除，對下一角點組進行處理[12].

依據新角點序列對保存的草圖筆跡數據鏈表進行分段處理，獲取分段后各條直線的鏈表，完成對其的直線擬合，獲取不同端點值，實現對草圖的識別.

1.1.3 草圖規整

草圖規整即把初步識別獲取的線元集轉變成規則的幾何圖形，是透視草圖三維模型重建的基礎與關鍵[13-14].因為初步識別獲取的為零散的線元，未得到最終的空間關系.透視草圖規整即判斷零散線元可能存在的幾何關系，同時引入約束，形成規則的幾何圖像.

透視草圖中含有設計者的設計意圖，按照所處環境找到線元可能的空間關系是規整的重要階段[15].采用依據規則與透視草圖上下文的方式完成規整，保證了多圖元的規整.依據規則對圖元和坐標軸的位置關系進行判斷，確定圖元間的連接關系.具體方法如下：

1) 依據規則完成判斷.如果圖元和坐標軸夾角在既定閾值范圍內，即可確定位置關系是垂直、平行或特殊角度.

2) 依據草圖上下文完成判斷.如果兩個圖元端點間間隔在既定閾值范圍內，那么將后一圖元端點位置進行改變，實現端點融合.如果橢圓中心和直線間最近間隔與周長之比在既定閾值范圍內，表明是相切.如果橢圓中心點間隔在既定閾值范圍內，則表明是通信.如果線元間長度之比在既定閾值范圍內，則表明是等長.

1.2 透視草圖三維模型重建方法

在進行工業產品設計的過程中，特別是對構形進行設計時，一般通過趨近正等軸側投影圖的透視草圖形式進行描述.在構形時繪制的線條大部分是消隱的軸測圖，如圖1a所示，其和通常所見的圖形中最接近的可行解用圖1b進行描述.所以將封閉的各面片當成三維模型重建的關鍵，在CAID軟件下逐步完成透視草圖相應形體的三維重建.

通過圖1b所在的坐標系，結合投影的相關知識可知，軸測圖可利用異中求同法獲取.首先以y軸為核心順時針旋轉θ1角度，然后以x軸為核心逆時針旋轉θ2角度，再向xoy平面進行正投影轉換處理.獲取的軸測映射轉換矩陣為

圖1 透視草圖和可行解

(9)

利用G=[X，Y，Z，1]代表圖中各頂點的齊次坐標，在進行軸測轉換之后可得到相應頂點的齊次坐標，即g=[x，y，0，1]，符合g=GT的映射關系，其中，T為描述轉換矩陣.

若軸測圖中不同定點映射的二維坐標是確定的，在理論上可利用軸測映射轉換的逆轉換，即G=gT′，其中，T′為逆轉換矩陣，計算頂點三維信息，完成圖形的三維重建.然而在實際應用中，分析軸測映射轉換矩陣T可知，其沒有逆矩陣，無法完成逆轉換.

經識別與規整處理后的透視草圖空間圖形由多個表面構成，將不同面片當成三維重建對象進行分析.利用n=(a1，b1，c1)描述面片的單位法向矢量，則面片上不同頂點的三維坐標平面方程為

a1X+b1Y+c1Z+d1=0

(10)

為了解決軸測映射轉換矩陣無法變成逆矩陣的問題，對轉換矩陣T進行調整，獲取的矩陣為

(11)

經調整后，符合g=GR的映射關系，然而當前矩陣R可逆，則有G=gR′，也就是只要獲取面片的法向矢量，以及面片中不同頂點映射的二維坐標值，即可獲取相應頂點的三維信息.

在進行透視草圖三維模型重建時，可隨機針對某面片進行重構，按照該面片和其他面片間的連接關系，對全部面片進行分層分布求解，實現整個透視草圖的三維模型重建.

1.3 三維模型重建時面片擴展

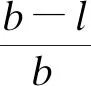
(12)

如果q與q″間的間隔過大，或可能出現斷層的情況下，僅通過n(q)對n(q′)進行初始化處理，假設γ=α，則有

(13)

利用Δ(a，b)表示q與q″間的關系.首先令a、b低于閾值，提高q與q″的相關性.擴展面片的可見圖片集合V(q′)主要包含兩部分：1)當前面片的所有可見圖片集合V(q)；2)最近面片可見圖片集合V(q″)，把滿足角度約束的圖片添加至擴展面片的可見圖片集合中，則有

V(q′)=V(q)+{n(q′)J(q′)}

(14)

在判斷擴展面片中心J(q′)的情況下，通過J(q′)和q所處平面垂直距離獲取，J(q′)和面片q所處平面垂直距離計算公式為

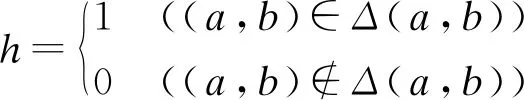
(15)

完成對n(q′)、J(q′)和V(q′)的初始化處理后，通過共軛梯度法對擴展面片q′的位置與方向進行調整，收斂后獲取面片q′，也就是擴展的新面片，對其進行三維重構，直至擴展至整個圖形.面片擴展過程示意圖如圖2所示.

2 結果與分析

實驗在CAID軟件下進行，對本文方法進行實驗驗證.圖3為椅子的建模實例.圖3a為設計師手繪的透視草圖，圖3b為經識別處理及規整后圖形，圖3c為經本文方法得到的三維模型重建結果.透視草圖中各特征點的坐標如表1所示.

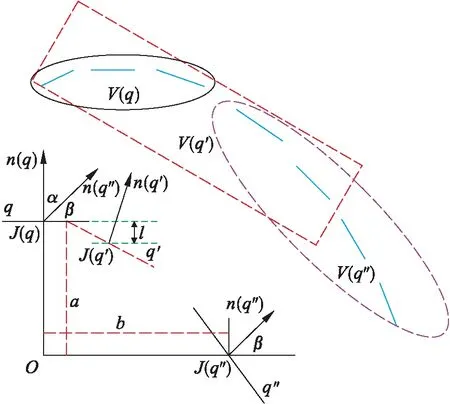
圖2 面片擴展過程示意圖

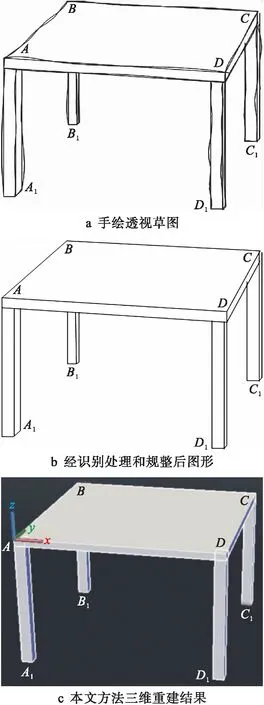
圖3 對草圖的三維重建實例

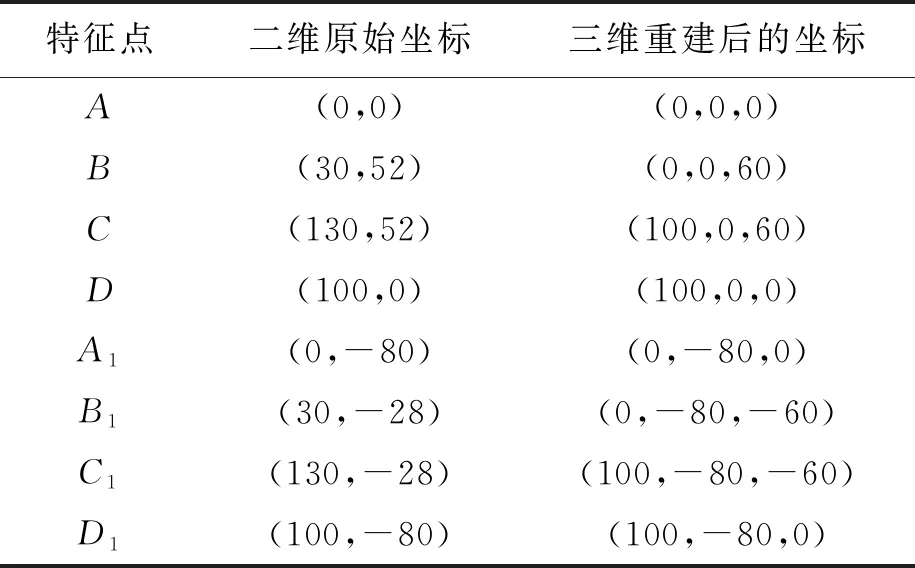
表1 透視草圖中各特征點坐標統計

分析圖3可以看出，采用本文方法對椅子透視草圖進行三維模型重建，得到的重建結果可滿足要求，生成了用戶所需的模型，是一種有效的三維模型重建方法，可應用于實際的工業設計中.

為了驗證本文方法的可行性與精度，設計實驗測試模型.在空間直角坐標系中，把研究幾何體以y軸為軸心順時針轉角45°，繞x軸逆時針轉角40°，在二維面中進行正映射轉換，由此得到物體不同頂點的二維坐標值.

根據所提的三維模型重建方法，結合標準差計算法準確獲取重建圖形不同頂點坐標.對重建結果與原始坐標進行比較，不同坐標間的差異就是計算誤差.因為重建過程是通過擴展實現的，所以將頂面作為基礎面，將頂面和側面之間的夾角當作夾角.理論情況下，當前地面和頂面大小相同時，模型變形系數為1，夾角為90°.

為了進一步研究本文方法的重構精度，設計了一組相似性測試算例.將A、B、C、D四個特征點在重建后與平面豎直方向的夾角與理論夾角相對比，以此驗證重建精度.在進行測試時，將本文方法作為實驗組，將文獻[3]中的基于RHINO的重建方法和文獻[4]中的基于非量測相機圖像的重建方法作為對比組，針對相似算例進行重建，結果如表2所示.

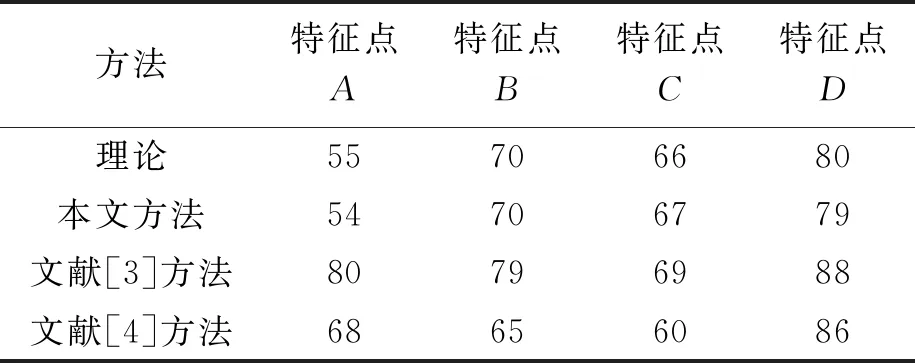
表2 三種方法三維模型重建精度比較

分析表2可知，采用本文方法對透視草圖進行三維模型重建，得到的特征點夾角和理論夾角基本一致，說明本文方法重建坐標和理論值最為接近，偏差明顯低于文獻[3]中的基于RHINO的重建方法和文獻[4]中的基于非量測相機圖像的重建方法，證明本文三維模型重建方法重構結果和理論值基本吻合，重建精度高，可行性強.

3 結 論

通過分析基于CAID的工業設計透視草圖三維模型重建方法，得出如下結論：

1) 按照用戶草繪習慣，根據草繪過程中筆劃的特征對筆劃進行分段處理，找到和輸入筆跡相近程度最高的圖形，筆跡分段把所有筆跡都分成準直線，采用最小二乘法進行直線擬合，實現圖像擬合.把初步識別獲取的線元集轉變成規則的幾何圖形，實現草圖規整，為透視草圖三維模型重建提供依據.

2) 經識別與規整處理后的透視草圖空間圖形看作由多個表面構成，將不同面當成三維重建的對象進行分析，根據面的法向量以及各個面中不同頂點的坐標值，獲得各頂點的三維坐標.在面的擴展過程中，只按照當前面信息對面進行擴展，未綜合利用其余面信息，擴展結果連接性較差，同時考慮左右相鄰面對擴展面產生的影響，可令三維重建結果更加光滑.

3) 實驗結果表明，采用本文方法對椅子透視草圖進行三維模型重建，得到的重建結果可滿足要求，得到的夾角和理論夾角基本一致，偏差最小，說明所提三維模型重建方法重構結果和理論值基本吻合，重建精度高，可行性強.