基于T-S模糊神經網絡的三葉回轉石灰窯智能控制

陳作炳，劉 盼，劉 陽,陳 響

(武漢理工大學 機電工程學院，湖北 武漢 430070)

煅燒石灰的回轉窯是一個多輸入多輸出、非線性、多耦合的復雜系統，具有大慣性、純滯后、時變性等不穩定因素，因此石灰窯數學模型的建立非常困難。要做到穩定生產、高質量、低消耗和低污染，對煅燒溫度的控制十分重要，傳統控制方案難以滿足控制要求[1]。新型三葉回轉石灰窯以天然氣作為燃料生產生石灰，相比傳統回轉窯可大大提高熱利用效率，節能環保。將模糊神經網絡控制應用于新型三葉回轉石灰窯控制系統中能夠準確控制石灰窯的煅燒溫度[2-3]，提高活性石灰質量，降低能源消耗。

1 三葉回轉石灰窯工藝與特點

三葉回轉石灰窯屬于臥式窯，與傳統回轉石灰窯工藝過程相似，其工藝流程如圖1所示。石灰石從立式預熱器預熱室內緩慢下移，窯尾高溫空氣通入預熱室，石灰石在預熱器內發生部分分解后經石灰窯溜槽進入石灰窯，在石灰窯內與逆向流動的高溫氣體接觸進行煅燒[4]。石灰窯安裝熱電偶測量窯內不同位置的溫度，窯內的三葉結構使物料在窯內不斷回轉，充分進行熱交換。煅燒后的石灰經過窯尾立式冷卻器冷卻。窯頭的燃燒器采用天然氣作為燃料，減少對環境的污染，助燃風采用通過立式冷卻器的熱風，提高熱利用效率。

圖1 三葉回轉石灰窯工藝流程

三葉回轉石灰窯的獨特結構使其熱利用效率比傳統石灰窯高，實現節能降耗的目的。其剖面結構如圖2所示，窯尾為三葉弧形葉片部分，窯頭為耐火磚部分。物料自窯尾向窯頭流動過程中發生分解反應，生石灰從窯頭出料。三葉回轉石灰窯的弧葉部分截面結構如圖3所示，從外至內依次為外筒體、絕熱涂層、澆筑層、弧形葉片。三葉弧形葉片使用310S不銹鋼作為耐高溫材料，內部圓弧形鋼板分段相互焊接，使得物料隨著回轉窯旋轉而得到充分的翻轉，改善了傳熱過程，能夠保證物料在回轉窯內部均勻煅燒，大大提高分解效率和窯的熱使用效率[5]。

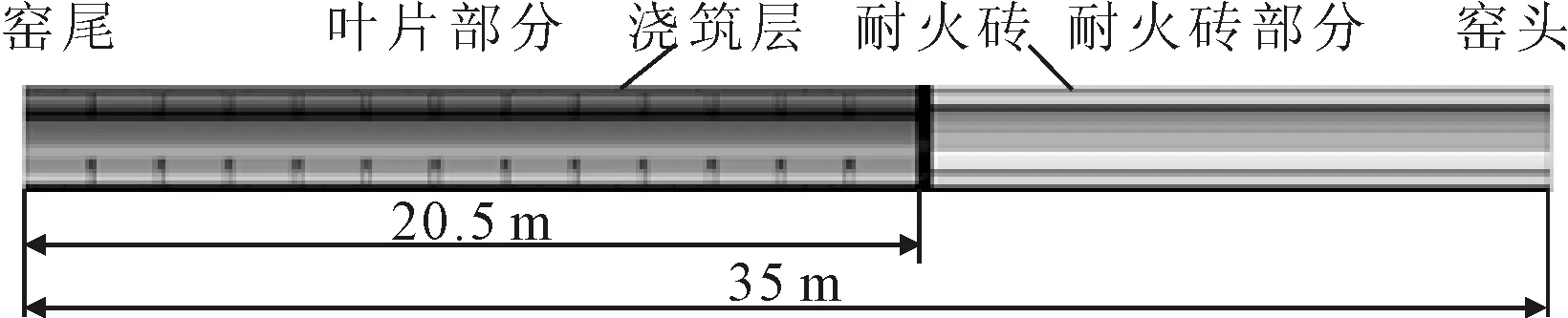
圖2 三葉回轉石灰窯剖面結構圖

圖3 三葉回轉窯截面結構圖

2 T-S型模糊神經網絡算法

2.1 T-S模糊神經網絡

T-S(takagi-sugeno)模糊神經網絡是一種非線性模糊推理模型[6-7]，具有表達模糊推理規則、計算簡單、利于數學分析的優點，其網絡結構如圖4所示，第一層為輸入層，各個節點直接與輸入相連接，該層的節點數為系統輸入的個數n。

圖4 T-S模糊神經網絡結構

(1)

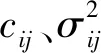
第三層的每個節點代表一條模糊規則的匹配，計算每條規則的適用度，即

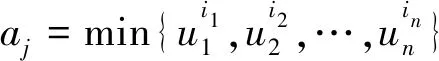
(2)

第四層的節點數和第三層相同，第四層的作用是實現歸一化處理，即

(3)

第五層是輸出層，它實現的是清晰化計算，即

(4)

式中，wij相當于yi的第i個語言值隸屬度的中心值。

2.2 T-S模糊神經網絡算法

T-S模糊神經網絡在結構上與前饋神經網絡相同，可采取前饋神經網絡的學習算法，即BP網絡的誤差反向傳播算法來調整參數。誤差傳播算法是利用樣本數據和網絡輸出的差值作為系統誤差，通過不斷向前層求誤差變化率來調整網絡權值[3]。

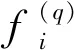
(5)

式中：ydi和yi分別為期望輸出和實際輸出。

(6)

(7)

(8)

(9)

(10)

(11)

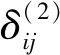
3 石灰窯模糊神經網絡建模與訓練

3.1 石灰窯模糊神經網絡設計

在石灰窯煅燒石灰石控制過程中，煅燒帶溫度受窯頭燃料量的影響最大。 同時，助燃空氣風機的風量和窯轉速也會對燃料的燃燒和煅燒帶溫度有所影響，選擇煅燒帶溫度和溫度變化率作為網絡輸入，燃料量、助燃空氣量作為控制參量[8-9]。

該模糊神經網絡模型設計為兩輸入、兩輸出，模型網絡共有5層：第一層為輸入層、第二層為輸入隸屬度、第三層為規則層、第四層為歸一層、第五層為輸出層，其模糊神經網絡結構模型如圖5所示。x1,x2分別為煅燒溫度和和煅燒溫度變化率，y1,y2分別為天然氣流量和助燃空氣流量。

圖5 石灰窯模糊神經網絡模型

由于模糊神經網絡中輸入節點的物理量不同，同時同節點的物理量也會隨著所處環境的改變而發生顯著變化，如果輸入信號之間的差異特別大，還會導致小數據被大數據淹沒，因此，歸一化處理是數據訓練前必須進行的一項預處理工作，歸一化處理公式為：

(12)

歸一化后的數值yi為網絡的實際輸入值，控制系統實際采集和計算得出的物理量數值用xi表示。

在該模型中對每個輸入變量均設置5個模糊語言變量，即輸入變量在論域內有5個隸屬函數，分別對應5個語言變量，因此該模糊神經網絡共可產生25條控制規則。每條控制規則都對應輸出神經網絡的兩個輸出節點，第四層與第五層的聯接權值即為控制規則中的輸出量[10]。

第一層作為輸入層，x1,x2分別為煅燒溫度和煅燒溫度變化率，該層輸入值直接發送到下一層。第二層每個節點采用式(1)計算與其輸入對應的模糊量隸屬度。兩個輸入節點分別有5個語言變量，故該層的節點個數為10。第三層為模糊神經網絡的規則層，采用式(2)計算每條規則的適用度，該層節點個數為各輸入的語言變量數目的累乘積，即25個。第四層作為模糊神經網絡的歸一層，采用式(3)進行歸一化計算，其總節點數為25。第五層作為模糊神經網絡的規則層，按照式(4)計算輸出結果。

模糊神經網絡輸出值為0～1之間的歸一化值，要對石灰窯煅燒系統進行控制，需要將輸出的天然氣流量和助燃空氣流量的歸一化值向實際控制值轉換，轉換公式為：

Q實際=Qmin+yi×(Qmax-Qmin)

(13)

式中：yi為模糊神經網絡輸出值；Qmax和Qmin為天然氣流量和助燃空氣流量的實際控制范圍的最大最小值。

經過向物理量轉換后可得到石灰窯溫度和溫度變化率處于某種狀態時應設置的最優天然氣流量和助燃空氣流量，使石灰窯煅燒帶溫度維持在最優狀態。

3.2 石灰窯模糊神經網絡學習與訓練

模糊神經網絡算法核心是對網絡連接權值的調整，通過對大量樣本數據的訓練使網絡連接權值不斷改變，直到網絡實際的輸出與期望輸出之間的誤差達到訓練所設定的值時才停止對連接權值的調整。

通過對模糊神經網絡訓練算法公式的推導可以發現，模糊神經網絡模型的建立最主要是找到合適模糊神經網絡的權值，確定各個模糊變量上合適的隸屬度函數的中心值和寬度值，從而使網絡實際輸出與期望輸出盡可能接近。訓練樣本數據參考文獻[11]中的數據，120組用于模糊神經網絡訓練，40組用于驗證模糊神經網絡的學習效果。樣本數據和歸一化數據如表1和表2所示。

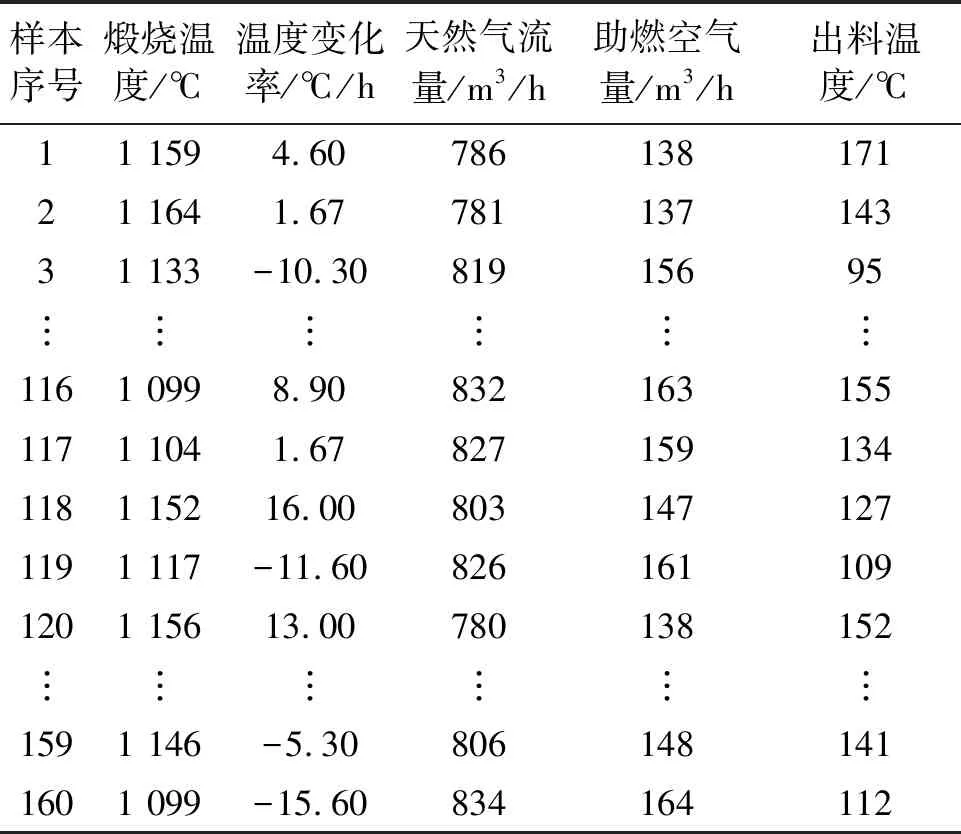
表1 訓練樣本數據

網絡訓練借助 MATLAB 軟件進行，各個節點的輸出均用矩陣運算實現，在開始運算前隨機給定隸屬度中心值、隸屬寬度值和最后一層網絡權值，再運用反向傳播算法根據誤差調整權值、隸屬度函數中心值和寬度值，直至120組樣本輸出數據與實際輸出的總體誤差和小于規定誤差后退出訓練循環并結束程序。樣本總體誤差曲線如圖6所示。

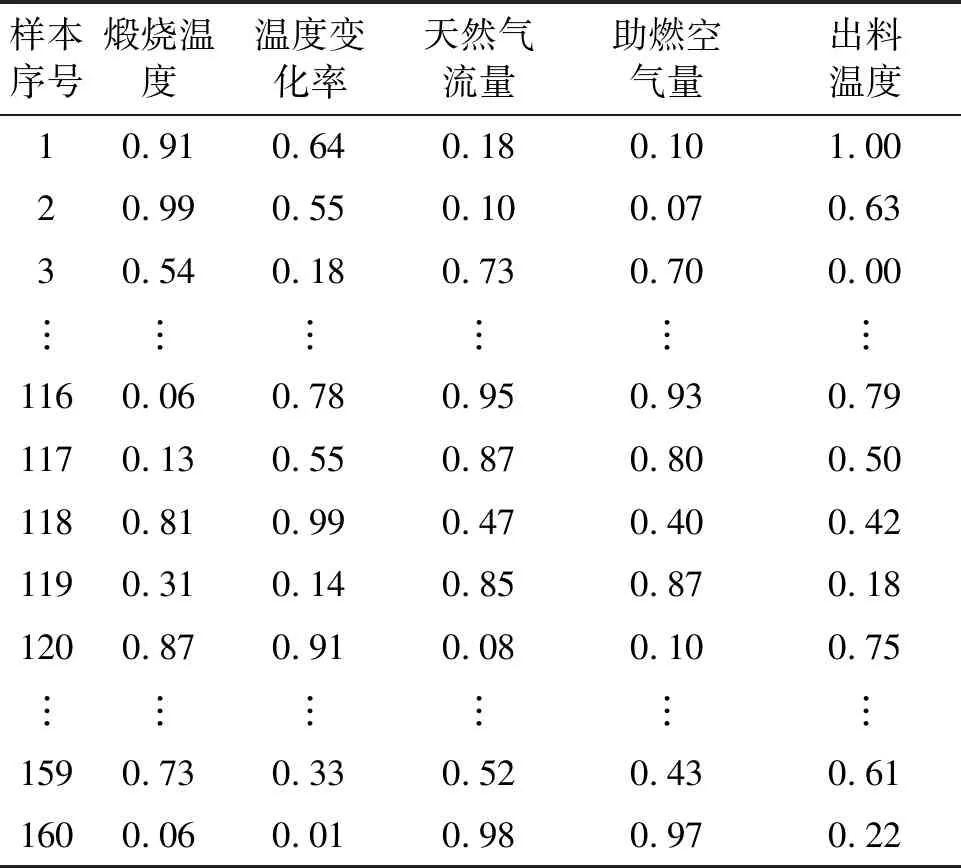
表2 樣本歸一化數據

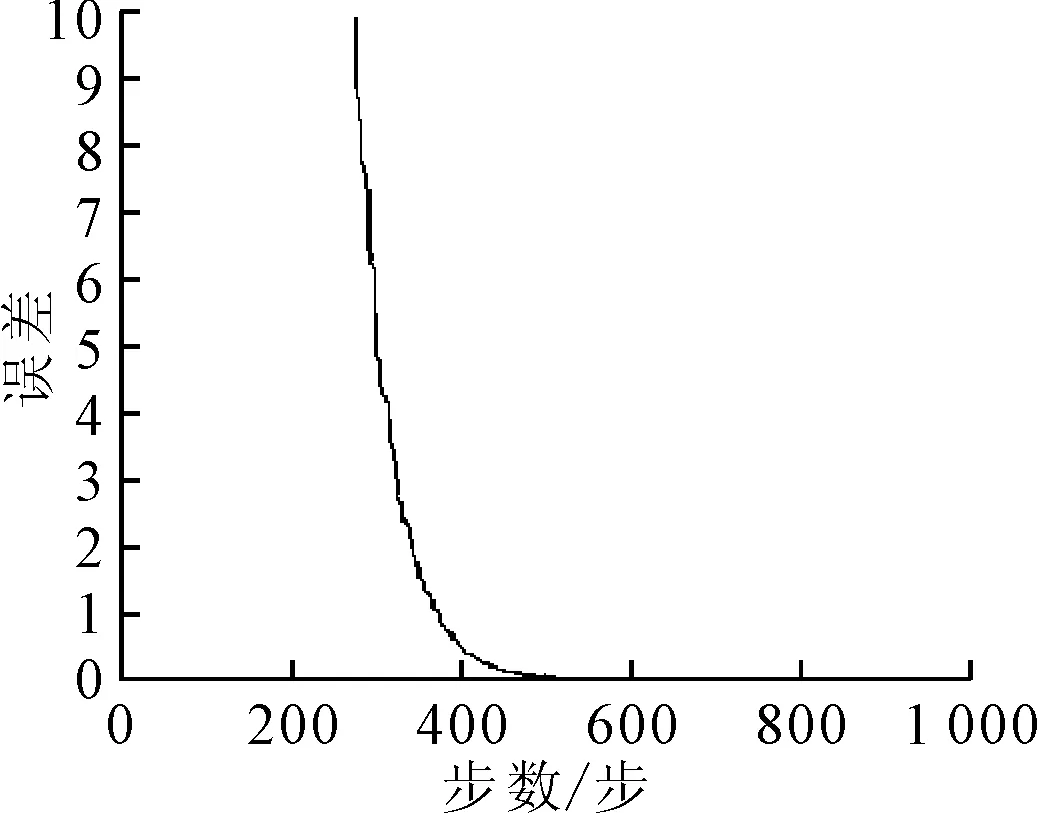
圖6 樣本總體誤差曲線

由圖6可知，在設定最大訓練次數為1 000次的情況下，總體樣本誤差隨著訓練次數的增加逐漸下降，且下降過程中沒有誤差反彈現象出現，驗證了模糊神經網絡學習算法的正確性。

為驗證三葉回轉石灰窯T-S模糊神經網絡能否表達石灰窯的特征，用剩余40個樣本數據的煅燒溫度和溫度變化率作為訓練好的網絡輸入，計算網絡輸出并與樣本數據中的燃氣量和助燃空氣量對比，三葉回轉石灰窯模糊神經網絡的燃氣流量輸出和助燃空氣流量輸出與測試樣本擬合對比如圖7、圖8所示。從圖7和圖8可以看出模糊神經網絡輸出的控制量與樣本數據高度相似，該模糊神經網絡可用于石灰窯DCS(distributed control system)控制系統做控制參數輸出計算。

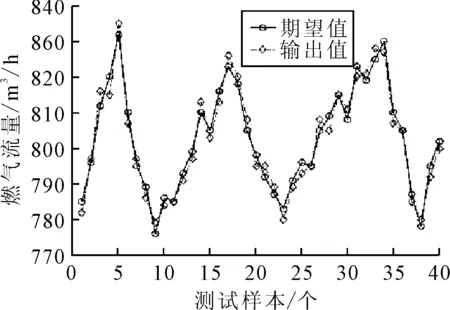
圖7 燃氣流量樣本與網絡輸出擬合對比

圖8 助燃空氣量樣本與網絡輸出擬合對比

3.3 石灰窯模糊神經網絡的應用

石灰窯系統是動態系統，石灰石成分和粒徑變化、流量變化和環境溫度等都會對石灰窯煅燒系統產生影響，若僅用模糊神經網絡充當控制器不能適應石灰窯生產條件的變化，難以保證石灰質量，自校正控制可以彌補這一缺點[12-13]。石灰窯煅燒系統模糊神經網絡自適應控制原理如圖9所示，共有兩條回路，一條為模糊神經網絡學習和優化控制器參數回路，一條為模糊神經網絡控制器和石灰窯煅燒系統組成的反饋控制回路。石灰窯煅燒系統受工況條件影響較大，模糊神經網絡學習模塊根據控制器的輸出和被控系統的實際輸出不斷學習，形成適應工況的模糊控制規則，進而對模糊神經網絡控制器的參數進行優化，控制器根據新的控制參數輸出控制參量可以達到良好的控制效果。

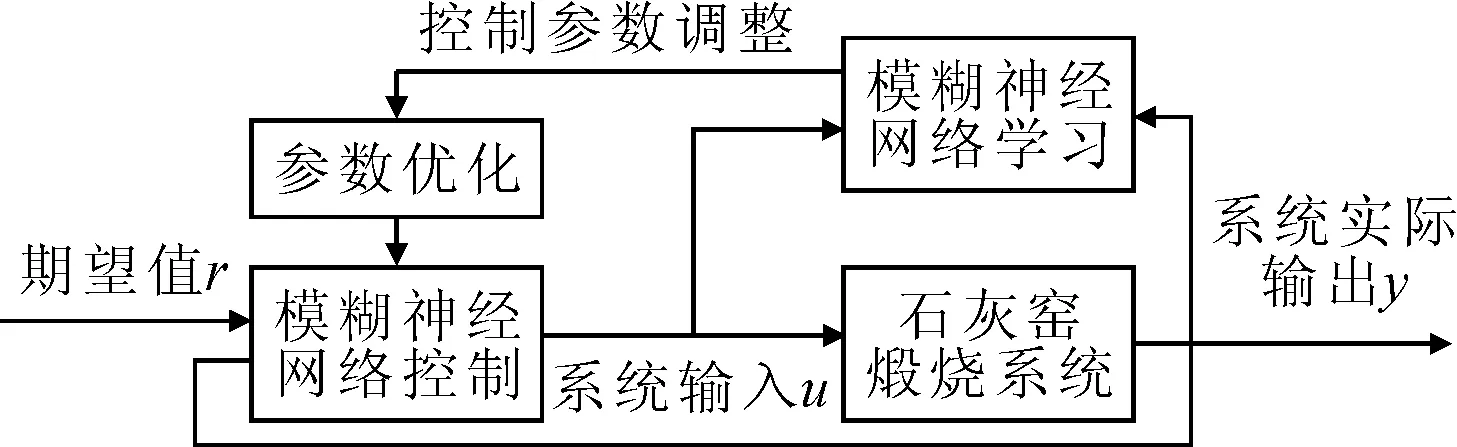
圖9 石灰窯煅燒系統自校正控制原理

4 結論

針對石灰窯煅燒帶溫度難以控制的問題，建立了2個輸入2個輸出的三葉回轉石灰窯的模糊神經網絡模型，用石灰窯在不同工況下的樣本訓練網絡模型，經過誤差反向傳播算法學習后，模型能夠準確表達出石灰窯的特征，證明該模糊神經網絡學習能力強，能夠根據石灰窯溫度和溫度變化率準確計算出石灰窯的控制參數，將該網絡模型參數和算法應用于石灰窯控制系統中能夠有效提高石灰產品的質量。