奇異譜分析在地鐵沉降預測中的應用
王思捷,黃 騰,周立俊,吳壯壯
(1.河海大學 地球科學與工程學院,江蘇 南京 211100)
近年來,城市地下軌道交通飛速發展,緩解了地面交通占地大、人流多、易擁堵的狀況。為了保障地鐵安全運行,必須長期對地鐵軌道實施變形監測工作,及時掌握地鐵的健康狀態,避免惡性事件的發生[1]。隨著地鐵線路的不斷增加,傳統的定期監測手段已不能滿足要求,自動化、智能化監測方法成為地鐵變形監測的主要研究方向[2]。時間序列分析[3]、自回歸模型[4]、GM(1,1)模型[5]、卡爾曼濾波[6]、小波分析[7]、神經網絡[8]等現有方法均取得了一定的成果,但奇異譜分析(SSA)方法在地鐵變形監測方面的研究與應用還較少。
利用沉降監測的時間序列數據進行建模進而對未來一段時間內的沉降量進行預測是當前地鐵沉降預測的主要方案;而當時間序列中含有噪聲時,將大大降低模型的預測精度。SSA方法具有不受正弦波假定的約束、無需先驗信息的優點,可從原序列中提取到盡可能多的可靠信息,從而達到去噪效果[9]。BP神經網絡是一種自適應的預測模型,能對非線性序列在短期內實現很好的預報[10]。本文提出的SSA_BP神經網絡模型,首先利用SSA方法的優越性對原始序列進行分解,提取其中的趨勢項與周期成分,同時削弱噪聲、提高信噪比;然后利用BP神經網絡方法分別對趨勢項與周期成分進行訓練,構建預測模型;最后進行重構預測,得到的趨勢值與周期值即為最終預測結果。
1 SSA方法
對一維時間序列X={xi|i=1,2,...,n}進行SSA,可分為構建軌跡矩陣、奇異值分解和序列重構3個主要步驟[11]。
1)構建軌跡矩陣。首先選擇合適的嵌入窗口長度L(2≤L≤n/2),且有K=n-L+1;再構建一個L×K的軌跡矩陣XL×K,計算公式為:
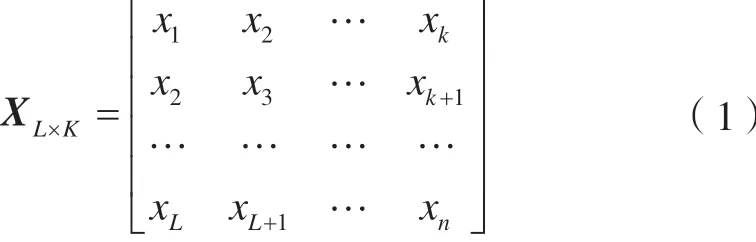
2)奇異值分解。由于式(1)不方便直接求解其特征值和特征向量,因此定義矩陣C=XXT,計算其特征值λi和對應的特征向量Ui,再按特征值降序排列λ1≥λ2≥…≥λL≥0,其中最大的特征值對應的特征向量即為序列的趨勢,一般將較小特征值對應的特征向量當作噪聲[12]。
設d=min{L,K},定義Ui和Vi分別為軌跡矩陣的特征值和左、右特征向量。稱為原序列的奇異譜。令初等矩陣為:

則軌跡矩陣可由d個初等矩陣合成,即
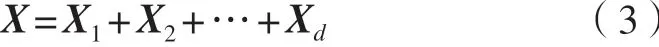
3)序列重構。將第k個時間主分量定義為原序列在UK上的正交投影系數,則有:
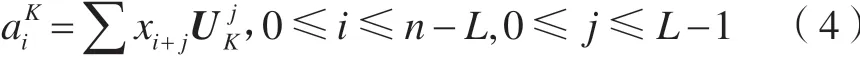
根據UK與VK重構Xi的成分記為xiK,則重構公式為:
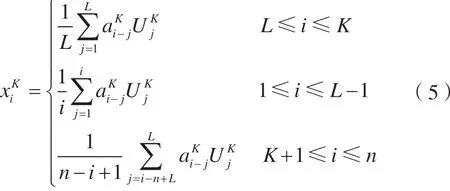
重構成分疊加之和與原序列相同,即

2 SSA_BP神經網絡模型
2.1 BP神經網絡模型
BP神經網絡是一種基于誤差方向傳播算法的前饋網絡,其建模過程主要包括信息正向傳遞和誤差反向傳播。輸入值在輸入層經過帶有權重的隱含層神經元到達輸出層,即為正向傳遞過程;計算實際輸出值與理論輸出值的誤差,并通過反向傳播算法改變隱含層各神經元的權重,即為反向傳播過程。反復迭代正向傳遞與反向傳播,直到輸出值誤差達到期望目標,保存各神經元的權重即可完成模型構建。
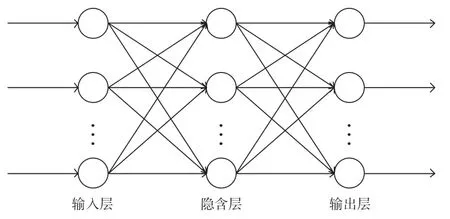
圖1 BP神經網絡結構
2.2 SSA_BP神經網絡模型
本文建立了地鐵沉降的SSA_BP神經網絡模型,首先利用SSA方法處理時間序列的優越性削弱噪聲,并準確提取原始序列的趨勢項與周期成分;然后利用BP神經網絡進行預測并重構,完成模型構建。其具體步驟為:
1)首先對原始序列進行平穩性分析,再利用SSA濾波法確定SSA方法的嵌入窗口長度L和重構階數P。
2)根據Kendall非參數檢驗判斷某個重構成分RCK是否屬于趨勢項,計算滿足xi,K<xj,K的指標數Kr,構造統計量,計算公式為:

假設RCK不是趨勢項,則τ服從均值為0、均方差的正態分布。置信度α=0.05時,若樣本落在(-1.96S,1.96S)區間之外,則拒絕原假設,認為RCK是趨勢項。
3)根據特征值判斷周期成分。若軌跡矩陣的兩個特征值很接近且對應的一對左右特征向量分別正交,則這兩個特征值對應的重構成分之和為原序列的周期成分之一。
4)分別對原序列的趨勢項X1與周期成分X2構建BP神經網絡模型,并預測趨勢值y1與周期值y2。
5)重構趨勢值y1與周期值y2得到實際預測值。
3 實例分析
為了驗證SSA_BP神經網絡模型的正確性和優越性,本文選取某地鐵結構監測區中一個監測點連續44期的實測數據作為樣本,計算原始數據的自相關系數p,并對其進行平穩性分析,計算結果如圖2所示。
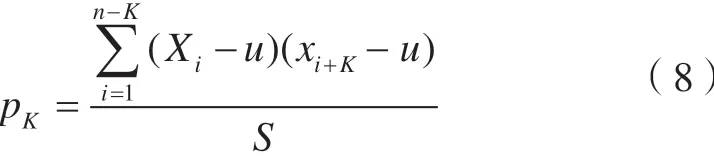
式中,u為序列均值;S為序列方差。
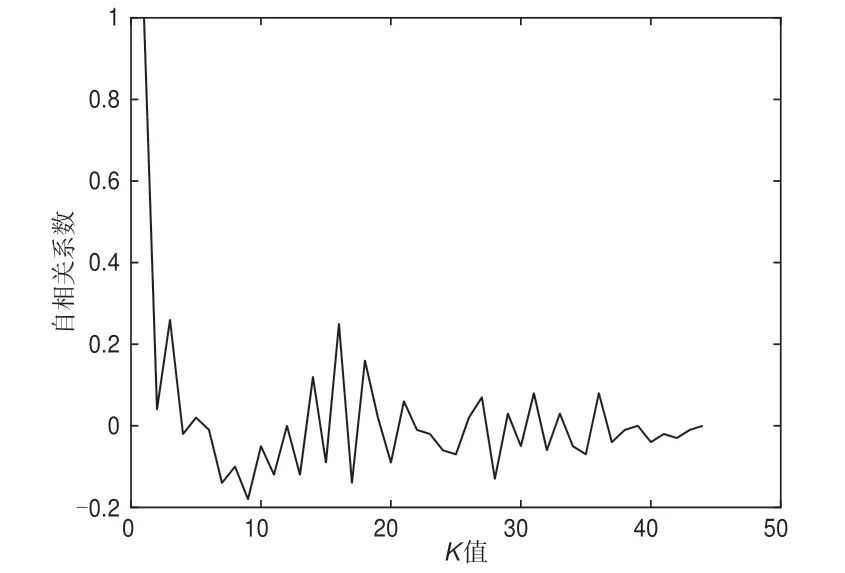
圖2 自相關系數函數圖
由Bartlett理論可知,當xK~N(0,1/44)時,可判斷該序列為平穩序列。pK(K>1)在顯著水平α=0.05條件下的置信區間為(-0.118,0.118),由原始數據的自相關系數可知,p3、p7、p9等9個數落在置信區間之外,因此原始數據為非平穩序列,適合采用SSA方法對其進行處理。利用SSA濾波法確定構建軌跡矩陣的嵌入窗口長度(L=16)和重構階數(P=15)。求出特征值與特征向量后,根據Kendall檢驗與Hurst指數,確定最大特征值對應的重構序列為趨勢項,最小特征值對應的重構序列為噪聲,其余項之和為周期成分。原始數據的趨勢項與周期成分如圖3所示。
將前34期數據分為9個訓練樣本,每個樣本包含26期數據,其中前25期數據作為輸入,最后一期作為輸出數據的期望值。利用訓練樣本分別建立BP神經網絡模型和SSA_BP神經網絡模型,并對35~44期沉降量進行預測。由于神經網絡的預測結果具有不穩定性,因此采用兩種模型分別進行10次預測取均值作為最終預測結果。以實測值與預測值之差的絕對值為殘差,結果如表1所示,可以看出,BP神經網絡模型
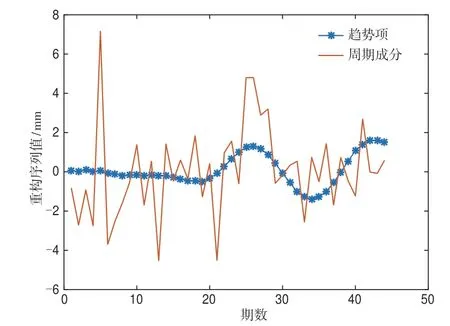
圖3 SSA方法重構序列圖
的預測值殘差最大值達到1.28 mm;而SSA_BP神經網絡模型預測值殘差最大值為0.32 mm,且90%的預測值殘差均優于前者,說明其整體預測精度更高。結合圖4可以看出,BP神經網絡模型在預測第41期時殘差急劇增加,表現出模型只能進行短期有效預測的缺點;而SSA_BP神經網絡模型在全部10期的預測中表現穩定,證明其對于長時間跨度的預測更加可靠。
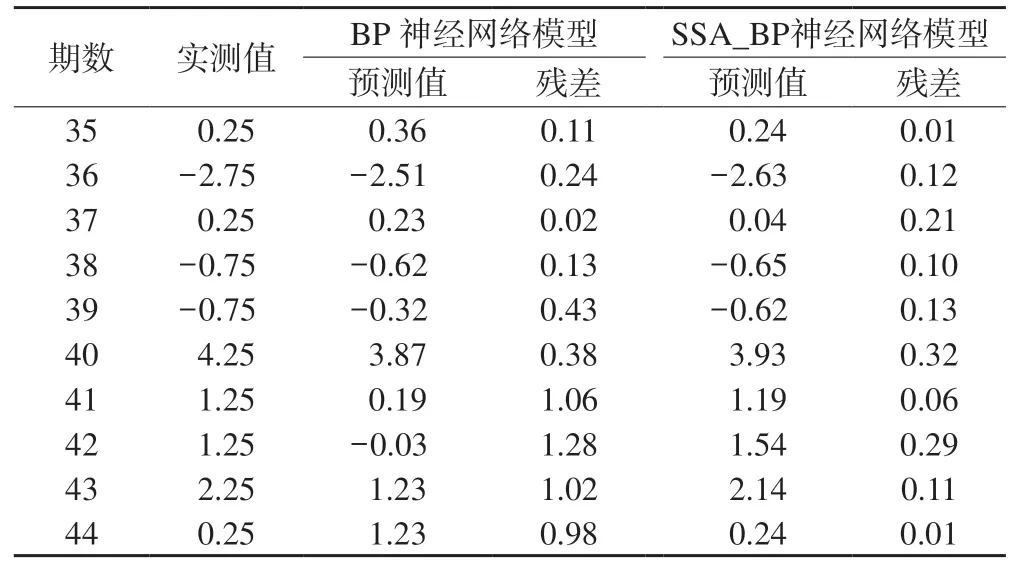
表1 兩種模型預測結果對比/mm
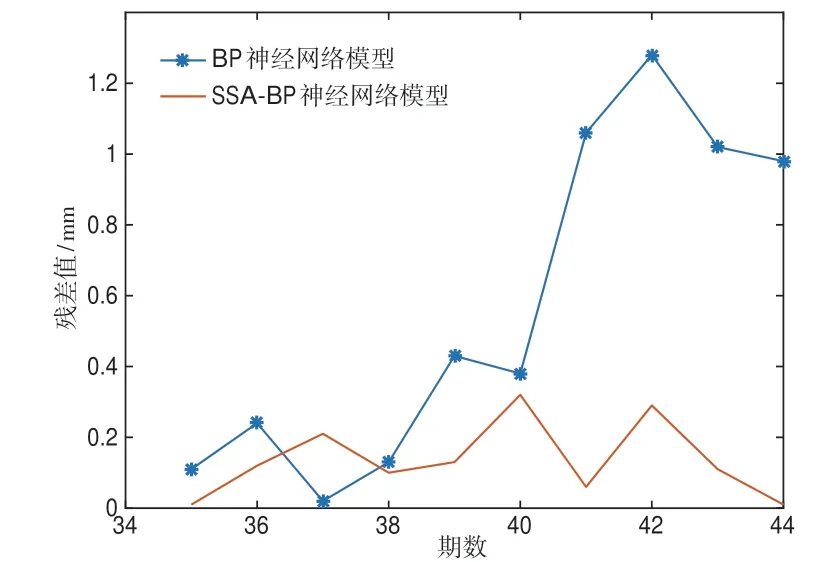
圖4 預測結果殘差對比圖
4 結 語
SSA方法能有效降低數據噪聲對預測模型的干擾,并準確提取趨勢項與周期成分,與BP神經網絡相結合能更好地對非線性數據進行預測。本文通過對比分析BP神經網絡模型與SSA_BP神經網絡模型發現,SSA_BP神經網絡模型充分利用了SSA方法的優勢,采用噪聲更少的數據建立了更優的預測模型,比單一的BP神經網絡模型預測結果精度更高,且預測結果穩定,可應用于地鐵沉降的長期預測。然而,本文的實例分析并不能得出SSA_BP神經網絡模型的最大預測長度,還需對其進行進一步研究。

