基于GA-SVR的地鐵隧道沉降預測

周立俊，黃 騰，王思捷，吳壯壯

（1.河海大學 地球科學與工程學院，江蘇 南京 210000）

為了保障地鐵的安全運營，對隧道結構進行長期的變形監測和預測具有重要意義。由于受到多種隨機性、不確定性因素的影響，地下隧道數據存在非線性、復雜性、多模態性等特點，導致沉降預測存在諸多困難[1]。針對變形預測，許多專家和學者提出了多種模型，如卡爾曼濾波模型、灰色系統理論模型、人工神經網絡模型、回歸分析法等。由于變形量的隨機性和非線性，不同模型的適用性也不同，需對各種模型進行改進和完善。張士勇[2]、姜剛[3]等研究了小波神經網絡模型在地鐵沉降預測中的應用，得出了組合模型比單一預測模型準確度高的結論；高彩云[4]等利用遺傳算法（GA）對地鐵沉降預測模型參數進行了搜索，得出GA能有效獲取極限學習機網絡優化的初始權值和閾值的結論；陳柚州[5]等研究了人工蜂群優化小波神經網絡模型在變形預測中的應用，得出經人工蜂群算法優化后的小波神經網絡模型精度更高的結論。

神經網絡的方法雖然考慮了多種影響因素，但易產生局部最優解；樣本較少時精度較低，樣本較多時易過度學習，導致模型泛化能力較低[6]。支持向量回歸（SVR）能較好地實現小樣本、高維度、非線性的預測，并能有效克服神經網絡陷入局部最優、過學習現象以及對樣本處理依賴經驗等缺點[7]。GA是一種啟發式全局優化算法，具有很好的全局尋優能力[8]。因此，本文利用GA優化SVR模型的參數，從而構建基于GA-SVR的地鐵隧道沉降預測模型，并通過實例驗證了模型的可行性。

1 SVR的原理

SVR是支持向量機（SVM）在回歸問題上的推廣。SVM建立在統計學習理論的基礎上，通過最大化分類間隔控制學習機器的容量，以實現結構風險最小化原則；并通過核函數將樣本從輸入空間映射到高維特征空間，以實現在高維空間中的推廣[9]。

假設對于給定的訓練數據(x1,y1),(x2,y2),…,(xn,yn)∈Rn×R，通過一個非線性映射φ將數據映射到高維特征空間，從而將非線性回歸轉化為高維特征空間的線性問題，即

式中，φ(x)為將樣本點映射到高維空間的非線性變換；w為權值矢量；b為閾值。

引入不敏感損失函數ε作為損失函數，定義為：

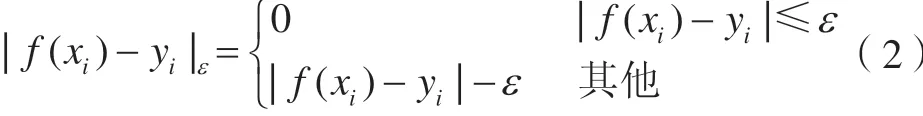
引入非負松弛變量ξi、ξi*，并綜合考慮擬合誤差，可得到線性回歸估計的優化問題，即為訓

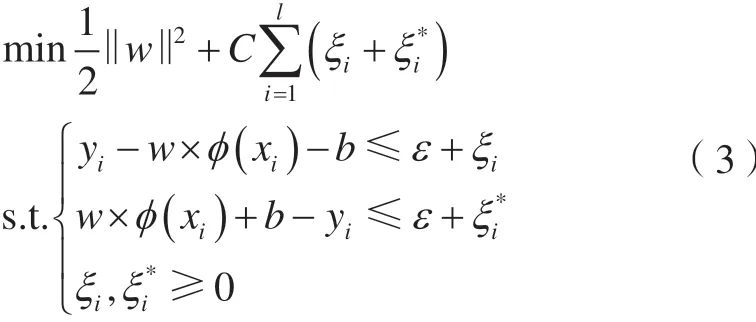
引入拉格朗日函數，并對拉格朗日函數求鞍點，可得該優化問題的對偶問題，即

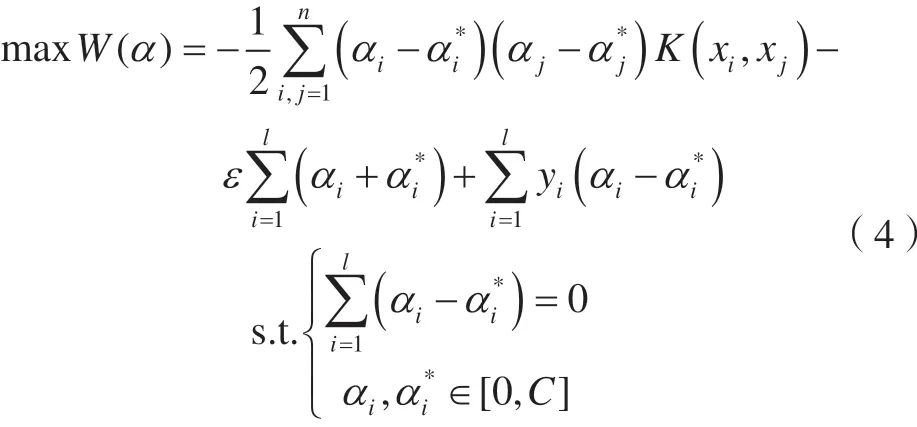
通過引入核函數，可無需知道從低維輸入空間到高維特征空間非線性映射φ(x)的具體形式，而利用原空間中的核函數實現高維空間中要進行的計算，從而得到對應的決策函數。

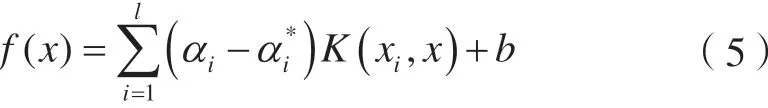
常用的核函數包括多項式核函數、徑向基核函數和Sigmoid核函數，本文選用徑向基核函數，表達式為：

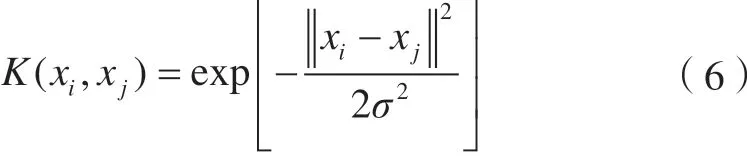
式中，σ為核函數參數，為簡便計算，令γ=1/2σ2。

SVR 模型的預測效果依賴于其模型參數（懲罰參數C、核函數參數γ、不敏感損失函數參數ε等）的選擇[10]。

2 GA-SVR模型

GA是一種模擬生物在自然界中的遺傳機制和進化過程而形成的自適應全局搜索最優解的算法，具有良好的并行性、魯棒性和全局最優性[11]。因此，本文利用GA優化SVR模型的參數，從而構建基于GA-SVR的地鐵隧道沉降預測模型。

GA尋優的具體參數設定：種群個數為100，最大進化代數為200，C的搜索范圍為[0,100]，γ的搜索范圍為[0,100]，ε的搜索范圍為[0,1]。采用間接二進制編碼，每條染色體長度為54個基因，設置交叉概率為0.8，變異概率為0.01。GA參數尋優的具體步驟（圖1）為：

1）初始化種群。隨機產生100個長度為54個基因的染色體（每個基因由0或1構成），前20個基因表示C的搜索范圍，中間20個基因表示γ的搜索范圍，最后14個基因表示ε的搜索范圍。

2）計算各染色體的適應度。以訓練樣本的留一交叉驗證結果生成的均方誤差（MSE）的均值作為適應度函數，表達式為：

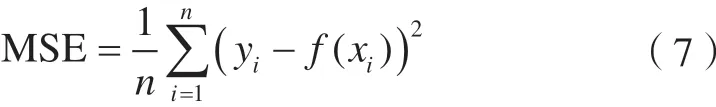
式中，i為樣本個數；xi為參考模型的實際值；f(xi)為通過SVM計算得到的預測值。

3）選擇操作采用輪盤賭的方式，即適應度越大的染色體被選中的概率越大。

4）交叉操作采用單點交叉的方式，即在染色體中隨機選定一個交叉點，發生交叉的兩條染色體在該點前后進行部分互換，以產生新的個體。

5）變異操作。由于是二進制編碼，隨機選擇發生變異的基因，該基因若為0，則變異為1；反之，則變異為0。

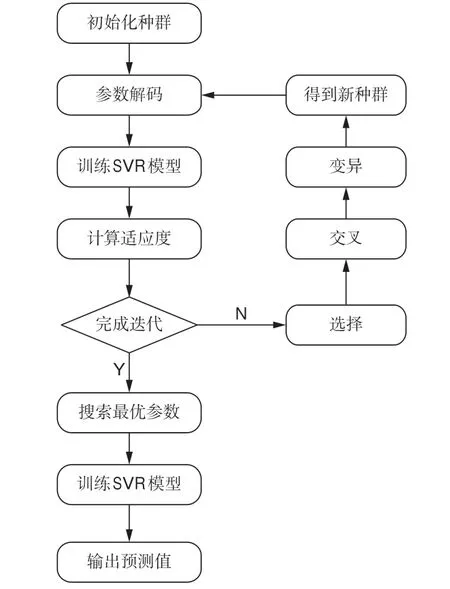
圖1 GA參數尋優流程圖

3 工程實例應用與分析

本文以南京地鐵2號線漢油段的結構監測項目為例，該段隧道全長12.026 km；沉降監測高程系統采用吳淞高程系，設有沉降監測點1 200余個，其中包括3個控制網基準點和11個工作基點；采用嚴密平差的方法，按距離倒數定權，平差由科傻系統自動進行水準閉合差計算、平差、精度評定以及成果表格的輸出。目前，該項目的垂直位移監測已進行36期，歷時9 a，每3個月一期。本文選取莫愁湖至漢中門上行隧道內某點的全部36期高程觀測數據，將前31期分為21個訓練樣本，每個訓練樣本中有11期觀測數據，前10期作為輸入，11期作為前10期的標簽；訓練結束后，對后5期進行預測。根據上述算法和實例應用，基于Python語言，在Jupyter Notebook環境下，調用Scikitlearn中的SVR工具箱編寫GA-SVR程序。

GA參數尋優過程如圖2所示，可以看出，經過150次迭代后基本達到最優，迭代200次后終止，GA優化后C=1.135 83，γ=0.011 92，ε=0.001 95。將尋優所得的參數代入SVR模型對樣本訓練集進行訓練，訓練后各訓練樣本的預測值與實測值具有很好的擬合度，如圖3所示。訓練集的預測值與實測值的最小絕對誤差為-0.002 mm，最大絕對誤差為3.00 mm，絕對誤差平均值為0.12 mm，訓練集的樣本MSE為1.63 mm2。

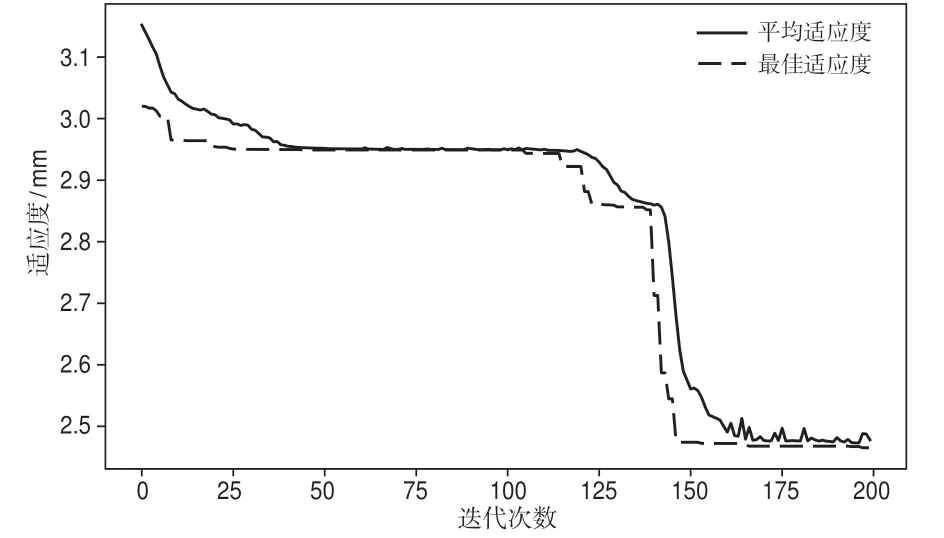
圖2 GA參數尋優過程

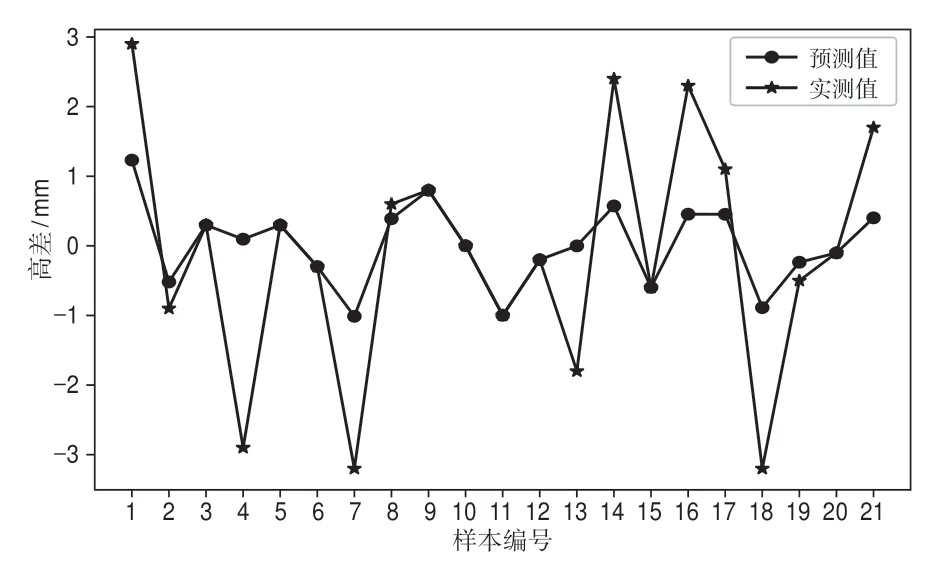
圖3 訓練樣本預測結果對比

利用訓練好的SVR模型對測試集樣本進行預測，結果如圖4所示。預測值與實測值的最小絕對誤差為0.02 mm，最大絕對誤差為1.22 mm，絕對誤差平均值為0.38 mm，測試集的樣本MSE為0.43 mm2。結果表明，基于GA-SVR的地鐵隧道沉降預測具有一定的實用性，其精度能滿足實際工程要求。

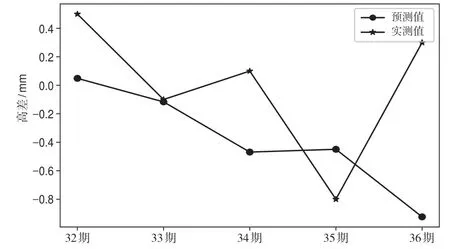
圖4 測試樣本預測結果對比

4 結 語

地鐵隧道沉降受眾多隨機、不確定因素影響，監測數據存在非線性、復雜性等特點。基于結構風險最小化的SVR模型能很好地解決在擬合地鐵隧道沉降數據時出現的隨機性、非線性等問題；但SVR模型的擬合效果依賴于模型中3個參數。GA作為自適應全局搜索最優解的算法，在SVR模型的最佳參數組合方面表現出優異的搜索性能。本文從時間序列的角度對地鐵隧道沉降進行了預測，構建的GA-SVR模型能對地鐵隧道沉降變形進行較為準確的預測，其精度能滿足工程實際要求。