縫合復合材料T型接頭拉伸載荷下的有限元數值模擬

文立偉，余坤，宦華松

南京航空航天大學 材料科學與技術學院，南京 210016

縫合復合材料T型接頭在拉伸載荷下，接頭筋條與蒙皮變形程度較大，縫線受力情況復雜，使得T型接頭失效機理分析較為復雜[1-2]。近年來，國內外學者通過理論[3]、試驗[4]及數值模擬[5]的方法針對復合材料縫合件進行了廣泛研究。

縫合的應用最早是為解決層合板的分層問題，20世紀80年代，Mignery等[6]將碳纖維縫入了層合板，結果顯著提高了層合板的層間強度，提高了層合板厚度方向的承力作用。Velmurugan和Solaimurugan[7]研究了縫合與未縫合玻璃纖維增強復合材料的層間斷裂韌性以及面內纖維取向對I型層間斷裂韌性的影響。朱華東等[8]研究了縫合密度和縫線直徑對縫合復合材料層合板 Ⅱ 型層間斷裂韌性和分層模式的影響。目前，簡單縫合層合板的研究已相當成熟，在縫合層合板的基礎上，縫合T型接頭將上部筋條與下部蒙皮連接起來，不僅要考慮鋪層層間性能，還要考慮筋條-蒙皮連接界面的界面性能。張國利等[9]在試驗研究BS3-94-10型環氧樹脂性能和縫合件層間剪切和彎曲性能的基礎上，優化設計了樹脂膜融滲技術和縫合工藝參數，制備了高性能T型加筋壁板試樣。經測試，縫合后T型加筋整體壁板平均臨界屈曲強力、平均破壞強力、正面和背面相同位置上最大破壞應變分別增加24.6%、18.3%、21.2%和24.6%。此外，Kim等[10]采用一種新的單線縫合工藝制備T形接頭，使碳纖維的彎曲程度最小化并防止其斷裂。拉伸試驗結果表明：縫合纖維密度為0.5%和2%的T型接頭的破壞載荷相比未縫合試樣提高40.56%～47.47%，并且高于相同增強纖維密度下的Z-pin試樣。當前，國內外關于縫合復合材料的數值模擬研究，主要集中于縫合層合板。葉強和陳普會[11]從復合材料的細觀結構出發，提出了用于預測粘聚區模型的強度參數的細觀模型, 以提高有限元法模擬復合材料分層的精度。孔斌等[12]利用三維有限元模型研究了Z-pin/縫合增強試驗件的剪切承載能力，指出應選擇拉伸強度較高而拉伸模量較低的縫線來進行縫合增強設計。Iwahori等[13]利用二維有限元模擬了縫合層合板和三維正交互鎖織物的雙懸臂梁(DCB)試驗結果，建立了這2種復合材料分層擴展的力學模型。針對復合材料T型接頭的仿真研究多見諸于Z-pin增強件，李夢佳等[14]建立了Z-pin增強T型接頭的二維平面應變模型，研究了Z-pin參數對T型接頭拉伸性能的影響。Grassi和Zhang[15]在DCB模型中,將Z-pin模擬成只連接上下懸臂梁膠接界面的非線性界面元，發現當脫膠擴展至Z-pin布置區域后，Z-pin能有效地抑制脫膠。

以往的研究更加關注縫合層合板的力學性能[16-18]，而復合材料T型結構受自身形狀以及筋條-蒙皮間連接界面的影響，在外部載荷下的受力情況與損傷失效行為更加復雜[19]。當前針對縫合T型接頭的研究又大多集中于試驗分析，極少涉及參數化的數值模擬。本文利用ABAQUS有限元軟件對拉伸載荷下的縫合T型接頭進行了建模與分析，通過對比有限元結果與試驗值，驗證了分析方法的可靠性。在此基礎上，對縫線進行參數化分析，研究縫合參數對T型接頭拉脫承載能力的影響，總結縫線增強規律。研究結果對復合材料T型接頭的縫合增強設計具有一定的指導意義。

1 建 模

1.1 材料與試驗

縫合T型接頭試樣的幾何尺寸如圖1所示，寬度為40 mm，結構由蒙皮、兩片筋條及填充物組成。筋條鋪層為[0/90]2S，厚度為1 mm；蒙皮鋪層為[0/90]4S，厚度為2 mm。結構采用T700/RTM 3312A復合材料，填充區(R區)材料與主體結構相同，材料性能如表1所示。筋條與蒙皮連接區域為縫合區，縫線為Kevlar-29纖維，性能見表2。實驗加載速率為0.5 mm/min，加載跨距為120 mm，拉伸試驗加載裝置如圖2所示。

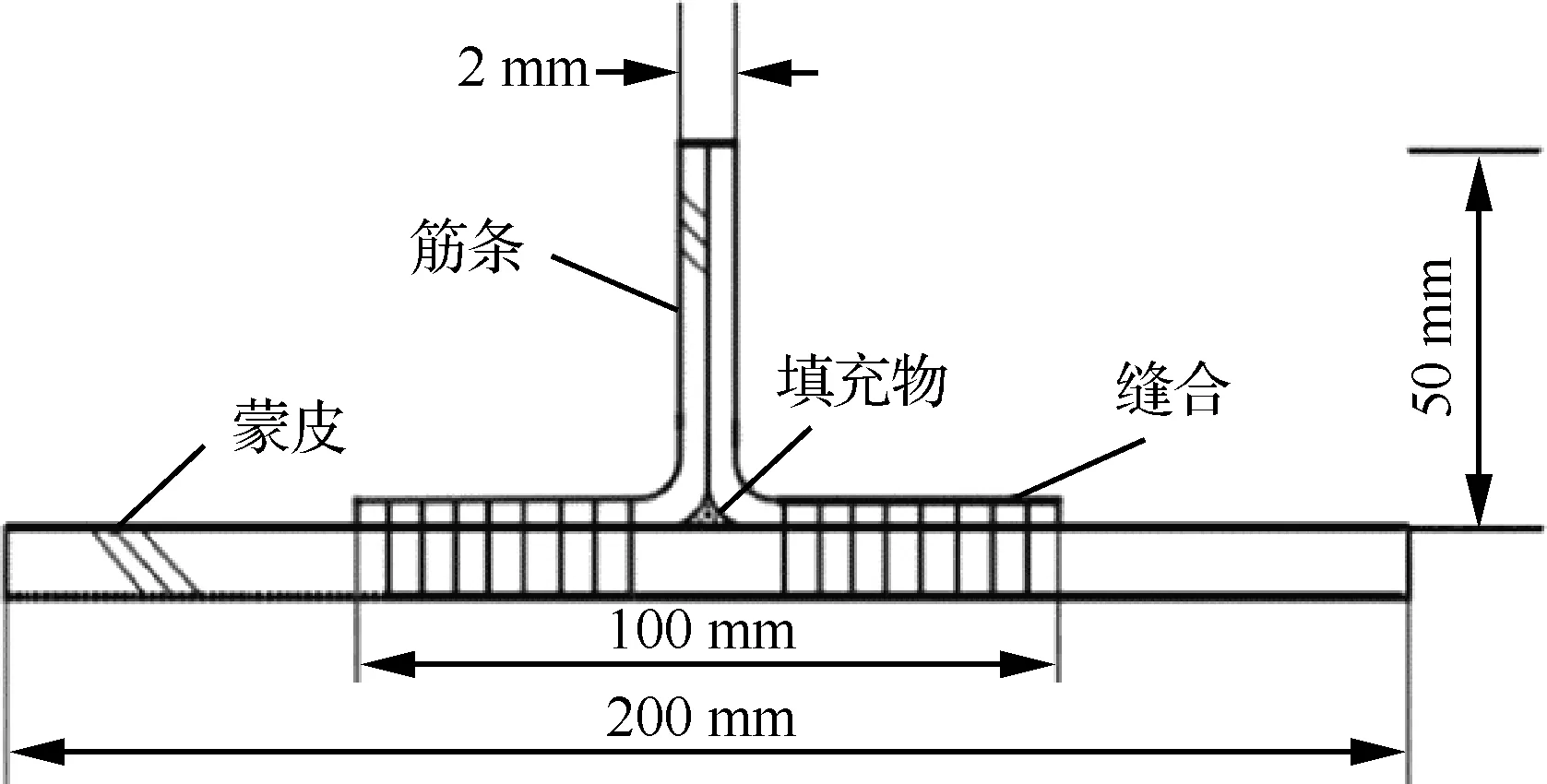
圖1 縫合T型接頭試樣幾何構型Fig.1 Geometry of stitched T-joint sample

表1 T700/RTM3312A復合材料的力學性能Table 1 Mechanical properties of T700/RTM3312A

表2 Kevlar-29縫線力學性能Table 2 Mechanical properties of Kevlar-29

圖2 拉伸試驗加載示意圖Fig.2 Schematic of loading of tensile test

1.2 基于內聚力模型的界面模擬方法

內聚力模型(Cohesive Zone Model, CZM)是對復合材料界面行為的簡化。黏聚接觸行為(Cohesive Behavior)基于內聚力模型，通過定義破壞準則模擬裂紋萌生和擴展，能清楚表現損傷起始和分層擴展，其參數包括能量釋放率、界面強度和界面剛度值等力學特征。本文采用雙線性內聚應力-相對位移(Traction-Separation，T-S)關系，如圖3[20]所示。圖中，K為剛度，τ0為單元失效強度，Δf為失效位移，Δ0為發生初始破壞時的位移，GC為單元臨界能量釋放率(即斷裂韌性)，D為單元損傷系數，當D=1時，單元出現損傷。

圖3 內聚力雙線性本構模型[20]Fig.3 Bi-linear constitutive model of cohesion[20]

T型接頭筋條-蒙皮連接界面在裂紋的演化及失效過程中受 I/Ⅱ 型混合應力[21-22]，因此界面的損傷破壞準則采用BK(Benzeggagh-Kenane)混合準則：

(1)

(2)

式中：GⅠC、GⅡC分別為 I、Ⅱ型臨界應變能釋放率；GⅠ、GⅡ分別為 I、Ⅱ型斷裂應變能釋放率；η為損傷因子，一般在0.5～3之間，本文取2。

1.3 縫線橋聯律

縫線的橋聯律即分層處橋聯力T和相對位移δ之間的關系，縫線在層間作用時，不僅會產生法向拉伸變形，還會受到剪切作用，發生橫向變形。圖4所示是縫線在基體內的變形拔脫圖。當縫線被拉伸到層合板的表面時，由于縫線受到底部縫線的拉扯作用，縫線不會立刻離開表面，此時橋連力T也會繼續增大直到縫線斷裂。當縫線在界面斷裂，會出現急劇掉載，隨后剩余縫線開始被拔出；當縫線在裂紋處斷裂，縫線急劇掉載到零。

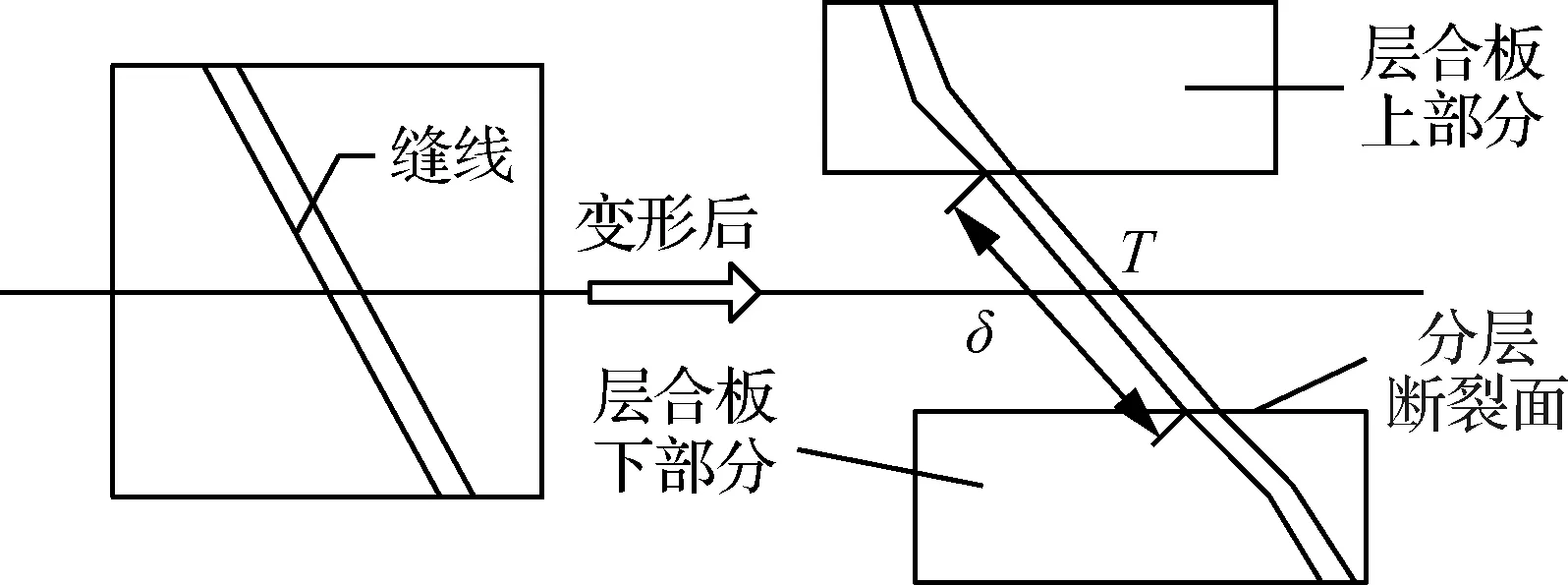
圖4 縫線在層間受力示意圖Fig.4 Stress diagram of thread between layers

縫線直徑不同，其橋聯律也不同。縫線直徑通常用“旦尼爾(Denier)”來表征，指9 000 m長的纖維在公定回潮率時的質量克數，單位為旦(D)，D值越大表示縫線越粗。Kevlar-29縫線的橋聯律通過細觀力學法計算得到，如圖5所示。

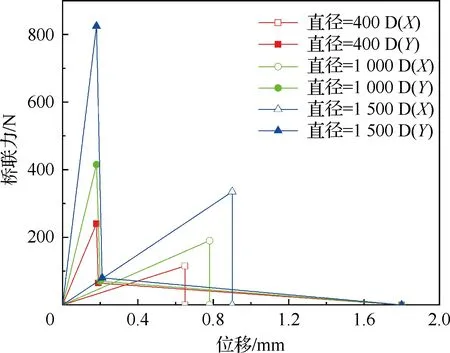
圖5 縫線的橋聯律Fig.5 Bridging law of thread

2 未縫合T型接頭三維模型分析

根據T型接頭實際尺寸建立三維模型，結合夾具夾持位置，將立筋高度取為35 mm，蒙皮長度取為120 mm，寬度不變仍為40 mm。將蒙皮兩端固定，筋條上端施加位移載荷，蒙皮兩端約束U1、U2、U3自由度，以防止蒙皮在拉伸過程中發生移動。并同時約束筋條X方向位移，保證筋條在拉伸過程中不會偏離中心，如圖6(a)所示。兩根筋條和蒙皮采用C3D8I單元，即8節點六面體單元；R區采用C3D6單元，R區受力復雜，承受應力較大，故適當細化網格。模型網格劃分如圖6(b)所示。在接觸面定義表3所示黏聚接觸來模擬蒙皮、筋條和R區接觸界面的界面損傷行為。

圖6 T型接頭三維有限元模型Fig.6 3D finite element model of T-joint

表3 未縫合T型接頭界面黏聚接觸參數定義

未縫合T型接頭有限元計算結果如表4所示。該模型在拉伸載荷下，極限破壞載荷為1 190.20 N， 與試驗值相對誤差為8.2%。初始失效載荷為940.41 N，與試驗值相對誤差為5.9%。 誤差范圍在可接受范圍內，有限元模擬結果與實際試驗吻合。

圖7為未縫合T型接頭三維模型模擬計算得到的載荷-位移曲線，在R區出現裂紋之后，即出現第一次掉載，隨后裂紋沿著筋條向兩邊擴散，在載荷達到極限后不再繼續增加，直到筋條完全脫離蒙皮。曲線基本形狀與試驗結果匹配較好，第一次掉載位移都在5～6 mm之間，極限失效載荷也與試驗值較吻合。且模型的剛度線性段在試驗范圍內，說明有限元的建模、邊界條件及接觸屬性比較符合真實情況，基于內聚力模型(CZM)的黏聚接觸方法來模擬筋條與蒙皮的脫粘行為具有可行性。

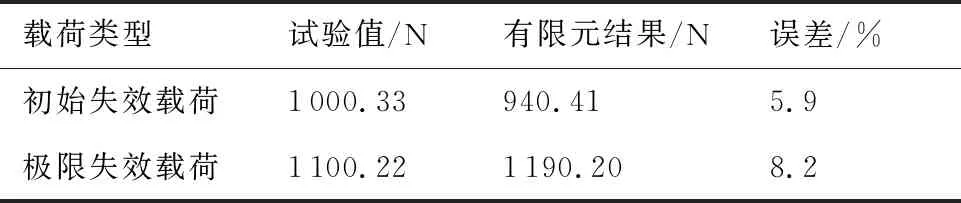
表4 三維模型計算結果Table 4 Calculation results of 3D model

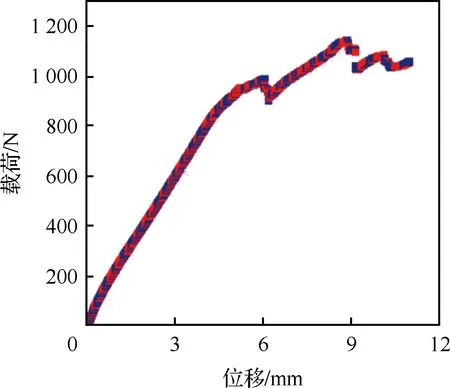
圖7 未縫合T型接頭模型的載荷-位移曲線Fig.7 Load-displacement curve of unstitched T-joint model

3 縫合T型接頭二維模型分析

T型接頭三維有限元模型能較好模擬出真實試驗情況下T型接頭的拉脫性能以及破壞機理。但是三維模型計算量大，模擬時間長，不適合進行參數化分析。為了提高模擬分析效率，嘗試簡化模型。由于T型接頭進行拉伸時，主要是 Ⅰ 型和 Ⅱ 型破壞，Ⅲ 型可以忽略不計[23]，因此建立二維有限元模型進行模擬分析，如圖8所示。

筋條和蒙皮采用CPE4R單元，即四節點平面應變四邊形單元；R區采用CPE3單元。通過在突緣與蒙皮界面相應節點建立非線性彈簧來模擬縫合密度(行距×列距)為10 mm×10 mm的Kevlar-29縫線的增強作用。X方向彈簧模擬界面抗剪切作用，Y方向彈簧模擬界面抗拉脫作用，如圖9所示。縫線的橋聯律圖5已給出。筋條-蒙皮界面參數取為10 mm×10 mm縫合密度的縫合復合材料界面性能，為試驗測算而得均勻等效值，見表5。

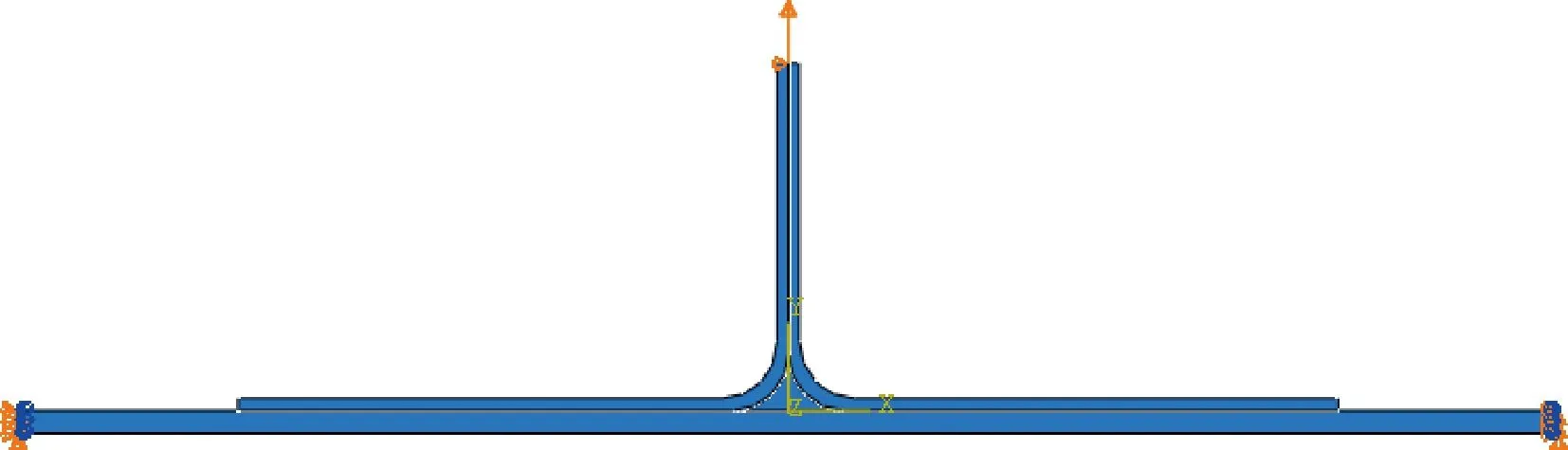
圖8 T型接頭二維有限元模型Fig.8 2D finite element model of T-joint

圖10所示為縫合T型接頭實際拉伸試驗與模擬失效云圖對比，兩者失效形式相似。

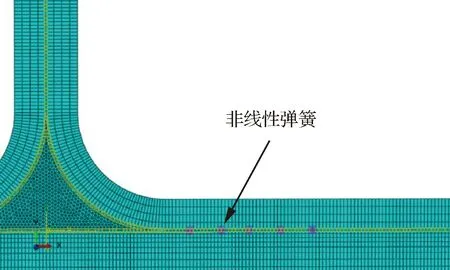
圖9 非線性彈簧模擬縫線Fig.9 Simulation of thread with non-linear spring

表5 縫合T型接頭二維模型界面參數定義Table 5 Interfacial parameters of 2D model of T-joint

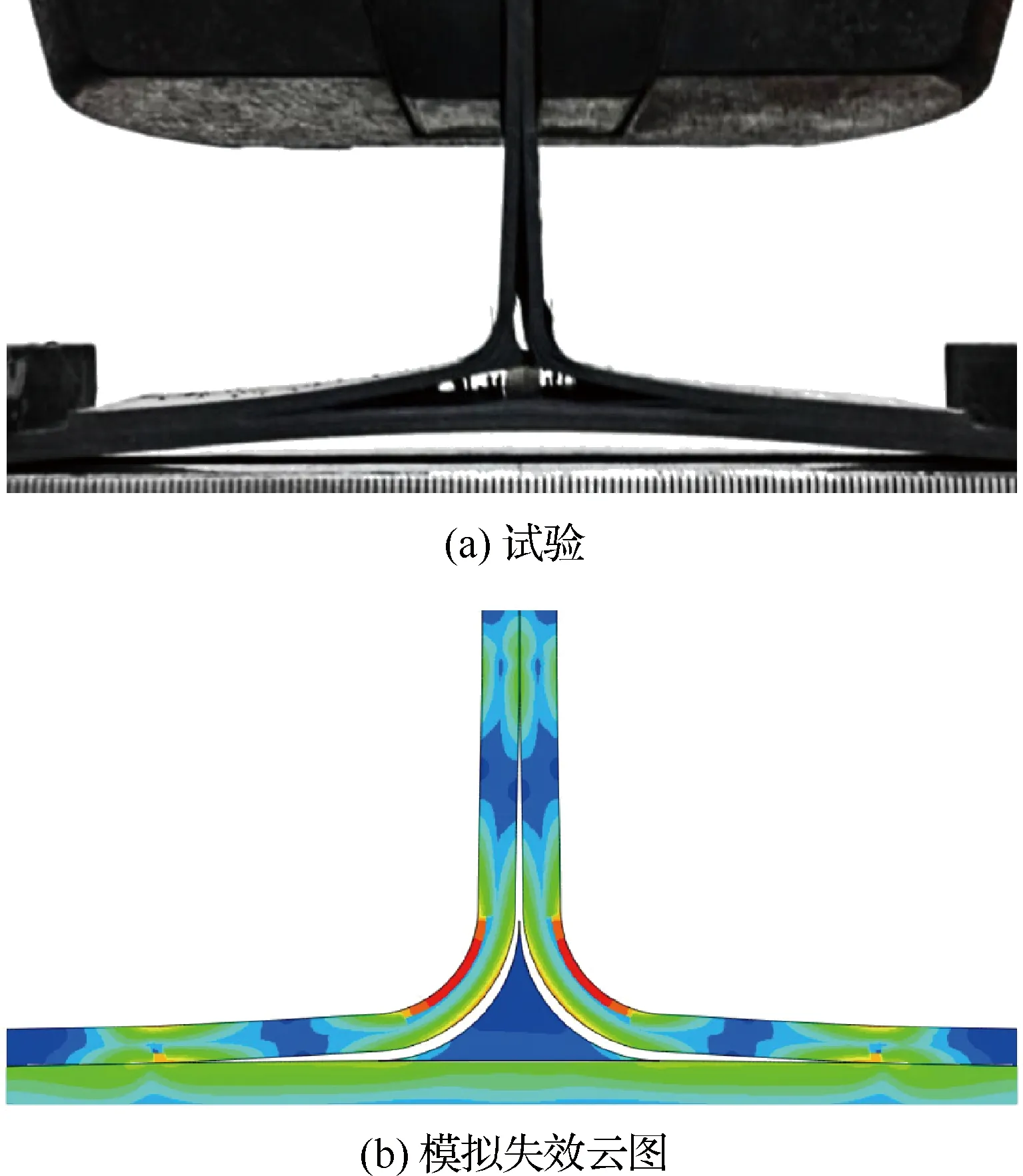
圖10 拉伸試驗與模擬失效云圖對比Fig.10 Comparison between tensile test and simulation

圖11為有限元模擬得到的縫合T型接頭界面失效機制，其中CSDMG表示黏聚接觸界面的剛度退化程度，CSDMG值越大表示界面損傷越嚴重，CSDMG=0表示界面完好無損，CSDMG=1表示界面已完全破壞。有限元結果顯示，在拉伸載荷作用下, 損傷首先出現在緣條與R區的界面 (圖11(a))，繼續加載至結構掉載，緣條與蒙皮間的損傷已大面積擴展(圖11(b))，最終破壞時縫線被拉斷或拔出，筋條與蒙皮完全分離(圖11(c))。縫合不會改變結構的破壞模式，有限元預測的失效機制與試驗觀察基本一致。

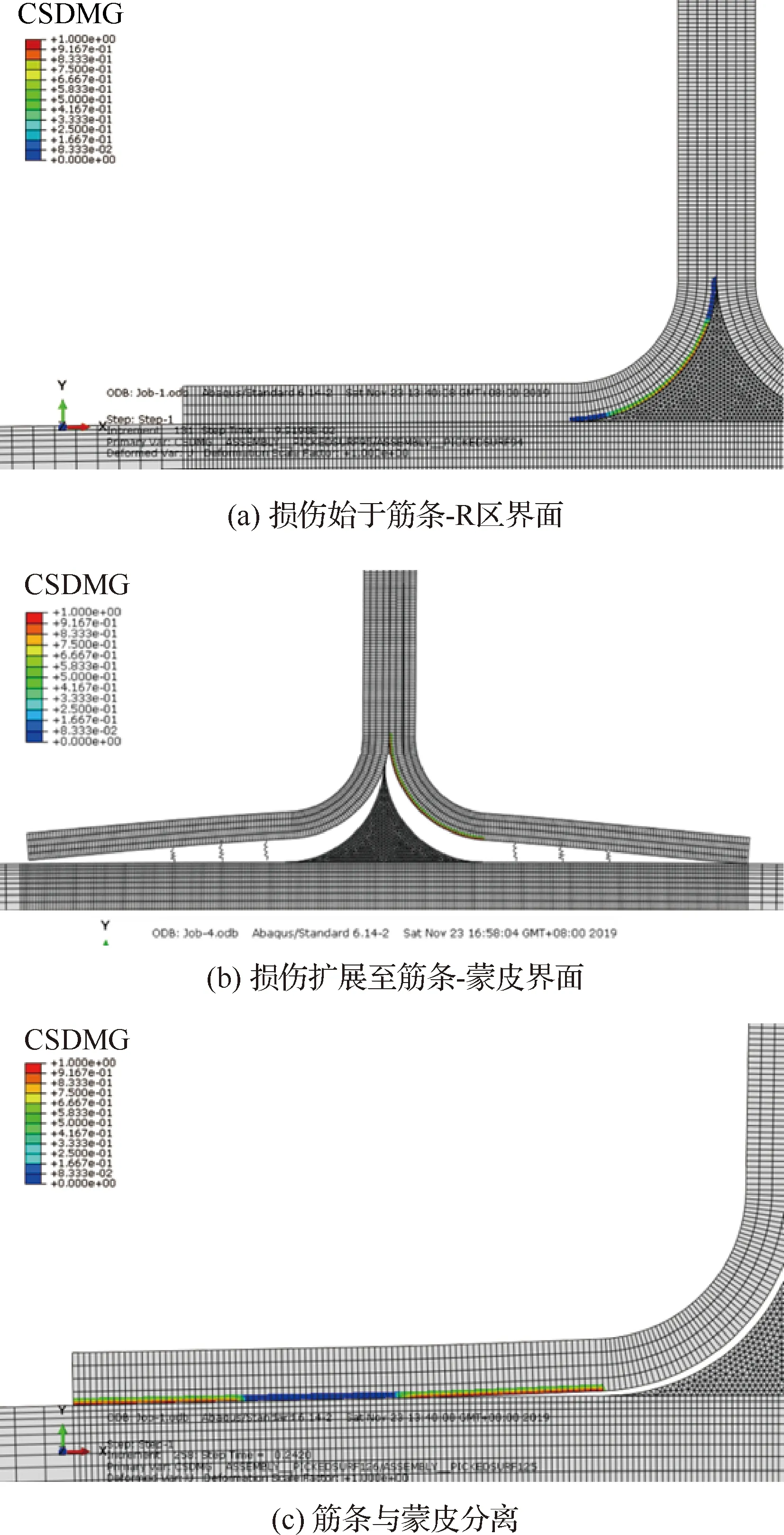
圖11 有限元模擬得到的縫合T型接頭界面失效機制Fig.11 Interface failure mechanism of stitched T-joint simulated by finite element model

在相同的跨距下，分別對未縫合和縫合二維模型進行有限元拉伸模擬，其中縫合二維模型中分別采用直徑400 D、1 000 D和1 500 D的縫線。在有限元中縫線直徑體現在非線性彈簧的拉伸強度及橋聯律的變化。圖12為有限元模擬T型接頭拉伸驗載荷-位移曲線。

由圖12可見，縫合的T型接頭的第1次掉載被延后，并且初始失效載荷都高于未縫合模型，這是因為縫合試樣中的裂紋擴展受到縫線的阻礙作用，相對于未縫合試樣裂紋擴展要緩慢一些。界面裂紋擴展機制如圖13所示，在裂紋擴展初期，拉伸載荷線性增長，當載荷增加到一定程度時，裂紋突然擴展，穿越第1排縫線；在裂紋繼續向第2排縫線擴展過程中，當第1排縫線形成的橋連區域達到飽合且不足以承受施加的載荷時，第1排部分縫線發生斷裂，載荷在此時有一個突降的表現，之后每次載荷突降現象的出現都伴隨部分橋連縫線的斷裂。與未縫合試樣相比，縫合試樣載荷波動較為劇烈，橋聯區域從出現到飽和，載荷基本保持線性增長，當橋連區域達到飽和，部分縫線斷裂，載荷急劇下降，之后又形成新的橋連區域，橋聯區域經歷“形成-飽和-失效-新橋聯區域的形成”這樣幾個階段。

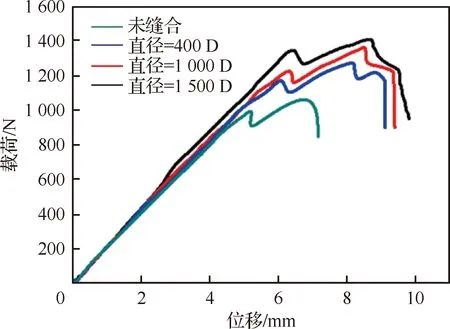
圖12 縫合與未縫合T型接頭模型載荷-位移曲線Fig.12 Load-displacement curves of stitched and unstitched T-joints

有限元模擬分析結果中，隨著縫線直徑增加，T型接頭拉伸承載力增加，原因是縫線變粗，縫線的橋聯力變大，拉伸強度增大，T型接頭抵抗拉脫失效的能力提高。值得注意的是，在實際試驗中，當縫線直徑達到1 500 D時，試樣的極限破壞載荷相比1 000 D縫合試樣并未提高(表6)，原因是有限元模擬分析中未考慮實際情況下縫線可能造成的層合板面內損傷，從而表現為縫線越粗，縫合T型接頭的拉伸承載力越高。

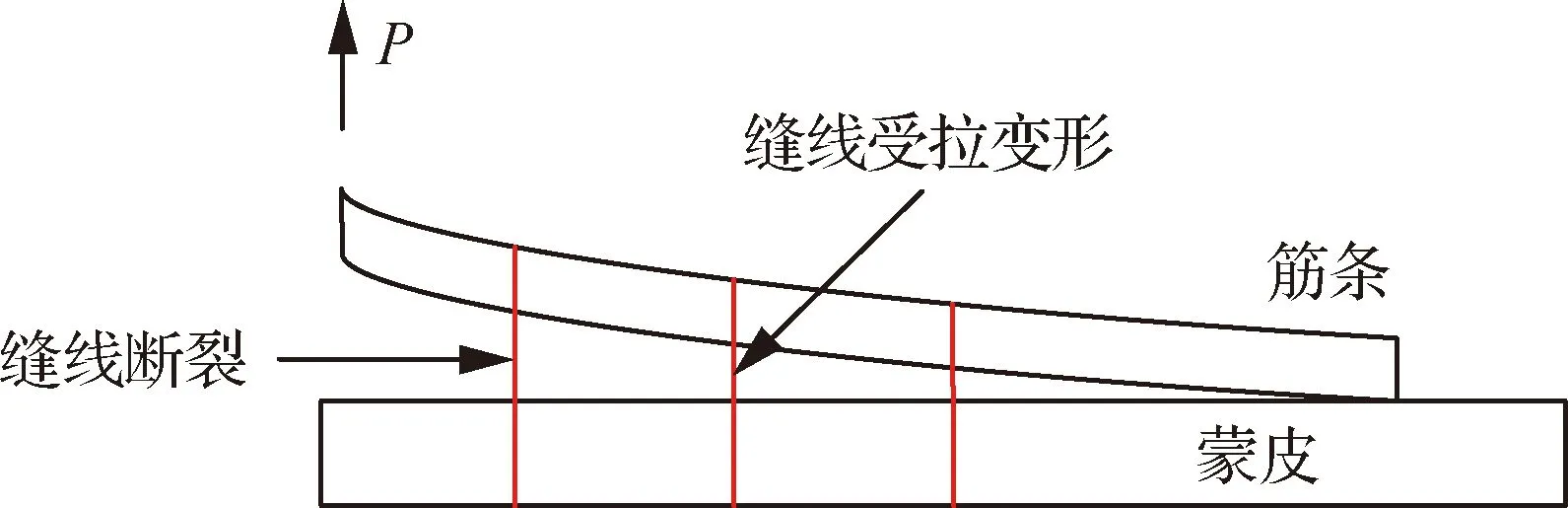
圖13 縫合T型接頭試樣界面脫粘示意圖Fig.13 Interface debonding of stitched T-joint sample

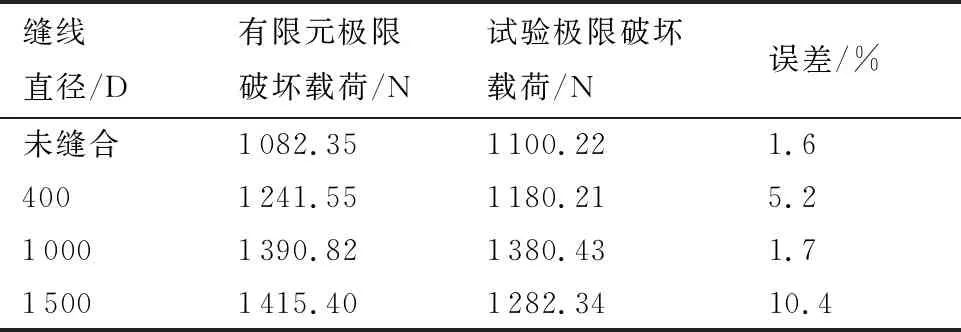
表6 T型接頭拉伸承載力模擬值與試驗值對比

4 結 論

本文建立了復合材料縫合T型接頭的有限元模型，研究了縫合T型接頭的界面失效機制及縫合參數對T型接頭拉脫承載能力的影響，得出以下結論：

1) T型接頭三維模型和二維模型有限元分析結果均和實際試驗吻合，驗證了分析方法的可行性、合理性。

2) 界面增強不會改變結構的初始破壞位置和最終破壞模式。

3) 縫合能夠有效提高T型接頭拉伸承載能力。

4) 隨縫線直徑增大，T型接頭極限破壞載荷提高，拉伸承載能力提高。由于模型未考慮縫合對層合板面內性能的影響，忽略了縫線可能造成的材料損傷，當縫線直徑增大到1 500 D時，與試驗結果存在10.4%的誤差。因此，在工程應用中不能一味增加縫線直徑和縫合密度，要在達到縫合結構性能目標的基礎上最大限度地降低縫合對層合板面內性能的不利影響。

[21] BIANCHI F, KOH T M, ZHANG X, et al. Finite element modelling of z-pinned composite T-joints[J]. Composites Science and Technology, 2012, 73: 48-56.