基于指數與倍數修正系數的天然氣產量預測方法優(yōu)化

陳艷茹余 果鄒源紅方一竹鄭 姝

（1.中國石油西南油氣田公司勘探開發(fā)研究院，610041；2.中國石油西南油氣田公司，610051）

0 引言

隨著國民經濟的增長及生產力的提高，油氣資源的需求量日益增加，油氣供需矛盾已成為影響我國經濟社會發(fā)展的重要因素。深入研究油氣儲產量變化規(guī)律并以此為依據建立預測模型，能夠科學預測我國未來油氣發(fā)展趨勢，對國家制定能源開采計劃及調整發(fā)展戰(zhàn)略具有重要意義［1］。油氣田產量大小受許多因素的影響，但從油氣開發(fā)全過程看，一般都要經過產量上升、產量相對穩(wěn)定、產量下降直至枯竭等幾個階段，具有典型的生命旋回特征，這是用峰值模型對油氣田開發(fā)全過程進行描述的客觀基礎。對具體的氣區(qū)或氣田（氣藏）產量趨勢進行預測時，選擇的峰值模型是否適宜，應以具體的實際分析為依據。由于各類峰值模型均有其適用條件與局限性，在峰值模型不能有效擬合具體氣區(qū)或氣田（氣藏）產量發(fā)展特點時，需要對其進行優(yōu)化與改進，并通過預測、檢驗，判斷其合理性，檢驗后的峰值模型才能適用于該區(qū)域的產量預測。

1 油氣產量預測模型

1.1 翁氏預測模型

對于油氣田資源開采體系，開采全周期過程可以用翁氏模型表述［2］：

式中，Q為油氣田產量，104t／a（油田）或108m3／a；t為翁氏時間，a；y為油氣田某一生產年份，單位a；y0為油氣田生產參考起始年份，a；n、A、C均為模型常數［3-4］。

將式（2）代入式（1）得到新的產量計算公式：

由于y-y0實際代表油氣田的實際生產時間，可采用油藏標準符號t代替，令t＝y(tǒng)-y0，B＝AC-n，a＝1C，那么式（3）可簡化為：

可采儲量為油氣開采全生命周期內的產量加和，推導NR公式如下

將式（4）代入式（5）可得：

令x＝at，式（6）可轉換為

式中，Γ(n)+1為完全伽馬函數，可通過查詢伽馬函數表獲得。

相應的剩余可采儲量公式如下

在計算可采儲量NR時，首先需要確定模型常數a、B，本文通過一種線性試差的方法進行求解。將式（4）兩邊取對數得到

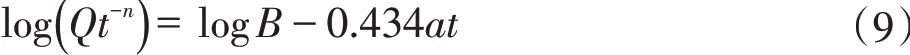
假設α＝logB，β＝-0.434 3a，可得線性試差方程如下：

通過采用不同的n值進行檢驗計算，選取使公式兩端線性相關性最好的n值作為計算指數，從而計算出模型常數a和B，再將模型常數代入產量與可采儲量式中計算，就可實現全生命周期產量預測。

1.2 Weibull預測模型

Weibull模型不但可以全周期預測油氣田產量，還可以預測油氣田的可采儲量、最高年產量及發(fā)生時間。其產量計算公式如下［5-7］：

為確定最高年產量的發(fā)生時間，由上式對時間t進行求導：

當dQ dt＝0，可得到最高產量的發(fā)生時間tm為：

為確定可采儲量NR和產量Q的數值，需確定模型參數α和β，將式（11）改寫為：

上式兩端取對數得：

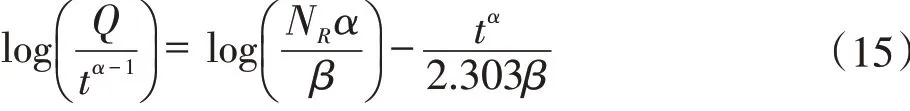
假如令

式（15）可以改寫為：

若給予不同的指數α值，開展試差法求取等號兩端線性相關性最高的α值［8-10］，利用該數值進行線性擬合，得到線性回歸方程的截距a和-b斜率的數值，并求出可采儲量NR及模型參數β。同理，將確定的模型參數代入產量式中，可實現全生命周期產量，最高年產量及發(fā)生時間的預測。

1.3 基于指數與倍數修正系數修正的產量預測模型

根據翁氏和Weibull兩種模型的產量計算公式（4）及式（11）可以看出，其預測結果受時間t的指數n和α的影響較大，指數的精準計算需要高精度地一次擬合Q與t的衍生式，指數的計算誤差容易造成產量預測結果出現指數倍的偏差［11-12］。因此，為糾正計算誤差，建立了一種指數及倍數修正因子方法，修正原理是分別在翁氏預測模型式（4）和Weibull預測模型式（11）中加入倍數修正系數和為指數修正系數，修正后的產量計算公式如式（19）及式（20）：

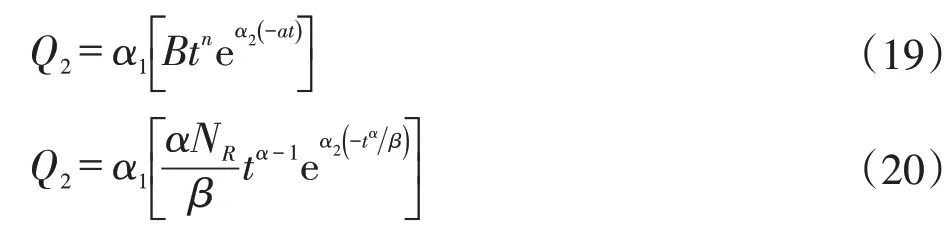
式中，Q2為修正后的產量值，單位104t／a（油田）或108m3／a；α1為倍數修正系數，無量綱；α2為指數修正系數，無量綱。

在產量Q的計算公式中，由于e指數函數的變化速度相對于t指數函數更快，因此在e指數中添加指數修正系數α2后，可以使預測曲線更接近原始曲線，同時通過α1修正整體倍數關系，可以進一步減小誤差。修正系數的計算原理如下：

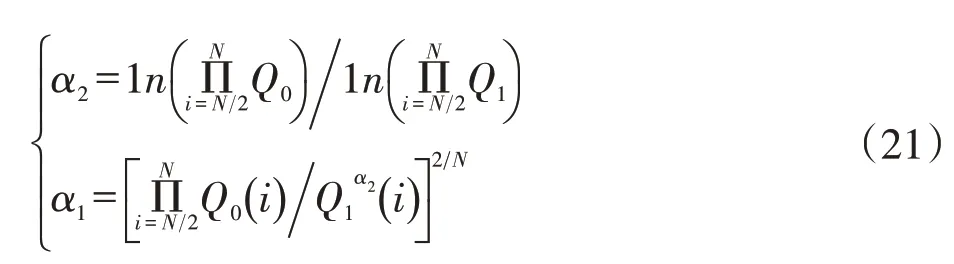
式中，Q0為原始產量值，單位104t／a（油田）或108m3／a；N為Q0序列包含的元素個數。

由于原始數值曲線隨著時間推移很難一直保持穩(wěn)定的函數關系，因此推薦選取原始數據的后半段作為參照修正值，對整體數值修正。

產量Q的t子函數的指數n與α影響產量的數值大小與曲線形狀，指數與倍數系數僅能減小Q的數值計算誤差，不能修正Q的變化規(guī)律。因此，在修正計算后，在原指數n與α附近重新選取多個指數的數值再次計算，與原始數值Q0進行相關性分析，選取使公式兩端線性相關性最好的指數值作為計算指數。基于指數與倍數修正系數進行改進的預測模型可以減少修正預測模型與原始數據變化規(guī)律的誤差，提高擬合精度，使預測結果更加可靠。

2 應用舉例

四川盆地為典型的大型復雜疊合盆地，歷經60余年的勘探開發(fā)，主要經歷三個階段：1953-1977年的探索起步階段，1978-2004年的穩(wěn)步增長，2005年至今的發(fā)展壯大階段。伴隨勘探開發(fā)節(jié)奏，盆地的天然氣產量發(fā)展也出現了三個明顯的峰谷起伏，整體上仍呈現持續(xù)增長的態(tài)勢，如圖1所示。考慮年產氣量整體呈上升趨勢，伴隨較小的局部峰，局部波動處的數值突變較小，對整體類指數增長趨勢影響較小，因此產量計算可采用翁氏和Weibull單峰值預測模型方法。

以四川盆地1953-2019年的天然氣歷史產量數據為基礎，通過歷史數據擬合，檢驗相關性合格后再預測分析至2140年產量變化趨勢。將1953年作為原始時間點t＝0，t＝1時間點代表1954年，其他時間點依次類推。首先，采用傳統(tǒng)翁氏預測方法的產量衍生式與時間進行擬合，由于產量Q的衍生式與時間t不完全呈線性關系，因此分別選取t＝30～50及t＝55～60兩段線性特點較好的數值點進行階段線性擬合（圖2）。如圖3所示，為產量的擬合結果與原始數值對比，可以看出兩種擬合結果僅在相應時間段內精確度較高，整體上偏離了四川盆地實際的產量發(fā)展趨勢，因此傳統(tǒng)模型是不適用于四川盆地天然氣產量預測的。

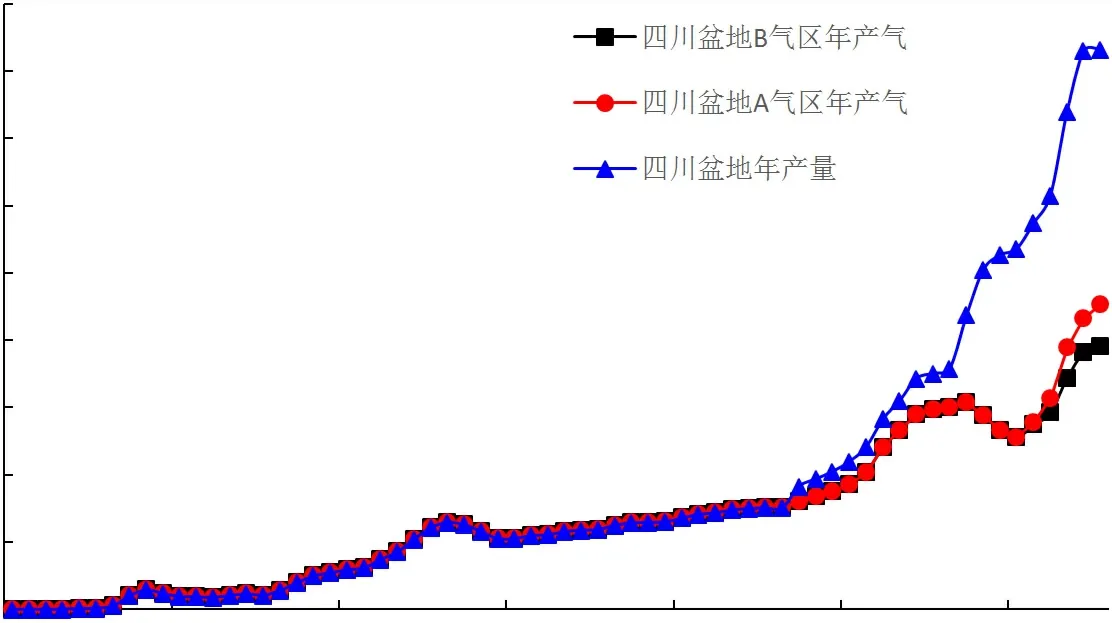
圖1 四川盆地年產量原始數據圖

圖2 產量衍生公式與時間的線性擬合

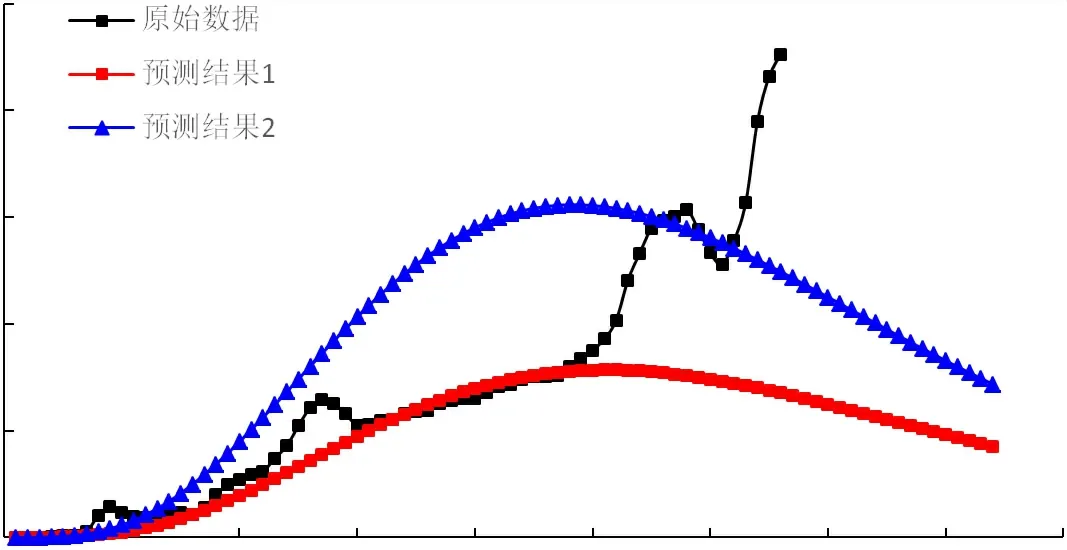
圖3 產量線性擬合預測結果

采用指數與倍數修正系數改進的翁氏與Weibull模型，在整體線性擬合的基礎上再進行系數修正校正擬合結果，改進后模型的預測曲線與四川盆地天然氣歷史產量曲線較為接近，擬合相關性高，可適用于四川盆地天然氣產量預測。通過指數及倍數擬合修正后，再選取原始翁氏模型指數N及Weibull模型指數附近的值代入計算，可得到不同指數條件下的產量預測曲線，如圖4～圖9所示。

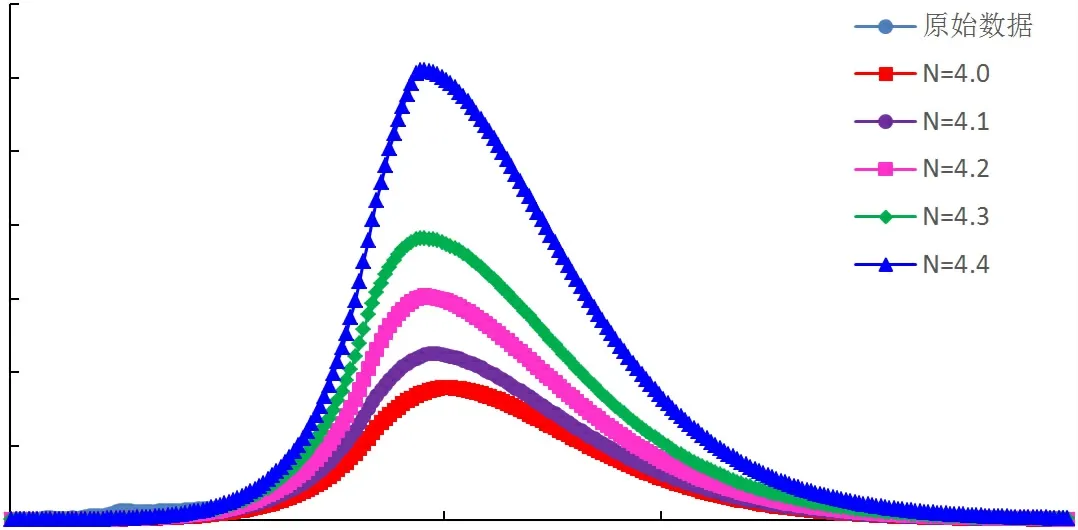
圖4 翁氏模型四川盆地A氣區(qū)年氣產量預測結果

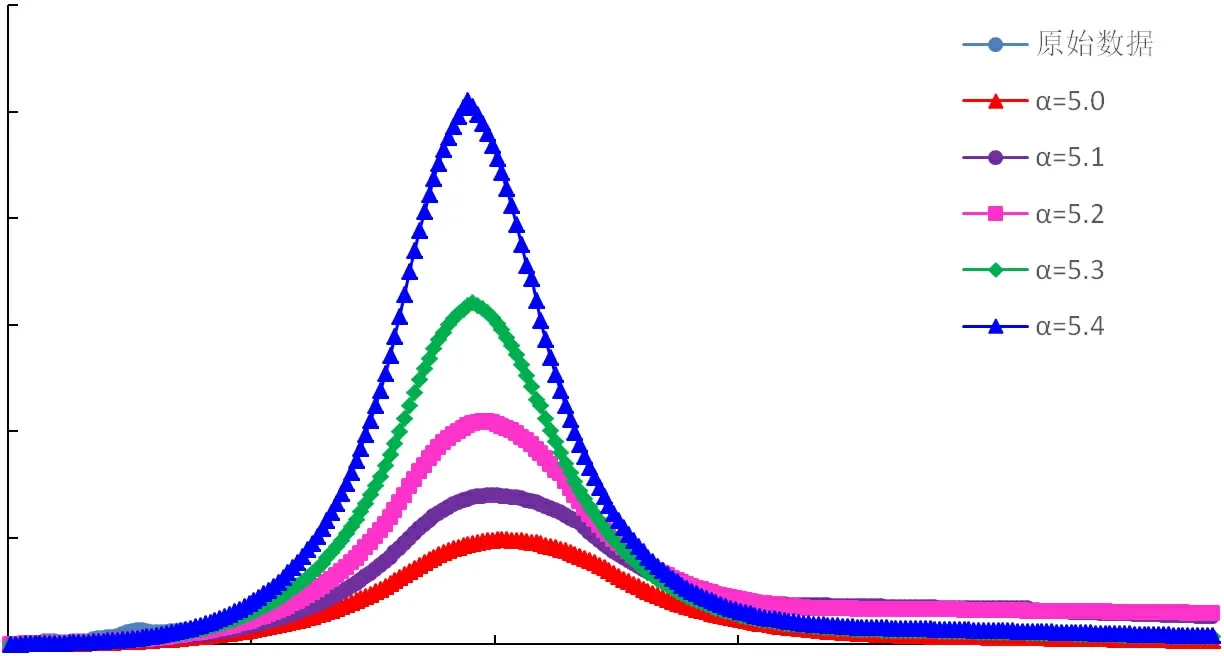
圖5 Weibull模型四川盆地A氣區(qū)年氣產量預測圖

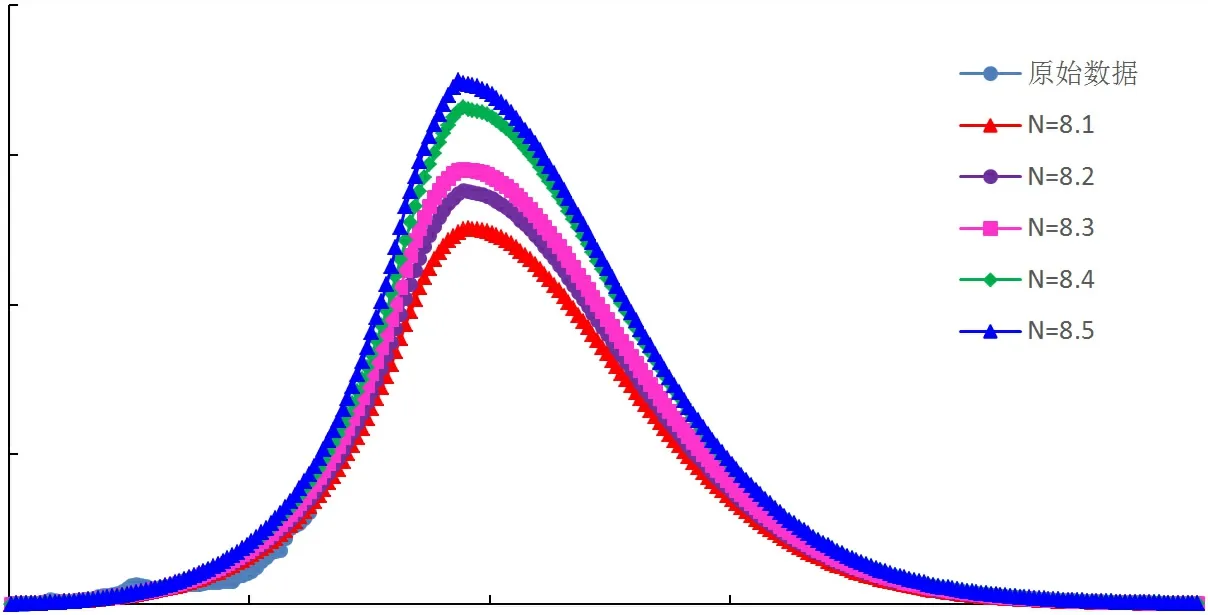
圖6 翁氏模型四川盆地年氣產量預測結果

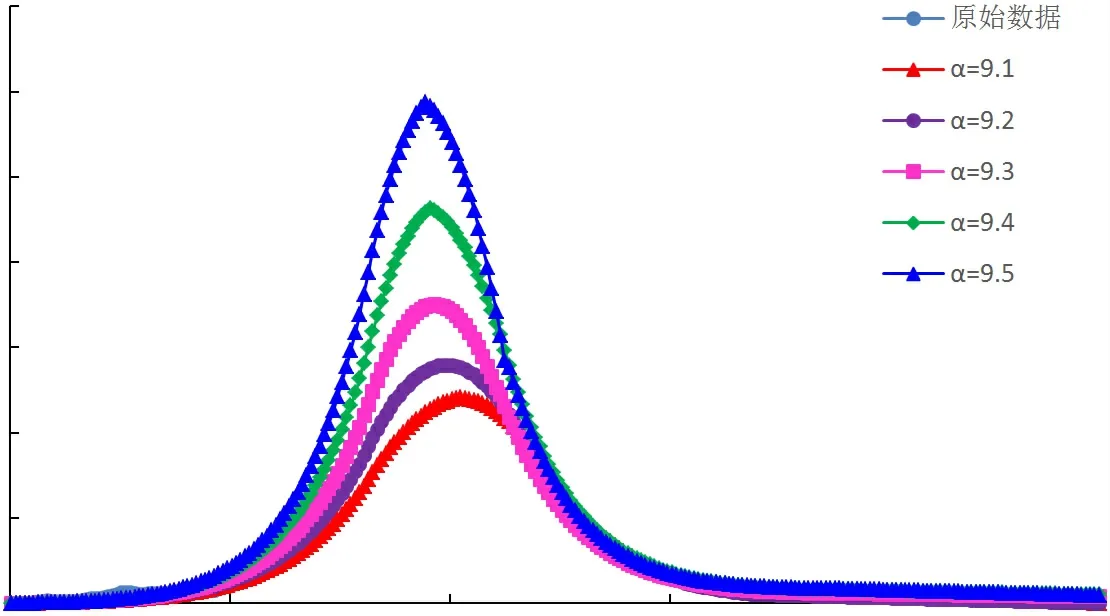
圖7 Weibull模型四川盆地年氣產量預測結果

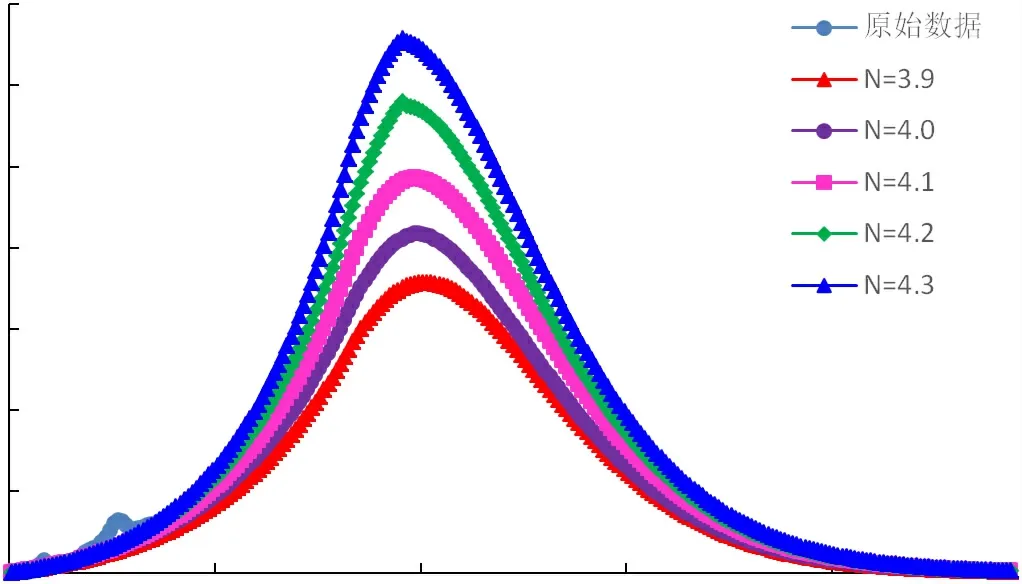
圖8 翁氏模型四川盆地B氣區(qū)年氣產量預測結果

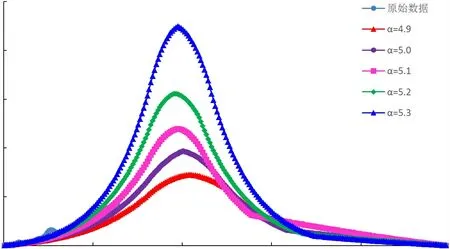
圖9 Weibull模型四川盆地B氣區(qū)年氣產量預測結果

將不同產量預測曲線的計算結果與原始數據進行相關性分析，選取相關性最好的一組作為預測模型，最終預測模型的相關系數、最大產量及其發(fā)生時間如表1所示。總的來說，兩種修正后模型的預測結果相接近：①改進翁氏模型預測四川盆地峰值產量時間出現在2047年，峰值產量為1 453.28×108m3；改進Weibull模型預測四川盆地峰值產量時間出現在2049年，峰值產量為1 750.38×108m3。②改進翁氏模型預測四川盆地A氣區(qū)峰值產量時間出現在2050年，峰值產量為1 128.81×108m3；改進Weibull模型預測四川盆地A氣區(qū)峰值產量時間出現在2050年，峰值產量為1 047.88×108m3。③改進翁氏模型預測四川盆地B氣區(qū)峰值產量時間出現在2051年，峰值產量為486.46×108m3；改進Weibull模型預測四川盆地B氣區(qū)峰值產量時間出現在2050年，峰值產量為478.40×108m3。

應用表明，基于指數與倍數修正系數修正的翁氏及Weibull預測模型能充分擬合四川盆地產量的整體發(fā)展趨勢及歷次產量突變，預測結果顯示出四川盆地發(fā)展?jié)摿薮螅磥?0年左右將是其產量的快速發(fā)展期，對整體氣區(qū)或氣田（氣藏）中長期發(fā)展戰(zhàn)略的制定具有較好的指導作用。但天然氣產量預測是一個復雜的過程，僅以數學原理為基礎的預測模型不能完全考慮地質條件、開發(fā)技術政策等各環(huán)節(jié)的影響，實際應用中還需要結合氣區(qū)或氣田（氣藏）的階段發(fā)展形勢進行綜合考慮。

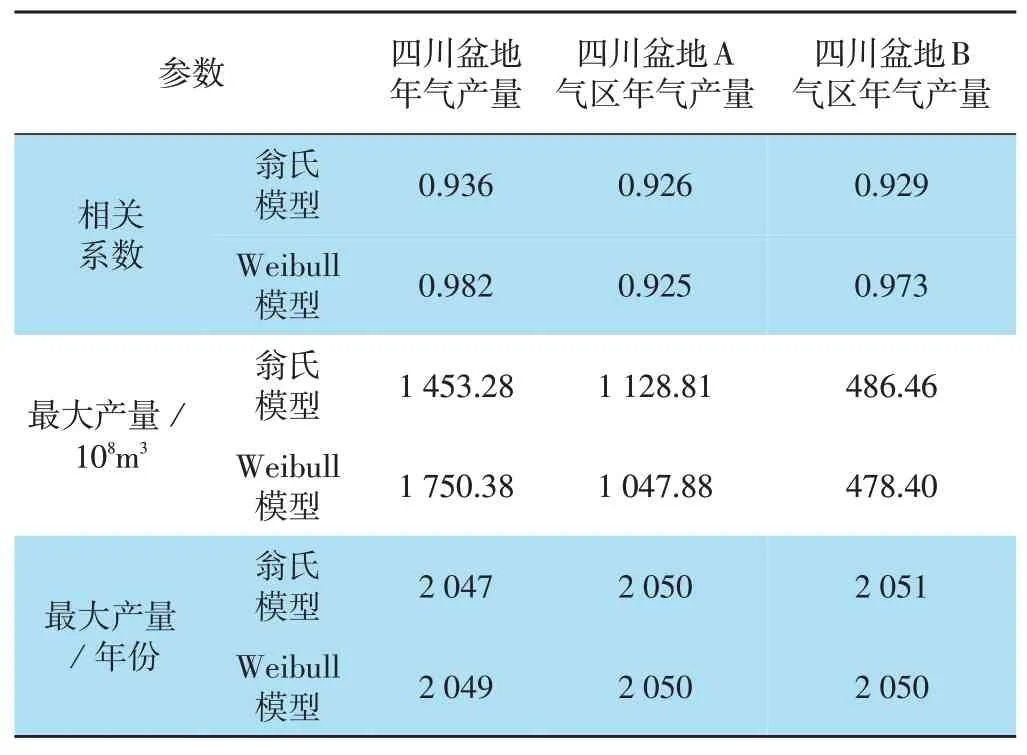
表1 四川盆地年產量數據統(tǒng)計

3 結論

1）傳統(tǒng)的翁氏和Weibull產量預測模型受線性擬合計算影響較大，易造成指數倍的誤差。使用雙權重修正因子方法可以修正計算誤差，基于原始數據建立的倍數修正系數α1和α2指數修正系數可以精準地校正計算結果。

2）在修正系數計算的基礎上，利用t子函數指數多值求解產量，并與原始數據相關分析選取更優(yōu)解。t指數修正法可以減少預測曲線與原始數據變化規(guī)律的差異性。

3）通過四川盆地預測模型的構建，發(fā)現基于上述方法改進的翁氏模型和Weibull模型均能夠較準確盆地全生命周期的產量變化趨勢，且兩種算法得出的預測值接近，都具有較高的精準度。