基于變分模態分解和粒子群算法的微震信號降噪方法①

鄧紅衛， 申一鵬

(中南大學 資源與安全工程學院,湖南 長沙410083)

微震監測是一種三維空間監測技術,可以監測到礦山開采作業中發生的巖體破裂現象,對了解巖體內部破裂及損傷演化過程和指導礦山安全生產有著重要作用。 但是采集到的微震信號往往受電磁噪聲、機械振動等背景干擾,另外爆破振動信號往往混雜于巖體破裂信號中,難以識別,因此,如何有效識別微震信號是一大難題。

微震信號具有非平穩性、隨機性的特點,傳統傅立葉變換［1］不能反映信號的細節問題,對于非平穩信號的時頻描述和降噪效果不佳。 常見的處理非平穩信號的方法包括經驗模態分解、小波變換、ST 變換等［1-11］。

變分模態分解(Variational Mode Decomposition,VMD)［12］是一種新的非遞歸式信號處理方法,不同于傳統經驗模態分解算法遞歸式獲得分量的過程,變分模態分解通過構造約束變分模型,將模態估計轉化為變分問題,信號被分解為一系列圍繞在中心頻率周圍的模態分量,各個模態分量之間具有良好的稀疏性。與集合經驗模態分解(EEMD)相比,VMD 具有堅實的理論基礎,克服其模態混疊和計算量大的缺點,噪聲魯棒性好,具有良好的去噪效果［13］。 在用VMD 算法對微震信號的研究過程中,均通過主頻觀察法來確定分解模態數［14-15］,當中心頻率相近時認為出現過分解現象,此模態數選取方法較為復雜,缺乏自適應性,且忽略了懲罰因子對分解結果的影響。 本文在深入研究各去噪方法的優缺點后,提出一種改進的VMD 方法對微震信號進行降噪,并以降噪信號第一模態分量的能量占比作為特征閾值,實現爆破振動信號和巖體破裂信號的識別。

1 變分模態分解的基本原理

變分模態分解(VMD)將本征模態函數IMF 定義為一個調頻-調幅信號,表達式為:

式中Ak(t)為uk(t)的瞬時幅值；相位wk(t)＝φk′(t),是uk(t)的瞬時頻率；k 是固有模態的數,而uk(t)被認為是一個幅值為Ak(t)、頻率為wk(t)的諧波信號。 此時原信號被分解為k 個有限帶寬的IMF 分量uk(t),各個IMF 的中心頻率為wk(t)。

為使每個模態函數的估計帶寬之和最小,構造如下的約束變分模型:

為了求解上述約束變分模型,引入二次懲罰因子α 和拉格朗日乘子λ(t)將其變為不受約束的尋優問題,其中α 用來保持信號的重構精度,λ(t)則用來保持約束條件的嚴格性,其增廣拉格朗日方程為:

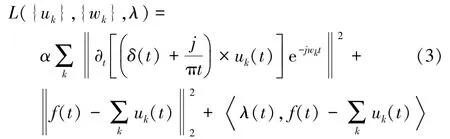
采用乘法算子交替方向法來解決變分問題,通過不斷更新各IMF 及其中心頻率得到上述函數的最優解。 所有頻域中的IMF 可通過式(4)獲得:

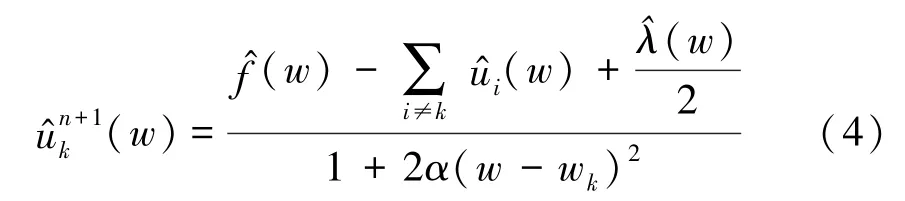
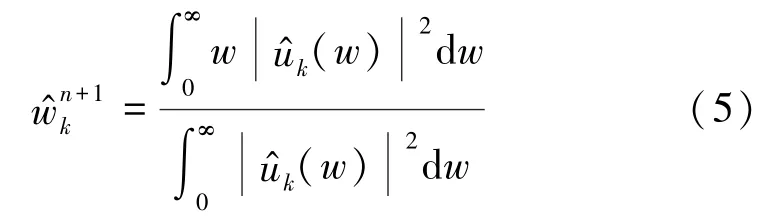
VMD 算法的迭代過程如下:

2) 根據式(4)、(5)在頻域內更新uk、wk；

3) 更新λ,其中:

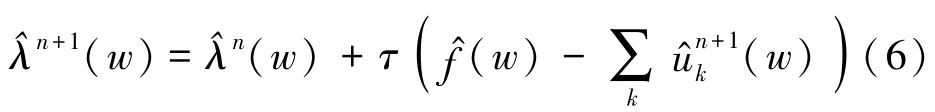
2 改進的變分模態分解

VMD 算法中的兩個主要參數k 和α 對分解結果有顯著影響。 k 過小會使模態分量信息丟失,造成頻率混疊現象；k 過大則會造成過分解現象。 α 與分解模態的帶寬有關,通過增大α 來減小帶寬可能會抓取錯的中心頻率；太小的α 又會使估計模態包含很多噪聲。 同時,α 對帶寬的作用會進一步影響到各模態所獲能量的大小,進而影響k。

本文提出的改進VMD 算法利用粒子群算法來優化k 和α 值的選取,并通過小波閾值去噪法對初步分解的信號高頻分量進一步降噪。

2.1 粒子群算法原理

粒子群算法(PSO)是模擬鳥群覓食的一種進化算法,相比其他的進化算法如蟻群算法和遺傳算法等具有收斂性更快和計算量更小的優勢。 在粒子群算法中,構造了D 維粒子和適應度函數。 PSO 的目的是通過遞歸更新所有粒子的位置和速度,直到滿足終止條件,從而獲得最佳的適應度函數。

本文定義VRMSE和VCC的比值作為粒子群算法的適應度函數,其中VRMSE是原始信號和重構信號的均方誤差根,VCC是它們之間的互相關系數。 適應度函數為:

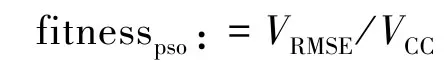
當k 和α 取值達到最優時,重構信號和原始信號之間的均方誤差根應該最小,互相關系數達到最大,此時適應度函數達到最小值,粒子群算法取得最優解,停止迭代。

2.2 小波閾值去噪

小波閾值去噪［16-17］是在小波變換基礎上發展出來的一種新的去噪算法,適合對分解信號進行多尺度的細化。 本文通過VMD 聯合小波閾值去噪,綜合兩種方法優點,對含噪較多的高頻分量進行去噪處理。小波閾值去噪的具體步驟可歸納如下:

1) 信號的小波分解。 根據小波基函數和待測信號的特點,選擇合適的小波基函數并確定分解層數N,用該小波基函數對噪聲信號進行N 層小波分解,得到經小波變換后的小波系數ωj,i。 其中包括目標信號對應的小波系數uj,i和噪聲信號對應的小波系數vj,i。

2) 小波分解后的閾值量化。 根據小波分解后系數的不同幅值大小,選擇一個合適的閾值,進行量化處理。

3) 小波重構。 根據小波分解第N 層的低頻系數和經過量化處理后的第1 層到第N 層的高頻系數,進行信號的逆小波變化。

2.3 OVMD 算法

改進的VMD 算法(OVMD)步驟如下:

1) 初始化PSO 各項參數,構造適應度函數,其中的懲罰因子α 和分解個數k 的尋優范圍分別設置為［2,10］和［100,5 000］。

2) 對比各粒子適應度函數大小,更新粒子位置。

3) 判斷粒子是否滿足種群進化停止條件,若不滿足則重復步驟2)繼續尋優,直到滿足最大種群進化預設值。

4) 以獲取的最優參數對指定微震信號進行分解,得到N 個本征模態分量imfi。

5) 對高頻噪聲主導的模態分量imfk～imfn進行小波閾值去噪,得到imfk′～imfn′。

3 實例分析

從某金礦微震監測系統采集到的巖體破裂信號中,抽取200 組信號利用OVMD 算法進行降噪,采樣頻率為2 000 Hz,經粒子群算法優化后k ＝6,α＝3 500。降噪前后信號波形其頻譜如圖1 所示。

對比降噪前后巖體破裂信號的波形及頻譜圖可以看出,降噪后信號較降噪前清晰,尤其是50 Hz 的工頻噪聲被明顯剔除,而高頻噪聲部分也得到很大程度地壓制,整體降噪效果明顯。 由此可見,改進的變分模態分解法對于微震信號有較好的降噪效果,工頻噪聲和高頻隨機噪聲濾波效果明顯。

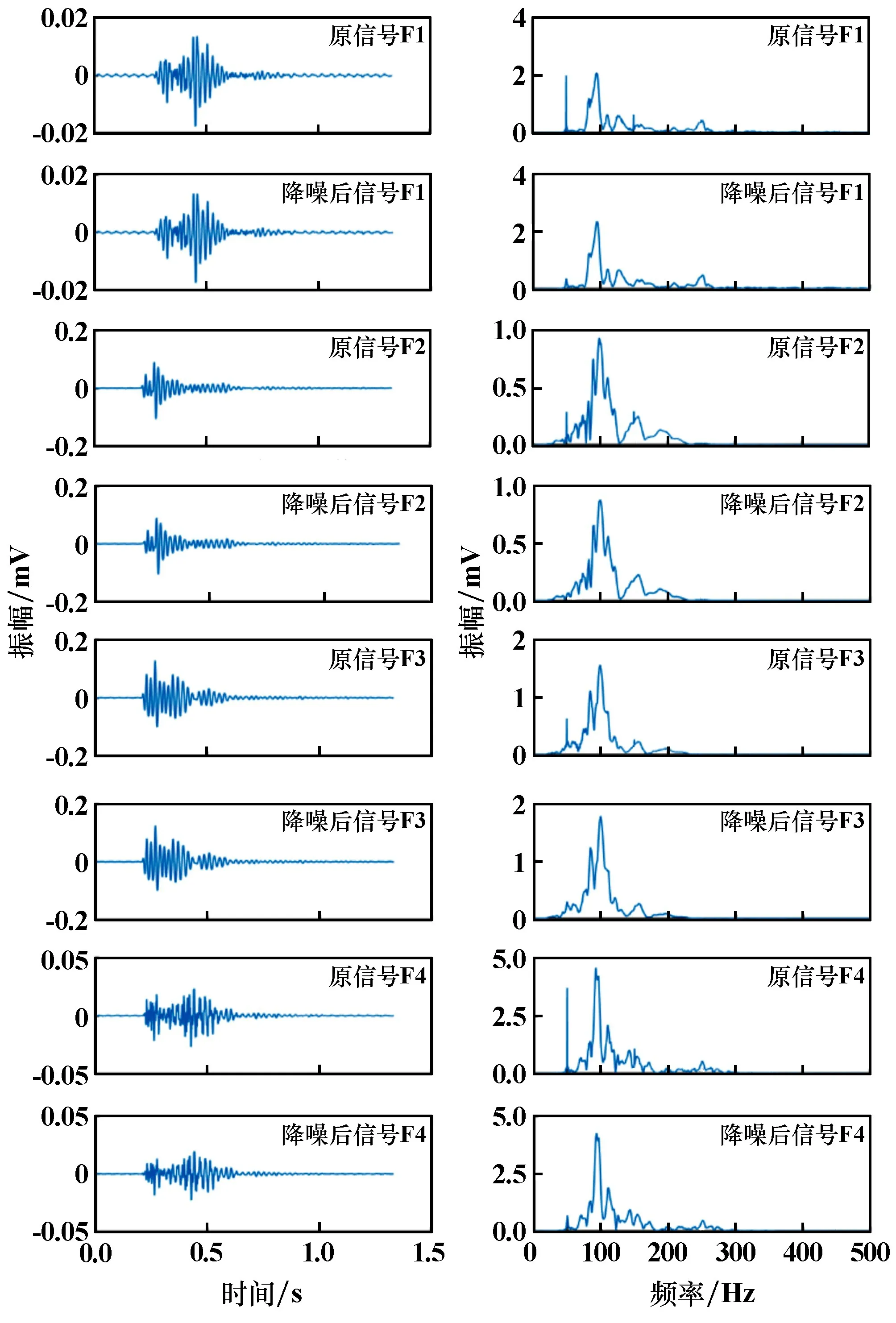
圖1 含噪巖體破裂信號的分解結果及頻譜

為驗證改進VMD 算法的去噪效果,將本文方法與VMD 及EEMD 對含噪微震信號的降噪結果進行對比,分別通過信號降噪前后的信噪比SNR、原信號與降噪后信號的均方誤差根RMSE 和降噪后信號占原信號的能量百分比ESN 來評價對巖體破裂信號的降噪效果。 計算結果如表1 所示。

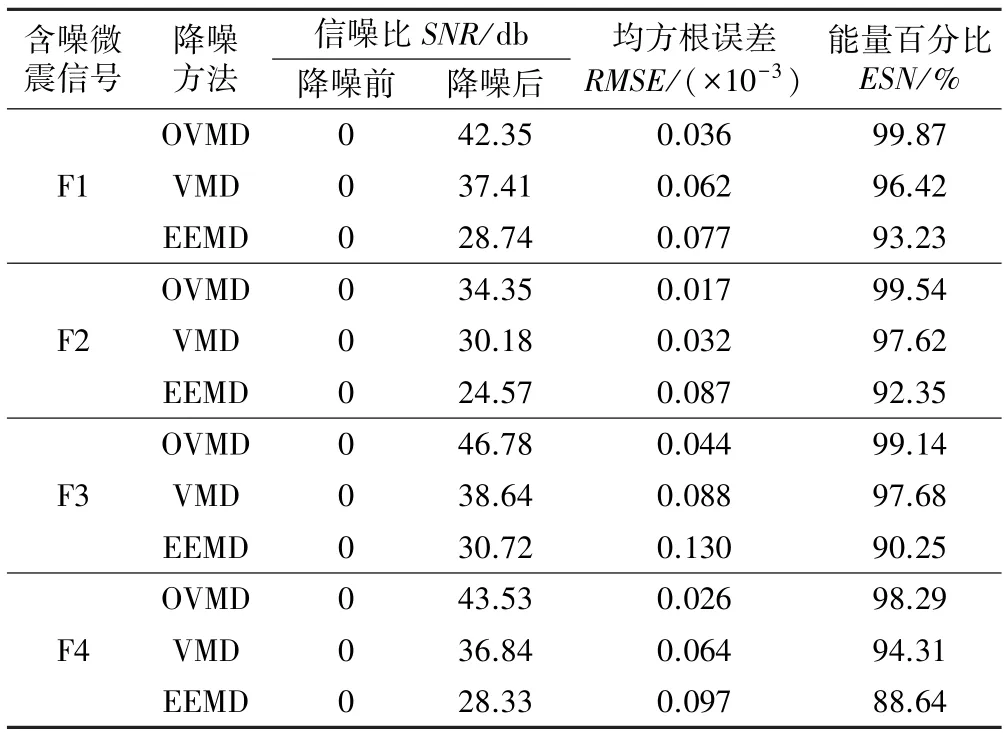
表1 降噪效果對比分析

分析表1 可得,3 種方法都可對微震信號進行一定程度的降噪,其中,傳統EMD 算法對信號的降噪效果最差,信噪比較低,改進的VMD 算法去噪效果最好。 從降噪前后信號的均方誤差跟和能量百分比來看,改進的VMD 算法對有效信號保留最多,降噪后的信號在形態上更接近原信號；VMD 和EMD 算法則對原信號中的有效信號部分有較大程度的剔除。

4 信號識別

礦井的微震監測系統除了監測井下巖體破裂活動,還能監測到爆破振動,但兩者僅從外形上難以區分,人工區分兩種信號難度較大。 通過對數據庫大量的兩種信號進行分析發現,巖體破裂信號的頻率在0～200 Hz 范圍內,優勢頻率主要在50～150 Hz；而爆破振動信號的頻率范圍較廣,分布在100 ～500 Hz 范圍內,優勢頻率主要集中在200 ～350 Hz 范圍內。 圖2 為兩種信號的波形及頻譜圖。

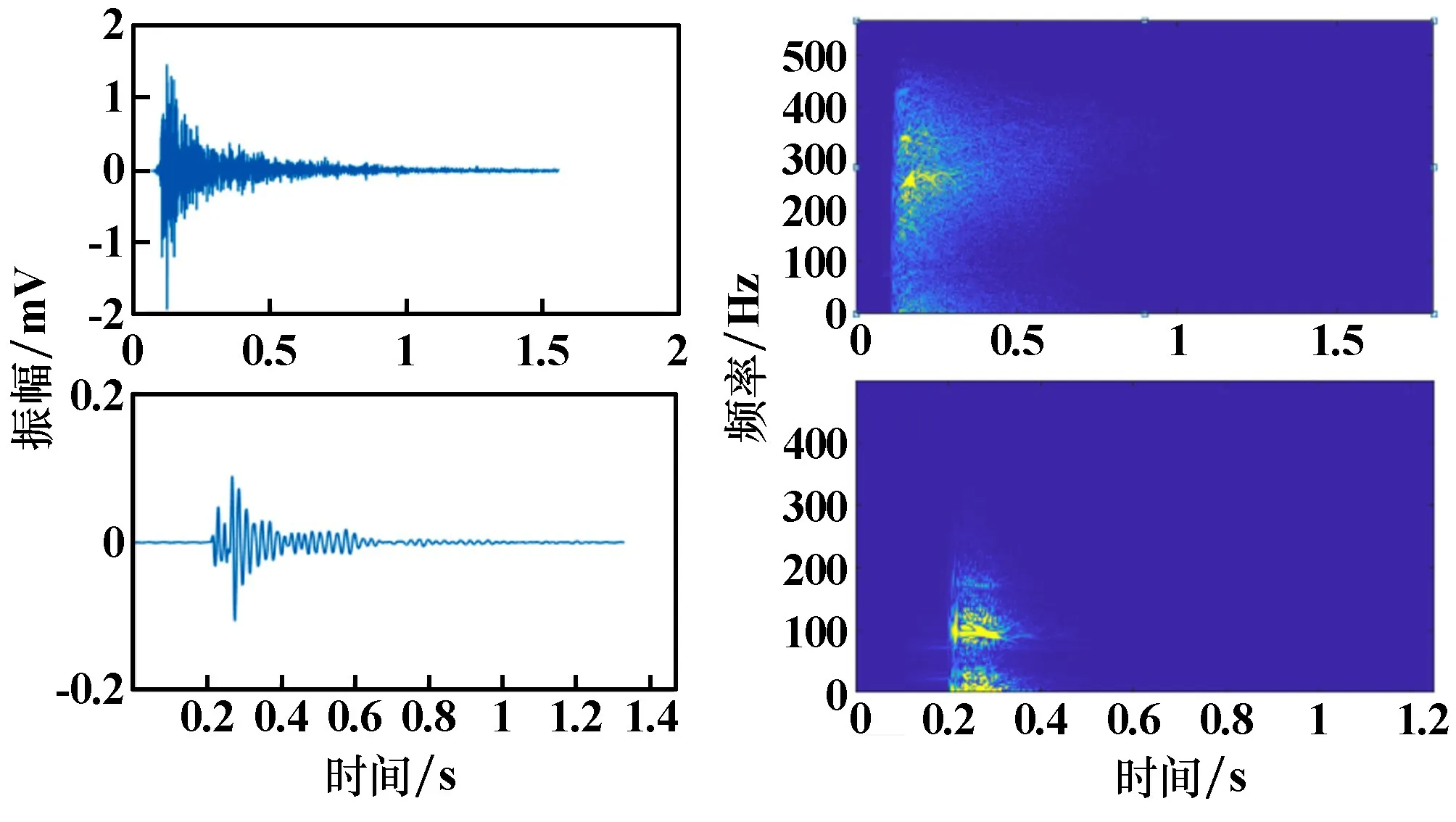
圖2 含噪巖體破裂信號的分解結果及頻譜

隨機抽取4 組巖體破裂信號(F1～F4)和4 組爆破振動信號(R1～R4),分別對兩種微震信號進行OVMD降噪,統計4 組巖體破裂信號和爆破振動信號每個模態分量的能量比值,結果見表2。

表2 微震信號在各模態的能量比值

從表2 可以看出,經改進VMD 算法降噪后的巖體破裂信號中,模態1 的能量占比很高,達到60%以上,而爆破振動信號經VMD 分解后的模態1 中,能量占比低于10%。 這是由于模態1 是VMD 分解的低頻分量,無論是巖體破裂信號還是爆破振動信號,模態1 的頻率范圍均小于150 Hz。

將模態1 信號分量的能量占比作為識別巖體破裂信號和爆破振動信號的特征閾值,能量占比高于50%認為是巖體破裂信號,否則為爆破振動信號。 為驗證此分類判據的可靠性,對全部400 組信號進行分類識別,結果如表3 所示。

表3 微震信號識別效果

從表3 可以看出,經由VMD 聯合小波閾值去噪后,對巖體破裂信號的識別準確率達到98.0%,對爆破振動信號的識別準確率達到96.5%,綜合識別成功率達到97.25%。

5 結 論

1) 本文提出的改進VMD 方法,通過粒子群算法來優化模態數量和懲罰因子取值,并通過小波閾值去噪法對含噪高頻分量進一步去噪,能有效去除微震信號的隨機噪聲,最大程度地保留原始信號的形態特征,降噪后的信號與原信號有很好的相似性。

2) 實驗結果表明,OVMD 方法降噪效果優于EEMD 方法和VMD 方法,具有較高的信噪比和較低的均方根誤差。

3) 以OVMD 分解得到的第一個模態分量的能量占比50%作為特征閾值來識別巖體破裂信號和爆破振動信號,辨識效果準確,證實了本文改進變分模態分解方法的有效性。