不確定時滯神經網絡魯棒采樣同步控制研究
張贛雷,王春柱,謝立典,王嘉偉,葛超
(1.華北理工大學人工智能學院,唐山063200;2.火箭軍綜合訓練基地學兵訓練一隊,唐山064000;3.石家莊海山實業發展總公司,石家莊050200)
0 引言
在研究神經網絡這一典型非線性系統中,人們發現時延是一個不容忽視的問題,它會影響系統的動力學行為。已有的研究大致可以劃分為兩類,帶時延和不帶時延。顯然,帶時延的研究具有更低的保守性[1-3]。本文引入了兩種時延,離散時延和分布式時延。
不確定性和干擾廣泛存在于神經網絡系統中,它們會影響系統的性能甚至造成系統的不穩定。因此,研究帶有不確定性和干擾的神經網絡具有重要的現實意義[4-5]。文獻[4]提出了一種不確定神經網絡的變結構控制方法,有效地控制住了系統中的“抖振”問題。文獻[5]借助H∞最優控制方法和滑模控制理論,提出了一種針對具有執行器故障和干擾的不確定神經網絡的控制方案。
本文研究了帶有干擾和不確定性的時滯神經網絡的魯棒同步問題。通過構建帶有時滯信息的LKF,利用新的積分不等式、舒爾補定理和凸組合技術,推導出了具有更低保守性的結果。最后利用一個仿真實驗驗證了所提方法的有效性。
1 問題闡述
考慮如下不確定時滯神經網絡系統:


其中,tk≤t 下面給出的定理和引理將被應用于證明過程中。 定義1 給定兩個正數a和b,若以下不等式成立,則系統(1)和(4)實現了指數同步,系統(6)實現了指數穩定。 對于滿足FT(t)F(t)≤I條件的函數F(t) 和標量σ>0 而言,以下不等式成立: W1+σHHT+σ-1ETE<0 本部分內容將給出SES 的穩定判據,推導增益矩陣K。為了簡化矩陣表述,特給出以下表述符號: 顯然,主從系統實現了穩定,增益矩陣K可以通過K=G-1L求得。 本部分將對推論1 進行實驗驗證。 考慮具有如下參數矩陣的神經網絡系統: 表1 列舉了不同h 下的最大同步率α。可以看出,相較于文獻[1]和[3],在相同情況下,本文提出的方法能夠更快實現SES 的同步,從而例證本文列舉方法的有效性。 表1 不同h 下的最大同步率α 通過求解LMIs(28)-(31),對應的控制器增益矩陣K為: 通過求得的增益矩陣K,我們可以畫出誤差e(t)(圖1)和控制器u(t)(圖2)軌跡曲線。圖3 顯示出誤差隨著時間增長趨近于零,即驗證了我們方法的有效性。 圖1 誤差e(t) 圖2 控制器u(t) 本文基于李雅普諾夫穩定性理論,通過構造新型泛函,利用新的積分不等式和凸組合技術,研究了帶有干擾和不確定性的時滯神經網絡的魯棒同步問題。實驗結果驗證了本方法的有效性。

2 主要成果




3 仿真實驗


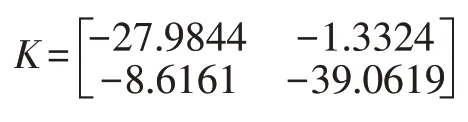


4 結語

