短除法教學爭鳴

泮玲玲

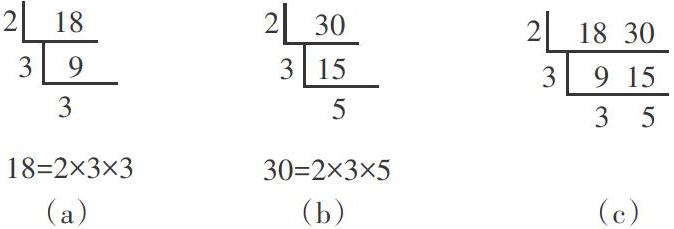
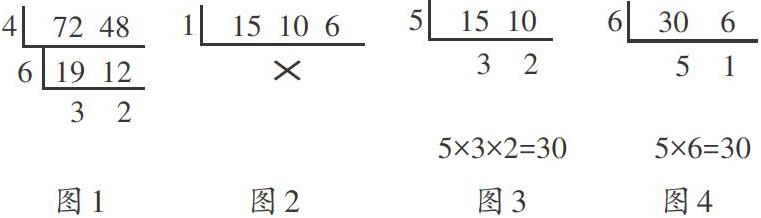
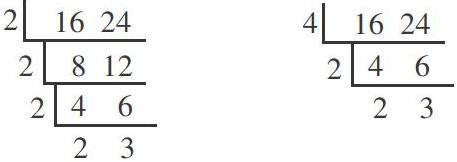
[摘 要]短除法作為計算兩個數最大公因數和最小公倍數的一種偏方，不失為一個簡明實用的方法，但是，其中涉及的算理頗為復雜，計算兩個數的最大公因數和最小公倍數時，又有交叉的部分，不如列舉法來得直觀明了，因此在教學處理時需要慎重對待。

[關鍵詞]短除法;算理;公因數;公倍數;最大;最小

[中圖分類號] G623.5[文獻標識碼] A[文章編號] 1007-9068（2021）08-0028-02

有幸拜讀劉暢老師的論文《重在怎樣教“短除法”》（下文統稱為“《劉版》”）和陸曉林老師的論文《也談“短除法”》（下文統稱為“《陸版》”），讀罷兩文，筆者不禁掩卷而思。對于短除法，在現行課標部署下，教材一般作出兩種處理方案：一種方案是將短除法這一知識點作為計算最大公因數和最小公倍數（后文簡稱“兩最”）的拓展內容，作為番外篇單獨編排在附錄中，是否教學該內容讓一線教師難以取舍。另一種方案是將短除法作為正式內容放入主篇幅，簡省了算理分析只教算法，這樣一來，雖然是必修內容，但是講不講解算理也讓教師頗為躊躇。

《劉版》的看法是教短除法責無旁貸，并從算理的角度作了詳細論述;而《陸版》則以實驗班和普通班作為對象進行對照試驗，傾向于放棄短除法的教學，認為“棄用短除法啟用列舉法才是兩利相權取其重”。下面結合兩位前輩的觀點與筆者個人的教學實踐淺談個人思考。

一、短除法的算理剖析

運用短除法求算“兩最”的理論基礎是分解質因數，對兩個數分別分解質因數，然后提取共有質因數（相同質因數要重復計算），這樣一來就會羅列出兩個數的全體共有質因數以及各自的獨有質因數，最終將各個共有質因數相乘求出最大公因數（全體共有質因數相乘的積），全體共有質因數與各自獨有質因數相乘求出最小公倍數。分解質因數的通用方法是短除法，如下圖中（a）和（b）所示;在求“兩最”的實際演算操作中，往往將分解質因數和篩選共有質因數合二為一，同步推進，將兩個數放入一個短除號內進行同步分解，如下圖中（c）所示，因此求幾個數的“兩最”的短除算式應運而生。

分解質因數的理論基礎是算術公理，其內容是：任意一個大于1的自然數，都能分解成若干個質數的積，并且如果不計較排序，這樣的分解式是獨一無二的。顯然，將一個數分解質因數后，得到的質因數乘式是唯一的，即任何一個數的質因數的大小與數量是固定的，因此，兩個數的共有質因數的大小以及數量也是固定的，剩下的獨有因數也是不變的;另一方面，由于每個數都是通過一步步做除法求出質因數，各個質因數之間是相乘的關系，這也證實了利用“乘積”求出“兩最”的合理性。求“兩最”的短除法與分解單個數的質因數如出一轍，唯一加以改造的是，利用“兩個數的所有共有質因數是它們最大公因數的因數，兩個數的最小公倍數是它們所有共有質因數和獨有因數的乘積”這一定律。

現以計算18和30的“兩最”為例來闡述。把18和30分別分解質因數：

（1）求它們的最大公因數的原理剖析：

18=2×3×3

30=2×3×5

由分解質因數的結果可以直接判斷，18和30的共有質因數為一個2和一個3，于是全體共有質因數的乘積為2×3=6。毫無疑問，這個乘積是18和30的公因數，且這個乘積是將所有共有質因數求積得出的，它必然是公因數中最大的那個。如此，兩數的最大公因數必然是兩數所有共有質因數的乘積。

（2）計算兩數最小公倍數的原理剖析：18和30的所有公倍數，一定都是18的倍數，根據倍數的傳遞性，勢必同時是18的所有因數（包括非質因數）的倍數，同理，18和30的所有公倍數也一定是30的倍數，同時也是30的所有因數（包括非質因數）的倍數，等于是兩個數所有因數的乘積的倍數。而我們要求的是最小公倍數，所以，其中包含的質因數應該盡可能少，唯一的可能是在所有的共有質因數上做文章，對每個共有質因數只算一次，不重復計算，于是18和30的最小公倍數=2×3×3×5=90。這個乘式中，2和第一個3是兩數的共有質因數，第二個3和5分別是兩數的獨有質因數，為了確保結果是兩個數的公倍數，要一一計算。不言而喻，兩個數的最小公倍數，其實就是兩數所有共有質因數與獨有質因數的總乘積。

二、“短除法”的教學反思

1.短除法是小學生的必備技能。短除法的格式簡潔直觀，充分體現了求“兩最”的流程、算理、技巧，算式美觀整齊，易學易懂易操作。實踐證明，學生在求“兩最”時，樂于使用短除法。比如：在“求最大公因數”的綜合應用題中，計算、約分等步驟，一般都是處理兩個數，按照短除法的原理，先預判兩數是否為2、3、5的倍數，然后直接用兩個數的共有質因數進行整除，一步步化為最簡分數。再如解答“最小公倍數”應用題時，在計算、分母通分時，用短除法更容易找出兩個分數的最小公分母，步驟簡練，計算的效率和準確性也有了保障。

2.不教算理，只學算法。從教材承擔的功能來說，無論是正式篇章還是插敘的內容，通常都安排在列舉法之后，以“小竅門”的形式出現，這樣的編排設計，目的顯而易見，重在“算法”而非“算理”，通過對短除法的學習和掌握，使學生用慣這種求“兩最”的方法，牢牢記住短除法的格式和流程，以及短除收尾的特征和“兩最”的具體計算方法。筆者通過實踐發現，用短除法求“兩最”，只要不深挖算理，只是單純學習算法，學生學起來速度驚人。運用短除法的要領是確定每一步整除的除數，根據教材的不同意圖，可采用三種方案來處理：第一種是用兩個數的共有質因數去一步步整除;第二種是用兩個數的公因數去整除;第三種是先觀察兩數，直接用2、3或5等質數去整除。三種方案大同小異，確定除數時通常是從質數2、3、5開始，這樣能迅速確定質因數。筆者在教學實踐中發現，第三種方案更加容易上手。

3.短除法有一定的靈活性。如在求取最大公因數時，每一步提取的公因數不一定非要是質數，也可以是合數，只要這個合數是待測數的公因數即可，大小不限，如果能夠一步到位找準兩數的最大公因數也未嘗不可，如果不能就一步步檢索完兩個數的所有公因數，盡可能用最少的步驟快速找完所有并列的公因數。值得注意的是，與列舉法不同，用短除法每一步找出的公因數（合數）都是互斥的，互不交叉包含。如圖1，對72和48短除時，第一次短除提取的公因數是4，第二次短除提取的公因數是6，兩數獨立互斥，各自包含一個質因數2，72和48的最大公因數就是這兩數的積：4×6=24。由此可見，短除法每次提取的公因數可以是合數，大小不限，但是一直要除到剩余因數互質為止，如上例中剩余因數為3和2，互為質數，說明短除已經觸底。

另外，在求多個（三個及以上）數的最大公因數時，方法相似，可以將三個數一并短除;但是，在求多個數的最小公倍數時，則不能一并短除，而要兩兩短除，先求出兩個數的最小公倍數，再用這個最小公倍數與第三個數短除，求出三個數的最小公倍數。如圖2、圖3、圖4。

三、兩種觀點的沖突與協調

《劉版》認為“沒有學習分解質因數也可以直接學習短除法”，增設了一個短除法的“過渡形式”，顯而易見，所謂的過渡形式就是分解因數。筆者認為這樣做有悖常理。理由如下：

其一，所謂的“過渡形式”，無非就是將一個數改寫成多個數的積，只不過偷梁換柱用“因數”代替“質因數”，達到去質因數化的目的。然而，按照算術原理，一個數只有分解成多個質因數的積，且忽略順序時，表達式才是唯一確定的。而若按照“過渡形式”寫成因數的乘積，那么表達式則變化多端。如文中所列舉的兩數24和30，如果只是分解因數亦可寫成24=1×4×6，30=2×3×5，如此一來，就會得出兩數沒有公因數的謬論。顯然，用“過渡形式”取代分解質因數是欠妥的。

其二，文中提出，采用“過渡形式”尋找的公因數是“互斥”的說法，也站不住腳。其實，利用分解質因數法求出的共有質因數確實互斥，但卻可以重復（如左短除式中重復出現的3個2）;而在做短除法的過程中，可以用非質因數去整除，這樣就會出現相互包含交叉的情況（如右短除式中的除數4和2）。

其三，文中認為教短除法，只需要教會學生記住“列舉法的公因數和互質這兩點”，也經不住推敲。“列舉法找出的公因數”是兩個數的所有公因數（可以是合數）;與利用分解質因數法找出的兩個數的共有質因數（必定是質數）是兩碼事。如72和54，列舉法找出的所有公因數是1、2、3、6、9和18，而分解質因數后找出的公因數只有2、3和3，一律為質數。在計算“兩最”時，兩數的最大公因數只能是所有共有質因數（相同數字重復計算）的乘積2×3×3=18，而非列舉法下所有公因數的乘積。

《陸版》中“棄用短除法啟用列舉法是丟卒保車”的觀點，是將兩種辦法視為互相矛盾，好像教了短除法就會削弱列舉法的影響，其實列舉法只是一種基于公因數定義的基本方法，完全是按照“兩最”概念來演繹的，通過“羅列”出所有共有因（倍）數，從而找出最小和最大，強化列舉法，重在對概念的回顧和理解，而不是機械重復查找的程序。

至于通過列舉法可能讓學生記住某些數的特性，做題時連估帶猜一下子想起“兩最”，這與方法訓練無關。其實短除法之所以只是出現在附錄中，就是考慮到算理理解上的困難，并不是否定短除法的價值。

（責編 吳美玲）