離散數學教學改革研究

惠康華 李春利

摘? 要： 離散數學的教學目的是培養學生的抽象思維和縝密概括能力，文章分析了離散數學課程教學過程中存在的一些實際問題，探索面向應用能力培養的教學改革，在關注理論知識應用的同時，注重知識之間的內在聯系，促使學生認識到嚴謹的邏輯思維、高度的抽象思維以及形式化表示在計算機科學發展過程中的作用。該教學改革可以有效地培養和提高學生理解和運用知識的能力。

關鍵詞： 離散數學; 應用能力; 教學改革; 教學方法; 抽象思維

中圖分類號：G642? ? ? ? ? 文獻標識碼：A? ? ?文章編號：1006-8228（2021）02-93-04

Abstract： The purpose of discrete mathematics teaching is to cultivate students' abstract thinking and meticulous generalization ability， in this paper， some practical problems existing in the process of discrete mathematics teaching are analyzed， and the teaching reform for the cultivation of application ability is proposed. While paying attention to the application of theoretical knowledge， it pays attention to the internal relationship of knowledge， so as to make students realize the role of rigorous logical thinking， high-level abstract thinking and formal representation in the development of computer science. The teaching reform can cultivate and improve students' ability to understand and use knowledge effectively.

Key words： discrete mathematics; application ability; teaching reform; teaching method; abstract thinking

0 引言

離散數學作為計算機科學中基礎理論的核心課程，在計算機科學中有著廣泛的應用。它不僅是許多計算機類專業課，如數據結構、操作系統、編譯原理、數據庫原理、計算機網絡、數字邏輯等課程的必備基礎[1]，而且對培養學生抽象思維能力和邏輯推理能力有著重要的作用。從某種意義上來講，沒有離散數學就沒有計算機理論，也就沒有計算機科學[2]。如何提高“離散數學”課程的教學效果一直是從事計算機科學與技術教育的教師普遍關注的重點。離散數學概念多，抽象性強，正因為如此，在離散數學的教學中往往注重理論知識的講解和邏輯推理的訓練，而忽略了對于離散數學基本理論和方法的應用，這使得該課程對計算機類專業的多數學生來說抽象難懂，從而導致學生學習的積極性和主動性不高，學習效果不明顯[3]。特別是，學生在后續的計算機專業課程學習過程中，難以做到將所學的離散數學理論知識應用于解決專業課程中實際問題，影響學生應用和創新能力的培養和提高。因此，在離散數學的教學中引入實踐性內容、加強應用能力的培養就成為課程教學中重要而迫切的任務[4]。

本文嘗試從離散數學課程的教學實踐出發，將教學目的定位于學生的抽象思維及邏輯推理能力的培養，研究和探討如何使學生對所學的知識感興趣。通過運用現代教學理念和信息資源，尋求適當的教學方法來組織實施課堂教學，激發引導學生探究科學知識[5]。

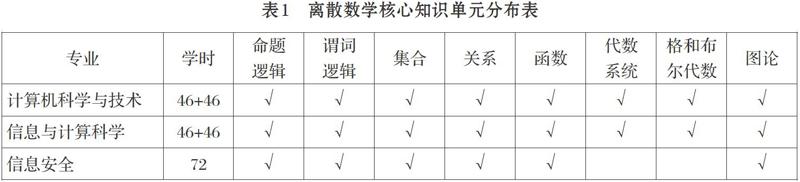
我校離散數學課程現歸屬于計算機科學與技術專業，分別在計算機科學與技術、信息與計算科學和信息安全三個專業開設，其中計算機科學與技術和信息與計算科學兩個專業的教學時數為92學時（分兩個學期完成），信息安全專業的學時數為72學時。根據專業培養目標及相應的前后續課程設置，以及計算機學院的教學實際，離散數學教學的核心知識單元分布情況如表1所示。教材選用左孝凌等主編的《離散數學》（上海科技文獻出版社出版）[6]。

1 存在的問題

⑴ 內容抽象，理論性強，學生認識不足、學習興趣不高

首先，對于計算機專業的學生，離散數學分在大一下（數理邏輯和集合論）和大二上（代數系統和圖論）兩個學期開設，此時關于專業課程只學了程序設計基礎和面向對象程序設計，而其他后續專業課程均未開設，這導致學生對離散數學基礎性和重要性的認識不足。

其次，離散數學的四大內容板塊（數理邏輯，集合論，代數系統，圖論）中，除了數理邏輯和圖論有少量簡單的應用之外，在課程教學中幾乎看不到它們在計算機類專業課程中的應用，這就容易使學生錯誤地認為離散數學對計算機類專業后續課程的學習沒什么益處，從而導致學生的學習積極性不高。

⑵ 知識點多，信息量大，內容板塊較為獨立

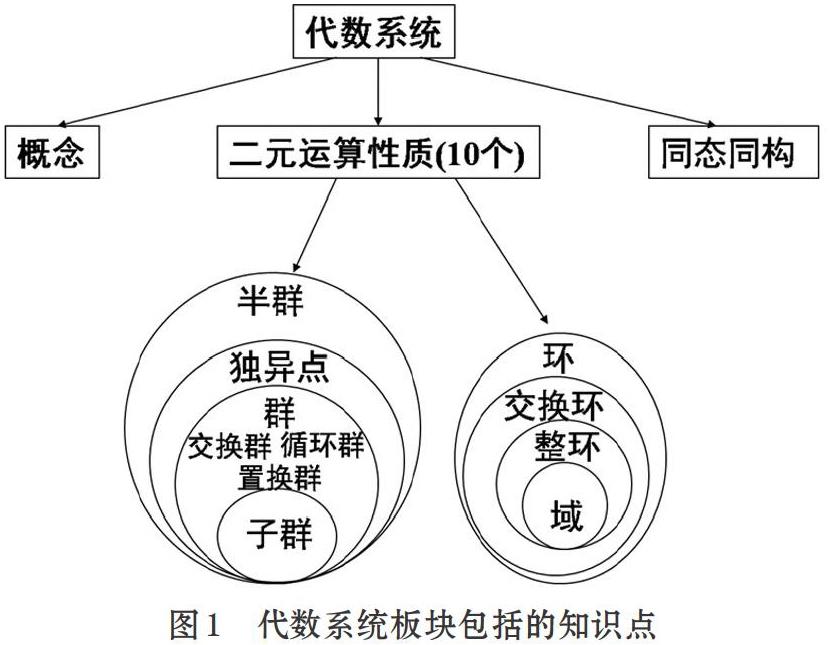
隨著每學時時間的壓縮，本來就不怎么寬裕的學時數就顯得更為緊張，面對如此多需要講授的內容，對教師和學生都是一種考驗。以代數系統板塊為例，如圖1所示，該板塊包括諸多概念和性質。以上每個知識點又包括相當多的概念、例子以及性質和結論，內容自成體系，與其他板塊聯系不強。在此情況下，如果繼續堅持普通授課模式，不能做到新舊知識結合（與數理邏輯、集合論相聯系），學生很難在規定的時間內真正理解并掌握上述繁雜的概念和性質。

2 教學方法探討

2.1 注重知識點的實際應用

離散數學是計算機類專業的專業基礎課程，其對后續相關專業課程有直接的影響。但是，離散數學課程的大多數教學內容是以抽象性很強的方式呈現的，比如代數系統和圖論等內容是安排在大二第一學期講授，此時學生只學了程序設計類專業課（程序設計基礎、面向對象程序設計），很難理解相關抽象知識的實際應用，這時可以通過一些簡單的例子說明這些知識點的應用。

比如講到圖論的Huffman樹時，在介紹完最優樹的相關概念及算法后，可以將抽象的Huffman樹應用于程序設計。

例：編寫一個將百計分a轉換成五計分的程序，分數的分布如表2所示。

如果程序設計如圖2（a）所示，是正確的，但不是最優的。衡量一個程序是否優化：①空間復雜度：程序運行時需要使用的存貯空間;②時間復雜度：程序運行時需要花費的時間。顯然地，在分數如表2分布情況下，上述程序（圖2（a））運行時間不是最優的，需要判斷315（100+95+80+40）次。那么如何設計這個程序才更合理呢？就是按Huffman樹來設計，如圖2（b）所示的程序僅需要判斷220（100+60+20+40）次。最后，鼓勵學生課下通過編程分別實現上述兩種設計思路，并對實驗結果的時間開銷進行比較分析。

2.2 強調知識點之間的聯系

離散數學教學內容板塊較多，并且各部分內容之間的彼此關聯性不強，這給學生學習課程各板塊內容以及深入理解帶來一定的困難，若能在新舊知識之間建立聯系，將有益于學生學習新的知識，并能夠牢固掌握新舊知識。

當講授代數系統板塊時，可以將代數系統和集合論知識進行聯系，集合代數是在集合定義的基礎上，研究集合運算以及集合關系，代數系統也是如此，將運算對象形成的集合連同集合上的若干個運算構成的整體看作是一個代數系統。由此可得，集合代數是代數系統的一種特殊情況，只不過代數系統研究的是更為一般的抽象對象集合上的抽象運算。通過上述引導，學生就會利用已經掌握的集合代數的相關知識去幫助理解較為抽象的代數系統。同態與同構反映了兩個代數系統之間的聯系，當講到代數系統同構時，可以將同構概念與關系和函數聯系起來，即同構映射是一種雙射函數，同構關系是一種等價關系（滿足自反性、對稱性、傳遞性）。又如，當講到子群階數的拉格朗日定理時，該定理的證明過程本質上就是基于陪集構造群的劃分的過程，陪集屬于新的知識。而劃分是集合論板塊的內容，在集合論里與劃分相關的知識包括等價關系、等價類、商集。等價關系確定等價類，等價類集合構成商集，商集為集合的劃分，反之亦然。因此，子群的陪集就是某種等價關系確定的等價類。圖3列舉了代數系統與集合論兩個板塊知識點之間的聯系，課程前后知識通過相互關聯和融合，知新并溫故，能夠有效的幫助學生理解并掌握離散數學的知識。

3 教學手段改革

隨著信息技術的快速發展，多媒體在教學過程中得到廣泛運用。離散數學的知識點繁雜抽象且課時緊張，本學期每課時由50分鐘壓縮到45分鐘，授課過程中需要運用多媒體教學手段增加課堂傳授的信息量。通過圖形、動畫、聲音等手段將抽象的知識形象生動的呈現給學生，讓學生通過多種感觀體會到形象與抽象的關系，變抽象為直觀。與此同時，在講授知識主線和要點時，對于較難理解的知識架構和脈絡關系，則需要結合板書，突出基本思想方法，引導學生思考和互動。本學期已嘗試采用的教學手段如下。

⑴ 盡量通過幻燈片演示基本概念和相對容易的性質和結論;對于較難的定理證明，做到講解清楚的同時，在黑板上把推導過程演示一遍，而不是僅用幻燈片播放一遍。

⑵ 對于圖形圖表以及文字較多的章節以幻燈片為主板書為輔，而公式較多的章節則以板書為主幻燈片為輔進行教學。

4 結束語

社會對學生運用知識和創新能力的要求越來越高，離散數學作為計算機類專業的一門核心基礎課程，在學生學習和未來工作中將產生深刻影響。本文通過開展離散數學課程教學研究，持續改進教學方法和教學手段，在關注理論知識應用的同時，注重知識之間的聯系，以期激發學生學習興趣，擴展學生思維，提高教學質量，為學生后續階段的學習和工作打下堅實的基礎。更為重要的是，通過離散數學課程改革，促使學生認識到嚴謹的邏輯思維和高度的抽象思維以及形式化表示在計算機科學發展過程中的作用。綜上所述，本文提出的教學改革措施可以有效的培養和提高學生理解和運用知識的能力。在以后的教學過程中，將進一步強化該課程與后續專業課程之間的緊密聯系，更好的發揮離散數學的作用。

參考文獻（References）：

[1] 鄭艷梅，李建江，蘆碧波等.不同學期的離散數學課程教法[J].計算機教育，2016.4：136-138

[2] 周曉聰，喬海燕.面向思維能力培養的離散數學課程教學研究[J].計算機教育，2015.15：27-30

[3] 楊淑群，李小英，黃高昂.計算機本科專業《離散數學》的教學改革與實踐[J].東華理工學院學報（社會科學版），2007.26（2）：194-197

[4] 尹波.面向計算機抽象思維能力培養的離散數學教學研究[J].計算機時代，2020.6：67-69，72

[5] 葉青，唐波.離散數學課程研究性教學模式的探索與研究[J].當代教育實踐與教學研究，2016.11：80-81

[6] 左孝凌，李為檻，劉永才.離散數學[M].上海科技文獻出版社，1982.