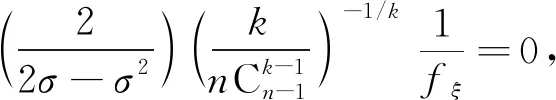一類k-Hessian方程徑向k-容許解的存在性

段對花,高承華

(西北師范大學 數學與統計學院,蘭州 730070)

1 引言與預備知識

k-Hession問題源于幾何學、流體力學等應用學科[1]. 一般地,對一個有界域Ω?n和函數u∈C2(Ω),k-Hessian算子定義為

其中:λ(D2u)=(λ1,λ2,…,λn)是Hessian矩陣D2u的特征值向量,λ1,λ2,…,λn是特征值;Sk(λ(D2u))是第k階初等對稱多項式. 顯然,k-Hessian算子是一類二階完全非線性微分算子,是Hessian 矩陣D2u所有k×k階主子式之和. 特別地,當k=1時,k-Hessian方程即退化為Laplace方程Δu=f[2-4]; 當k=n時,k-Hessian方程即退化為Monge-Ampère方程detD2u=f[5-7].

受上述結果啟發,本文研究一類k-Hessian問題:

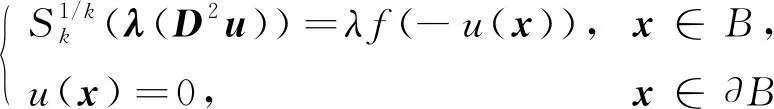
(1)

徑向k-容許解的存在性,其中λ>0是一個參數,k=1,2,…,n,B={x∈n: |x|<1}是一個單位球.

定義1[9]設Ω?n是有界開集. 對k∈{1,2,…,n},函數u∈C2(Ω)是k-容許函數當且僅當λ(D2u)∈Γk,其中Γk={λ∈n:Sk(λ(D2u))>0,k=1,2,…,n}?n.

本文總假設:

(H1)f: [0,∞)→[0,∞)是連續的.

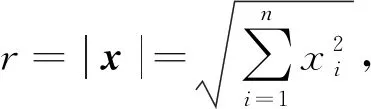
引理1[11]假設v(r)∈C2[0,1]是徑向對稱的函數,且滿足v′(0)=0,則函數u(x)=v(r),r=|x|<1是C2(B)的,且有

因此,尋找問題(1)的徑向對稱解即等價于尋找問題

(2)

的解. 由文獻[17]易知函數u∈C2(B)是問題(1)的徑向k-容許解當且僅當v(r)是問題(2)的負解.

取函數φ∈C2[0,1],做變換φ=-v,有

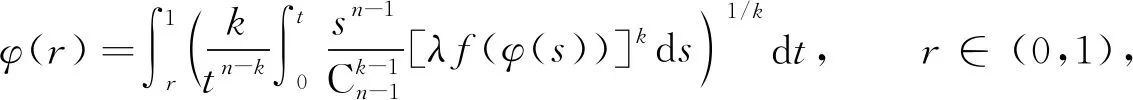
(3)

則u(|x|)=-φ(r)是問題(1)的徑向k-容許解當且僅當φ(r)是積分方程(3)的一個正解.

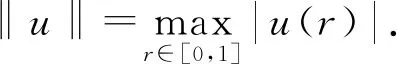
其中σ∈(0,1/2)是給定的一個正常數. 定義算子A:P→C[0,1]為

(4)

因為f: [0,∞)→[0,∞)是連續的,所以由Arzela-Ascoli定理易證A:P→P是全連續算子. 于是尋找問題(1)的徑向k-容許解即等價于尋找算子A的不動點.

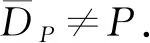
1) 若‖Au‖≤‖u‖,u∈?DP,則iP(A,DP)=1;

2) 假設存在e∈P{θ},使得對所有的u∈?DP和任意的μ>0,均有u≠Au+μe,則iP(A,DP)=0;

對給定的正實數σ,γ,定義

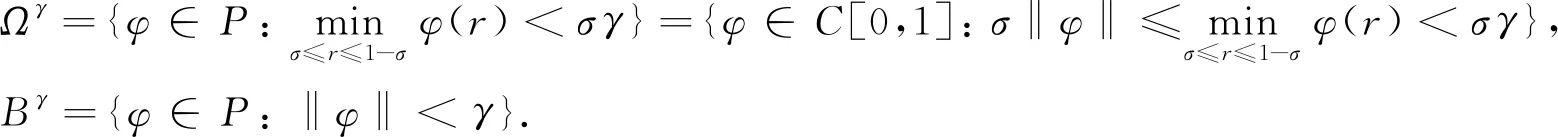
(5)

引理3[3]式(5)中定義的Ωγ和Bγ滿足如下性質:

1)Ωγ是P中的開集;

2)Bσγ?Ωγ?Bγ;

4) 若φ∈?Ωγ,則有σγ≤φ(r)≤γ,r∈[σ,1-σ].

2 主要結果

假設條件:

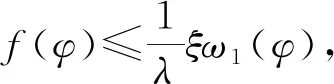
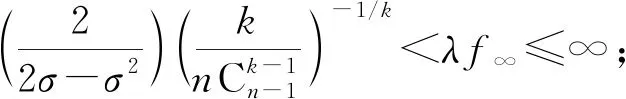
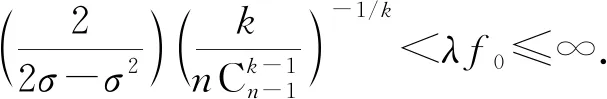
定理1假設條件(H1)～(H3)同時成立,則有:

(i) 若α<σβ,則積分方程(3)至少有一個正解φ(r),且滿足

(ii) 若α>β>σβ,則積分方程(3)至少有一個正解φ(r),且滿足

(6)

證明: 用引理2證明該結果,先證明引理2中的1),2)成立.

1) 由(H2)可知,對?φ∈?Bα和t∈[0,1],有

即‖Aφ‖≤‖φ‖,φ∈?Bα. 由引理2中1)的結論可得iP(A,Bα)=1.

2) 取e(r)=1,則e∈P{θ}. 下證φ≠Aφ+μ,φ∈?Ωβ,μ>0.

反證法. 假設結論不成立,則存在φ0∈?Ωβ和μ0>0,使得φ0=Aφ0+μ0. 由引理3中4) 可知σβ≤φ0(r)≤β. 進一步結合引理3中3),可得

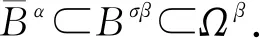
因此‖φ‖≤β,表明結論(i)成立.

為方便,記

定理2假設條件(H1)成立,若條件(H4)或(H5)之一成立,則問題(1)至少有一個徑向k-容許解.

證明: 只證明(H4)成立的情形,(H5)成立的情形類似可證.

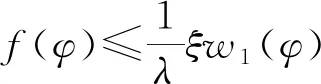
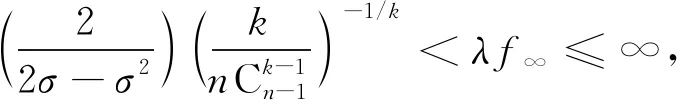
所以存在β>0,使得α<σβ,對任意的φ≥σβ,有

因此(H3)成立.

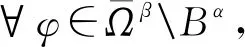
推論1假設條件(H1)成立,若

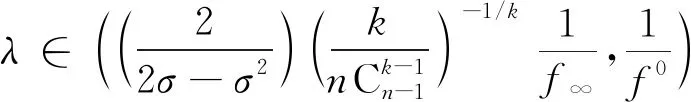
(7)

或者

(8)

成立,則問題(1)至少有一個徑向k-容許解.

證明: 設ξ=0或ξ=∞. 當fξ=∞時,