Boussinesq 方程行波解的存在性

徐園芬，章麗娜

（1.浙江萬里學院基礎學院，浙江寧波 315100；2.湖州師范學院理學院，浙江湖州 313000）

0 引 言

用于描述重力下淺水長波的傳播、一維非線性晶格中長波的傳播以及非線性弦中長波傳播的不適定Boussinesq 方程[1]

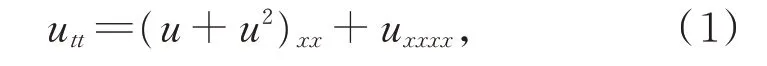
文獻［2］應用濾波和正規化技巧，得到了式（1）的六階Boussinesq 方程[1]

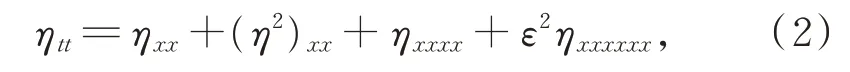
其中，ε為小參數；文獻［3］獲得了六階Boussinesq 方程弱的非局部孤立波解；文獻［4］對式（2）進行了分析和數值研究。目前尚未見與式（2）的行波系統動力學行為研究相關的報道。本文將利用平面動力系統方法的分支理論［5-13］，研究式（2）在不同參數下的精確行波解，旨在獲得與Boussinesq 方程相對應的行波系統的相圖分支，證實Boussinesq 方程存在孤立波解和周期波解。

1 與Boussinesq 方程相對應的行波方程

為研究式（2）的行波解，做以下變換：

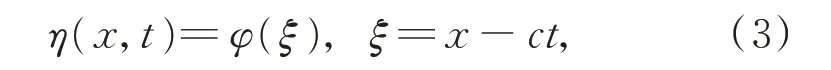
其中，c為波速。將式（3）代入式（2），并關于ξ積分4次，取積分常數為零，化簡后得

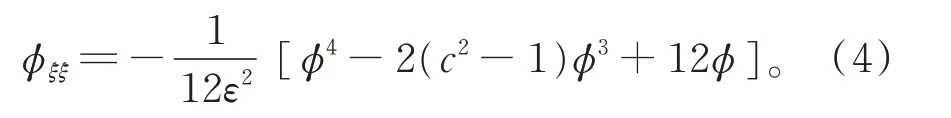
式（4）等價于以下行波系統：

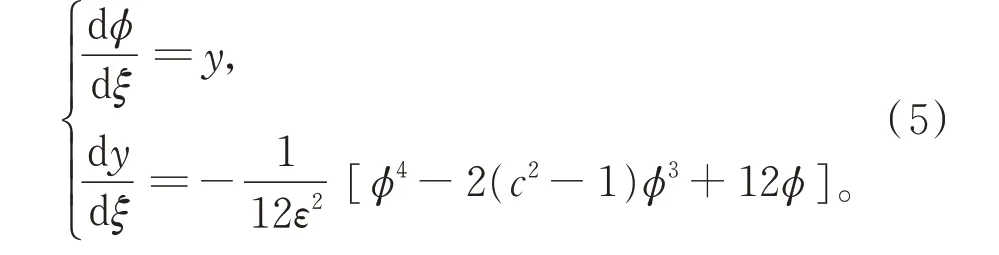
式（5）的首次積分為

下面將通過定性分析，得到式（5）的相圖分支。

2 行波系統的相圖分支

為分析行波系統式（5）的平衡點類型，令

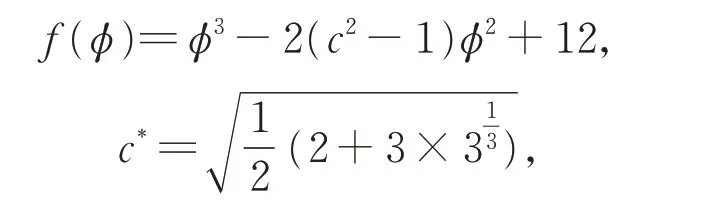
易得函數f(φ)的圖像，見圖1。

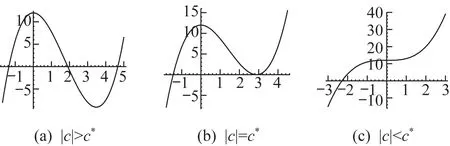
圖1 f (φ)的圖像Fig.1 The graphs of the function f (φ)

由圖1 可知，當|c|＞c*時，式（5）有4 個平衡點，分 別 為(φ1，0)，(φ2，0)，(φ3，0)和(0，0)，其 中φ1＜0 ＜φ2＜φ3；當|c|=c*時，式（5）有3 個平衡點，分別 為(φ1，0)，(φ2，0)和(0，0)，其 中φ1＜0 ＜φ2；當|c| ＜c*時，式（5）有2 個平衡 點，分別為(φ1，0)和(0，0)，其中φ1＜0。令λ(φ*，y)為式（5）的線性系統特征值，則

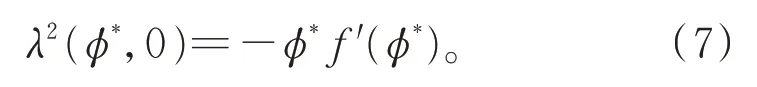
由平面動力系統理論及式（7）可知，f′(φ*)的符號和平衡點(φ*，0)的位置共同決定平衡點(φ*，0)的類型（如鞍點、中心及退化奇點等）。進一步，可得式（5）的相圖分支，如圖2 所示。

3 行波解的精確參數表達式

圖2 式（5）的相圖分支Fig.2 The bifurcation of phase portraits of formula（5）

由式（5）及其首次積分式（6），可得式（2）的某些行波解的精確參數表達式。在求解過程中將用到sn(ω，k)，cn(ω，k)，sd(ω，k)等橢圓函數以及勒讓德橢圓積分

為敘述方便，將式（6）H(φ，y)=h記為

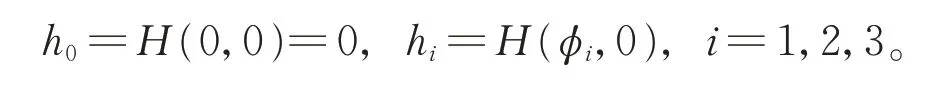
由式（6）可得

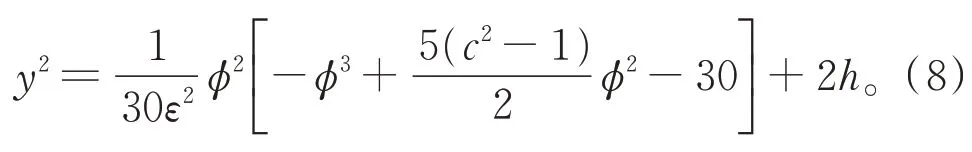
由式（5）的第1 個方程，可得

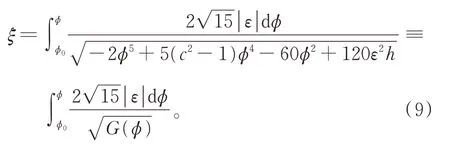
顯然，對一般的h，無法用式（9）求得行波解的精確參數表達式，因為G(φ)為五次多項式且式（9）右端為超橢圓積分。取c=2（如圖2（c）所示），有h3＜0 ＜h1＜h2，當h=0 時，式（5）為由H(φ，y)=h定義的一條周期軌道。式（8）可寫為

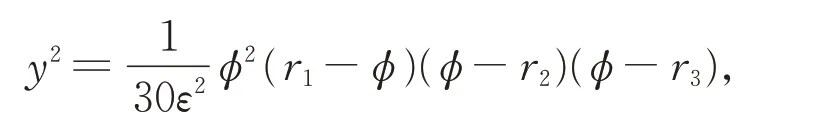
其中，r3＜r2＜φ＜r1。由式（5）的第1 個方程得

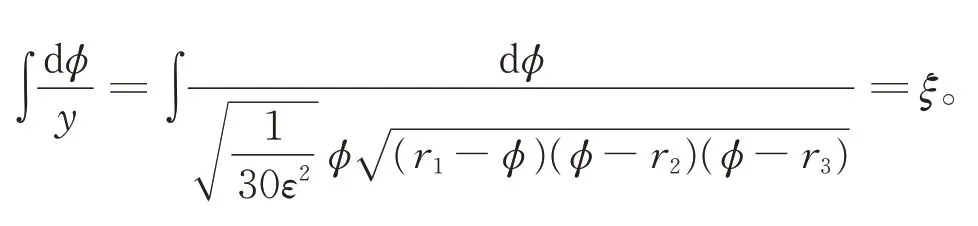
于是式（5）的周期波解為

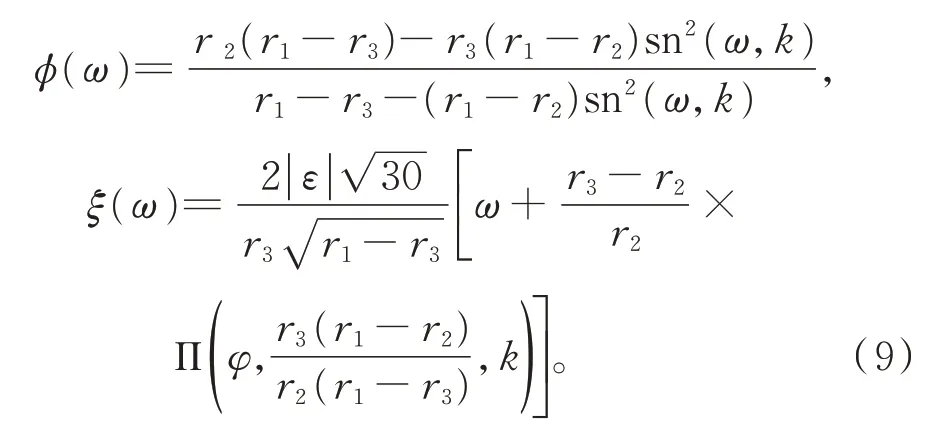
其中，ω為參數，

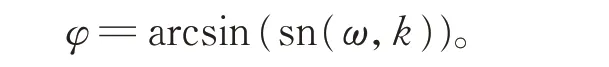
在 圖2（a）和（b）中，當h=0 時，式（5）為 由H(φ，y)=h定義的一條開軌道，式（8）變為

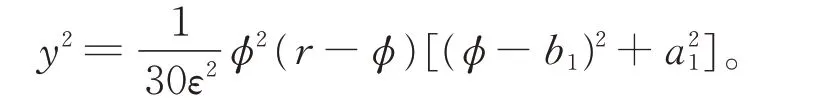
由式（5）的第1 個方程，得到式（2）的行波解參數：

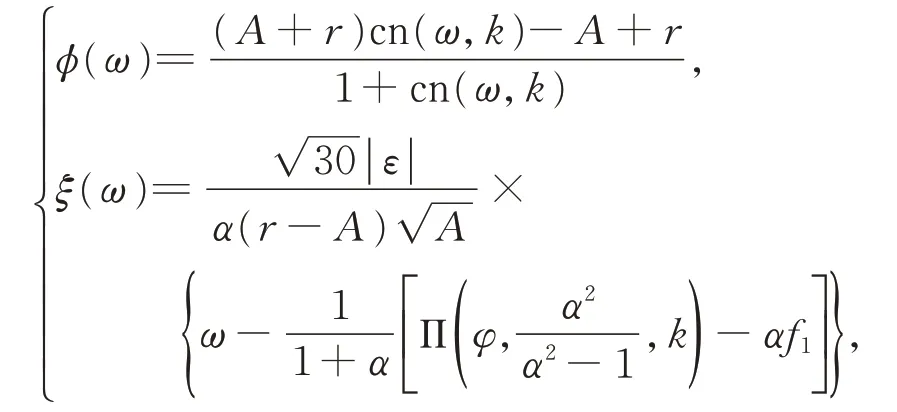
其中，ω為參數，A2=(b1?r)2+a21，

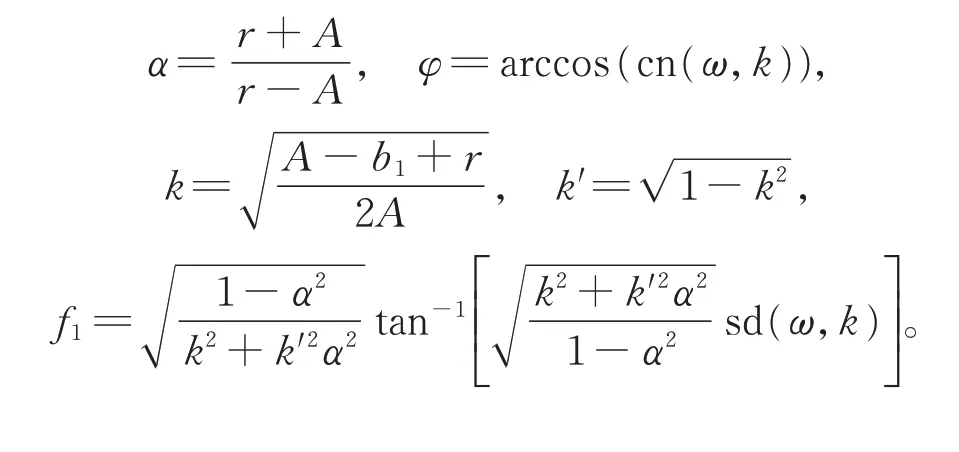
4 孤立波解和周期波解的存在性

有以下結論：

定 理1當|c| ≤c*時（如 圖2（a）和（b）所示），有

（ⅰ）當h=h1時，水平曲線H(φ，y)=h為一條同宿軌道，式（2）存在峰形光滑孤立波解；

在歷史教師看來，他所講述的歷史—故事既無用，又有用。無用之處在于，歷史似乎總是在原地打轉，歷史的經驗并不能為后人提供避免犯錯的借鑒。有用之處在于，對歷史的探究、編造和解釋本身就是人之所以為人的組成部分；對歷史的好奇心，就是對自我的好奇心；對歷史的探究就是對自我的探究。所以人類要一次又一次地講述故事，講述自我。“生命中包含了太多的空白。我們身體里十分之一是有機的生理組織，十分之九是水；生活是十分之一的‘此時此地’，十分之九的歷史課。”[2]54

（ⅱ）當0 ＜h＜h1時，水 平 曲 線H(φ，y)=h有一族周期軌道，式（2）存在一族光滑周期波解。

定理2當c*＜|c| ≤c**時（如圖2（c）所示），有0 ＜h1≤h3＜h2，則

（ⅰ）當h=h1和h=h2時，水平曲線H(φ，y)=h均為一條同宿軌道，式（2）均存在峰形光滑孤立波解；

（ⅱ）當0 ＜h＜h1和h3＜h＜h2時，水 平 曲 線H(φ，y)=h均有一族周期軌道，式（2）均存在一族光滑周期波解。

定理3當c**＜|c| ＜c***時（如圖2（c）所示），有0 ＜h3＜h1＜h2，則

（ⅰ）當h=h1時，水平曲線H(φ，y)=h為周期軌道和同宿軌道，式（2）存在光滑周期波解和峰形光滑孤立波解；

（ⅱ）當h=h2時，水平曲線H(φ，y)=h為一條同宿軌道，式（2）存在峰形光滑孤立波解；

（ⅲ）當h=h3時，水平曲線H(φ，y)=h為周期軌道，式（2）存在光滑周期波解；

（ⅳ）當0 ＜h＜h3和h1＜h＜h2時，水 平 曲 線H(φ，y)=h均有一族周期軌道，式（2）均存在一族光滑周期波解；

（ⅴ）當h3＜h＜h1時，水平曲線H(φ，y)=h有2 族周期軌道，式（2）存在2 族光滑周期波解。

定理4當|c|＞c***時（如圖2（c）所示），有h3＜0 ＜h1＜h2，則

（ⅰ）當h=h1時，水平曲線H(φ，y)=h為周期軌道和同宿軌道，式（2）存在光滑周期波解和峰形光滑孤立波解；

（ⅱ）當h=h2時，水平曲線H(φ，y)=h為同宿軌道，式（2）存在峰形光滑孤立波解；

（ⅲ）當h3＜h＜0 和h1＜h＜h2時，水平曲線H(φ，y)=h均有一族周期軌道，式（2）均存在一族光滑周期波解；

（ⅳ）當0 ＜h＜h1時，水平曲線H(φ，y)=h有2 族周期軌道，式（2）存在2 族光滑周期波解。

5 結 論

應用平面動力系統方法，得到式（5）隨波速c改變的相圖分支，當h=0 時，獲得了六階Boussinesq方程的光滑周期波解的精確參數表達式，當h≠0時，在不同波速下，證實了式（2）存在孤立波解和周期波解，且小參數ε的變化，不會改變孤立波解和周期波解的存在。獲得了光滑周期波解的精確參數表達式，證實了Boussinesq 方程存在孤立波解和周期波解。

以上結果對實驗觀察該模型的波動現象具有較好的指導作用。