素特征域上Witt 代數及極大子代數的2-局部導子

姚裕豐，王惠

（上海海事大學文理學院，上海 201306）

代數的導子指該代數上滿足Leibniz 法則的線性變換。代數上導子代數的結構對該代數的研究至關重要。SEMRL[1]最先引入代數的2-局部導子概念，并研究了2-局部導子的性質。代數的2-局部導子對該代數性質的研究有重要作用。

近年來，在特征零的代數閉域上對一些重要李代數的2-局部導子的研究取得了一定進展。AYUPOV 等[2]證明了有限維半單李代數的每個2-局部導子都是導子，且每個維數大于2 的冪零李代數均存在一個非導子的 2- 局部導子。YUSUPOV[3]證明了無限維Witt 代數的每個2-局部導子均為導子，并給出了無限維李代數的一些非導子的2-局部導子的例子。ZHAO 等[4]證明了秩為n的Witt 代數及其部分子代數的2-局部導子均為導子。

在素特征p＞3 的代數閉域F上，Witt 代數W1是變量X的截頭多項式代數的導子代數，這是WITT 在20 世紀30 年代發現的素特征域上第一個非典型單李代數。Witt 代數的每個導子均為內導子[5]。更一般地，文獻［6］確定了素特征域上Jacobson-Witt 代數的2-局部導子。本文研究Witt 代數及其極大子代數的2-局部導子。

下文第1 部分給出素特征域上Witt 代數的定義及基本性質。第2 部分證明Witt 代數的每個2-局部導子都是導子，從而將文獻［3-4］中的主要結果推廣至素特征域。第3 部分證明Witt 代數的極大子代數的每個2-局部導子均為導子。

1 預備知識

假設F是特征p＞3 的代數閉域，所有線性空間（代數）均定義在F上且是有限維的。

1.1 李代數的導子和2-局部導子

設L是域F上的李代數，則L上的導子D：L→L是L上的線性變換且滿足：

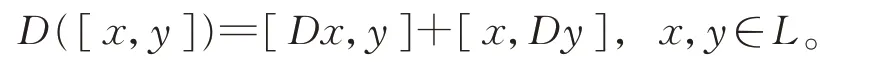
記Der(L)為L的所有導子的集合，則Der(L)將通常的換位運算作為一個李代數，稱其為L的導子代數。對于任意的x∈L，定義

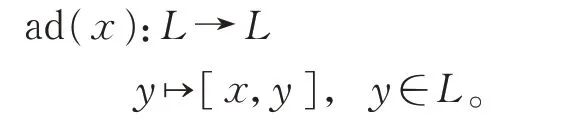
則ad(x)∈Der(L)。令

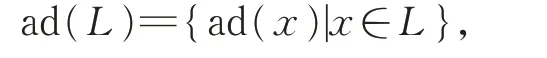
則ad(L)是Der(L)的理想。

L的2-局部導子Δ 是L上的變換（不一定是線性 變 換），且對于任意的x，y∈L，存 在Dx，y∈Der(L)，滿足

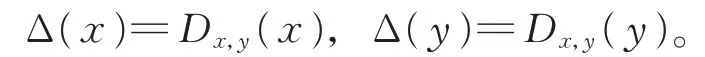
1.2 Witt 代數

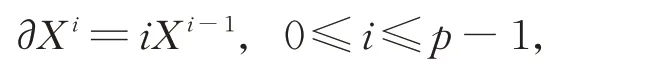
域F上的Witt 代數W1即為Α上所有導子的李代數。記ei=Xi+1?，?1≤i≤p?2，由文獻［5］，有

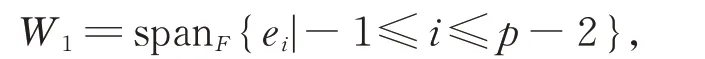
其中，W1上的李括積定義為

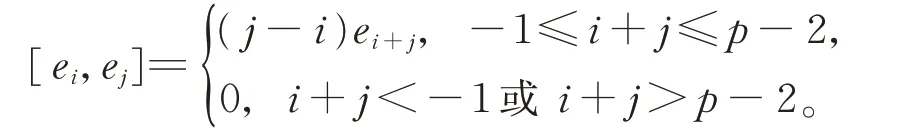
下文若不特別說明，均假設g=W1，則g有自然的Z-階化：

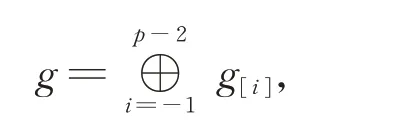
其 中，g[i]=FXi+1?，?1≤i≤p?2。 結合該階化，g有以下Z-濾過：

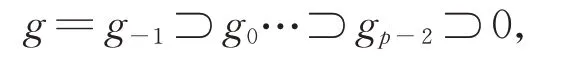
其中，

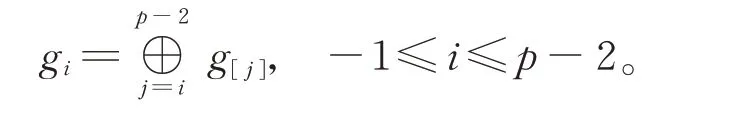
特別地，g0是g的極大子代數。

對于x∈g(或g0)，定義x在g(或g0)中的中心化子為

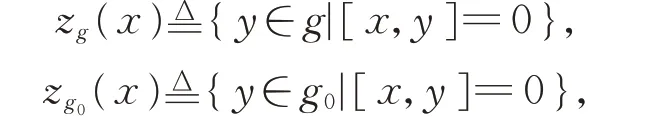
則zg(x) 是g的子代數，zg0(x)是g0的子代數。進一步，有zg0(x)?zg(x)，x∈g0。

對g及g0中的元素中心化子，有以下刻畫：

引理1[7]設g=W1是域F上的Witt 代數，x∈gigi+1。，則

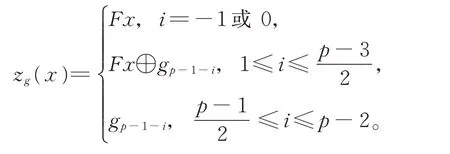
特別地，有

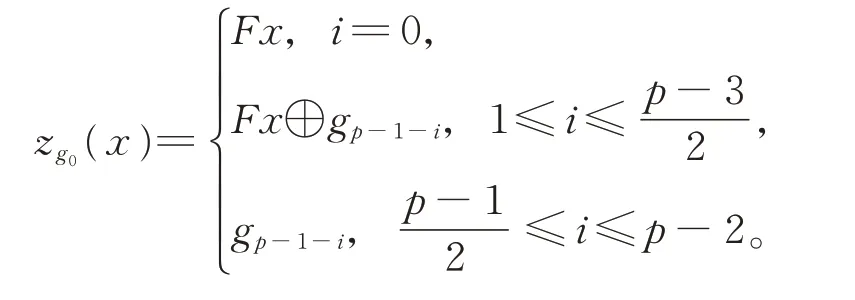
從而，有

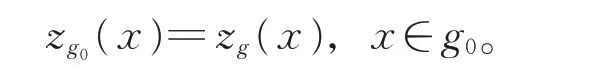
引理2[5]設g=W1為域F上的Witt 代數，則

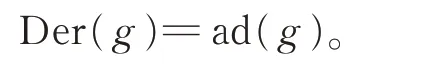
引理2 說明Witt 代數上每個導子都是內導子。

類似于引理2，以下結論表明Witt 代數g的極大子代數g0的每個導子都是內導子。

引理3設g=W1為域F上 的Witt 代數，g0=spanF{ei|0 ≤i≤p?2}是g的極大子代數，則

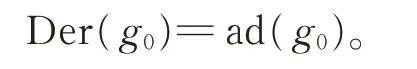
證明對于t∈Z，令

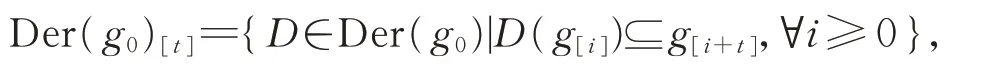
則

即Der(g0)是Z-階化代數。

下證Der(g0)的每個階化部分

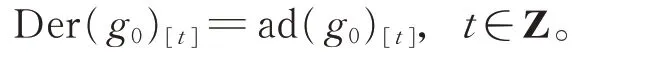
步驟1首先注意到g0的Z-階化結構，顯然有Der(g0)[t]=0，t≥p?1 或t≤1?p。

步驟2當t=0 時，任取D0∈Der(g0)[0]，設

將D0作用于[e0，e1]=e1等式兩邊，得

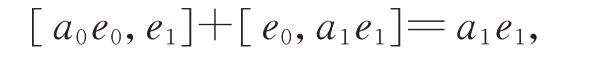
從而有a0=0。將D0作用于

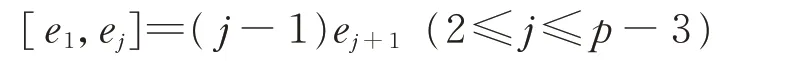
等式兩邊，得

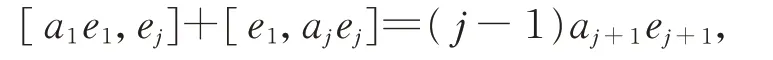
從而有

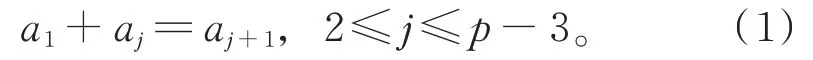
將D0作用于[e1，e4]=3[e2，e3]等式兩邊，得

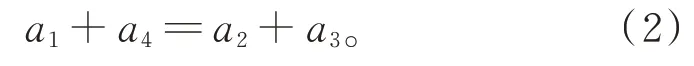
由式（1）和式（2），進一步得

因此

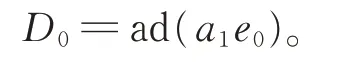
步 驟 3當 1≤t≤p?2 時 ， 任 取Dt∈Der(g0)[t]，則 有

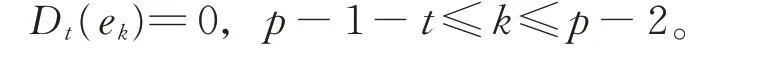
設

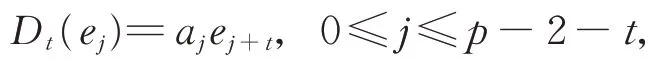
將Dt作用于

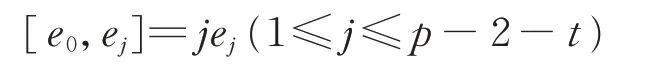
等式兩邊，得

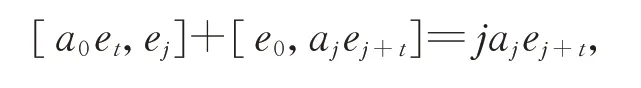
因此有

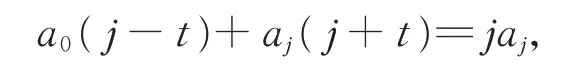
從而有

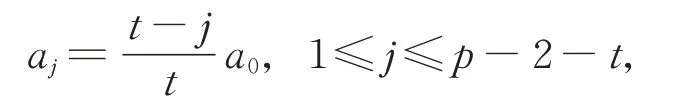
即

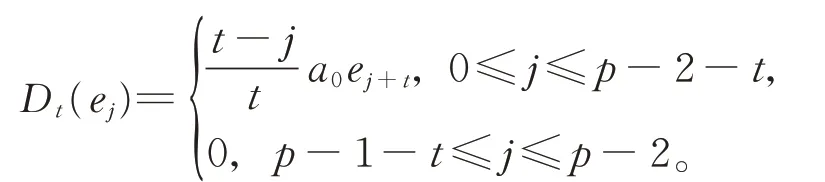
因此

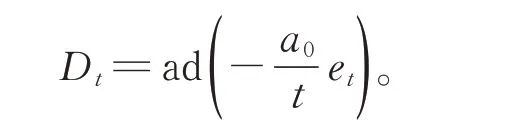
步 驟 4當 2 ?p≤t≤?1 時 ，任 取Dt∈Der(g0)[t]，則 有

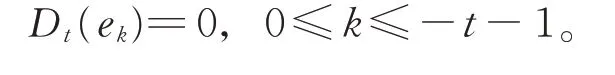
設

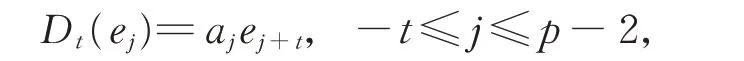
將Dt作用于[e0，e?t]=?te?t等式兩邊，得

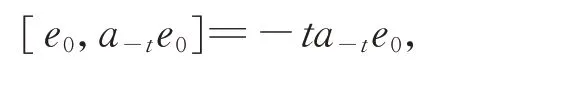
從而有

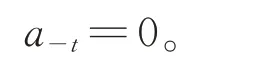
將Dt作用于

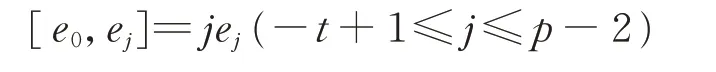
等式兩邊，得

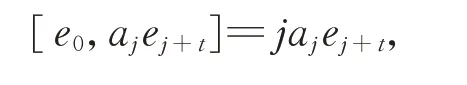
從而有aj=0， ?t+1≤j≤p?2。

因此，Dt=0，2 ?p≤t≤?1。

綜 上 所 述，有Der(g0)[t]=ad(g0)[t]，t∈Z。因此，Der(g0)=ad(g0)。

證畢。

2 Witt 代數的2-局部導子

g=W1是 域F上 的Witt 代 數。由引理2 知，若Δ 是g的2-局部導子，則對于任意的x，y∈g，存在ax，y∈g，使得

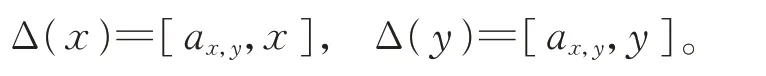
本節將證明g的每個2-局部導子均為導子。為此，需以下引理。

引理4設Δ 是g的一個2-局部導子，且

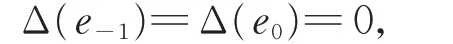
證 明任 取i∈{1，2，…，p?2}。 由 于Δ 是g的2-局部導子，因此存在ae0，ei∈g，使得

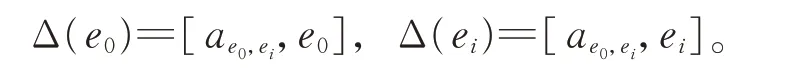
由于Δ(e0)=0，有ae0，ei∈zg(e0)。故由引理1 知，存在b∈F，使得ae0，ei=be0，有

由于Δ 是g的2-局部導子，則存在ae?1，ei∈g，使得

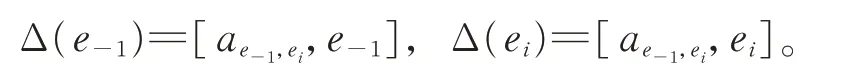
由于Δ(e?1)=0，從而有ae?1，ei∈zg(e?1)。故由引理1知，存在c∈F，使得ae?1，ei=ce?1。有

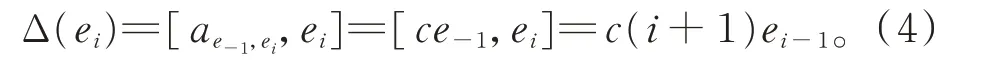
由式（3）和式（4）知，b=c=0。因此，

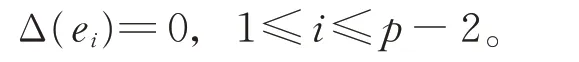
證畢。

由引理4，進一步得到

引理5設Δ 是g的2-局部導子，且

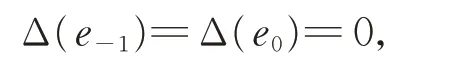
則Δ ≡0。

證明由2-局部導子的定義，顯然有Δ(0)=0。 由引理4 知，對于任意的?1≤i≤p?2，有Δ(ei)=0。

（ⅰ）l＞0。

一方面，由于Δ 是g的2-局部導子，存在ae?1，x∈g，使得

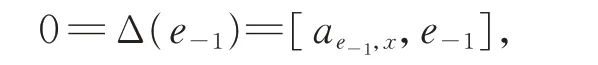
由引理1 知，存在b∈F，使得ae?1，x=be?1，故

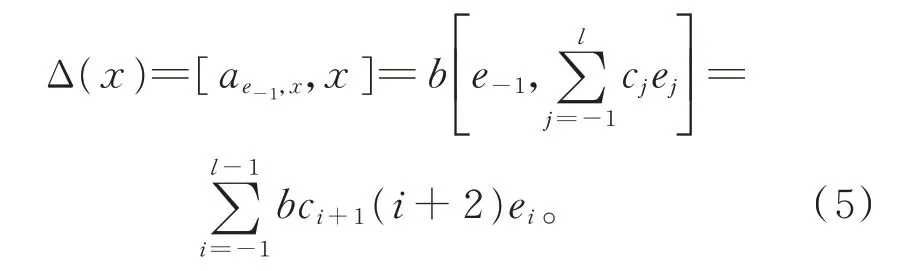
另一方面，由2-局部導子的定義，存在ae0，x∈g，使得

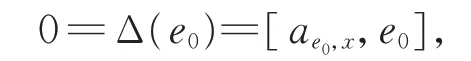
由引理1 知，存在d∈F，使得ae0，x=de0，故

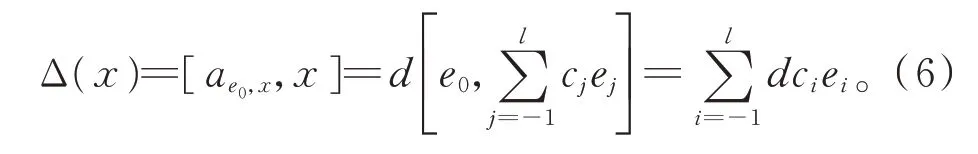
比較式（5）和式（6）的階化最高項，知d=0，由式（6）知，Δ(x)=0。

（ⅱ）l=0。

此時，x=c?1e?1+c0e0，由式（5）得

又由2-局部導子的定義知，存在ae1，x∈g，使得

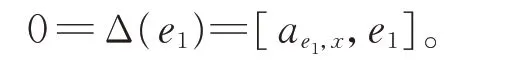
由引理1 知，存在k1，k2∈F，使得

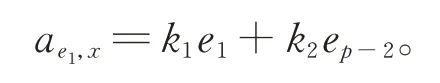
因此有

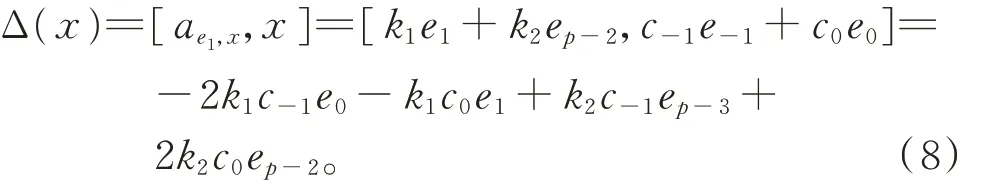
由式（7）和式（8），可得b=k1=k2=0，從而有Δ(x)=0。

（ⅲ）l=?1。

此時，x=c?1e?1，由2-局部導子的定義，存在ae?1，x∈g，使得

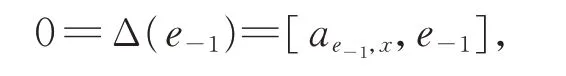
由引理1 知，存在b∈F，使得ae?1，x=be?1。因此，

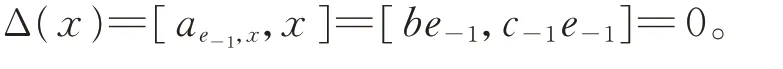
證畢。

定理1設g=W1是域F上的Witt 代數，則g的任一2-局部導子均為g的導子。

證明設Δ 是g的任一2-局部導子，則存在De?1，e0∈Der(g)，使得

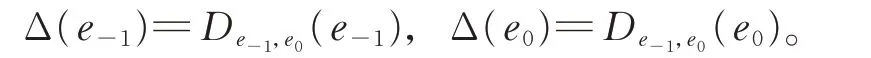
令Δ1=Δ ?De?1，e0，則Δ1是g的2-局部導子，且滿足

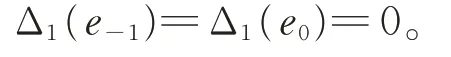
由引理5 知，Δ1≡0，即Δ=De?1，e0。因此，Δ 是g的導子。

證畢。

3 極大子代數g0 的2-局部導子

g=W1是域F上的 Witt 代數 ，g0=spanF{ei|0 ≤i≤p?2}是g的極大子代數。由引理3 知，若Δ 是g0的2-局部導子，則對任意的x，y∈g0，存 在ax，y∈g0，使 得 Δ(x)=[ax，y，x]，Δ(y)=[ax，y，y]。

引理6設Δ 是g0的2-局部導子，且

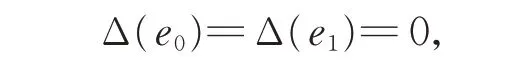
證明任取i∈{2，3，…，p?2}，由于Δ 是g0的2-局部導子，存在ae0，ei∈g0，使得

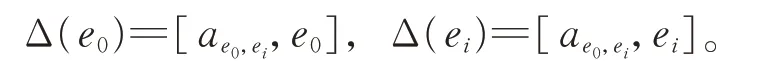
由 于Δ(e0)=0，從 而 有ae0，ei∈zg0(e0)。故 由 引 理1知，存在b∈F，使得ae0，ei=be0，有

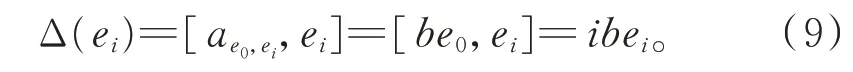
由于Δ 是g0的2-局部導子，則存在ae1，ei∈g0，使得

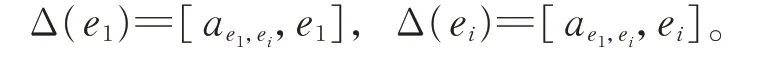
由 于Δ(e1)=0，從 而 有ae1，ei∈zg0(e1)。故 由 引理1 知，存在k1，k2∈F，使得ae1，ei=k1e1+k2ep?2，有

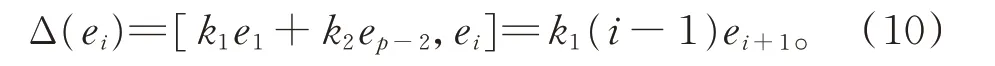
由式（9）和式（10）知，b=0。因此，

證畢。

由引理6，進一步得到

引理7設Δ 是g0的2-局部導子，且

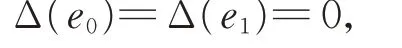
則Δ ≡0。

證明由2-局部導子的定義，顯然有Δ(0)=0。 由引理6 知，對于任意的0 ≤i≤p?2，有Δ(ei)=0。為證明本引理結論，對任意的0 ≠x=只需證Δ(x)=0。為此，令

（ⅰ）l=0。

若ck=0，1≤k≤p?2，則x=c0e0。

一方面，存在ae0，x∈g0，使 得0=Δ(e0)=[ae0，x，e0]。 故由引理1 知，存 在b∈F，使 得ae0，x=be0，有

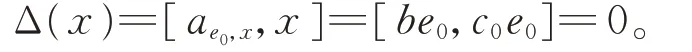
若存在1≤k≤p?2，使得ck≠0，則令

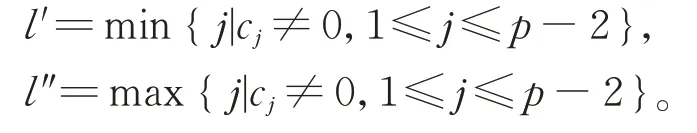
由于Δ 是g0的2-局部導子，存在ae0，x∈g0，使得

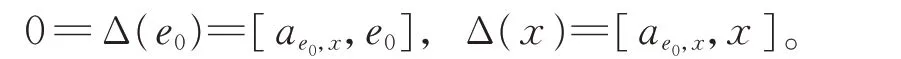
由引理1 知，存在b∈F，使得ae0，x=be0，從而有

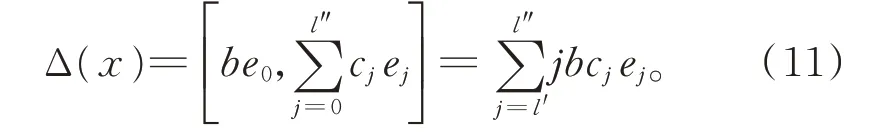
另一方面，存在ae1，x∈g0，使得

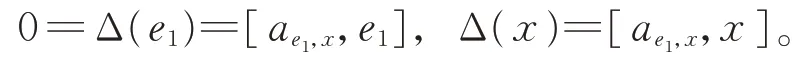
由引理1 知，存在k1，k2∈F，使 得ae1，x=k1e1+k2ep?2，從而有

比較式（11）和式（12）的最低項和最高項知，如果k1≠0，則l′=1。比較式（11）和式（12）的各項系數，可得cl″=0，矛盾，因此k1=0。如果k2≠0，比較式（11）和式（12）知，l′=l″=p?2，從而有x=c0e0+cp?2ep?2。又由2-局部導子的定義，可知存在ae2，x∈g0，有

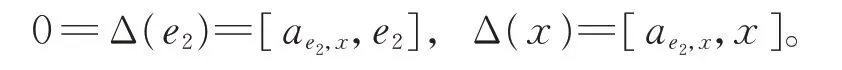
由引理1 知，存在b1，b2∈F，使得

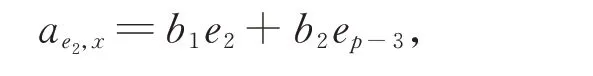
從而有

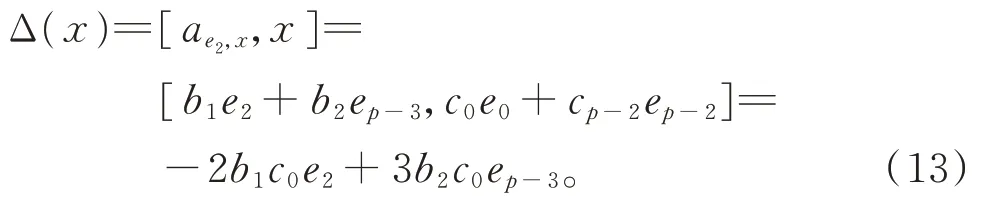
比較式（12）和式（13），可得k2=b1=b2=0。因此Δ(x)=0。

（ⅱ）l＞0。

由于Δ 是g0的2-局部導子，一方面，存在ae0，x∈g0，使得

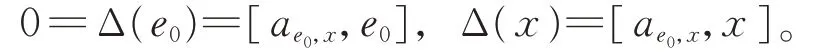
由引理1 知，存在b∈F，使得ae0，x=be0。從而有

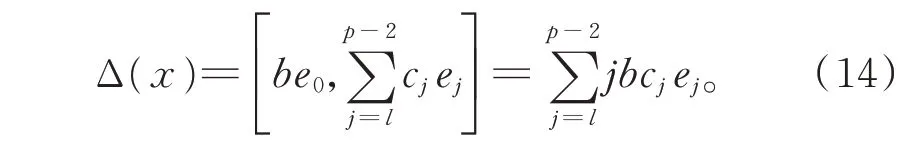
另一方面，存在ae1，x∈g0，使得

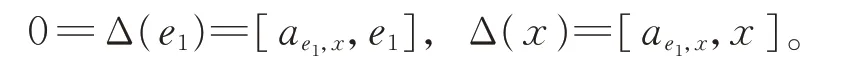
由 引 理1 知，存 在k1，k2∈F，使 得ae1，x=k1e1+k2ep?2，從而有

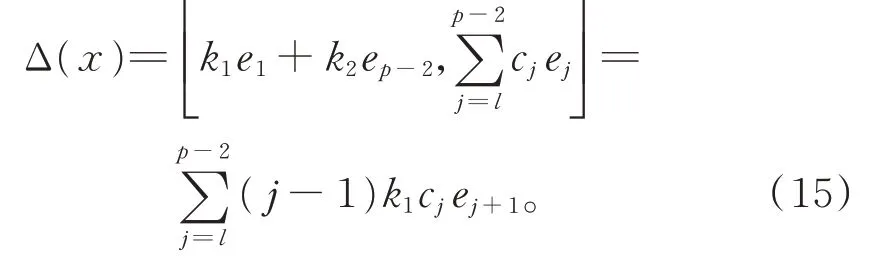
比較式（14）和式（15）的最低項，知b=0，從而有

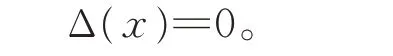
證畢。

定理2設g=W1是域F上 的Witt 代數，g0=spanF{ei|0 ≤i≤p?2}是g的 極 大 子 代 數，則g0的任一2-局部導子均為g0的導子。

證明設Δ 是g0的任一2-局部導子，則存在De0，e1∈Der(g0)，使得

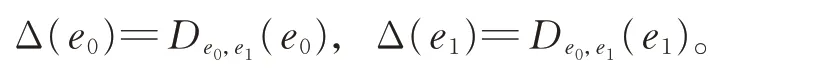
令Δ1=Δ ?De0，e1，則Δ1是g0的2-局部導子，且滿足

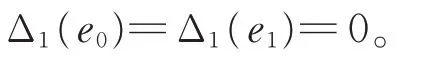
由 引 理7 知，Δ1≡0，即Δ=De0，e1。 因 此Δ 是g0的導子。

證畢。

4 結 論

討論了特征p＞3 的代數閉域上Witt 代數g及其極大子代數g0的2-局部導子的性質（引理4～引理7），得到Witt 代數g及其極大子代數g0的所有2-局部導子均為導子（定理1 和定理2）。