δ-BiHom-Jordan-李超代數的阿貝爾擴張和T*-擴張

郭雙建

（貴州財經大學數學與統計學院，貴州貴陽550025）

作為李代數的推廣，Hom-李代數的引入源于物理學和李代數的雙重需要，其概念由HARTWIG等在研究擬李代數時引入，并將其作為研究Witt 代數和Virasoro 代數變形的一部分［1-4］。

文獻［5］引入了Hom-李超代數的概念，給出了Hom-李超代數的允許分類，驗證了Hartwig-Larsson-Silvestrov 定 理 的 分 次 情 形。 隨 后，文獻［6］研究了Hom-李超代數的表示和上同調理論，計算了Witt 超代數的導子和第二上同調群。文獻［7-9］也研究了Hom-李超代數的相關性質。

BiHom-代數是一種其定義結構上的恒等式被2 個同態α，β扭曲的代數。這類代數作為一種范疇方法被引入，是對Hom-代數的推廣。文獻［10］得到BiHom-代數的基礎概念和結果。文獻［11］使BiHom-代數得以延續和發展。隨后，BiHom-李代數、BiHom-李超代數、BiHom-李著色代數和BiHom-Novikov 代數在文獻［12-14］中有更多的應用。

作為Jordan-李超代數的推廣［15］，文獻［16］引入δ-Hom-Jordan-李超代數的定義，并詳細研究其表示和T*-擴張。文獻［17］引入δ-BiHom-Jordan-李超代數的定義，并研究其表示。本文繼續研究δ-BiHom-Jordan-李超代數的性質，引入δ-BiHom-Jordan-李超代數的阿貝爾擴張，證明與任意阿貝爾擴張相關聯的表示和2-余循環。利用上同調理論和表示δ-BiHom-Jordan-李超代數的T*-擴張，證明特征不為2 的代數閉域上的有限維冪零二次δ-BiHom-Jordan-李超代數與冪零δ-BiHom-Jordan-李超代數的T*-擴張等距。另外，從上同調角度給出了T*-擴張的等價性。

1 預備知識

定義1［17］δ-BiHom-Jordan-李超代數為由向量超空間L、雙線性映射[?，?]：L?L→L和2 個線性映射α，β：L→L組成的四元組(L，[?，?]，α，β)，對任意的x，y，z∈L，有

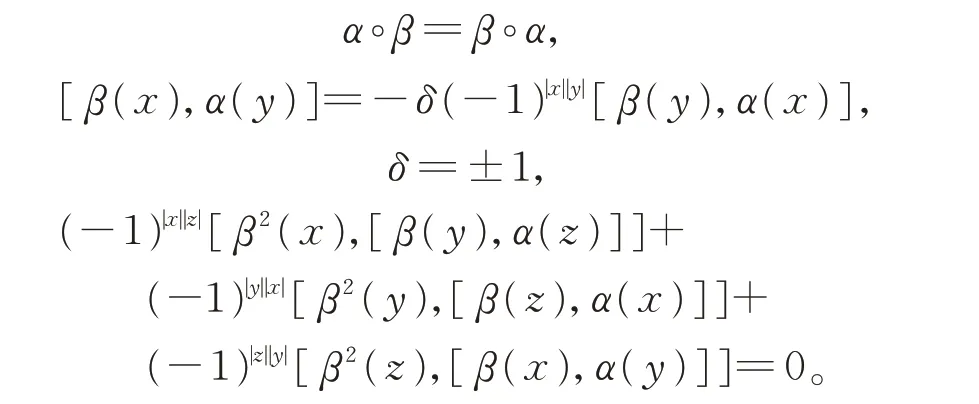
當δ=1 時 為BiHom-李超代數；當δ=?1 時 為BiHom-Jordan-李超代數。

定 義2［17］（i）若α和β為代數態射，則稱δ-BiHom-Jordan-李代數(L，[?，?]，α，β)是保積的，即對 任 意 的x，y∈L，有α([x，y])=[α(x)，α(y)]，β([x，y])=[β(x)，β(y)]。

（ii）若α和β為代數自同構，則稱δ-BiHom-Jordan-李代數(L，[?，?]，α，β)是正則的。

定 義 3［17］設(L，[?，? ]，α，β) 為 保 積δ-BiHom-Jordan-李超代數。L上的表示為四元組(M，ρ，αM，βM)，其中M是線性空間，αM，βM：M→M是2 個交換線性映射，ρ：L→End(M)是線性映射，使得對所有u，v∈L，有設(L，[?，?]，α，β)為正則δ-BiHom-Jordan-李超代數，Ck(L；M)表示L上具有M值的K-上鏈集，且是從L×…×L（k個）到M的線性映射：

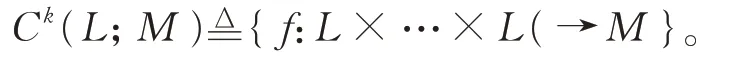
定義L上具有M值的BiHom-上鏈為K-上鏈f∈Ck(L；M)，使得其與α，β和αM，βM相容，即

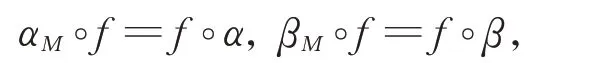
所以

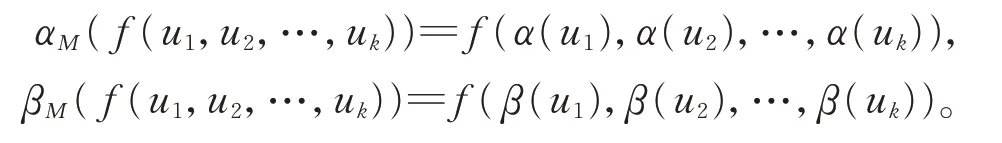
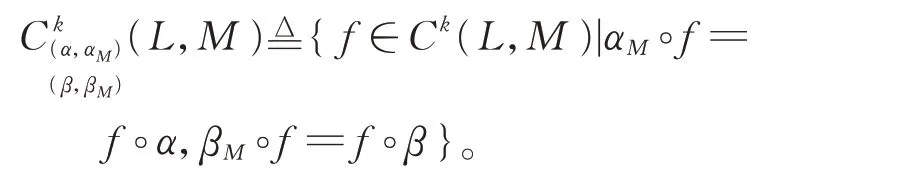
定義線性映射

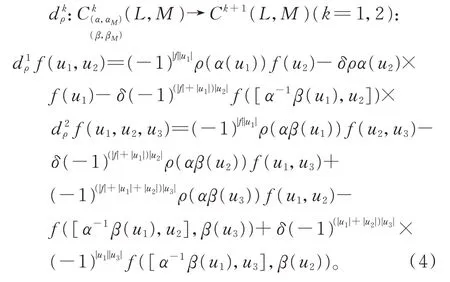
2 δ-BiHom-Jordan 李超代數的阿貝爾擴張

定 義4設(L，[?，?]，α，β)，(V，[?，?]V，αV，βV)和為δ-BiHom-Jordan 李超代數，為δ-BiHom-Jordan 李超代數的態射 。 如果 Im(i)=Ker(p)，Ker(i)=0，且Im(p)=L，則有δ-BiHom-Jordan 李超代數的正合序列：

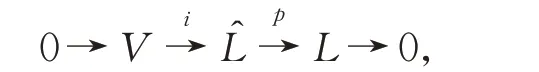
稱為L對V的擴張，用表示。如果V是?的阿貝爾理想，即對所有的u，v∈V，有，則稱V為阿貝爾擴張。?→L的截面σ由線性映射σ：L→?組 成，使得p°σ=idL，σ°α=，σ°β=。

定義5如果存在δ-BiHom-Jordan 李超代數的態射F：?，使得

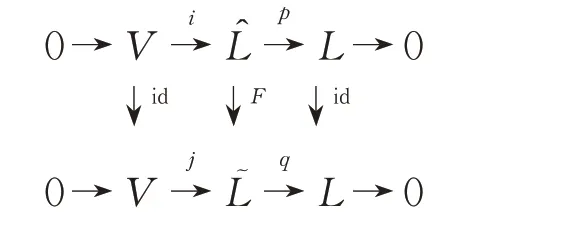
可換，則δ-BiHom-Jordan 李超代數的2 個擴張是等價的。設為L對V的阿貝爾擴張，為截面，則θ：L→End(V)的映射

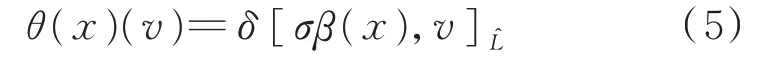
對所有x∈L，v∈V均成立。

定理1設(V，αV)和(L，α)為保積δ-BiHom-Jordan 李超代數，則(V，αV，βV，θ)是(L，α，β)的表示，且不依賴于截面σ的選取。同時，等價阿貝爾擴張有相同的表示。

證明首先，如果選擇另一個截面，則存 在u∈V，使得p(σβ(x)?σ′β(x))=β(x)?β(x)=0?σβ(x)?σ′β(x)∈V?σ′β(x)=σβ(x)+u。 注意到對所有的u，v∈V均成立，所以

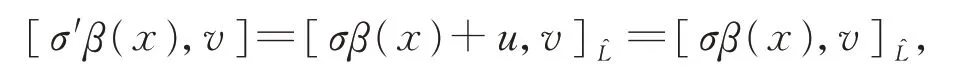
表明θ與截面σ的選取無關。

其次，證明(V，αV，βV，θ)是(L，α，β)的 表 示。對任意的x，y∈L，v∈V，有

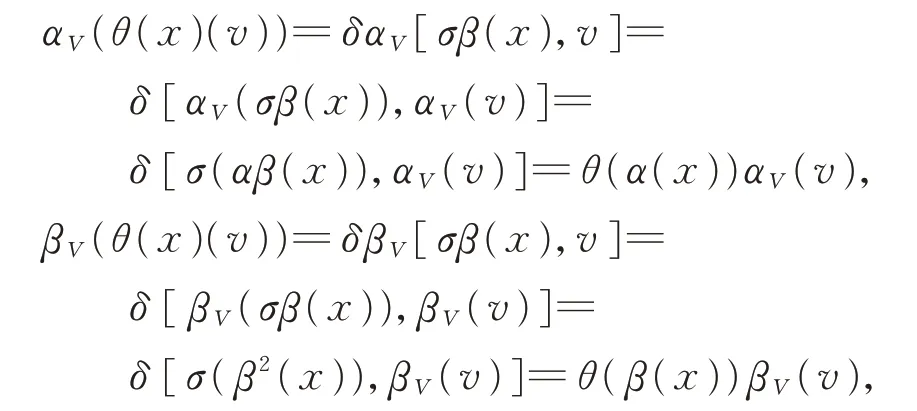
因此，可得式（1）和式（2）。

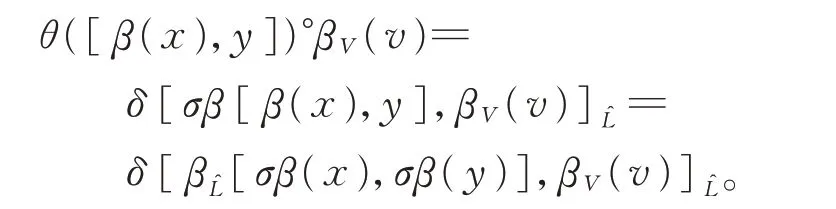
最后，

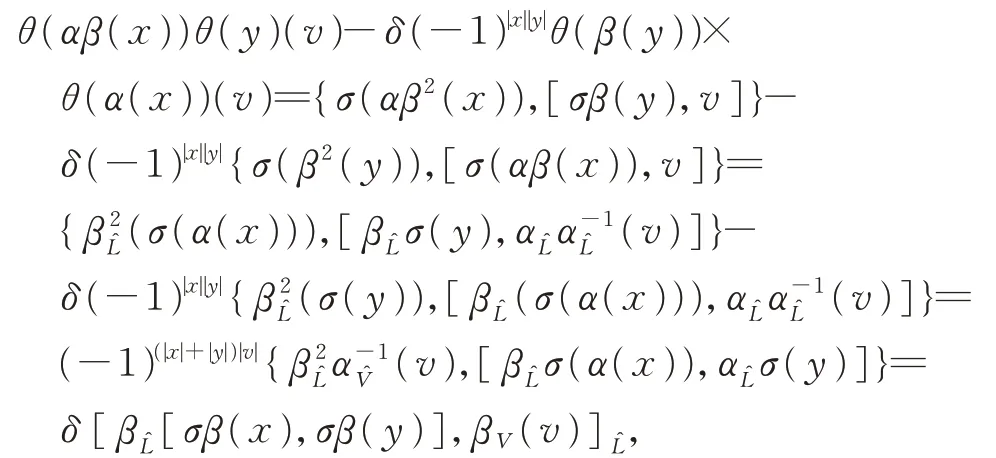
因此，可得式（3）。

接下來，驗證等價阿貝爾擴張有相同的θ。

假 設EL?和EL?是等價的阿貝爾擴張，且是 滿 足F°i=j，q°F=p的δ-BiHom-Jordan 李超代數態射。分別選取p和q的線性截面σ和σ′，則有qFσ(x)=pσ(x)=x=qσ′(x)，因此，

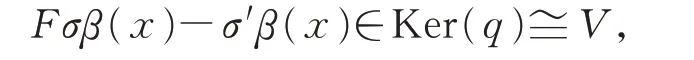
且

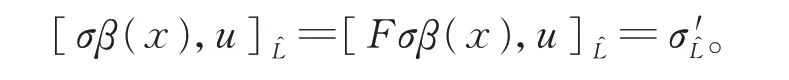
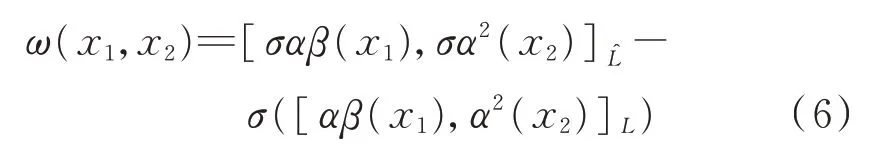
對所有的x1，x2，x3∈L成立。

定 理2設為L對V的阿貝爾擴張，則式（6）中的ω是以V為系數的L上的2-余循環，式（5）中的θ為L上的表示。

證明在式（4）中，令f=ω，ρ=θ，對任意的x，y，z∈L，有

因此，ω是2-余循環。

3 δ-BiHom-Jordan 李超代數的T*-擴張

定理3設(L，[?，?]，α，β)為δ-BiHom-Jordan李超代數，若

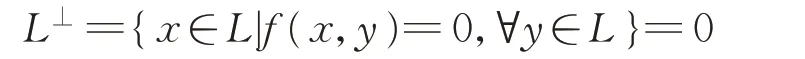
為αβ-不變量，對任意的x，y，z∈L，

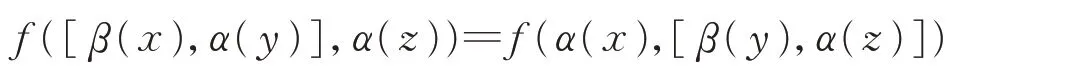
對稱，且

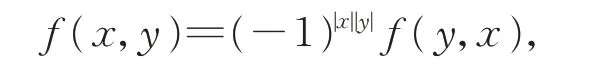
則稱L上的雙線性形式f是非退化的。

若I?I⊥，則稱L的子空間I是迷向的。

定 義 6設 (L，[?，?]，α，β) 為δ-BiHom-Jordan-李超代數，如果L具有非退化不變對稱雙線性 形 式f，則 稱(L，f，α，β)為 二 次δ-BiHom-Jordan李超代數。

設(L′，[?，?]′，α′，β′)是 另 一 個δ-BiHom-Jordan李超代數，如果存在δ-BiHom-Jordan 李超代數同構φ：L→L′，使得

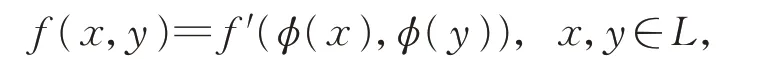
則稱2 個二次δ-BiHom-Jordan 李超代數等距。

引理1設ad 是δ-BiHom-Jordan 李超代數(L，[?，?]，α，β)的伴隨表示，考慮L的對偶空間L?，定義2 個同態為

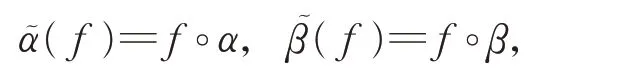
則映射π：L→End(L?)，

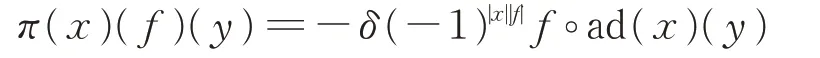
為L在上的表示當且僅當

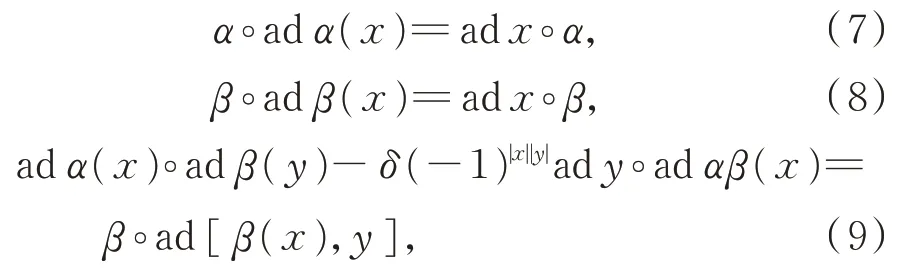
并稱π為L的余伴隨表示。

證明首先，由于

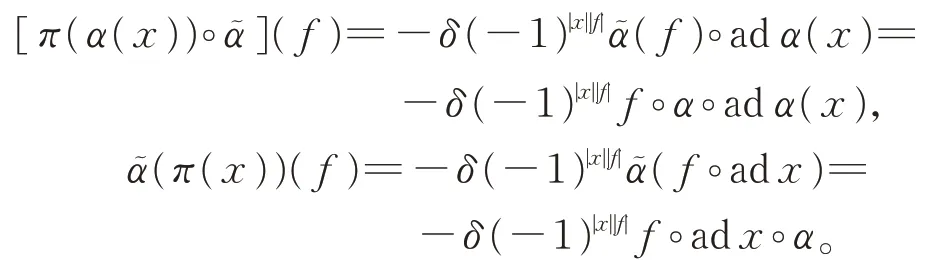
類似地，有

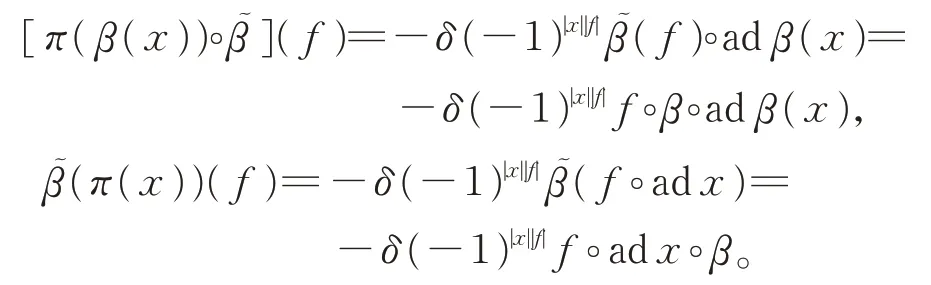
于是，

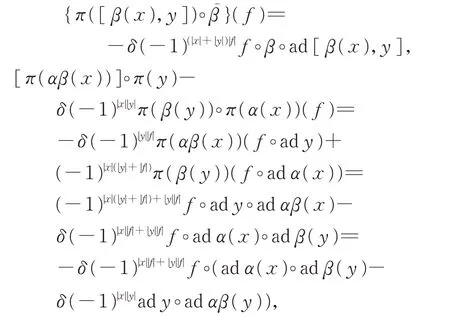
則

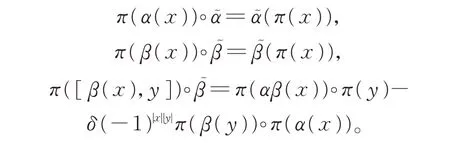
因此，π是L在上的表示。

引 理 2設 (L，[?，?]，α，β) 為δ-BiHom-Jordan-李超代數，ω：L×L→L?為雙線性映射。假設存在余伴隨表示

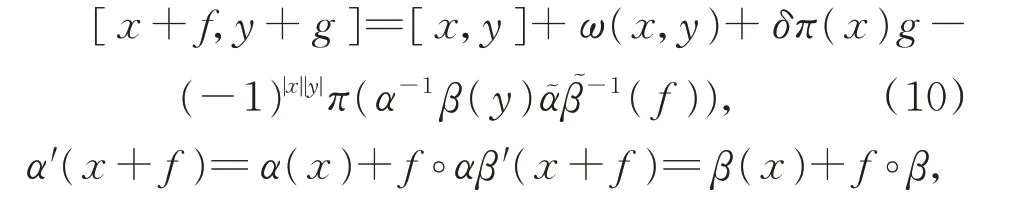
則(L⊕L?，[?，?]，α′，β′)為δ-BiHom-Jordan-李超代數當且僅當ω：L×L→L?是2-余循環。

證明對任意的x+f，y+g，z+h∈L⊕L?，有

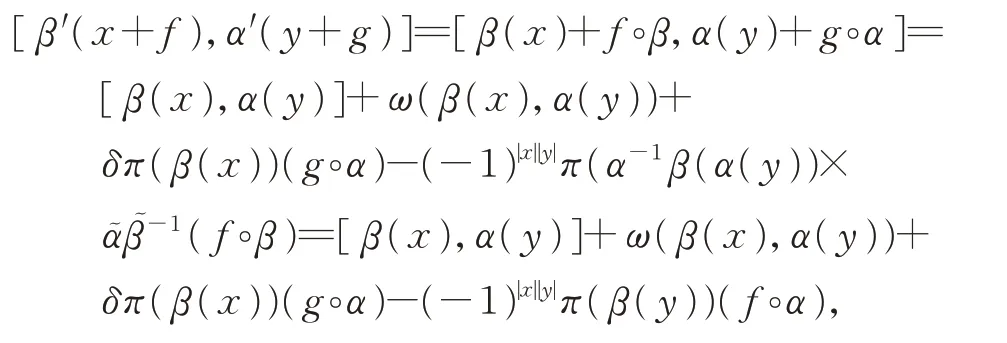
類似地，有

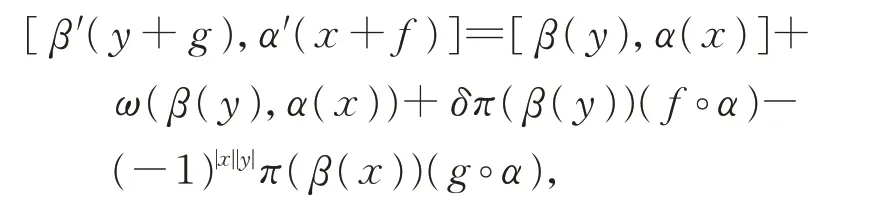
于是

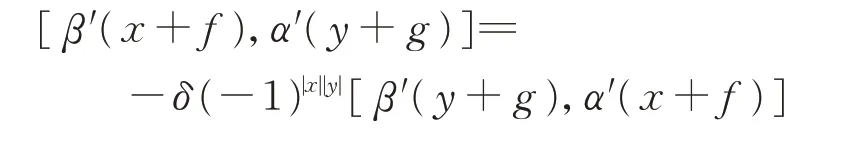
當且僅當

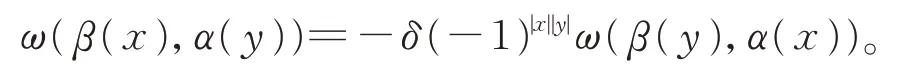
容易驗證 Jacobi 等式成立當且僅當δd?1，1ω(x，y，z)=0。

顯然，L?為(L⊕L?，[?，?]，α′，β′)的交換BiHom-理想，L與L⊕L?/L?同構。設qL在L⊕L?上具有對稱雙線性形式，對所有x+f，y+g∈L⊕L?，有

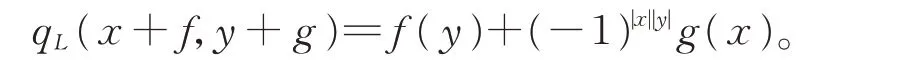
引理3設L，L?，ω，qL同前，則(L⊕L?，qL，α′，β′)為二次δ-BiHom-Jordan-李超代數當且僅當ω是Jordan 循環的，即存在x，y，z∈L，使得

證明如果x+f與L⊕L?中的元素y+g正交，那么有f(y)=0 和g(x)=0，即x=0 和y=0。因此，對稱雙線性形式qL是非退化的。

對任意的x+f，y+g，z+h∈L⊕L?，一方面，

另一方面，

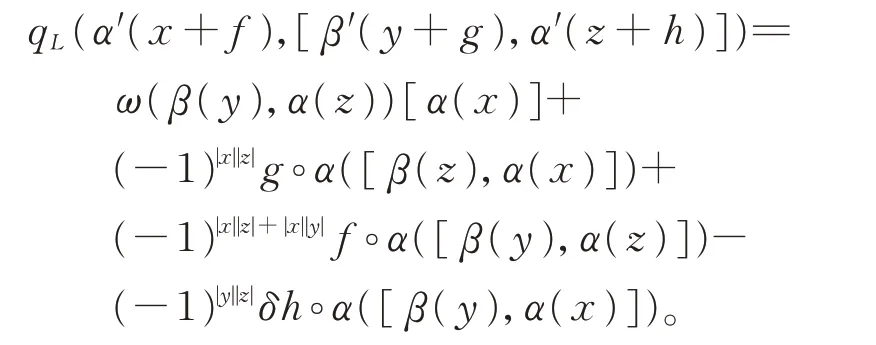
證畢。

對于Jordan 循環的2- 余循環ω，稱二次δ-BiHom-Jordan 李超代數(L⊕L?，qL，α′，β′)為L的T?-擴張，并用表示。

引理4設(L，[?，?]，α，β)為δ-BiHom-Jordan李超代數 。 定義 導出級數(L(n))n≥0：L(0)=L，L(n+1)=[L(n)，L(n)]，中 心 遞 減 級 數(L(n))n≥0：L(0)=L，L(n+1)=[L(n)，L]，稱L是可解性和冪零性的（長度為k）當且僅當存在（最小）整數k，分別使得L(k)=0 和Lk=0。

定理4設(L，[?，?]，α，β)為δ-BiHom-Jordan李超代數。

（i）如果L可解的長度為k，則T?-擴張可解（冪零）的長度為r，其中k≤r≤k+1(k≤r≤2k?1)。

（ii）如果L可被分解為L的2 個δ-BiHom-理想的直和，則平凡的T?-擴張T?0L也如此。

證明（i）首先，假設L可解的長度為k。由于意 味著由于L?是阿貝爾的，可得T?ω L可解的長度為k或k+1。

假設L冪零的長度為k。 由于設

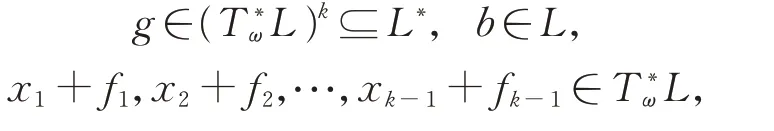
有

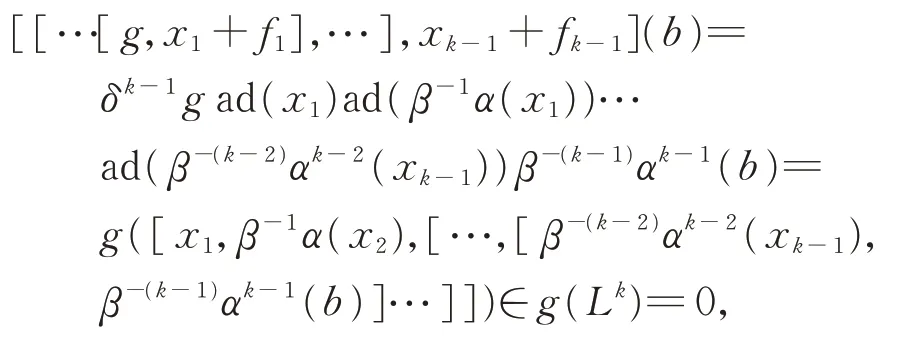
（ii）假設0 ≠L=I⊕J，其中I和J為L的2 個δ-BiHom-理想。令I?（或J?）表示在J（或I）上等于零的L?中所有線性形式的子空間。由

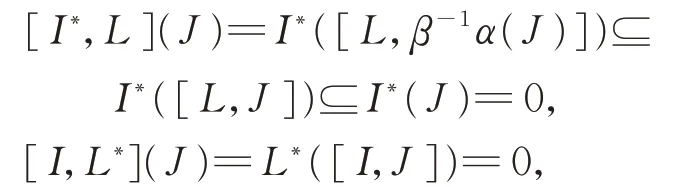
那么

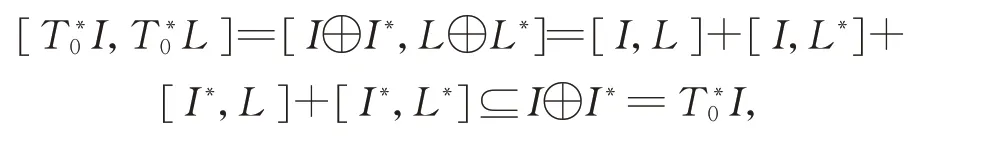
則是L的BiHom-理想，也如此。

證畢。

為證明δ-BiHom-Jordan 李超代數的T?-擴張準則，需要以下引理。

引理5設(L，qL，α，β)為維數為n（偶數）的二次δ-BiHom-Jordan 李超代數，I是L迷向的n/2 維子空間。 如果I是L的 BiHom- 理想，則[β(I)，α(I)]=0。

證 明由 于dimI+ dimI⊥=n/2+ dimI⊥=n，I?I⊥。如果I是L的BiHom-理想，那么

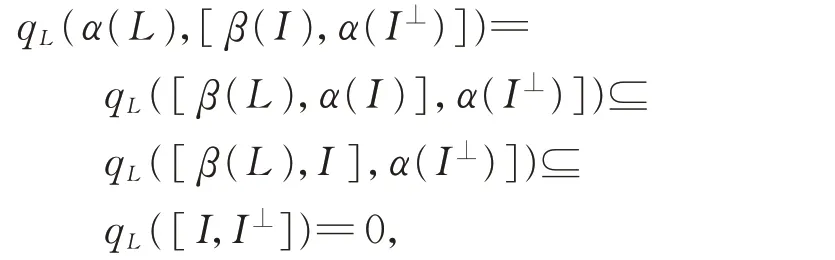
則[β(I)，α(I)]=[β(I)，α(I⊥)]?α(L)⊥=0。

引理6設(L，qL，α，β)為特征不等于2、維數為n的二次δ-BiHom-Jordan 李超代數，則(L，qL，α，β)與(，qB，α′，β′)是等距的當且僅當n是偶數且(L，qL，α，β)包含維數為n/2 的迷向的BiHom-理想I。特別地，

證明充分性。由于dimB= dimB?，dim是偶數，則dimqB(B?，B?)=0，即B??(B?)⊥和B?是迷向的。

必要性。假設I為L上一個n/2 維迷向的BiHom-理想。由引理5，有[β(I)，α(I)]=0。設和p：L→B是典范投影 。 由 于char(K)≠2，在L中取一個迷向的補子空間B0，即L=B0+I和B0?B0⊥，則有B0=B0⊥。

設滿足

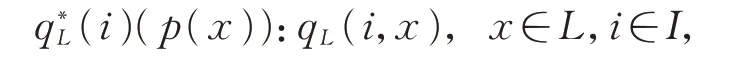
容易驗證是線性同構的。此外，具有以下性質：

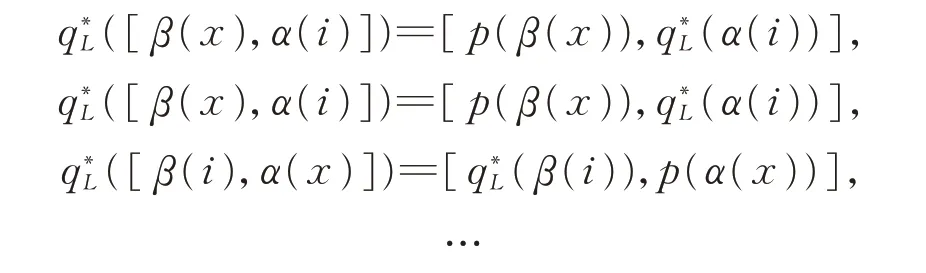
定義齊次線性映射：ω：B×B→B?，

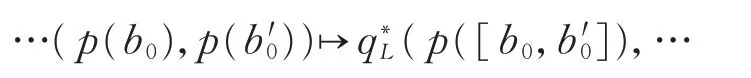
設φ：L→B⊕B?，

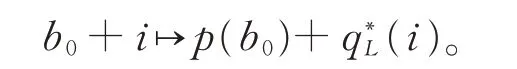
容易驗證φ是代數同構的。

下證φ是等距的。事實上，

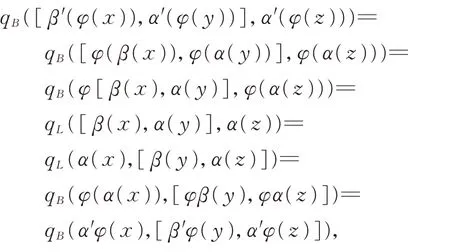
表明qB是一個非退化不變對稱的雙線性形式，因此(B⊕B?，qB，α′，β′)是 二 次δ-BiHom-Jordan 李 超 代數，從而可得B的T?-擴張，于是有(L，qL，α，β)與是等距的。

設(L，[?，?]，α，β)為δ-BiHom-Jordan 李超代數，ω1：L×L→L?和ω2：L×L→L?是2 個不同的Jordan 2-余循環。如果δ-BiHom-Jordan-李超代數的同構是BiHom-理想L?上的恒等式，并由此導出因子δ-BiHom-Jordan 李超代數上的恒等式，則稱T?-擴張是等價的。如果T?-擴張和等價，且φ等距，則稱它們是等距等價的。

引理7設(L，[?，?]，α，β)為特征不等于2 的δ-BiHom-Jordan 李超代數，ω1和ω2是2 個 不同 的Jordan 2-余循環，則有

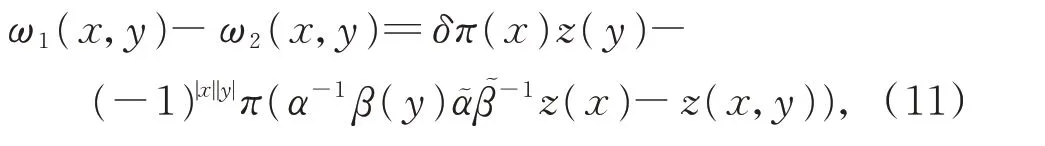
則z的對稱部分定義為

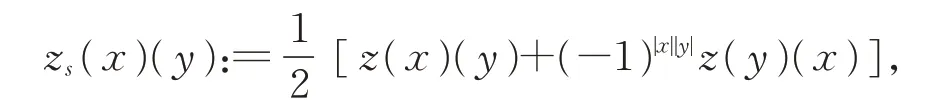
zs可誘導出L上的對稱不變雙線性形式。

（ii）與等距等價當且僅當z∈C1(L，L?)使得式（11）成立，且z的對稱部分zs等于零。

證 明（i）與等價當且僅當δ-BiHom-Jordan 李超代數的同構

滿足Φ|L?=1L?和x?Φ(x)∈L?，x∈L。

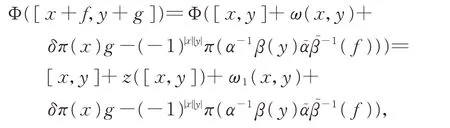
另一方面，

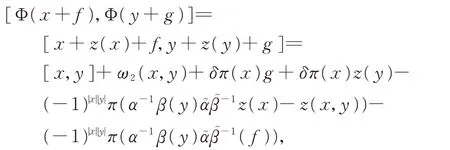
由于Φ同構，則式（11）成立。

必要性。如果存在z∈C1(L，L?)，滿足式（11），定義

滿足Φ(x+f)：=x+z(x)+f。

易證Φ是δ-BiHom-Jordan 李超代數的同構，存在x∈L，使得Φ|L?=1L?，x?Φ(x)∈L?，則與等價。

考慮由zs誘導的對稱雙線性形式

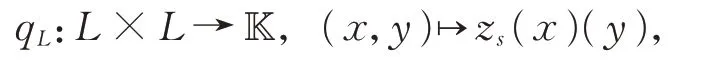
且

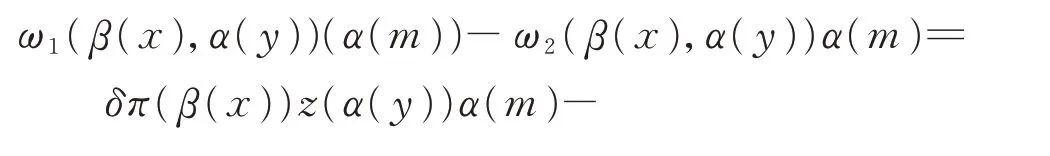
由于ω1和ω2都是Jordan 2-余循環，所以此兩個方程的右邊相同。因此

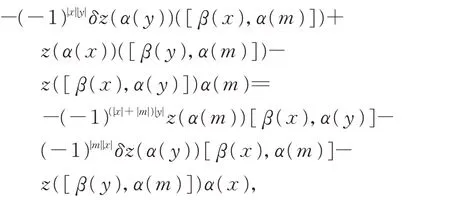
即

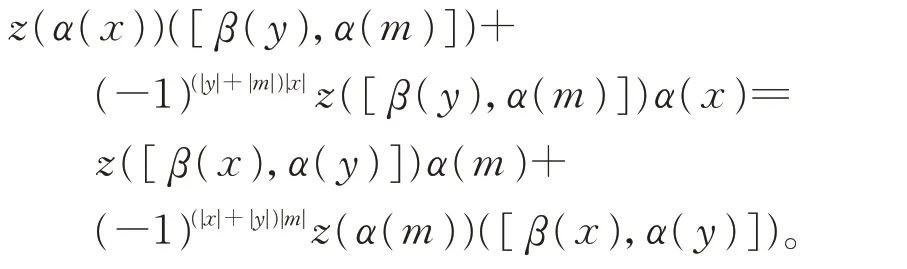
由于char(K)≠2，因此

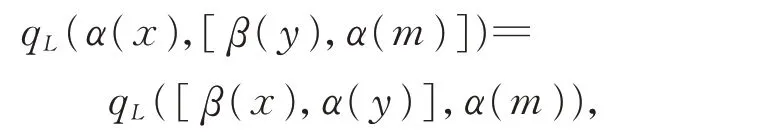
即證明了zs誘導的對稱雙線性形式qL是不變性的。

（ii）同構Φ的定義同（i），對任意的x+f，y+g∈L⊕L?，有

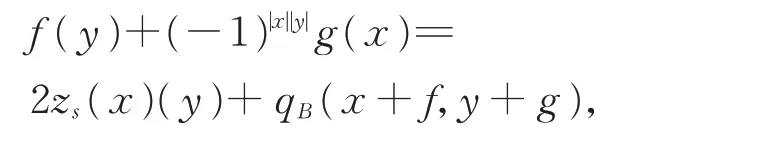
因此，Φ是等距的當且僅當zs=0。