基于拉伸特征的B-Rep→CSG 轉換算法及其應用

羅月童，韓承村，杜華，嚴伊蔓

（1.合肥工業大學計算機與信息學院，安徽合肥 230601； 2.中國科學院 等離子體物理研究所，安徽合肥 230031； 3.國家電投集團科學技術研究院有限公司，北京 100033）

0 引 言

邊界表示（boundary representation，B-Rep）法和構造實體幾何（construction solid geometry，CSG）法是使用最廣泛的2 種實體表示法，其中B-Rep 法已廣泛應用于各種商用CAD 軟件，借助商用CAD軟件強大的造型功能，用戶能方便快捷地構建三維B-Rep 模型。也有很多科學計算程序用CSG 法，如粒子輸運程序MCNP［1］、cosRMC［2］等，這是因為CSG 法具有對科學計算程序非常重要的穩定、簡單等優點。目前市場上能直接構建CSG 模型的成熟軟件較少，因此希望借助商業CAD 軟件建立B-Rep模型，然后將B-Rep 模型自動轉換為CSG 模型，以減輕建模工作量。如面向MCNP、cosRMC 等粒子輸 運 程 序 的cosVMPT［3］、MCAM［4］、McCAD［5］等軟件，這些軟件的核心功能都是將B-Rep 模型轉換為CSG 模型，即B-Rep→CSG 轉換算法。本文源于自主研發的粒子輸運COSINE 可視建模（COSINE visual modelling of particle transport，cosVMPT）軟件，旨在基于拉伸特征提升B-Rep→CSG 轉換算法的穩定性和速度，以提高cosVMPT 軟件對大規模模型的處理能力。

B-Rep→CSG 轉換問題備受關注［6］，主要有三類轉換方法：（1）半空間分割法［7］，通常利用某些面分割B-Rep 模型，基于面的半空間分割組合獲得CSG 表示，其核心是分割面的選擇，較常見的做法是從B-Rep 模型中提取分割面。文獻［8-9］利用CLoop 環構造分割面以改善分割效果，但CLoop 環的識別比較復雜。（2）交替和差分解法［10］，通過求BRep 模型的凸包并與之做布爾減運算得到差體，繼續對差體求凸包并與之做布爾差運算，如此反復循環直至差體為空，將凸包和差體組合得到B-Rep 模型的CSG 表示。（3）單元分解法［11-12］，將B-Rep 模型分解為一組單元體，用優化方法求解相關單元體組合，實現B-Rep→CSG 轉換，但此類方法通常存在過分割問題。半空間分割法因其具有直觀、易實現等優點廣受關注，其中，cosVMPT、MCAM、McCAD 采用的均為半空間分割法。

圖1 半空間分割法示意圖Fig.1 Schematic diagram of half space partition method

半空間分割法，沿一系列面將B-Rep 模型分解為若干簡單模型，然后基于簡單模型實現B-Rep→CSG 轉換，圖1 展示的為模型的分割過程。對復雜的B-Rep 模型分割量較大，通常通過造型引擎的布爾交/減運算實現分割，如MCAM 采用商業造型引擎ACIS［13］，cosVMPT 和McCAD 采用開源造型引擎OpenCascade［14］。經過多年發展，雖然ACIS、OpenCascade 引擎已較成熟，但因為布爾運算涉及復雜的數值運算，所以仍然存在布爾運算失敗的概率。 筆者在實踐中發現，開源造型引擎OpenCascade 失敗概率更高，從而降低了B-Rep→CSG 轉換算法的穩定性。因為cosVMPT 等軟件經常需要一次性轉換數萬個B-Rep 模型，中國聚變工程 實驗堆（China fusion engineering test reactor，CFETR）模型由50 000 多個B-Rep 模型組成，如圖2 所示，存在布爾運算失敗導致轉換失敗的概率，因此，在實際應用中，不得不對模型進行預處理，如將復雜的B-Rep 模型預先分解為若干簡單的B-Rep模型，這不僅需耗費大量時間，而且對用戶的CAD建模技能有很高要求，嚴重影響cosVMPT 等軟件的易用性和友好性。因此，降低B-Rep→CSG 轉換算法對布爾運算的依賴性、提升B-Rep→CSG 轉換算法的穩定性、改善相關軟件的可用性和易用性等研究具有一定的理論意義和實用價值［15-16］。

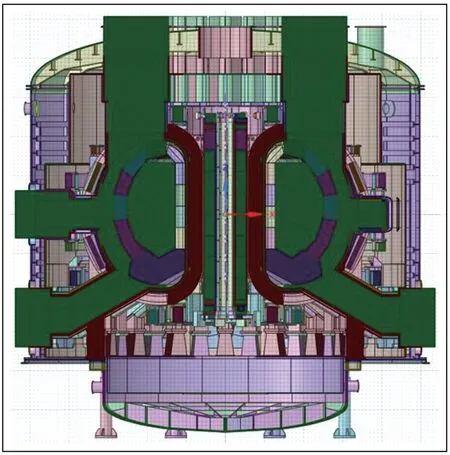
圖2 CFETR 聚變堆模型Fig.2 CFETR fusion reactor model

自主研發的cosVMPT 軟件常常用于處理裂變堆模型和聚變堆模型，圖2 為CFETR 聚變堆模型，圖3 為AP1000 裂變堆堆芯模型。筆者觀察到這類模型中存在大量掃略體，即二維圖形通過拉伸或旋轉所形成的三維對象。基于此，提出利用掃略體特點優化B-Rep→CSG 轉換：對二維圖形進行B-Rep→CSG轉換，然后將轉換映射至三維模型。因二維圖形的B-Rep→CSG 轉換不需要布爾運算，通過大幅度減少布爾運算，提升B-Rep→CSG 轉換算法的穩定性。掃略體通常包括拉伸體和旋轉體，本文以拉伸體為例探討優化B-Rep→CSG 轉換算法。拉伸特征是指單獨存在的完整拉伸體、部分拉伸體，或作為模型一部分的完整拉伸體、部分拉伸體，圖4 給出了典型拉伸特征的各種存在形式，轉換流程的關鍵是拉伸特征的識別和二維圖形的B-Rep→CSG轉換。

本文的主要貢獻包括：

（1）提出了基于拉伸特征的B-Rep→CSG 轉換算法，以減少轉換算法對布爾運算的依賴，提升了算法的穩定性；

（2）給出了拉伸特征的定義及其識別方法，解決了基于拉伸特征的B-Rep→CSG 轉換算法的關鍵問題；

（3）將所提算法集成至自主研發的cosVMPT軟件，并投入實際應用。

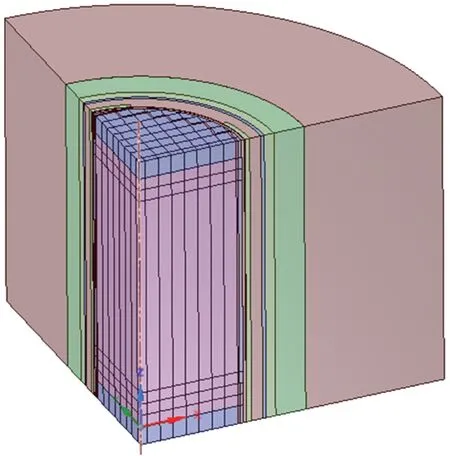
圖3 AP1000 裂變堆堆芯模型Fig.3 AP1000 fission core model

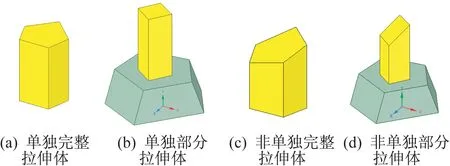
圖4 拉伸特征的各種存在形式Fig.4 Various existing forms of stretch feature

1 拉伸特征的識別

由圖4 可知，拉伸特征可看作由二維圖形沿一定方向拉伸形成的三維圖形（本文稱其為拉伸體）或其一部分。其中，由二維圖形的邊拉伸形成的面稱為拉伸面，由二維圖形的頂點拉伸形成的邊稱為拉伸邊，且所有拉伸邊均為直線，如圖5（a）所示。

雖然拉伸特征可能是拉伸體的一部分，但本文要求保留拉伸體所有拉伸邊的全部或部分。圖5（b）中，因為拉伸邊被完全切割，所以其為無效拉伸體。拉伸特征包含相應拉伸體的所有拉伸邊，可通過拉伸邊識別拉伸特征，其核心是提取拉伸特征所包含的一組拉伸邊，本文稱其為拉伸邊集。

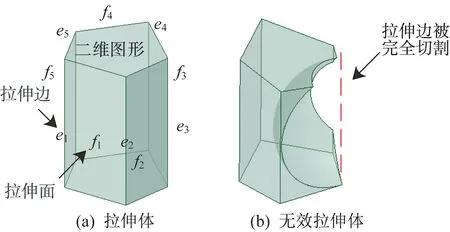
圖5 拉伸體、拉伸面、拉伸邊示意Fig.5 Schematic diagram of extruded body，extruded surface and extruded edge

1.1 拉伸邊集特點分析

為準確識別拉伸邊集，筆者對拉伸邊集進行了觀察、分析和總結，得到以下條件。

（1）相互平行性：拉伸邊集中的所有邊相互平行，拉伸邊集由一組平行邊構成。

（2）首尾相連性：如果兩條邊共享一個面，則稱這兩條邊相連。拉伸邊集中的任何一條邊與且僅與另外兩條邊相連，拉伸邊集中所有邊將形成一個首尾相連的環。

（3）方向相反性：按順時針或逆時針遍歷所有邊，按遍歷順序定義邊的方向。若拉伸邊集中的兩條邊共享一個面，則此兩條邊方向相反。

（4）唯一連接性：拉伸邊集中最多有兩條邊共享一個面。由拉伸特征的定義可知，兩條邊共享的面為拉伸特征的側面，只出現一次。

上述4 條均為拉伸邊集的必要而非充分條件，若一組邊同時滿足上述條件，則構成一個拉伸邊集。本文雖然未能給出嚴格的理論證明，但從大量的觀察、實驗和實際應用中已得到驗證。并基于上述結論設計了拉伸邊集提取算法。

對 B-Rep 模 型M=(EM，F)，其 中EM=表示模型M中所有邊的集合，F={f1，f2，…，fm}表示模型M中所有面的集合。

提取拉伸邊集算法：

（i）從EM中提取所有平行邊組：P1，P2，…，PK。因為相互平行性是拉伸邊集的必要條件，所以M的所有拉伸邊集均包含P1，P2，…，PK，每個Pi可能包含0 個或多個拉伸邊集。

（ii）利用拉伸邊集的首尾相連性、方向相反性和唯一連接性，從平行邊組Pi中提取0 個或多個拉伸邊集。

因算法（i）提取平行邊組的方法比較成熟，不再贅述，下文主要討論算法（ii）。

1.2 基于平行邊連接圖的拉伸邊集識別

因為拉伸邊集的首尾相連性與圖的簡單回路特點非常相似，所以采用基于簡單回路的算法提取拉伸邊集。提出用平行邊連接圖G=(V，EG)刻畫平行邊組各元素的連接關系，并在圖G=(V，EG)中由拉伸邊集的方向相反性和唯一連接性準確提取拉伸邊集。

平行邊連接圖G=(V，EG)的構造過程：

（2）如 果vi，vj∈V所 對 應 的 平 行 邊滿足：

則創建邊(vi，vj)∈EG；

（3）將共享面f作為邊(vi，vj) 的屬性，即令attr（vi，vj）=f。

如圖6（a）所示，B-Rep 模型垂直方向平行邊P={A，B，C，D，E，F，G，H}，其中，A-B，B-C，CD，D-A，E-F，F-G，G-H，H-E，A-F，B-E，A-E和B-F共12 對平行邊共享某個面，但A-E以及B-F的共享面為f1且方向相同，其對應平行邊連接圖如圖6（c）所示，包括8 個頂點、10 條邊及邊的屬性。

完成平行邊連接圖G=(V，EG)構建后，按以下步驟提取拉伸邊集：

（1）基于深度優先搜索的改進算法［8］求G=(V，EG)中所有簡單回路{L1，L2，…，Ln}，其中，回路Li中的節點記為{v1，v2，…，vm}，所有邊記為

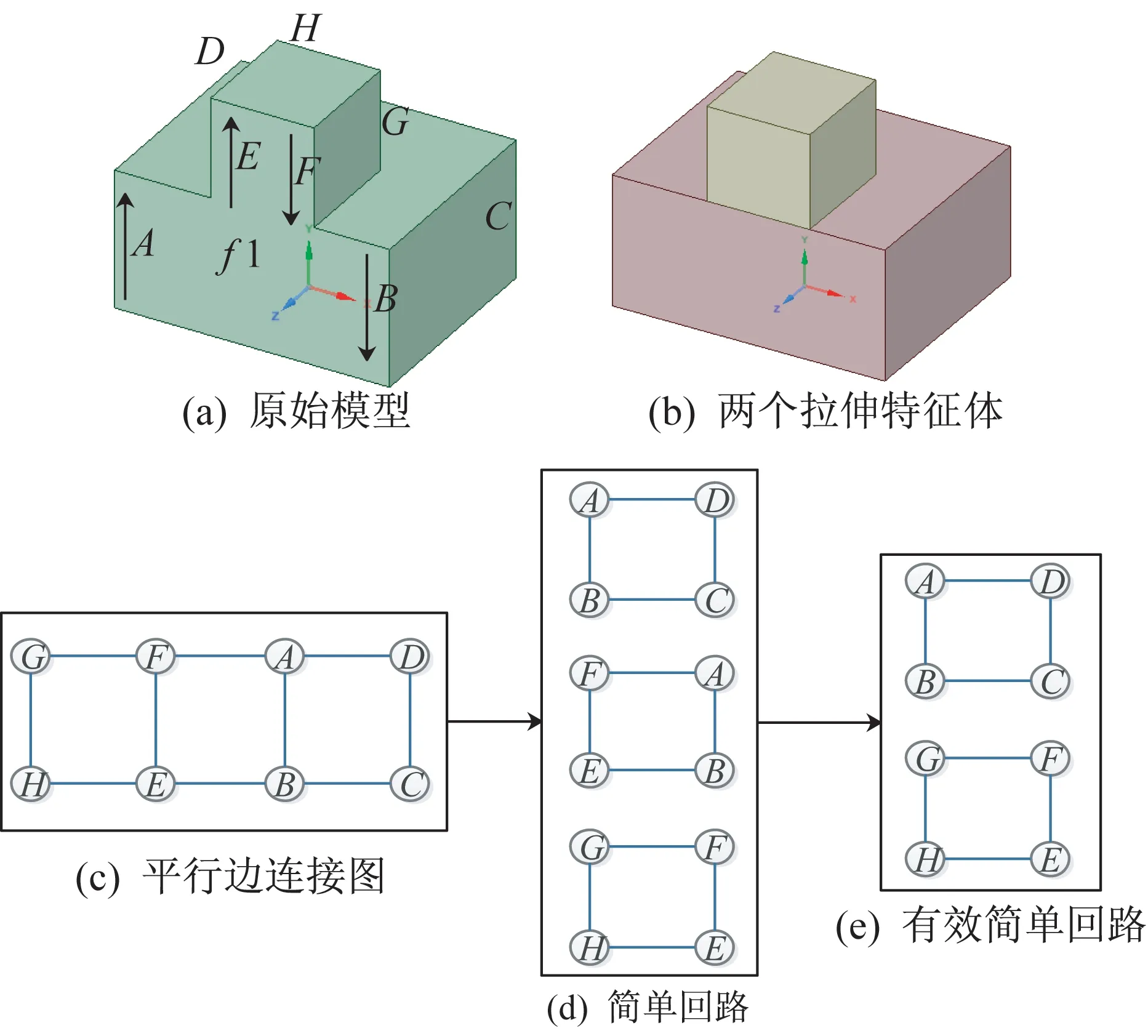
圖6 拉伸特征及其平行邊連接圖Fig.6 Stretch feature and its parallel edge connection graph

上述步驟可輸出0 個或多個平行邊集，可以證明，所輸出的每個平行邊集均滿足1.1 節中的4 個條件，因此均構成拉伸邊集。

證明過程如下：

（1）相互平行性：因為平行邊連接圖的所有節點對應模型中的一組平行邊，所以輸出的邊集為一組平行邊，滿足相互平行性；

（2）首尾相連性：因為這組平行邊對應圖中的簡單回路，所以滿足首尾連接性；

（3）方向相反性：由平行邊連接圖構建方法可知，圖中邊所連接的兩個頂點對應的平行邊方向相反，所以滿足方向相反性；

（4）唯一連接性：由提取拉伸邊集算法（ii），可排除不滿足該條件的簡單回路，因此，最終輸出結果均滿足唯一連接性。

圖6（c）為平行邊連接圖，有3 個簡單回路{A，B，C，D}、{A，B，E，F}和{E，F，G，H}，如 圖6（d）所 示，但 由 于{A，B，E，F} 中，attr(A，F)=attr(B，E)=f1，因此將其剔除，最后只保留有效簡單 回 路{A，B，C，D}和{E，F，G，H}，見 圖6（e），其分別對應圖6（b）中紅色和黃色所示的拉伸特征。

2 基于拉伸特征的B-Rep→CSG 轉換

如果B-Rep 模型M的部分或全部是一個或多個拉伸特征F1，F2，…，Fn，那么，首先將模型M分解為模型MF1，MF2，…，MFn和MR，其中，MFi表示拉伸特征Fi對應的模型，MR表示分離所有拉伸特征后的剩余部分，圖7（a）模型的分解結果見圖7（b）。然后對MFi和MR實施B-Rep→CSG 轉換獲得相應的CSG 表示CSG(MFi)和CSG(MR)，于是B-Rep 模型M的B-Rep→CSG 轉換結果可表示為CSG(M) =CSG(MR)+CSG(MFi)。

圖7 拉伸特征分解過程示意Fig.7 Schematic diagram of feature decomposition process of stretch

剩余部分MR為一般的B-Rep 模型，因此采用文獻［3］所述的B-Rep→CSG 算法。

2.1 基于環收縮的拉伸特征分離

拉伸特征是B-Rep 模型的一部分，可按各種方式與模型其余部分連接，圖8（a）中，連接處只有一個平面，較簡單，但圖8（b）中，連接處涉及多個面，較復雜。無論連接處較簡單還是較復雜，拉伸特征體MF和模型M之間的邊界都只有一個環，而文獻［9］提出基于環收縮的面殼封閉法，可依據環分離B-Rep 模型的多個部分，圖8（c）展示的為相關例題，本文用環收縮算法分離拉伸特征。

文獻［9］詳細介紹了環收縮算法，筆者在前期工作中也已實現環收縮算法［17］。本節主要討論拉伸特征體MF和模型M連接處環的提取，環提取后即可運用環收縮算法對拉伸特征體進行分類。本文稱拉伸特征體MF和模型M連接處的環為分割環。

由圖8 可知，拉伸特征邊的分割環具有以下特點：

（1）每個拉伸特征有且僅有2 個分割環，分別在拉伸特征體的兩端；

（2）分割環由拉伸面的邊組成，且不包括拉伸邊。

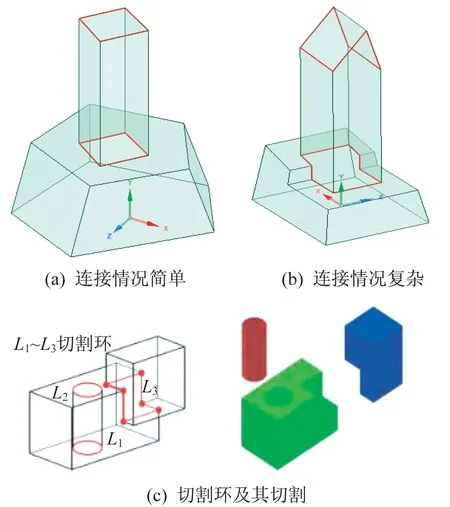
圖8 切割環示意Fig.8 Schematic diagram of cutting ring

基于以上觀察，對拉伸特征F，如果其拉伸邊面集和邊集分別為{f1，f2，…，fn}和{e1，e2，…，en}，則提取分割環的過程如下：

（1）提取所有拉伸面的邊，組成集合E=其中edge(fi)表示面fi的所有邊；

（2）去除所有拉伸邊，形成新邊集E′=E?{e1，e2，…，en}；

（3）依據E′中邊的連接關系，提取分割環。

在如圖9（a）所示的模型中，上面黃色部分為拉伸特征，其所對應的分割環如圖9（b）所示，運用環收縮分離可獲得如圖9（c）所示的2 個模型。

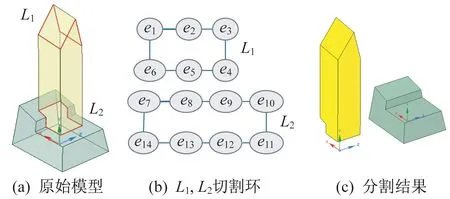
圖9 基于環搜索的分割過程Fig.9 Segmentation process based on ring search

2.2 基于拉伸特征的B-Rep→CSG 轉換

基于拉伸特征，將二維圖形沿一定方向拉伸，將三維拉伸特征的B-Rep→CSG 問題轉換為二維圖形的B-Rep→CSG 問題。如圖10 所示，在采用半空間分割法進行B-Rep→CSG 轉換時，可先對二維圖形進行轉換，然后將轉換結果映射至三維空間，如將圖10 所示輪廓面的邊映射為拉伸特征的面，再添加端面即可獲得拉伸特征的CSG 表示。本文采用半空間分解法，其拉伸特征MF的B-Rep→CSG 轉換步驟如下：

（1）獲取拉伸特征體對應的二維圖形，并對二維圖形進行B-Rep→CSG 轉換，獲得二維圖形的CSG表示，見圖10（b）。

（2）將二維圖形CSG 表達式中的邊映射至面，如直線映射為平面、圓弧映射為圓柱面，獲得兩端無界的拉伸體的CSG 表示，見圖10（c）。

（3）根據拉伸特征的端面情況，為步驟（2）所得的CSG 表達式添加端面，最終獲得拉伸特征的完整CSG 表示，見圖10（d）。

因步驟（2）可根據拉伸特征的定義直接完成映射，不再贅述。若拉伸特征的端面為單個平面，則步驟（3）可直接解決，若端面由多個面組成，則比較復雜，筆者在工程實踐中采用的是遞歸半空間分割法。因為本文的核心是拉伸特征的識別和應用，且在工程實踐中，端面多為平面，所以僅考慮端面為平面的情況，對步驟（2）和（3）不再做詳細討論。

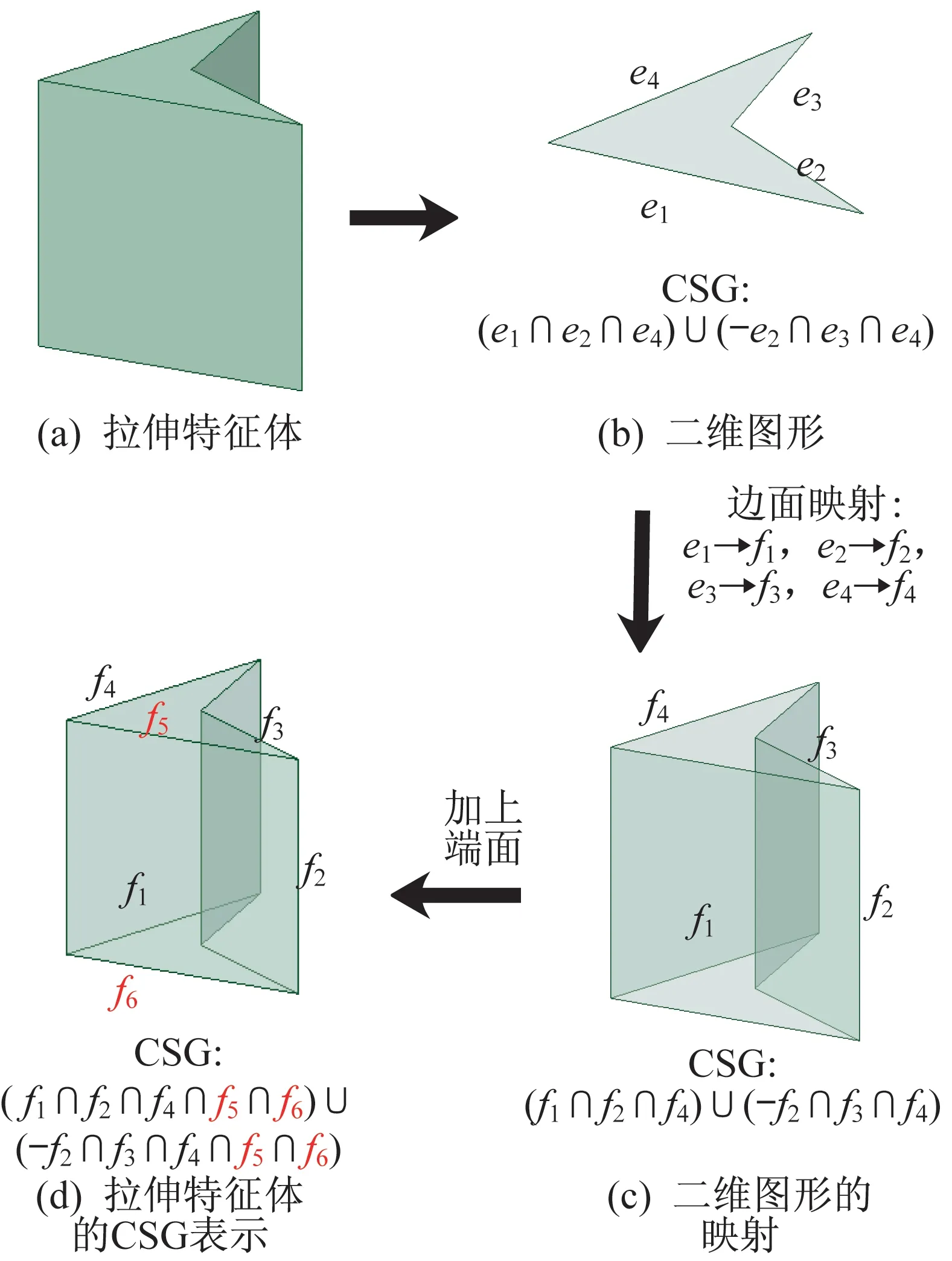
圖10 拉伸特征B-Rep→CSG 轉換過程示意Fig.10 Schematic diagram of B-Rep→CSG conversion process of stretch feature

由文獻［18］知，在半空間分割方法中，二維圖形B-Rep→CSG 轉換的難點是如何將復雜的二維圖形分解為一組簡單圖形。如果二維圖形是多邊形，則將多邊形分解為一組凸多邊形。因為將任意多邊形分解為一組凸多邊形是圖形學領域的經典問題，有大量優秀成果可以利用，本文僅考慮利用相關算法解決二維圖形的B-Rep→CSG 轉換問題。文獻［19］中的多邊形分解算法具有計算量小、分解所得的凸多邊形邊少等優點，能簡化多邊形的CSG 表示。如圖11（a）所示的復雜多邊形，用文獻［19］中的基于頂點可見的多邊形分解算法，得到如圖11（b）所示的結果，而任意分解結果如圖11（c）所示，可見文獻［19］算法的分解結果更優。

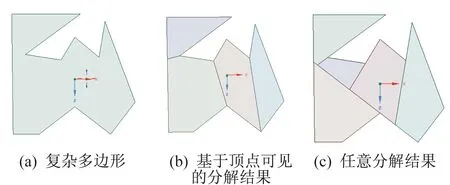
圖11 不同多邊形分解算法效果對比Fig.11 Comparison of different polygon decomposition methods

因為cosVMPT 軟件要求B-Rep 模型只能包含平面、球面、圓柱面、圓錐面和圓環面，所以當拉伸特征的拉伸面為平面或圓柱面時，所對應的二維圖形的邊為圓弧或直線。如圖12 所示，若二維圖形M2D中包含圓弧，則可通過以下方法將其轉換為多邊形，再采用多邊形分解算法（不考慮出現自交多邊形的情況）：

（1）用弦代替對應圓弧，形成多邊形P2D。

（2）記錄圓弧和弦包圍形成的二維圖形，將所有凸圓弧和凹圓弧對應的圖形分別記為{conf1，conf2，…，confn} 和{concf1，concf2，…，concfm}。

那么M2D的CSG 表示為

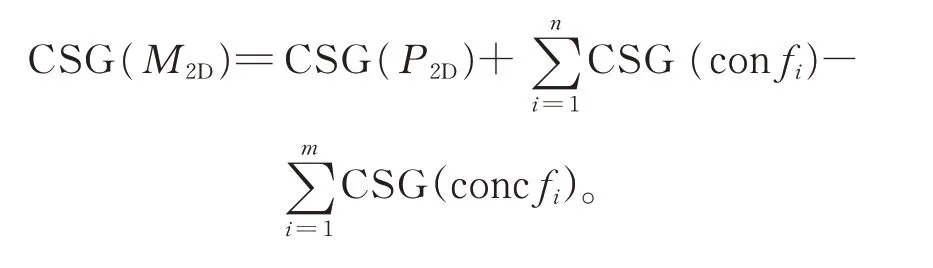
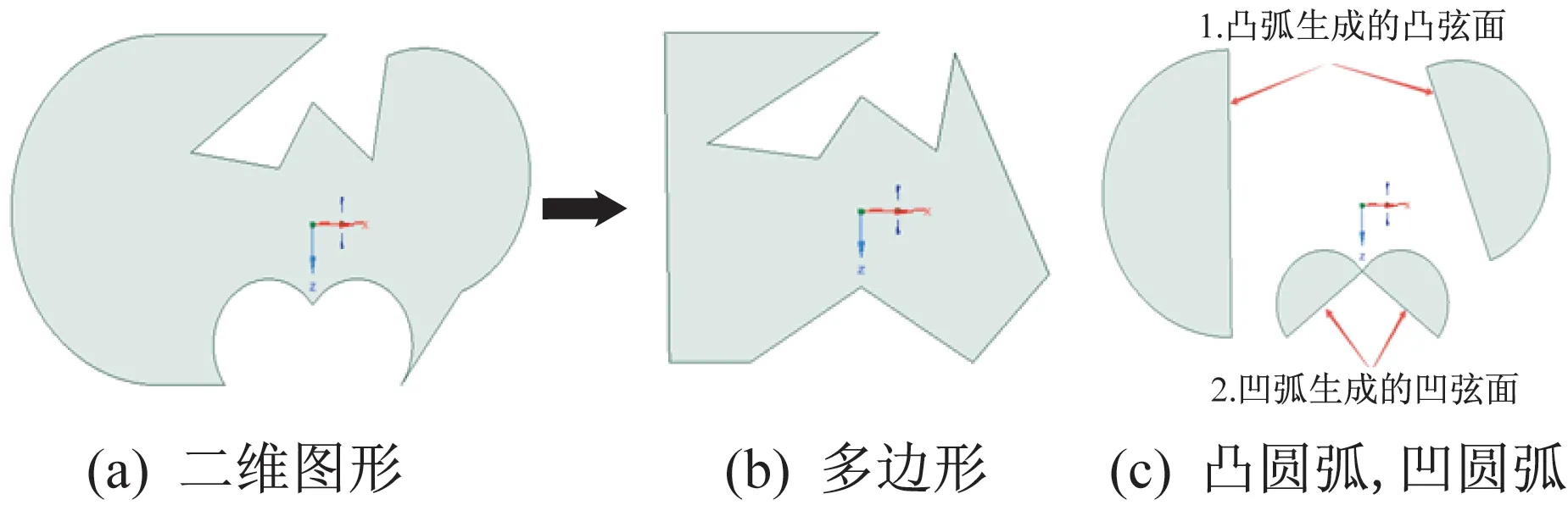
圖12 輪廓面的多邊形化過程Fig.12 Polygonization process of profile

3 實驗與應用

本文算法已應用于我國自主核能設計軟件包COSINE 的輔助建模cosVMPT 軟件，其主界面如圖 13 所示。 該軟件基于開源造型引擎OpenCascade 7.3.0，在windows 平 臺 采 用visual studio 2017 開發。 本文中的所有實驗均基于cosVMPT 完成。

圖13 cosVMPT 主界面Fig.13 The main interface of cosVMPT

首先由簡單到復雜構造3 個模型，見圖14 中的（1）、（2）和（3）。分別對模型進行測試，并對采用本文算法前后的轉換時間和轉換效果進行比較，見表1 和圖14。因為半空間分割法B-Rep→CSG 轉換的核心是分解復雜模型，所以圖14 未采用最終的CSG表達式，而是以分解結果表示轉換效果。

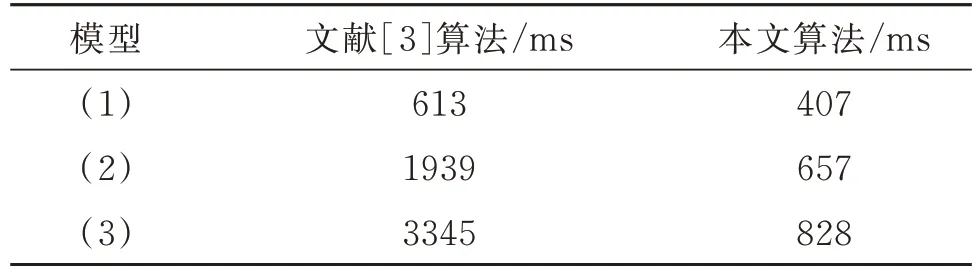
表1 轉換時間比較Table 1 Time comparison of conversion

由圖14 可知，本文算法的分解結果更簡潔或其CSG 表示更簡潔。如本文算法可將模型（2）分解為4 個子模型，而半空間分割法則將模型（2）分解為9個子模型，且本文算法分解結果更符合模型的特點，即具有更強的語義性；雖然用半空間分割法分解模型（1），子模型數更少，但其分解結果的CSG 表示更復雜，需要添加輔助分割面。由表1 可知，在轉換時間上，本文算法也具明顯優勢，3 個模型均提速30%以上，且模型越復雜，提速效果越明顯。

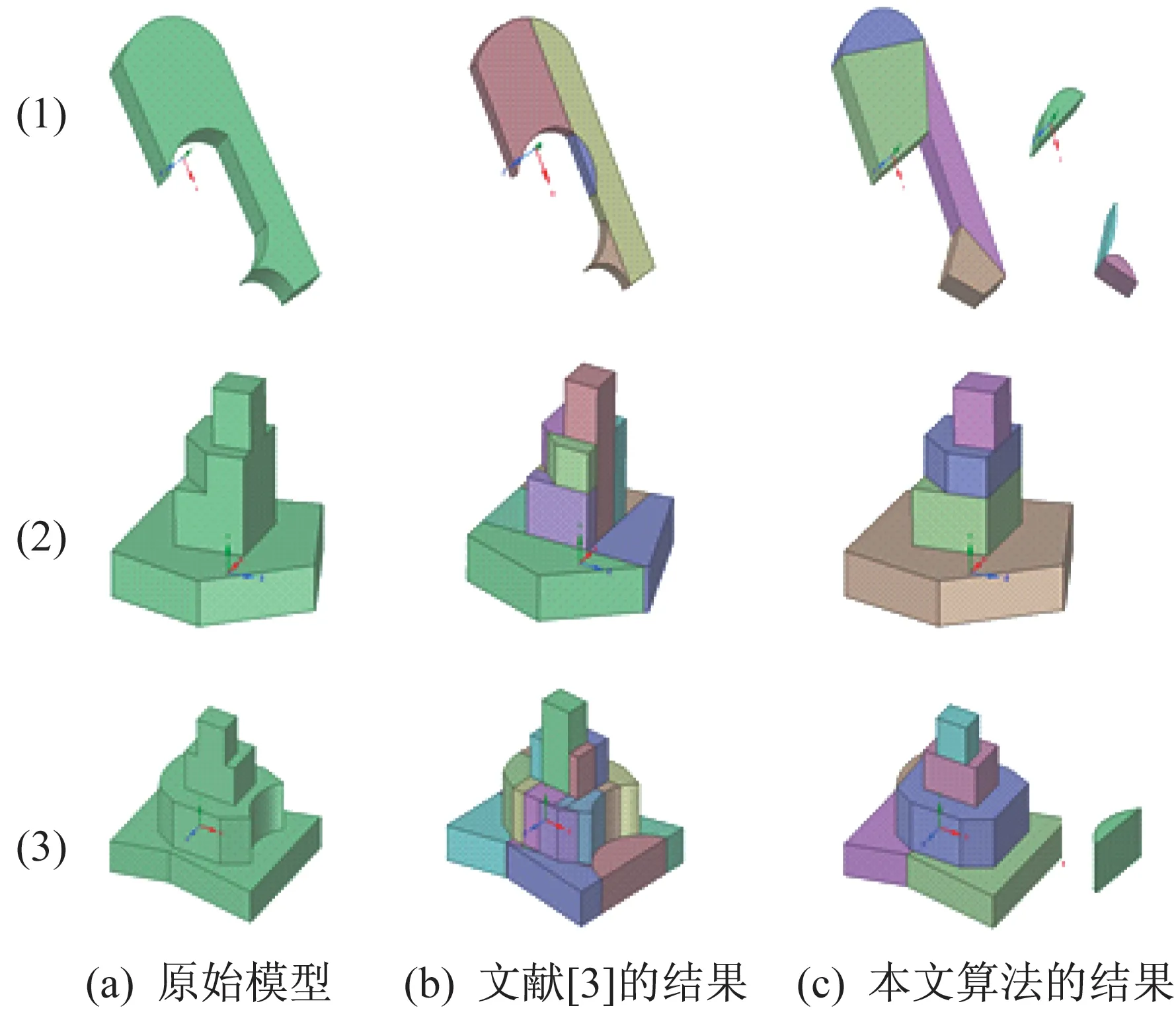
圖14 測試分解結果展示Fig.14 Display of test results

用具有代表性的AP1000 裂變堆堆芯模型進行測試（如圖3 所示）。AP1000 是我國引進的由美國西屋公司設計的第3 代先進反應堆，其包含665 個B-Rep 模型，所有模型均為拉伸體，采用本文算法后，B-Rep→CSG 轉換時間由130 079 ms 降至7 781 ms，速度提升了39%。但由于此案例中的BRep 對象均較簡單，尚難體現本文算法的優勢。

本文算法的主要優勢是降低了對布爾運算的依賴，提高了算法的穩定性。但因布爾運算失敗具有偶然性，難以準確復現，本文尚無法用實驗證明此優勢。

4 結 語

半空間分割法是應用最廣泛的B-Rep→CSG轉換算法之一，其核心是將B-Rep 模型分解為一組簡單模型，在實現過程中，依賴三維造型引擎的布爾運算，但因造型引擎的布爾運算存在失敗概率，從而影響B-Rep→CSG 轉換算法的穩定性，尤其對批量轉換軟件，不穩定性會嚴重影響軟件的可用性和友好性。本文利用拉伸特征，將三維B-Rep 模型的B-Rep→CSG 轉換問題轉變為二維圖形的B-Rep→CSG 轉換問題，從而降低對布爾運算的依賴，提高轉換算法的穩定性，同時提高了轉換算法的速度。

提出了基于拉伸邊的拉伸特征識別方法，通過觀察和總結，得到拉伸邊的相互平行性、首尾相連性、方向相反性、唯一連接性4 個特征，在此基礎上提出基于平行邊連接圖的拉伸特征識別算法。在拉伸特征識別算法的基礎上，結合基于環收縮的模型分割算法和基于頂點可見的多邊形分解算法，實現了三維模型的B-Rep→CSG 轉換，并在cosVMPT軟件中進行了測試，測試結果驗證了算法的有效性和優越性。

本文的拉伸特征識別算法依賴相互平行性、首尾相連性、方向相反性、唯一連接性等實踐經驗，沒能對算法的完備性進行嚴格證明，有待今后進一步研究；另外，本文討論的是拉伸特征，在實踐中存在大量旋轉特征，將旋轉特征的三維問題轉換為二維問題，也有待下一步研究，以進一步擴大本文算法的應用領域。