帶2 個形狀參數的多項式可展曲面造型

王海波，楊當福，佘衛勤，劉圣軍，劉新儒*，陳月安，白燕羽

（1.中南大學工程建模與科學計算研究所，湖南長沙 410083；2.中國航發南方工業有限公司，湖南 株洲 12000）

0 引 言

隨著計算機技術的發展，計算機輔助幾何設計在機械、航空、建筑等領域得到了廣泛應用，曲線曲面表示方法作為計算機輔助幾何設計中的重要方法［1］，廣受學者關注。在曲線曲面表示方法中，基函數的構造尤為重要。

傳統的Bézier 基函數、B 樣條基函數雖然具有很多優良性質，但一旦曲線曲面的控制頂點確定，其形狀也隨之確定，而在實際應用中，往往需要對曲線曲面的形狀進行微調。文獻［2］將權因子引入有理Bézier 曲線，文獻［3-4］在線性無關的三角函數生成空間中，構造了帶參數的三角Bézier 基函數，通過調節權因子或參數達到調節曲線形狀的目的。與有理基函數、三角Bézier 基函數相比，多項式基函數具有易于求導、計算簡便等優點。文獻［5-8］構造了一系列帶形狀參數的擴展Bézier 基函數，增加了曲線曲面的自由度，便于調節形狀。此外，求插值于給定數據點的Bézier 曲線或B 樣條曲線通常通過求解線性方程組實現，此方法雖然可滿足曲線光順、保凸等要求，但求解線性方程組的工作量較大。文獻［9-14］分別基于不同的基函數（包括（有理）多項式插值樣條基函數、（有理）三角插值樣條基函數）構造了保形插值曲線，并推導了形狀參數和局部參數的約束條件。另外，通過調節參數大小，可獲得光順性更好的插值曲線。

可展曲面因其獨特的性質在工業設計與制造中應用廣泛。現有的可展曲面設計方法主要有2 種：（1）將可展曲面看作直紋面的特殊情況，予張量積直紋面以一定的約束，求解特征方程組［15-17］；（2）利用點面幾何的對偶性設計可展曲面［18］。第1 種方法所形成的特征方程組通常呈非線性，求解較困難；第2 種方法在調節可展曲面的形狀上有一定欠缺。文獻［19-23］在第2 種方法基礎上，構造了一系列帶形狀參數的可展曲面，一定程度上彌補了第2 種方法的不足。

本文提出一種新的帶2 個形狀參數的四次多項式基函數。該基函數具有較好的形狀調節能力和良好的性質。特別地，當2 個形狀參數都等于0 時，該基函數就退化為三次伯恩斯坦基函數。利用此基函數，構造了G1連續插值樣條，并討論了樣條曲線的保形性。另外，基于對偶性原理，設計了可展曲面，討論了構造G0、G1、G2和G3連續曲面時參數的選取條件。最后，用具體實例進行了說明。

1 帶2 個形狀參數的多項式基函數

定義1對任意的t∈[0，1]，λ1，λ2∈[0，1]，

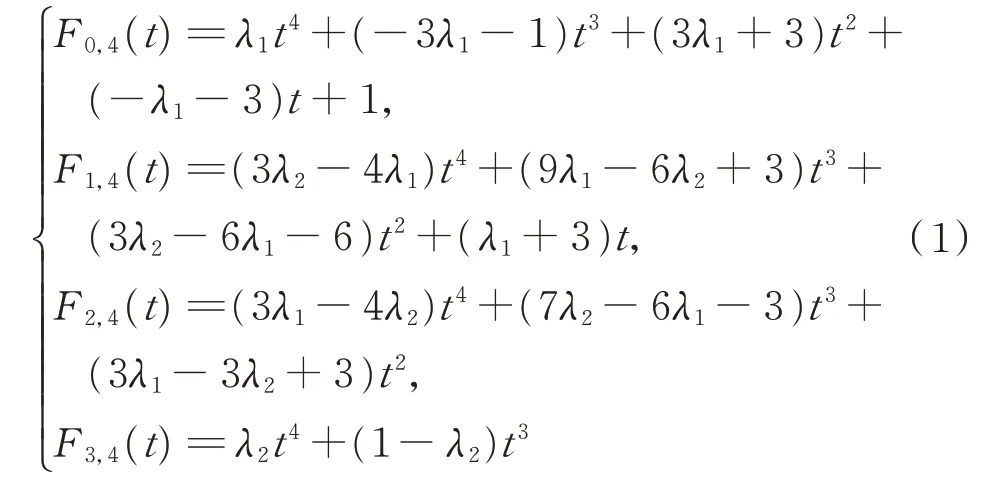
為帶2 個形狀參數λ1，λ2的四次多項式基函數。

1.1 基函數的性質

（ⅰ）退化性：當λ1=λ2=0 時，式（1）退化為三次伯恩斯坦基函數。

（ⅱ）非負性：對任意的λ1，λ2∈[0，1]，有Fi，4(t) ≥0，i=0，1，2，3。

證明將式（1）改寫為

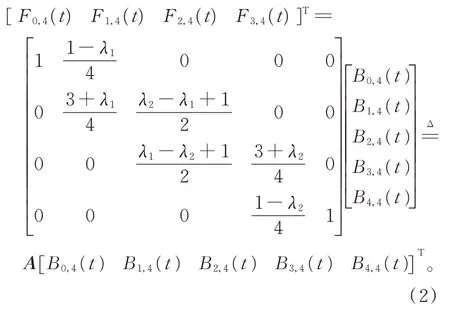
其 中，Bi，4(t)(i=0，1，…，4)為四次伯恩斯坦基函數，當λ1，λ2∈[0，1]時，矩陣A的元素均非負，而四次伯恩斯坦基函數也非負，故對任意的λ1，λ2∈[0，1]，均有Fi，4(t) ≥0，i=0，1，2，3。

（ⅲ）歸一性：對任意的λ1，λ2∈[0，1]，有

（ⅳ）端點性：對任意的λ1，λ2∈[0，1]，有

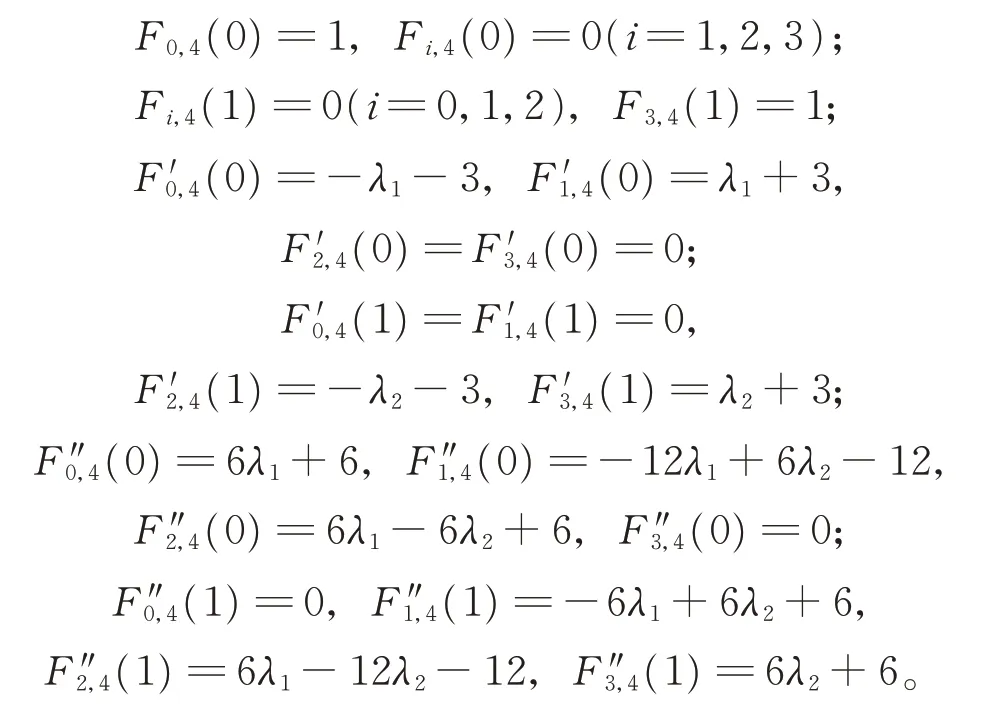
（ⅴ）對稱性：當λ1=λ2時，有

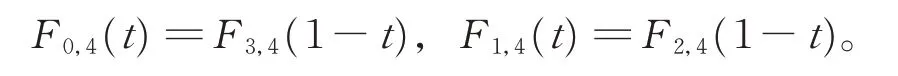
（ⅵ）線性無關性：對任意的λ1，λ2∈[0，1]，Fi，4(t) (i=0，1，2，3)線性無關。

1.2 逼近性質及形狀控制

定義 2給定 4 個控制頂點Pi∈Ru(u=2，3；i=0，1，2，3)，帶2 個形狀參數的曲線表達式為

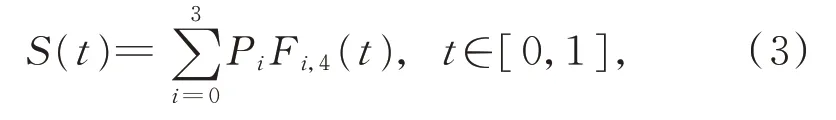
其 中，λ1，λ2∈[0，1]，Fi，4(t) (i=0，1，2，3)為 式（1）中定義的基函數。

對任意的λ1，λ2∈[0，1]，該曲線有以下性質：

（ⅰ）端點性

端點滿足：

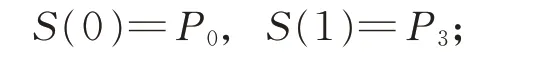
端點導數滿足：

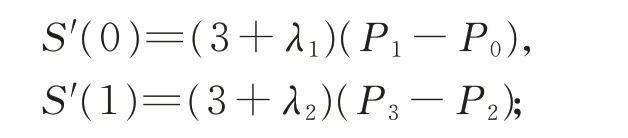
端點二階導數滿足：

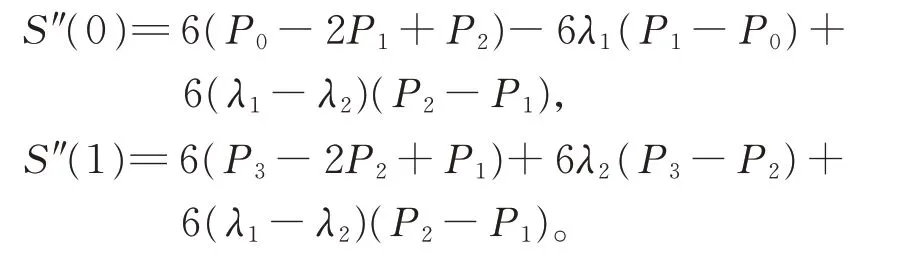
（ⅱ）對稱性

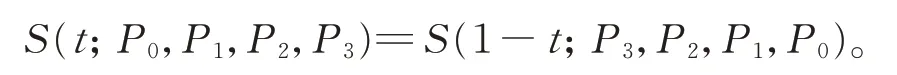
（ⅲ）凸包性

所生成的曲線始終位于Pi∈Ru(u=2，3，i=0，1，2，3)所構成的凸包內。

（ⅳ）變差減少性

除包含控制多邊形的整個平面外，任意平面與該曲線的交點數均不會超過該曲線與控制多邊形的交點數。

（ⅴ）平移與仿射不變性

該曲線滿足

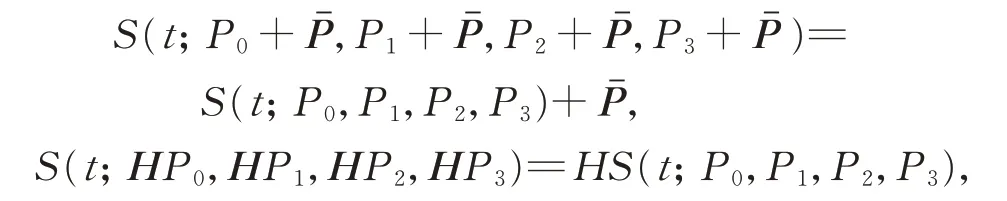
其 中，為Ru(u=2，3)中的任意向量，H為任意u×u(u=2，3)階矩陣。

（ⅵ）形狀可調性

該曲線的2 個形狀參數λ1，λ2∈[0，1]，增加了曲線的自由度。

形狀調節可視化效果如圖1 所示，其中，黑實線表示控制多邊形，圖1（a）中，λ2=0，紅、綠、藍、黃、黑、青 虛 線 分 別 表 示λ1=0，0.2，0.4，0.6，0.8，1.0；（b）中，λ1=0，紅、綠、藍、黃、黑、青虛線分別表示λ2=0，0.2，0.4，0.6，0.8，1.0；（c）中，λ1+λ2=1，紅、綠、藍、黃、黑、青 虛 線 分 別 表 示λ1=0，0.2，0.4，0.6，0.8，1.0；（d）中，λ1=λ2，紅、綠、藍、黃、黑、青 虛線分別表示λ1=λ2=0，0.2，0.4，0.6，0.8，1.0。 由圖 1 可知，對于固定的t（t∈[0，1]），當只增大λ1時，曲線向控制頂點P2偏移；當只增大λ2時，曲線向控制頂點P1偏移；當增大λ1、減小λ2時，曲線向控制頂點P2偏移；當同時增大λ1和λ2時，曲線向控制多邊形靠近。

1.3 保正插值及條件

定義3給定一組數據點(xi，yi)(i=1，2，…，n)，其中，x1＜x2＜…＜xn，四次插值樣條為

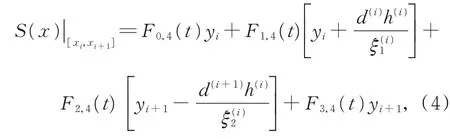
其中，Fj，4(t)(j=0，1，2，3)為式（1）定義的基函數，為插值曲線在xi處的導數值，基于文獻［11］中的算術平均方法即式（4）計算得到。記區間[xi，xi+1] (i=1，2，…，n?1)上 的 第i條 曲 線 段為s(i)(x)。

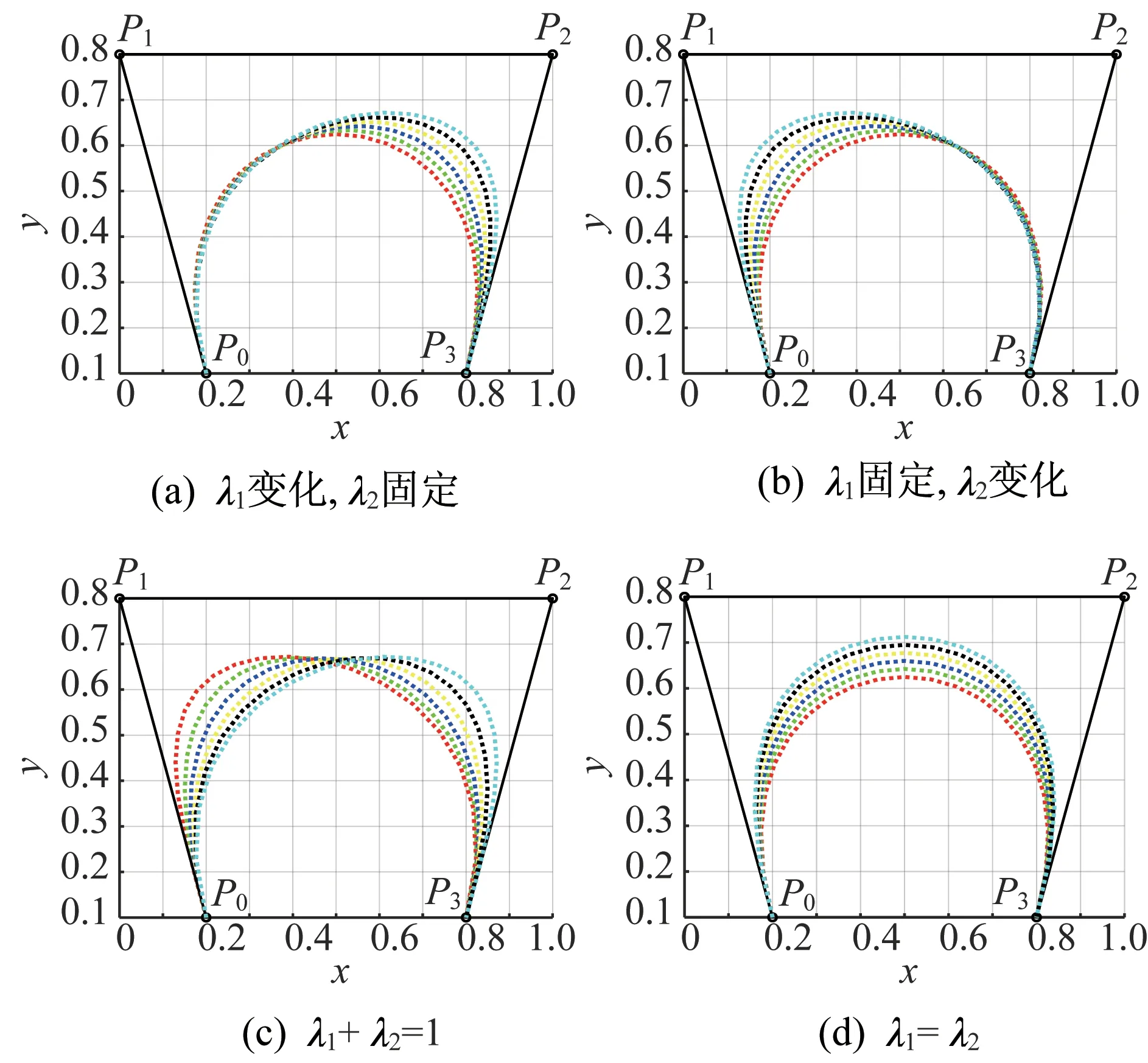
圖1 形狀參數對曲線的調節作用Fig.1 The adjustment effect of shape parameters on the curve

由基函數的端點性質和式（4）、式（5），有

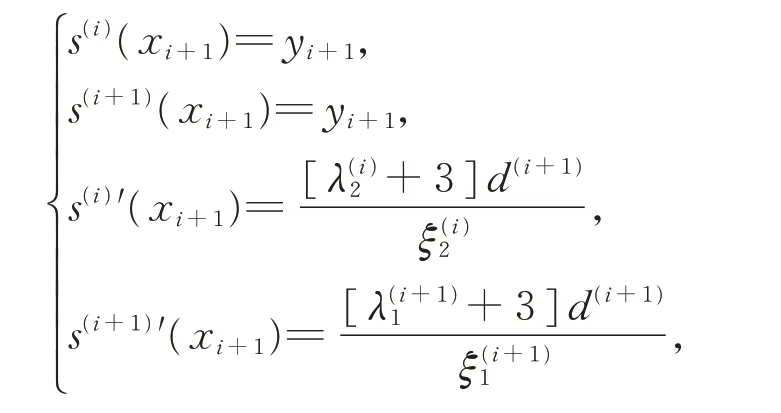
其中，i=1，2，…，n?1。則S(x)插值于所有給定的數據點，而且在相鄰曲線段的連接點處可達G1連續。

對于給定的數據點(xi，yi)(i=1，2，…，n)，若yi＞0(i=1，2，…，n)，使 得S(x)＞0，x∈[x1，xn]，則稱插值曲線具有保正性。

不失一般性，考慮區間[xi，xi+1]上的曲線段s(i)(x)(i=1，2，…，n?1)。利用式（2），將式（4）改寫為

由yi＞0(i=1，2，…，n)及式（6），可得使s(i)(x)＞0成立的充分條件為

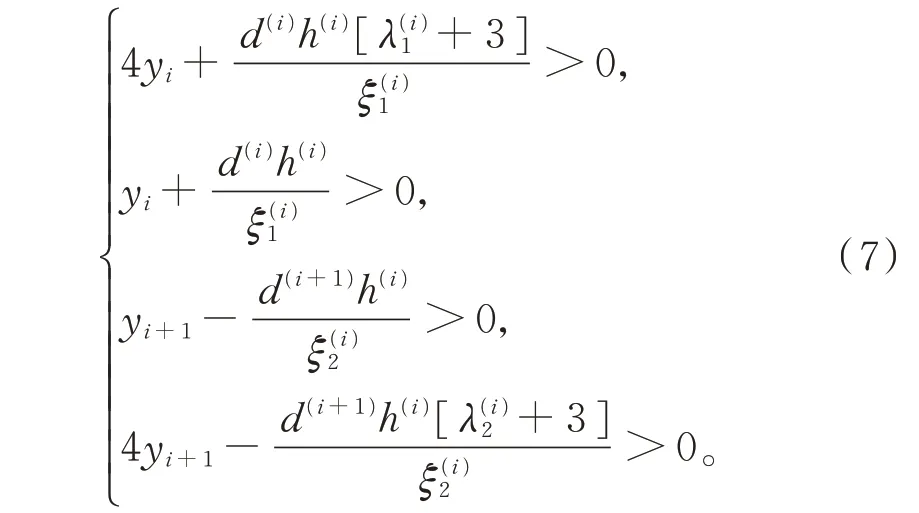
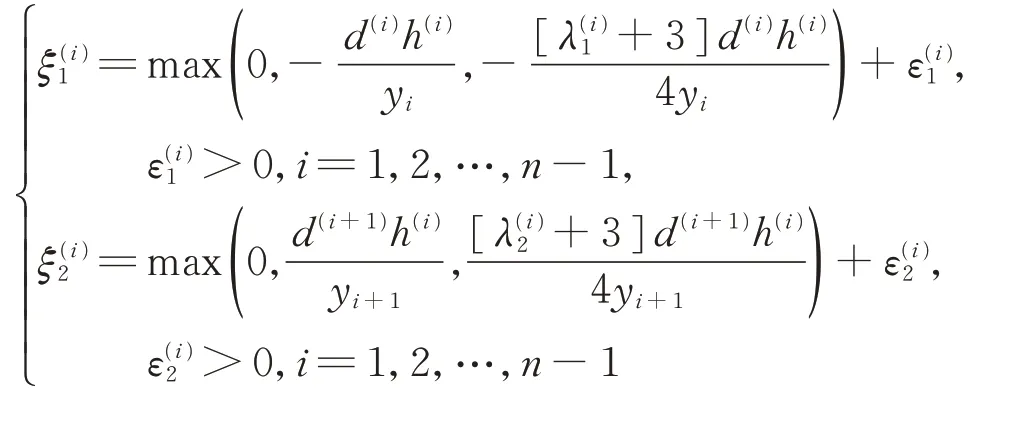
時，有S(x)＞0，x∈[x1，xn]。 通過調節可使曲線更加光順。

1.4 保單調插值及條件

式（4）所定義的插值樣條不僅具有保正性，而且在一定條件下還具有保單調性。下面分析插值樣條的保單調性及其條件。

對于給定的單調數據點(xi，yi)(i=1，2，…，n)，即yi+1≥yi或yi+1≤yi(i= 1，2，…，n?1)，x∈[x1，xn]，使得S′(x)≥0，則稱插值曲線具有保單調性。本文只考慮數據點單調遞增的情況，數據點單調遞減的情況類似可證。

不失一般性，考慮在區間[xi，xi+1]上的曲線段s(i)(x)(i=1，2，…，n?1)，對 式（6）求導，經整理可得

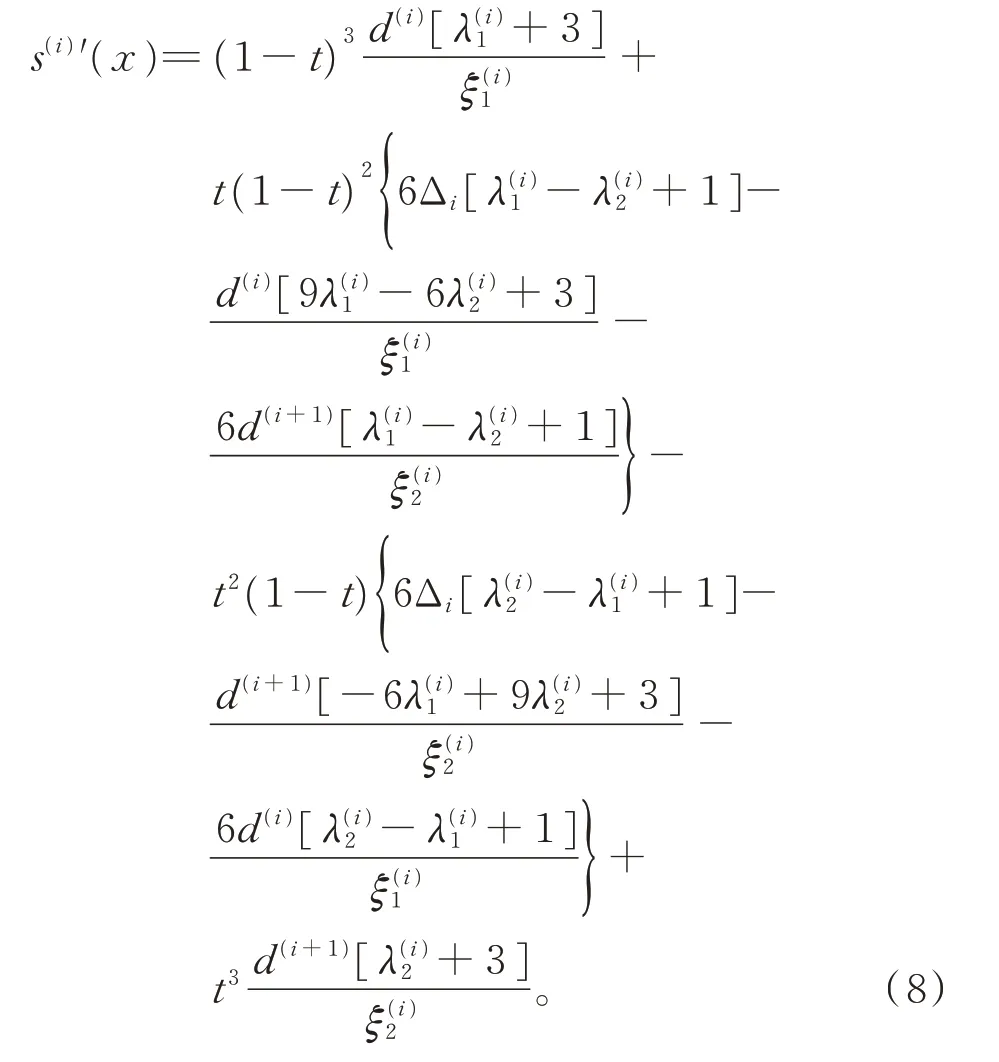
當yi+1≥yi(i=1，2，…，n?1)，即Δi≥0 時，由 式（5）可 知，d(i)≥0，故由式（8），得到滿足S′(x)≥0(x∈[x1，xn])的充分條件為

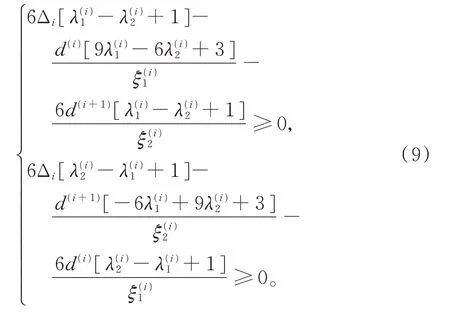
（ⅰ）當滿足Δi=0，時，有di=di+1=0，則對任意的均 有s(i)′(x)=0，并且在區間[xi，xi+1]上的曲線段s(i)(x)=yi=yi+1。

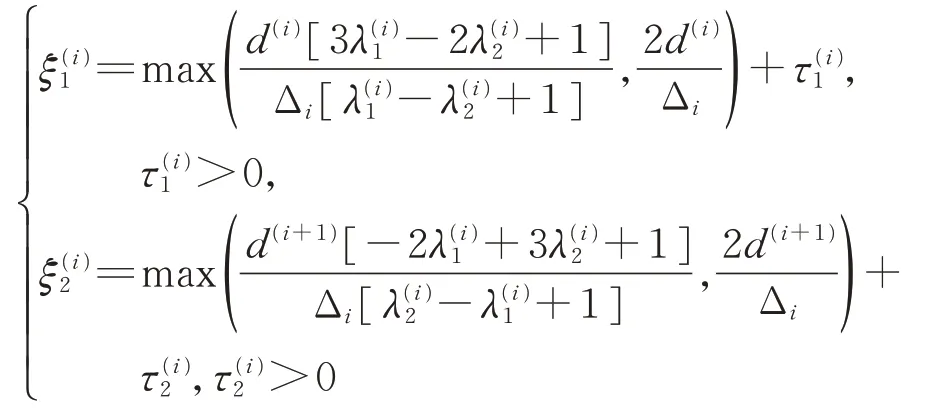
時，有S′(x)≥0(x∈[x1，xn])。

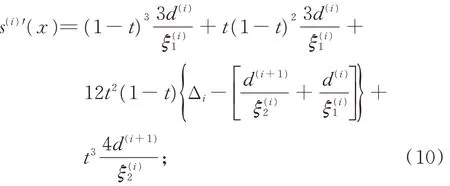
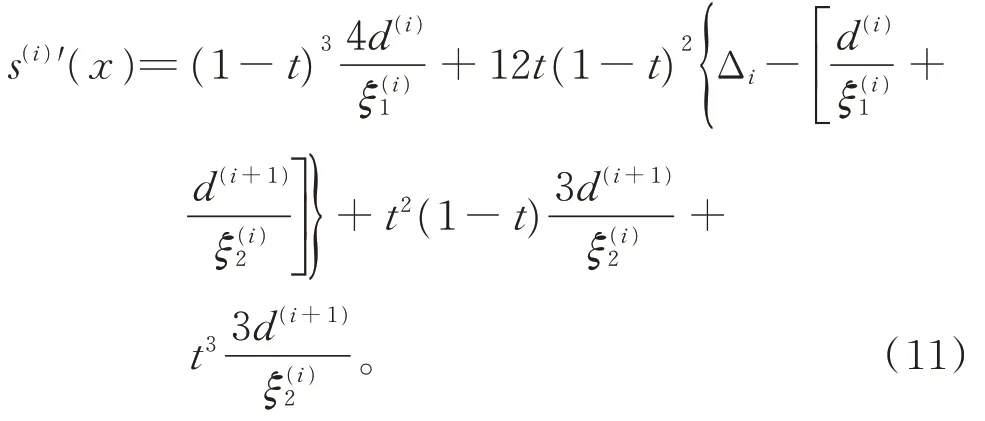
由式（10）和式（11）可知，當Δi＞0 時，取

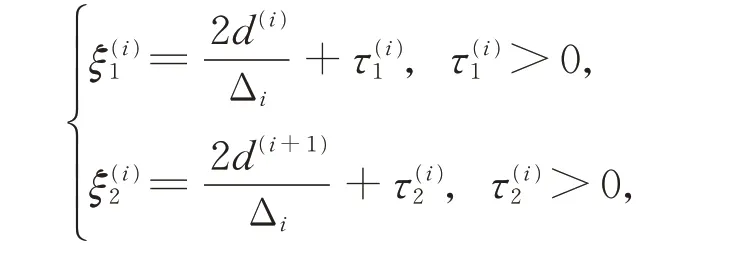
可得S′(x)≥0(x∈[x1，xn])。

2 可展曲面構造

由3D 射影空間中點與平面的對偶性，將式（3）中的控制頂點Pi(i=0，1，2，3)替代為控制平面Qi(i=0，1，2，3)，便可得到帶2 個形狀參數的單參數平面族

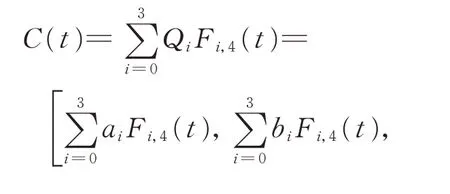
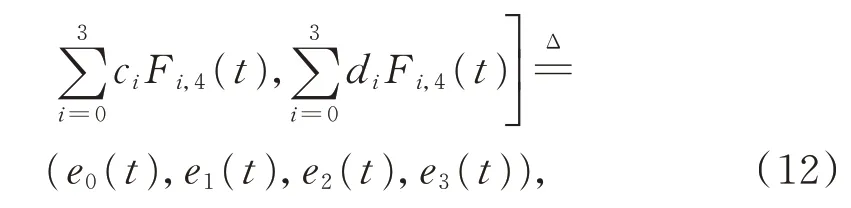
其 中，t∈[0，1]，Qi=(ai，bi，ci，di)，ai，bi，ci，di∈R(i=0，1，2，3)為控制平面，ai，bi，ci為控制平面上的點，di為(ai，bi，ci)到原點的距離。

2.1 包絡可展曲面構造

在式（12）定義的帶2 個形狀參數的單參數平面族中，2 個相鄰的平面相交于一條直線，且該直線位于包絡可展曲面上。式（12）中，對應于任意一個t值的平面可表示為向量形式：

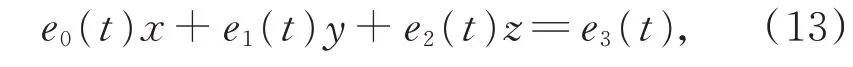
記為E(t)X=e3(t)，其中，

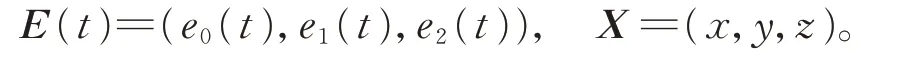
對式（13）求一階導數，得

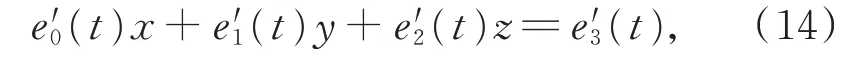
記為E′(t)X=e′3(t)，其中，

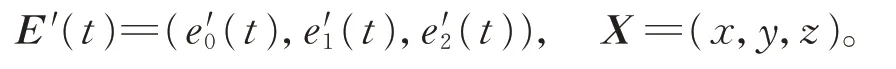
則式（13）和式（14）所形成的2 個平面的交線即曲面與t的母線，在可展曲面上，計算該交線L(t)=(u，v)，其中，u=E(t)×E′(t)為L(t)的法向量，v=e′(t)E(t)?e(t)E′(t)。設p(t)為直線上與t最接近原點的點，則p(t)=。因而L(t)的方程可用以下參數形式表示：

2.2 脊線可展曲面構造

在式（12）定義的帶2 個形狀參數的單參數平面族中，3 個相鄰平面的交點q(t)稱為t的特征點，這些特征點形成的曲線，即為脊線。

對式（13）求二階導數，得

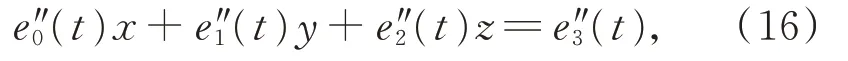
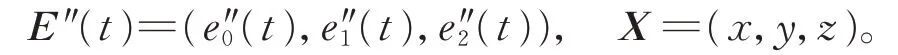
則q(t)可表示為

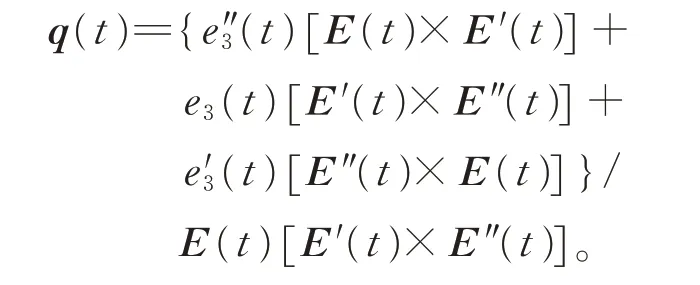
因此，可展曲面的參數表達式為

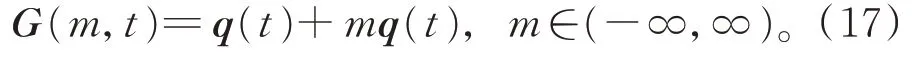
3 可展曲面的拼接連續性分析

假設待拼接的兩可展曲面為

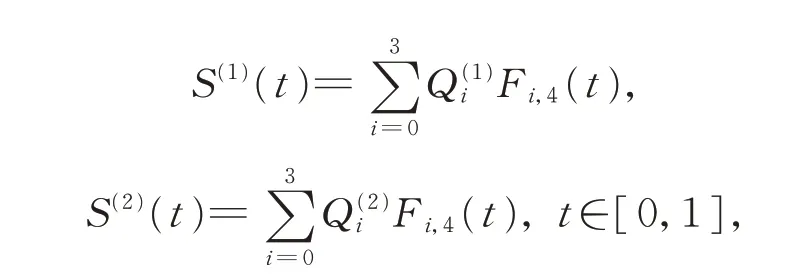
3.1 可展曲面的G0 連續拼接

若S(2)(0)=S(1)(1)，則稱兩曲面G0連續。可得滿足G0連續拼接的條件為

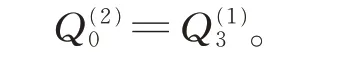
3.2 可展曲面的G1 連續拼接

其中，β1＞0 為常數，則稱兩曲面G1連續。可得滿足G1連續拼接的條件為

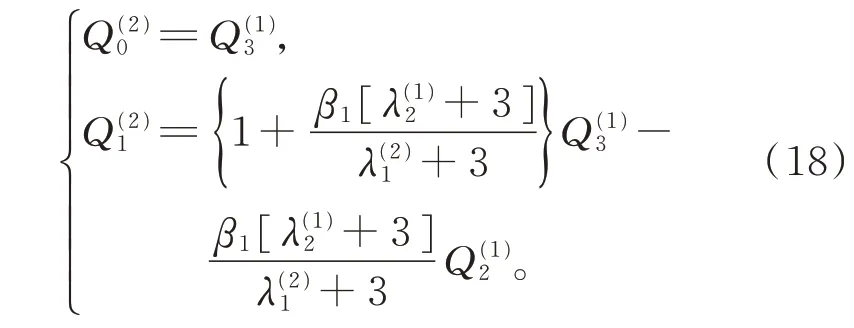
3.3 可展曲面的Farin-Boehm G2 連續拼接

若

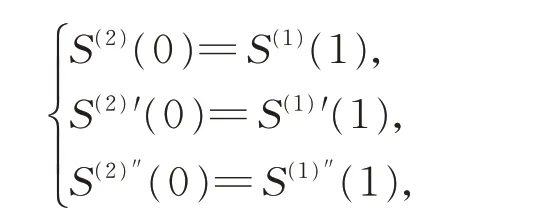
則稱兩曲面Farin-BoehmG2連續。當1≠0 時，可得滿足Farin-BoehmG2連續拼接的條件為

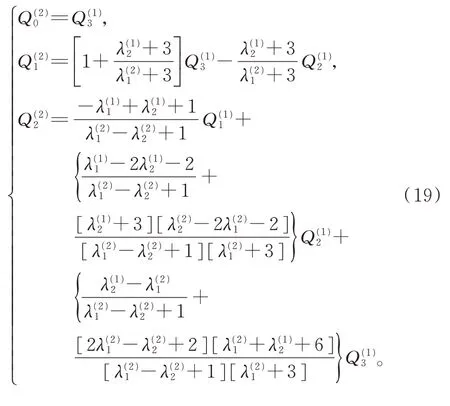
3.4 可展曲面的G2 beta 連續拼接

其中，β1＞0，β2為常數，則稱兩曲面G2beta連續。當時，滿足G2beta連續拼接的條件為

3.5 可展曲面的G3 beta 連續拼接

若

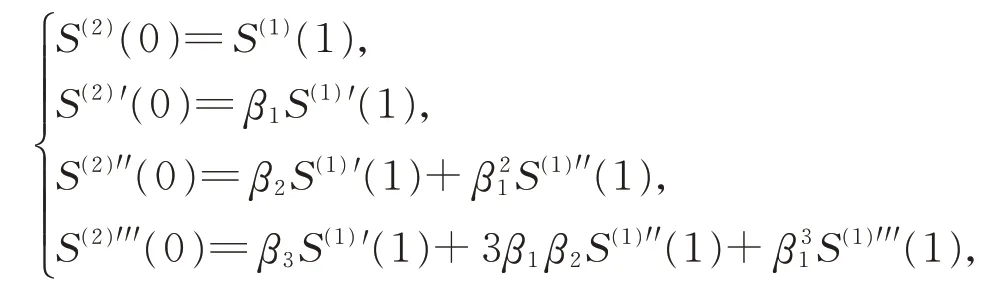
其中，β1＞0，β2，β3為常數，則稱兩曲面G3beta 連續。當時，滿足G3beta 連續拼接的條件如式（21）所示。

4 實例分析

4.1 形狀參數

為更好地說明形狀參數的調節作用，圖2 給出了4 類曲線的幾何造型實例。在圖2（a）梨子、（b）蝴蝶中，實線、虛線、雙劃線所對應的參數值分別為λ1=λ2=0，0.5，1，隨著λ1，λ2的增大，梨子、蝴蝶逐漸變大。在圖2（c）花瓣、（d）楓葉中，實線、虛線、雙劃線所對應的參數值分別為λ1=0，λ2=1；λ1=0.5，λ2=0.5；λ1=1，λ2=0，隨著λ1，λ2的變化，花瓣、楓葉的形狀發生了變化。

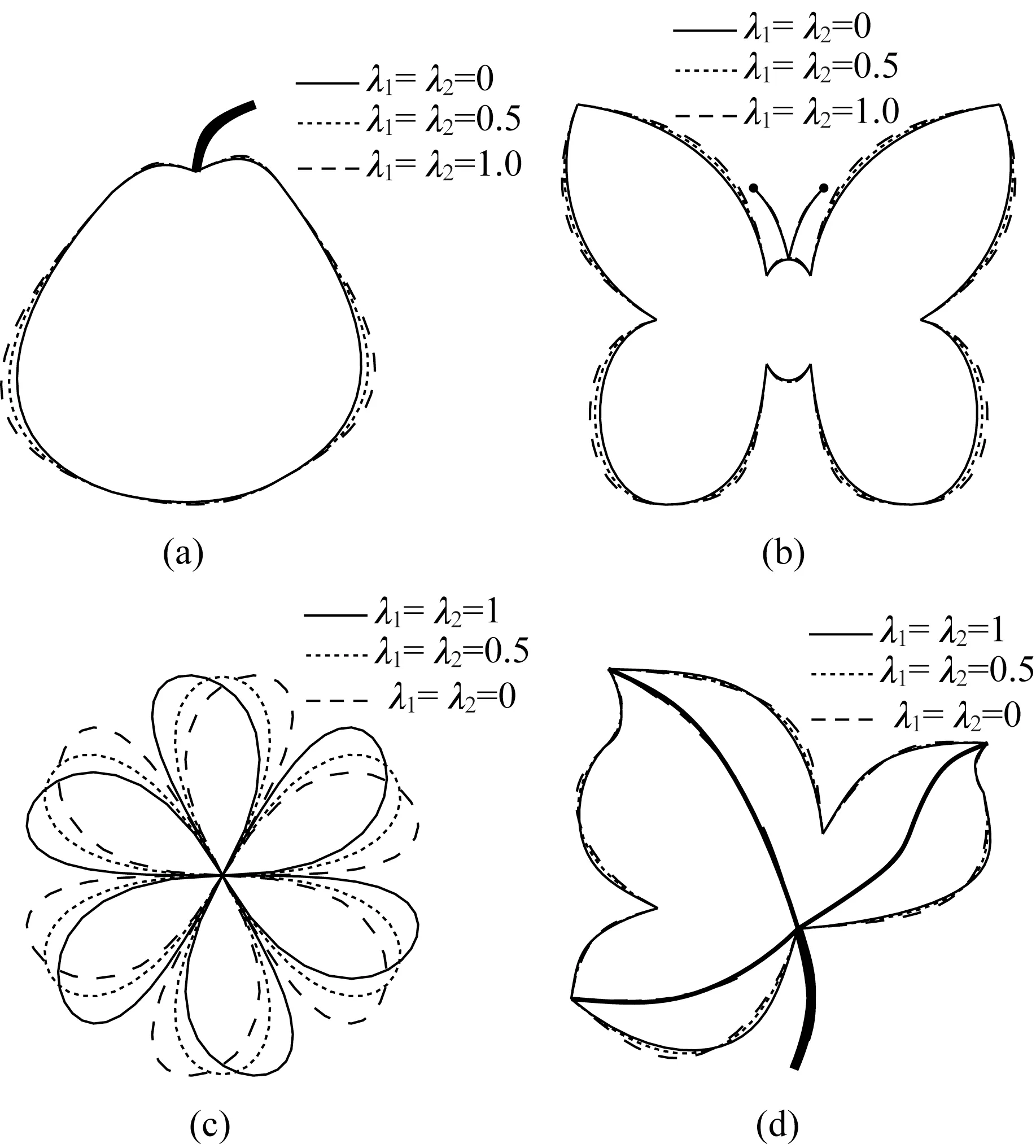
圖2 曲線圖形造型實例可視化Fig.2 Visualization of curve graphic modeling examples

4.2 插值樣條的保正性

表1 所示為文獻［12］中的正數據集。圖3 為保正插值曲線可視化圖，其中，圖3（a）中，參數=1(i=1，2，…，6)，ξ1=(3，15，1，1，20，10)，ξ2=(3，2，1，1，4，5)，（b）中，參數λ1=(0，0.9，0.5，0.2，0.8，1.0)，λ2=(0，0.6，0.1，0.5，0.5，1.0)，ε1=(3，1，3，3，3，8)，ε2=(4，0，2，5，5，3)。表2 為文獻［14］中的正數據集。圖3（c）中，參數=1(i=1，2，…，7)，ξ1=(3，1，1，1，1，1，1)，ξ2= (3，1，1，1，1，4，1)，（d）中，參數λ1=(0，1.0，0.5，0.2，0.8，1.0，0.5)，ε1=(3，3.5，3，3，3，1，8)，λ2= (0，1.0，0.1，0.5，0.5，1.0，0.8)，ε2=(4，3，2，5，5，3，2）。（a）和（c）中的參數是隨機選取的，曲線不保正。（b）和（d）中的參數滿足式（7），曲線是保正的。

表1 文獻［12］中的正數據集Table 1 Positive dataset in paper［12］

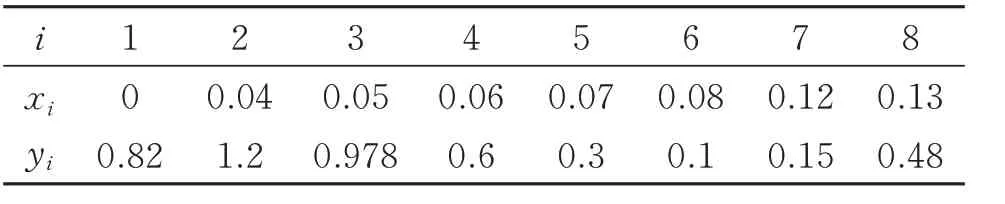
表2 文獻［14］中的正數據集Table 2 Positive dataset in paper［14］

4.3 插值樣條的保單調性

表3 為文獻［12］中的單調遞增數據集。圖4 為單調遞增插值曲線可視化圖，其中，圖4（a）中，參數=1(i=1，2，3)，ξ2=(1，3，1)，（b）中，參數λ1= (1，1，1)，λ2= (0.1，1，1)，τ1= (1，1，5)，τ2=(5，1，1)。表4 為文獻［14］中的單調遞增數據集。圖4（c）中，參數=1(i=1，2，…，10)，ξ2=(1，3，1，1，1，1，1，1，1，1)，（d）中，參數λ1=(1，1，1，1，1，1，1，1，0.2，1)，τ1=(1，1，1，1，1，1，1，1，12，1)，λ2=1(1，2，…，10)，τ2=(1，1，1，1，1，1，1，1，5，1)。（a）和（c）中的參數是隨機選取的，為非單調曲線。（b）和（d）中的參數滿足式（9），為單調曲線。

圖4 單調遞增插值曲線可視化Fig.4 Visualization of monotonically increasing interpolation curve

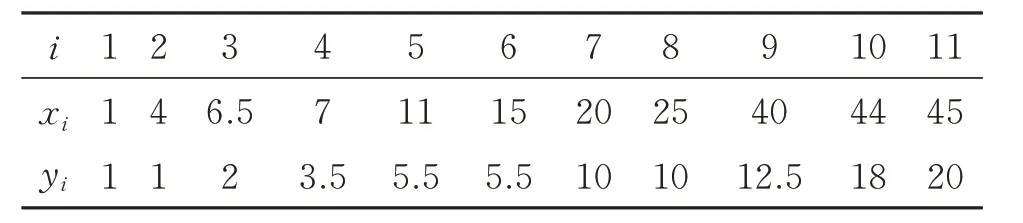
表4 文獻［14］中的單調數據集Table 4 Monotonically increasing dataset in paper［14］

4.4 包絡可展曲面

由文獻［20］中4 個控制平面

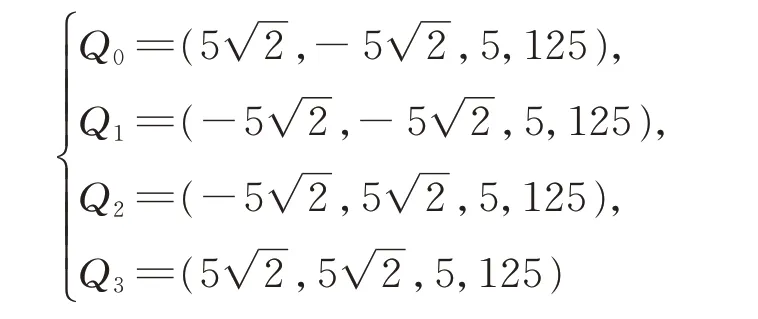
所設計的包絡可展曲面如圖5～圖7 所示。由圖5可知，當λ2不變時，隨λ1的增大，曲面的起始邊(t=0)不斷變長，終止邊(t=1)的卷曲程度不斷增加。由圖6 可知，當λ1不變時，隨λ2的增大，曲面的起始邊(t=0)的卷曲程度不斷增加，終止邊(t=1)不斷變長。由圖7 可知，當λ1和λ2同時增大時，曲面的起始邊和終止邊均不斷變長，彎曲程度有所增加。

圖5 λ1 對包絡可展曲面的影響可視化Fig.5 Visualization of the influence of λ1 on the enveloping developable surface

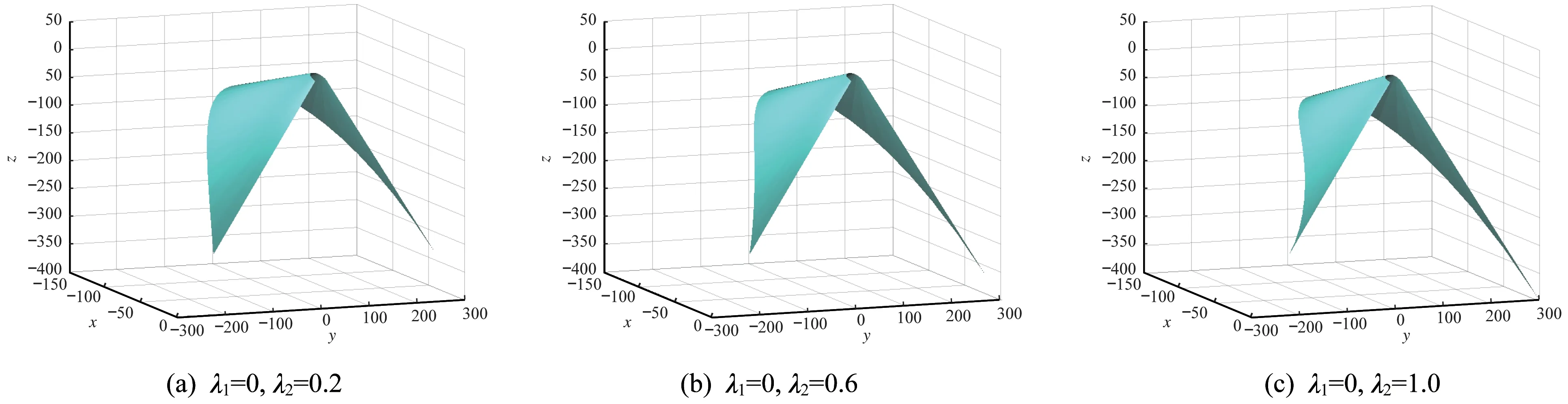
圖6 λ2 對包絡可展曲面的影響可視化Fig.6 Visualization of the influence of λ2 on the enveloping developable surface

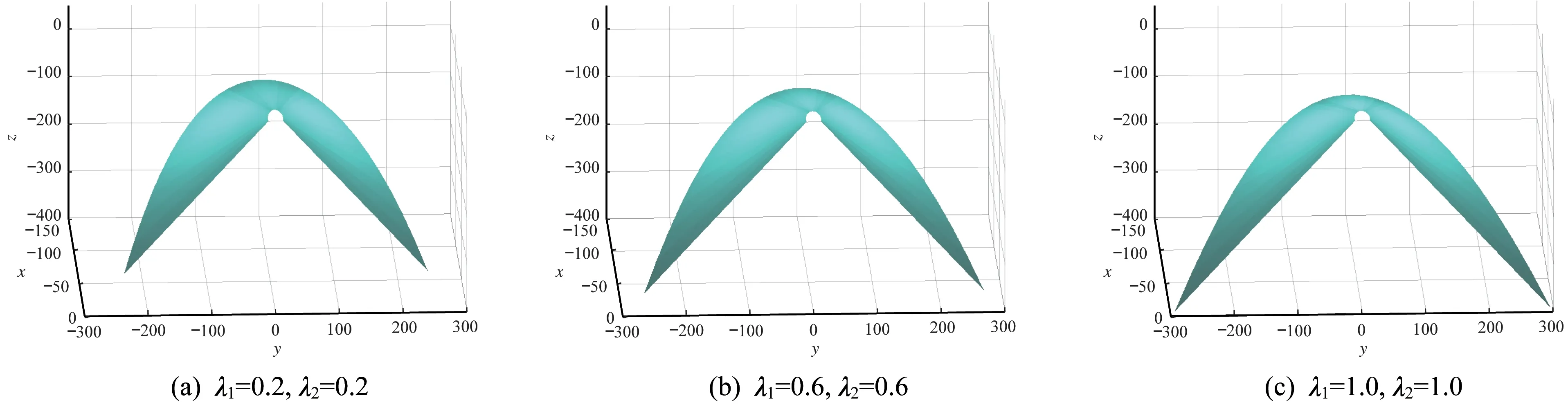
圖7 λ1，λ2 對包絡可展曲面的影響可視化Fig.7 Visualization of the influence of λ1，λ2 on the enveloping developable surface

4.5 脊線可展曲面

由文獻［20］中4 個控制平面

所設計的脊線可展曲面如圖8～圖10 所示。由圖8可知，當λ2不變時，隨λ1的增大，曲面的起始邊(t=0)不斷變短，終止邊(t=1)的卷曲程度不斷增大。由圖9 可知，當λ1不變時，隨λ2的增大，曲面的起始邊(t=0)的卷曲程度不斷增加，終止邊(t=1)不斷變短。由圖10 可知，當λ1和λ2同時增大時，曲面的起始邊和終止邊都不斷變長，彎曲程度有所增加。

4.6 可展曲面的連續性拼接

由文獻［20］中4 個控制平面

作為以下連續性例子的第1 個包絡可展曲面的控制平面。由式（18）得到第2 個可展曲面的前2 個控制平面，任給后2 個控制平面即可達到G1連續。取β1=1，=0，設第2 個可展曲面的控制平面為

由式（19）、式（20）可得，第2 個可展曲面的前3個控制平面，任給最后一個控制平面，即達到Farin-BoehmG2連 續、G2beta 連續，由式（21）可得，第2 個可展曲面的所有控制平面達到G3beta 連續。連續性條件的參數設置、第2 個可展曲面的控制平面設置如表5 所示，拼接可展曲面可視化及相應的拼接曲面連續性高光帶渲染結果如圖12 所示，其中天藍色曲面為第1 個可展曲面，米黃色曲面為第2 個可展曲面，紫紅色為高光帶。

5 結論及展望

圖8 λ1 對脊線可展曲面的影響可視化Fig.8 Visualization of the influence of λ1 on the spine curve developable surface

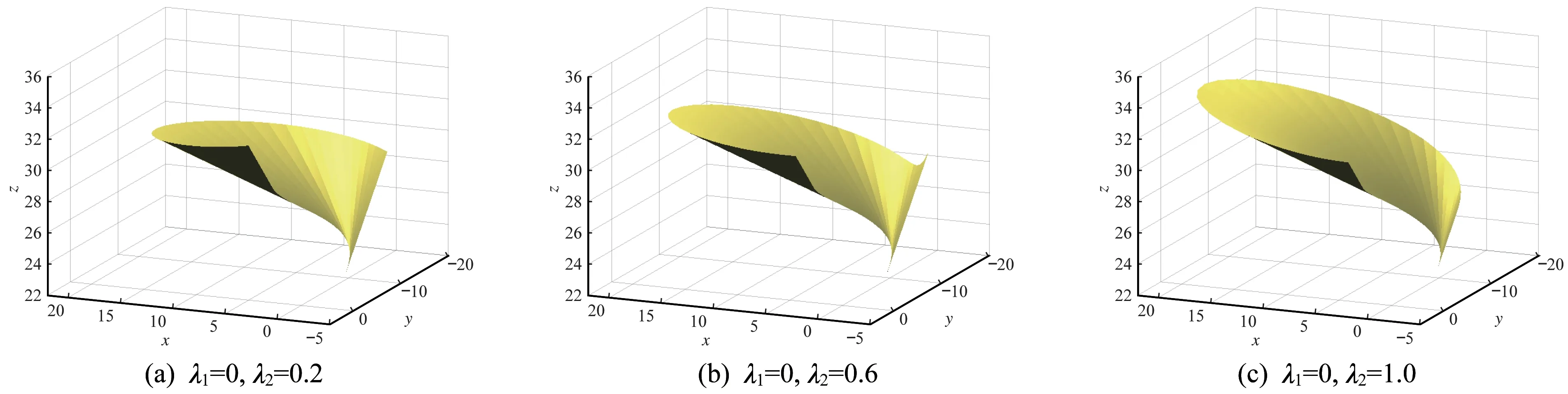
圖9 λ2 對脊線可展曲面的影響可視化Fig.9 Visualization of the influence of λ2 on the spine curve developable surface

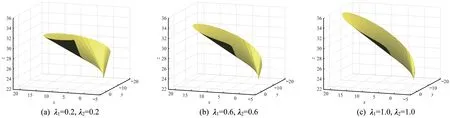
圖10 λ1，λ2 對脊線可展曲面的影響可視化Fig.10 Visualization of the influence of λ1，λ2 on the spine curve developable surface

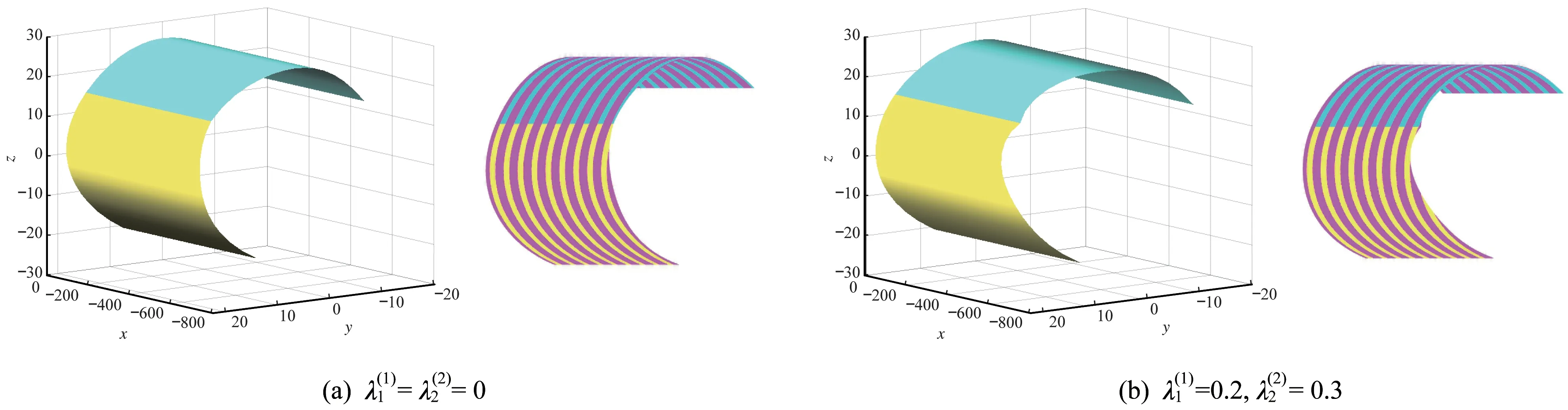
圖11 不同參數對拼接G1 連續可展曲面的影響可視化及拼接曲面連續性高光帶渲染結果Fig.11 Visualization of the effects of different parameters on the blending G1 continuous developable surfaces and rendering results of continuum highlight bands for blending surfaces

構造了帶2 個形狀參數的四次多項式基函數，是對三次伯恩斯坦基函數的擴展，具有退化性、非負性、歸一性、端點性、對稱性、線性無關性等性質。當該基函數用于構造曲線時，同樣具有端點性、對稱性、凸包性、變差減少性、平移與仿射不變性、形狀可調性等性質，可在不改變曲線控制頂點的前提下，通過改變形狀參數調節曲線形狀。在此基礎上，基于該基函數設計了4 次插值樣條，該插值樣條自動滿足G1連續。并討論了當形狀參數及局部參數滿足一定條件時，該插值樣條具有保正性和保單調性。此外，將該基函數用于構造可展曲面，利用對偶性理論設計脊線可展曲面和包絡可展曲面，并討論了包括G0連續、G1連續、Farin-BoehmG2連續、G2beta連續、G3beta 連續的可展曲面的連續性條件。最后通過具體實例進行了驗證分析。

表5 連續性條件的參數及第2 個可展曲面的控制平面設置Table 5 Parameter setting，control planes setting of the second developable surface of continuity condition

圖12 拼接可展曲面可視化及拼接曲面連續性高光帶渲染結果Fig.12 Visualization of the blending developable surfaces and rendering results of continuum highlight bands for blending surfaces

在設計可展曲面過程中，筆者發現控制平面的構造比較困難，其幾何意義不夠明確。如果能進一步探明可展曲面與其控制平面之間的幾何關系，探尋控制平面的構造規律，將極大擴展可展曲面的應用范圍。所有這些有待進一步研究。