基于東方螻蛄爪趾的仿生旋耕刀設計與試驗

肖茂華 汪開鑫 楊 望 王偉臣 江 豐

(1.南京農業大學工學院， 南京 210031; 2.廣西大學機械工程學院， 南寧 530004)

0 引言

旋耕刀是一種基于銑切原理加工的土壤耕作機械[1-2]。其中，旋耕彎刀是旋耕機的主要部件[3-5]，其性能直接影響整個旋耕機的作業質量和能耗水平。為了提高旋耕機工作效率，旋耕刀幾何結構優化設計一直是國內外研究的重點。郝建軍等[6]設計了一種楔形減阻旋耕刀，田間試驗表明，在相同工況下，楔形減阻旋耕刀的平均扭矩較國標旋耕刀降低11.35%，平均功耗較國標旋耕刀降低9.29%，碎土率提高4%。GODWIN[7]在研究土壤耕具作業時，獲得不同寬窄齒的耕具在土壤切削過程中所受的水平阻力變化規律。

近些年，隨著仿生學在農業領域的應用，土壤耕具作業時阻力大、能耗高的問題得到了一定的緩解。楊玉婉等[8]研究了前肢手掌的多趾組合結構特征，設計了具有鼴鼠多趾結構特征的仿生旋耕刀，通過田間試驗對比表明，在不同前進速度和彎刀轉速情況下，旋耕機整機功耗平均降低了約20%左右。俞杰[9]以安哥拉兔爪趾為原型設計了仿生旋耕刀，通過試驗得出，與傳統旋耕刀相比其工作時降阻率達到了17.8%，最大扭矩也降低了44.9 N·m。東方螻蛄俗稱“土仙”，挖土能力極強，前足特化為釘耙狀，能夠在一夜之間挖掘出2 000～3 000 mm長的洞穴[10]。目前，已有研究學者將東方螻蛄前爪趾應用于深松鏟、觸土試件以及挖掘機仿生斗齒的設計中[11-13]。本文基于東方螻蛄前足爪趾輪廓曲線，設計具有仿生結構特征的旋耕刀，借助仿真軟件進行離散元仿真分析，然后進行室內土槽試驗驗證，分析國標旋耕刀與仿生旋耕刀扭矩、三向阻力的變化規律，以期為旋耕刀的減阻降耗提供借鑒。

1 仿生旋耕刀設計

1.1 前足爪趾輪廓曲線擬合

東方螻蛄(圖1a)的前足為釘耙狀，具有較強的挖土性能。東方螻蛄前足爪趾輪廓相對較為復雜，因此需要將爪趾輪廓分為上、下曲線(圖1b)。通過研究上、下爪趾輪廓曲線獲得東方螻蛄前足爪趾曲線的趨勢[14]。

通過逆向工程技術及軟件對東方螻蛄前足爪趾的結構進行采樣和數據處理[15]，將得到的爪趾輪廓曲線的點云數據代入到AutoCAD 2016中，獲取爪趾輪廓曲線的X與Y坐標值數據，最后，使用曲線擬合(Curve fitting)工具箱將二維坐標數據導入到Matlab 2018。基于最小二乘法擬合東方螻蛄4個爪趾輪廓曲線(圖2)，4個爪趾輪廓擬合方程均為高斯方程，方程系數如表1、2所示。

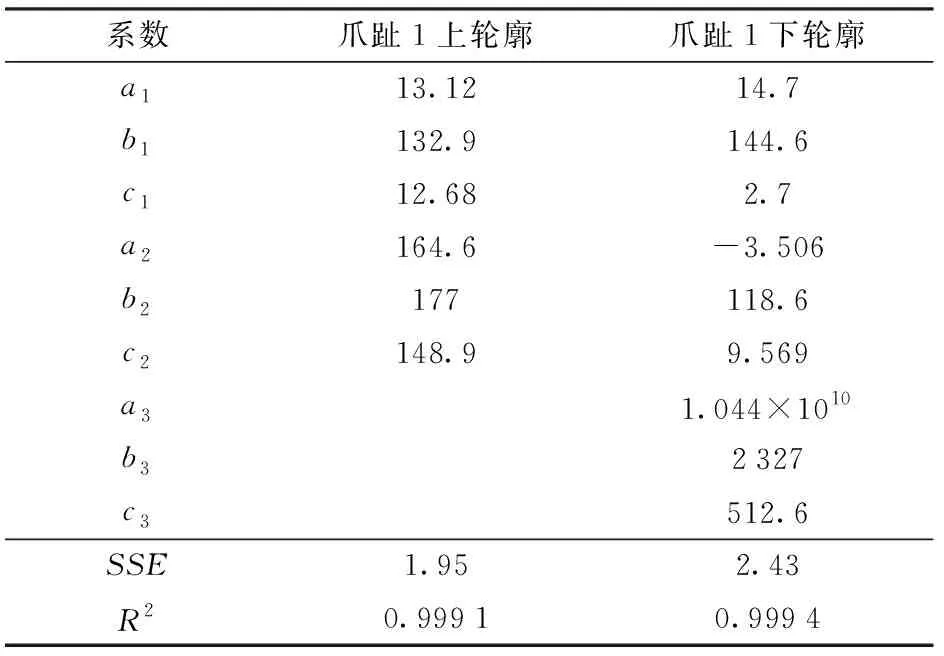
表1 東方螻蛄前足爪趾1擬合曲線方程系數Tab.1 Fitting curve equation coefficients of the first claw toe of Gryllotalpa orientalis Burmeister

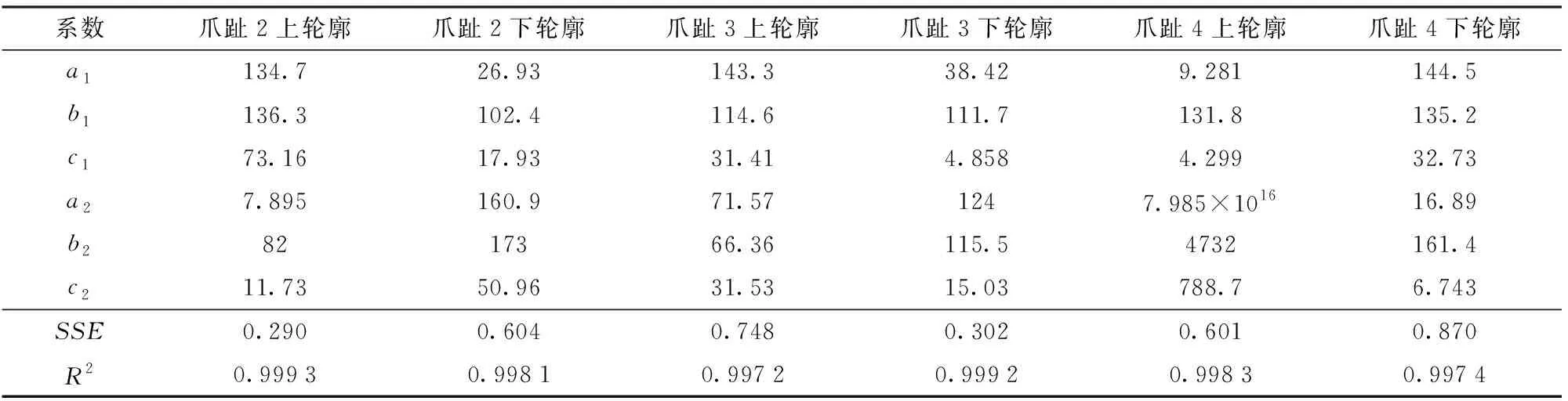
表2 東方螻蛄前足爪趾2、3、4擬合曲線方程系數Tab.2 Fitting curve equation coefficients of the second， third and fourth claws of Gryllotalpa orientalis Burmeister

爪趾1上輪廓高斯方程為

(1)

爪趾1下輪廓高斯方程為

(2)

爪趾2、3、4的上、下輪廓高斯方程為

(3)

1.2 設計原理與過程

目前，橫軸式旋耕機上采用的旋耕刀主要有彎形刀、直角刀以及鑿形刀3種類型[16]。本文從彎形刀入手，旋耕彎刀是由刀柄、包含側切刃的側切面、過渡刃的過渡面以及正切刃的正切面4部分組成[17]。通常情況下，旋耕刀主要的工作部位是正切刃與側切刃，而正切刃需承擔碎土、翻土以及切土的作用，因此為旋耕刀上最主要的耗能工作部件[18]。

東方螻蛄前足平行置于身體兩側并指向前方，但其爪趾向外翹起，這與旋耕刀的結構有一定的相似之處。東方螻蛄前足挖土運動軌跡近似為具有一定弧度的軌跡曲線[19]。而旋耕刀運動軌跡是由圓周運動和直線運動所組成的擺線運動[20]，兩者運動軌跡存在一定的差異。通過測量20只東方螻蛄前足與其4個爪趾長度、爪趾之間角度等信息，根據仿生設計中的比例法[21-22]，結合兩者運動軌跡與結構的異同性進行設計。由于東方螻蛄前足挖土過程中存在著伸展與向外擴張兩種運動，且擴張運動受力與旋耕刀側向阻力相似，因此在采用東方螻蛄爪趾輪廓曲線信息的同時，考慮了仿生齒形強度問題，將4個爪趾齒形的齒根長度L稍微加大，L1～L4分別為5.0、4.0、3.5、6.0 mm；減小兩齒間夾角α，α1～α4分別為21°、22°、33°、42°，具體如圖3所示。總體結構是依據國標旋耕刀的結構特征，將東方螻蛄前足的爪趾1、2、3、4的輪廓曲線依次排列于正切刃與回轉半徑的末端邊緣(圖4a)。

在國標刀座式旋耕刀毛坯的基礎上，仿生設計采用國標旋耕刀的回轉半徑R為245 mm，材質為65 Mn鋼。根據國家標準GB/T 5669—2008《旋耕機械 刀和刀座》[23]，刀身熱處理硬度為48～54 HRC；刀柄熱處理硬度為38～45 HRC，旋耕刀刀身部分金相組織為回火馬氏；刀柄部分為回火屈氏體，最后旋耕刀的表面無裂紋，實物如圖4b所示。

2 離散元仿真分析

采用EDEM 2018軟件對國標與仿生旋耕刀這2種刀片的耕作過程進行仿真試驗，對比2種旋耕刀所受的扭矩和三向阻力情況。

2.1 土壤顆粒接觸模型

采用Hertz-Mindlin with Bonding模型，此接觸模型在粘結土壤破碎的過程中具有很好的應用效果，能在土壤顆粒中產生一定的約束，這種土壤間的約束能對土壤產生切向和法向的運動阻力，直到顆粒彼此間的力達到破壞約束作用時，土壤顆粒間才會產生作用[24-26]。外界對土壤的法向粘結力Fn、法向力矩Mn、切向粘結力Fτ和切向力矩Mτ計算式為

δFn=-vnSnAδt

(4)

δFτ=-vτSτAδt

(5)

δMn=-ωnSnJδt

(6)

(7)

式中A——接觸區域面積,m2

Rb——粘結半徑,mm

J——截面積慣性矩,m4

Sn、Sτ——顆粒法向、切向粘結剛度,N/m3

vn、vτ——顆粒法向、切向速度,m/s

ωn、ωτ——顆粒法向、切向角速度,rad/s

δt——時間步長,s

當某一時刻外界作用力超過使土壤粘結的最大切向與法向作用力時，粘結會被破壞，土壤顆粒之間相互作用力將不會受到粘結作用的約束。定義條件為

(8)

(9)

式中δmax——法向臨界應力,Pa

τmax——切向臨界應力,Pa

2.2 土壤模型參數

EDEM離散元仿真基本原理是用球模擬土壤顆粒模型。目前，大多數研究者采用直徑小于10 mm的球體作為土壤模型[27-32]。為了兼顧計算機分析時間與仿真效果，仿真采用直徑8 mm的球體來作為土壤顆粒。采用的Hertz-Mindlin with Bonding模型中存在5個主要粘結參數，分別為：顆粒法向粘結剛度Sn、切向粘結剛度Sτ；粘結顆粒法向臨界應力δmax、切向臨界應力τmax以及顆粒粘結半徑Rb。在土壤顆粒半徑確定的情況下，通過材料密度與土壤含水率可計算得粘結半徑Rb[33]。參考該模型應用于土壤耕作方面的研究成果[24-26, 31-32]，其余4個粘結參數、各個材料之間的靜摩擦因數、動摩擦因數以及恢復系數如表3所示。

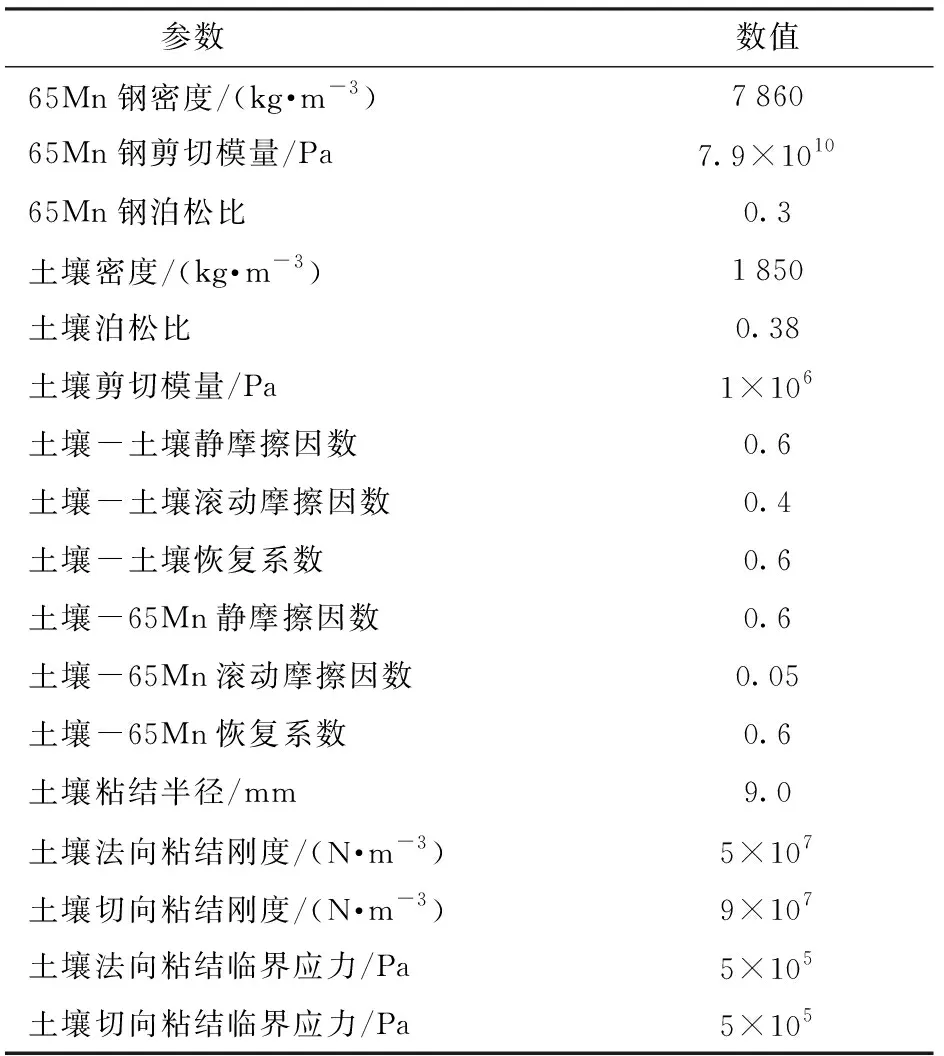
表3 材料性能參數與接觸參數Tab.3 Material performance parameters and contact parameters

2.3 運動仿真設計

將在SolidWorks 2018中建立的國標與仿生旋耕刀三維模型導入EDEM 2018軟件，構建長×寬×高為900 mm×300 mm×500 mm的土壤-旋耕刀相互作用模型(圖5)，然后在土槽仿真模型內生成24 000個直徑為8 mm的土壤顆粒模型。仿真分析中旋耕機刀軸轉速設定為150、200、250 r/min；前進速度為0.5 m/s；耕深為100 mm。整個過程分為2部分：0～0.6 s在土槽仿真模型內生成土壤模型；0.6～2 s旋耕刀分別以前進速度0.5 m/s以及刀軸轉速150、200、250 r/min與土壤模型進行切削運動，仿真數據保存間隔為0.001 s，共6組仿真試驗，在分析板塊獲取試驗結果，采用0.6～2.0 s內仿真數據，進行2種旋耕刀所受扭矩以及三向阻力的分析。

3 室內土槽旋耕試驗

2020年10月在南京農業大學浦口校區農機實習中心的土槽試驗臺車上進行國標與仿生旋耕刀扭矩采集試驗。土槽內土壤為黏土(質量分數分別為淤泥47%、黏土42%和沙11%)，取自南京市永寧鎮[34]。土壤經過調濕、夯實后，控制土壤平均含水率為16%，平均硬度為3.21×105Pa，且每次試驗時土壤參數保持一致。在對整個土槽試驗臺車系統檢查后，進行旋耕試驗。

3.1 試驗裝置

土槽試驗臺車主要由電機部分、試驗臺車、行走導軌、土槽、旋耕機、傳動系統、液壓系統部分、三點懸掛機構、各種傳感器、數據采集系統以及計算機等部分組成。土槽長×寬為24 000 mm×3 000 mm。土槽試驗臺車長×寬×高為2 500 mm×3 000 mm×2 000 mm，其結構簡圖如圖6所示。

3.2 土槽試驗

試驗采用江蘇清淮機械有限公司生產的旋耕機，總共安裝24把旋耕刀。土槽試驗臺車旋耕行走長度為18 m，旋耕機采用正轉且刀軸轉速設定為150、200、250 r/min 3擋，耕深保持100 mm，前進速度恒為0.5 m/s，分別測量2種旋耕刀在試驗過程中刀軸所受的扭矩。試驗現場如圖7所示。

4 試驗結果與分析

4.1 旋耕刀扭矩分析

仿真過程中旋耕刀在工作時總體上可分為4個過程。過程1，在旋耕刀未進入土壤時所受扭矩為0，在刀軸轉動下，側切刃進入縱切狀態，隨著入土深度增加，扭矩增大，接著主切刃進入橫切狀態，在主、側切刃與土壤共同作用時，扭矩出現驟然增加。過程2，當旋耕刀到達最大耕深時，扭矩達到最大值。過程3，旋耕刀越過最大耕深后，主、側切刃逐漸退出土層，扭矩慢慢減小。過程4，當主切刃完全退出土層時，在此過程中扭矩逐漸減小至0。

根據運動仿真分析得到2種旋耕刀所受扭矩的變化規律如圖8所示。3種刀軸轉速下國標旋耕刀所受的平均扭矩都比仿生旋耕刀高，刀軸轉速150 r/min時，分別為6.28、5.72 N·m，下降了8.87%；刀軸轉速200 r/min時，分別為7.75、7.32 N·m，下降了5.47%；當刀軸轉速達到250 r/min時，分別為11.03、10.49 N·m，下降了4.89%。由圖8可知，隨著刀軸轉速的增加，旋耕刀所受到的最大扭矩會逐漸變大。旋耕刀所受扭矩越大，所需功耗也越大，兩者之間呈正比關系[35]。

理想狀態下，土槽試驗臺車輸出扭矩等于旋耕機上24片旋耕刀所受的扭矩總和。但實際試驗中會出現各傳動機構間的摩擦以及其他部件產生扭矩。本文中將每次試驗所產生的額外扭矩都近似為相等，故土槽試驗臺車輸出扭矩等于所有旋耕刀所受的扭矩總和[32]。土槽試驗得到的平均扭矩信息如表4所示。試驗得出，在土槽試驗臺車前進速度和耕深保持一定時，3種刀軸轉速下仿生旋耕刀受到的平均扭矩都比國標旋耕刀小，分別降低了10.53%、4.46%、3.49%。通過將土槽試驗臺車輸出總扭矩除以旋耕刀數目近似得出每個刀片所受到扭矩。將仿生旋耕刀試驗與仿真平均扭矩結果進行對比分析，如圖9所示，2條曲線的相關系數為0.997且最大相對誤差為13.23%，旋耕刀所受的扭矩仿真值與試驗值變化趨勢相似，能夠較準確地反映旋耕機的功耗變化規律，但是由于土槽試驗受土壤中石沙、傳動系統摩擦以及土槽試驗臺車前進阻力等因素的影響[36]，其扭矩試驗值比仿真值大。

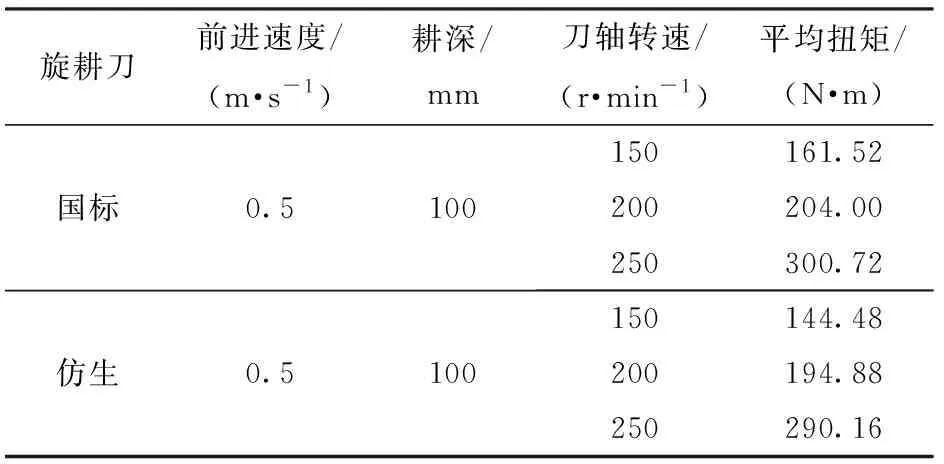
表4 土槽試驗中國標與仿生旋耕刀所受平均扭矩Tab.4 Average torque of national standard and bionic rotary blade in soil bin test

4.2 旋耕刀三向阻力分析

在旋耕作業中，定義兩種旋耕刀三向阻力方向分別為：水平作用力方向為X向、垂直作用力方向為Y向、側向作用力方向為Z向。則旋耕刀在土壤耕作中所受的三向阻力如圖10所示。圖中v為旋耕刀前進速度；ω為旋耕刀刀軸轉速；R為旋耕刀回轉半徑；Fx、Fy、Fz分別為旋耕刀所受的水平阻力、垂直阻力與側向阻力；M為驅動力矩。

通過仿真試驗得到國標與仿生旋耕刀所受到的三向阻力變化規律如圖11所示，在3種刀軸轉速下兩種旋耕刀旋轉1圈，其水平阻力Fx一直是正值，因為刀軸旋轉方向與旋耕刀前進方向相同。3種刀軸轉速下國標旋耕刀Fx最大值均比仿生旋耕刀大，在刀軸轉速為150 r/min時，仿生旋耕刀水平阻力最大值較國標旋耕刀降低了9.91%，分別為71.45、79.31 N；在刀軸轉速為200 r/min時，降低了5.78%，分別為93.55、99.29 N；在刀軸轉速為250 r/min時，降低了4.95%，分別為101.00、106.26 N。垂直阻力Fy呈先正后負的變化規律，主要是旋耕刀在達到最大耕深過程中向下切土，刀片受到垂直向上的阻力，為正值；當旋耕刀從最大耕深開始出土拋送土壤時，刀片受到垂直向下的力，為負值。在刀軸轉速為150 r/min時，仿生旋耕刀垂直阻力最大值較國標旋耕刀降低了9.09%，分別為53.00、58.30 N；在刀軸轉速為200 r/min時，降低了9.74%，分別為58.48、64.79 N；在刀軸轉速為250 r/min時，降低了6.38%，分別為70.86、75.68 N。側向阻力Fz一直為負值且3種刀軸轉速下國標旋耕刀側向阻力最大值均比仿生旋耕刀小。

由圖12可知，國標與仿生旋耕刀三向阻力最大值均隨著刀軸轉速的增加而升高，且仿生旋耕刀的水平阻力和垂直阻力最大值在3種刀軸轉速下都比國標旋耕刀小，但側向阻力最大值比國標旋耕刀大。

5 結論

(1)分析了東方螻蛄前足爪趾輪廓曲線特征，擬合4個爪趾上、下輪廓曲線的高斯方程的擬合度R2均不小于0.997 2，擬合誤差平方和SSE均不大于0.87。

(2)采用Hertz-Mindlin with Bonding土壤接觸模型用EDEM 2018離散元軟件構建了南方粘濕土壤-旋耕刀相互作用仿真模型，使用直徑為8 mm的球體模擬土壤顆粒，對2種旋耕刀進行受力分析。

(3)旋耕刀仿真受力分析表明，國標旋耕刀與仿生旋耕刀水平阻力、側向阻力和垂直阻力均隨著刀軸轉速的增加而增大，除側向阻力以外，仿生旋耕刀受到的水平阻力和垂直阻力的最大值都比國標旋耕刀小。在刀軸轉速為150、200、250 r/min時，仿生旋耕刀所受平均扭矩均比國標旋耕刀小，分別降低了8.87%、5.47%、4.89%。

(4)土槽扭矩對比試驗表明，在刀軸轉速為150、200、250 r/min時，仿生旋耕刀所受平均扭矩均比國標旋耕刀小，分別降低了10.53%、4.46%、3.49%。仿生旋耕刀所受平均扭矩的仿真值與試驗值變化趨勢相同，均隨著刀軸轉速的增加而增大，2條曲線相關系數為0.997，且最大相對誤差為13.23%，驗證了所建立的離散元仿真模型的有效性。