V形布局地形上不同頻率入射波的布拉格共振特性研究

涂俊豪，陶愛峰，蘇俊瑋，徐 嘯，張海明

（1.海岸災害及防護教育部重點實驗室（河海大學），江蘇 南京 210024；2.河海大學 港口海岸與近海工程學院，江蘇 南京 210024）

0 引言

由于能源短缺問題日益嚴重，大力發展可再生能源成為世界各國的共識。波浪能具有環保可再生、能量密度高等優勢，開發利用波浪能，成為解決能源問題的重要突破口。人們對波浪能利用的研究已有百年歷史，大多數學者通過對波能發電裝置的改進和陣列布局優化來提高發電裝置的發 電 效 率[1]～[5]。近 年 來，有 學 者 發 現，可 以 通 過 布 拉格共振來提高波浪能量密度，從而來提高發電裝置的發電效率。

1915年，布拉格父子發現，當X射線的波長為晶體間距的兩倍時，X射線的反射最強，這種波列的相關干涉，被稱為布拉格共振[6]。Davies A G[7]發現，特定波長的表面重力波會與連續的正弦周期地形發生共振，即使沙波波高不大，表面重力波的振幅也會在發生共振以后大幅增加。Elandt R B[8]發現，可以借助布拉格共振驅動雙層密度流體的表面波能量向界面波傳遞，從而保護浮式建筑物；同時，Elandt R B提出，可以利用布拉格共振，讓表面重力波的能量匯聚，從而提高波浪能量密度和發電裝置的發電效率。Tao A[9]通過波浪水槽試驗發現，利用布拉格共振來提高波浪能量的密度，可以將發電裝置的發電功率提升10倍以上。蘇俊瑋[10]基于高階譜方法發現，當地形呈V形布局的連續正弦時，波浪與地形發生布拉格共振反射后，地形前方會產生聚焦效應，波浪振幅增幅較二維地形顯著增大。但是，該研究只考慮了共振最強狀態對應的入射波布拉格共振引發的波能聚焦特性，而真實的波浪由不同頻率的波組成。

因此，本文采用文獻[10]中的數學模型進一步研究了在二維布拉格共振的共振主頻附近，V形布局地形在不同頻率入射波下 （保持地形波陡與入射波波陡不變）的布拉格共振聚焦特性，研究的成果可為布拉格共振發電的實際應用提供理論參考。

1 波浪與地形的耦合模型及驗證

利用不同頻率的規則波進行正向入射和斜向入射（以 θ=19.47°為例，其中 θ為地形法線和入射波的夾角），以復演文獻[11]中的兩組布拉格共振數值模擬試驗，并求得不同頻率下的反射系數R，將模擬結果與文獻[11]的攝動理論結果進行對比，結果見圖1。從圖1可以看出，數值模擬結果與理論曲線吻合良好，證實了模型計算結果的可靠性。

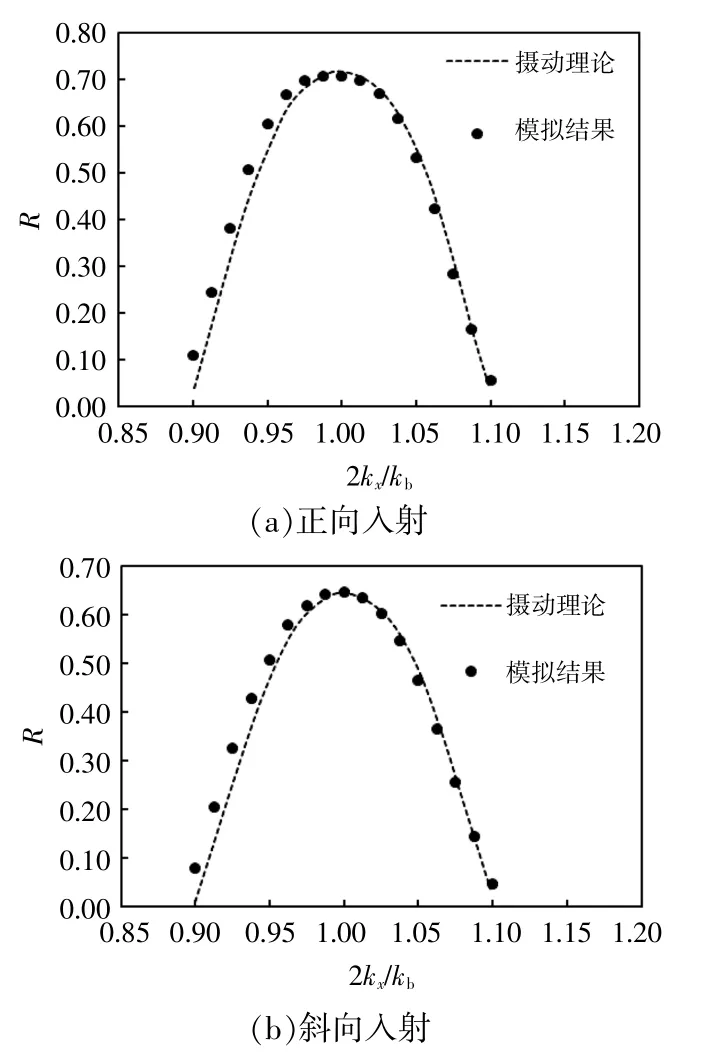
圖1 不同頻率的布拉格共振反射系數Fig.1 Bragg resonance reflection coefficients at different frequencies

2 數值模擬

本節將具體介紹本次模擬的基本參數、入射波參數、地形參數和模擬組次的設置情況。下文中：kx為入射波x方向上的波數；kb為地形波數；T，A，L和k分別為入射波的周期、振幅、波長和波數；d為地形振幅；h為水深。

2.1 模型基本參數

模型計算區域的大小為32 m×32 m，共512×512個計算節點。按每周期T/Δt=64的時間步長進行模擬，共模擬波浪傳播TS/T=20個周期。相關參數按照文獻[11]進行設置，非線性階數M=3。

2.2 入射波設置

在本文中，入射波的初始波面和勢函數按微幅波理論進行計算，同時保證各組頻率下入射波的波陡相等，即kA=0.05。按長度轉換無量綱參數L′/L=2π/32，將 所 有 參 數 無 量 綱 化。

2.3 地形設置

根據文獻[10]的研究，各組頻率入射波對應的V形 布 局 地 形 的 夾 角 α為90～180°。d，h，kb滿 足d/h=0.31，kbd=0.16。圖2為V形地形在空間布局的立面圖（總體以y=16 m對稱，以V形地形的頂點為x方向的坐標原點，并向著來波方向增大，ξ為地形高度）。

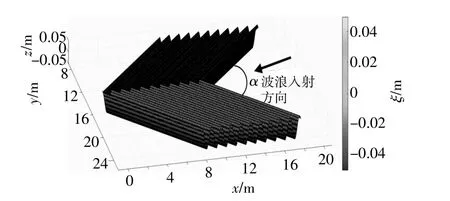
圖2 起伏地形空間布局立面圖Fig.2 Stereoscopic schematic diagram of rippled bottom spatial layout

本研究通過改變2kx/kb來改變入射波的頻率，考慮到大部分海浪譜為單峰譜，且譜寬較窄，所 以 當2kx/kb＞1.1或2kx/kb＜0.9時，布 拉 格 共 振 的波浪反射率 （反射率的大小等于反射波高與入射波高的比值）雖然會增大但仍較小，而且對應頻率的入射波能量較小。因此，本文研究的頻率為2kx/kb=0.9～1.1。

2.4 模擬組次

綜合前文討論，本文研究的入射波頻率為2kx/kb=0.9～1.1，從中均勻取17個頻率，研究的V形布局地形的夾角α為90～180°，從中取15個角度，共構成255組模擬組次。

3 結果與分析

入射波會與連續正弦地形發生共振反射，反射波經由V形布局地形匯聚，在地形前方與入射波疊加，形成不完全立波。振幅顯著增大的點組成的區域，被稱為波能聚焦區。20個周期內有效波高Hs與初始波高H比值（Hs/H）最大的點被稱為波能聚焦點。通過對比各模擬組次波能聚焦點的Hs/H，找出各頻率入射波對應V形布局地形的最優夾角，并探究最優V形布局地形夾角下，各頻率入射波的波能聚焦區分布及波能聚焦點的運動特性。

3.1 入射波對應V形布局地形的最優夾角

根據模擬結果，計算出模擬計算區域內512×512個計算點20個周期內的有效波高，各模擬組次波能聚焦點的Hs/H如圖3所示（為了清晰地表示波能聚焦點的Hs/H與頻率和V形布局地形夾角 的 關 系，以2kx/kb=0.9，0.95，1，1.05，1.1的5組頻率入射波的模擬組次結果為例畫圖）。從圖3可以看出：隨著V形布局地形夾角 α的逐漸增大，波能聚焦點的Hs/H先增大后減小；當2kx/kb偏離1較少時，波能聚焦點的Hs/H最大值對應的 α=162.24°；當2kx/kb偏離1較多時，波能聚焦點的Hs/H最大值對應的 α不等于162.24°。

圖3 波能聚焦點的Hs/H隨α的變化曲線Fig.3 The variation of Hs/H at wave energy focusing point as a function ofα

不同 α下，波能聚焦點的Hs/H隨入射波頻率的變化曲線如圖4所示。從圖4可以看出：當α=90°時，入射波的反射率為零，各頻率入射波的波能聚焦點的Hs/H均很小；在不同 α下，波能聚焦點的Hs/H均隨著頻率的增大而呈現出先增大后減小的變化趨勢。結合圖1和文獻[10]的研究可知，當2kx/kb偏離1較大或 α接近90°時，波浪的反射率較小，布拉格共振作用較弱，波能聚焦點的Hs/H均較小，模擬結果易受到水深變化引起的波浪非線性作用等因素的影響，因此，模擬結果不能較好地反映布拉格共振的特性。由此可以得到結論，在本文的研究頻率范圍內，各頻率入射波對應V形布局地形的最優夾角均相等，且α=162.24°。因此，本文將進一步研究最優V形布局地形夾角下，不同頻率入射波的布拉格共振特性。

圖4 波能聚焦點的Hs/H隨入射波頻率的變化曲線Fig.4 The variation of Hs/H at wave energy focusing point as a function of incident wave frequency

3.2 入射波的波能聚焦區的Hs/H分布

通過統計計算區域內各計算點20個周期內的波動數據，得到各計算點的有效波高，將各點的有效波高與初始波高進行對比，可知各點的Hs/H如圖5所示。從圖5可以看出：當2kx/kb偏離1較大時，波高增大區域主要集中在地形上方；當2kx/kb接近1時，布拉格共振作用較強，大量反射波由V形布局地形聚焦后，在地形前方形成波能聚焦區。由于地形對稱布置，發生布拉格共振反射時，有效波高分布也以y=16 m為對稱軸對稱分布。波浪由V形布局地形反射以后，能量向對稱軸聚焦，因此對稱軸上的波能聚焦區的Hs/H最大，并向著兩側逐漸降低，波能聚焦點的位置在對稱軸上。因此，本文將繼續研究對稱軸上的波能聚焦點的Hs/H分布。

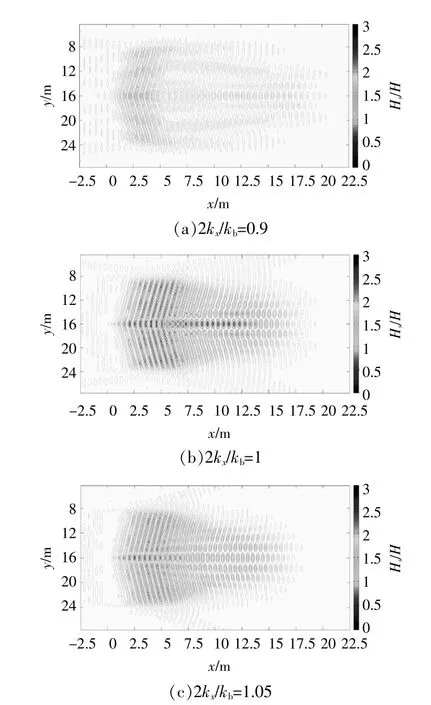
圖5 不同頻率入射波的波能聚焦區的Hs/H分布Fig.5 Spatial distribution of Hs/H within the wave energy focusing region at different incident wave frequencies

在對稱軸上-2.5～22.5 m的范圍內，各計算點的有效波高如圖6所示（以地形結束位置為0，地形前方為正）。從圖6可以看出：當2kx/kb接近1時，布拉格共振反射率較大，地形前方有一系列波高明顯增大且Hs/H相近的點，這些點分布在對稱軸上5 m（對稱軸上地形起始邊界位置）后的第1～15個波峰點之間；當2kx/kb偏離1較大時，布拉格共振強度和反射率均較低，地形前方的Hs/H沒有明顯增大，整個計算區域內Hs/H最大點在地形上方，這是因為水深變化而產生的波浪非線性作用對波高的影響較大，故本文不作分析。由此推測，若入射波是不規則波，則波能聚焦點在V形布局對稱軸上x=5～12 m處。

圖6 對稱軸上-2.5～25 m之間的計算點的Hs/H分布Fig.6 Hs/H distribution on symmetrical axis between-2.5～25 m

3.3 波能聚焦點的位置及運動特性

當α=162.24°時，不同頻率入射波的波能聚焦點的位置如圖7所示（以地形結束位置為0，地形前方為正）。

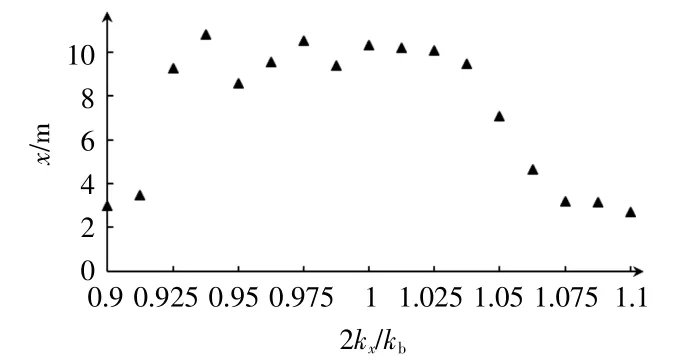
圖7 最優V形布局地形夾角下，不同頻率入射波的波能聚焦點的位置Fig.7 The positions of wave energy focusing point at different incident wave frequencies under the condition of optimal V-shaped bottom angle

從圖7可以看出：當2kx/kb＜1時，隨著2kx/kb逐漸增大，波能聚焦點的Hs/H逐漸增大，波能聚焦點的位置逐漸從地形上方向地形前方移動；當2kx/kb＞1時，隨著2kx/kb逐漸增大，波能聚焦點的Hs/H逐漸減小，波能聚焦點的位置逐漸靠近地形；當0.925≤2kx/kb＜1.05時，波能聚焦點在對稱軸上x=10 m附近，此時波能聚焦點的Hs/H最大，且波能聚焦點的位置在地形前方相差不大。因此，下文將繼續討論該頻域內波能聚焦點的運動特性（以2kx/kb=0.95，1和1.05時 為 例）。

圖8為波能聚焦點的波面時間序列圖（η為波面高程）。當波能聚焦點處于穩定狀態時，每相鄰周期的波峰值不相等。因此，本文選取20個周期內各計算點的有效波高來反映各點的能量大小。波能聚焦點達到穩定狀態所需時間與穩定狀態的Hs/H值成正比，穩定狀態的波高增幅越大，達到穩定所需的時間越長。

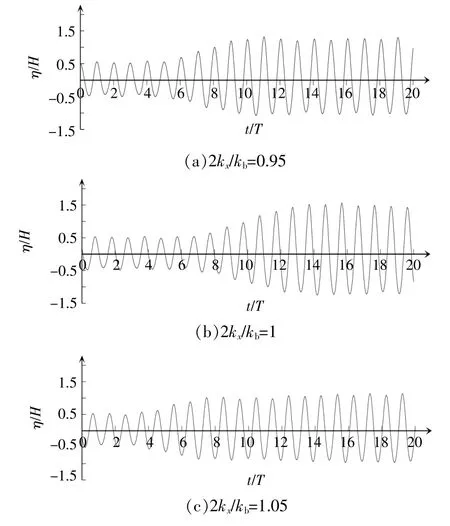
圖8 波能聚焦點的波面時間序列Fig.8 Time series of free-surface elevation at wave energy focusing point

4 結論

本文基于高階譜方法，討論了不同V形布局地形對不同頻率入射波的影響特性，找出了各頻率入射波對應的最優V形布局地形夾角，并探究了最優V形布局地形夾角下，各頻率入射波的波能聚焦區分布及波能聚焦點的運動特性，得到以下結論。

①對于不同頻率的入射波，隨著V形布局地形夾角 α的增大，波能聚焦點的Hs/H呈現出先增大后減小的變化趨勢，并且當 α=162.24°時，各頻率入射波的波能聚焦點的Hs/H均達到最大，因此，各頻率入射波的最優V形布局地形夾角為162.24°。

②在最優V形布局地形夾角下，各頻率入射波的波能聚焦區均對稱分布，且對稱軸上的波能聚焦區計算點的Hs/H最大。當2kx/kb偏離1較大時，波能聚焦區主要分布在地形上方；當2kx/kb接近1時，波能聚焦區主要分布在地形前方。

③當2kx/kb接近1時，在波能聚焦區對稱軸上存在一系列增幅明顯增大且增大倍數相近的計算點，這些計算點分布在15個立波波長范圍內，且波能聚焦點位于x=10 m附近；當2kx/kb偏離1較大時，波能聚焦點位于地形上方。

本文只研究了V形布局地形下不同頻率規則波的布拉格共振特性，不規則波可以看成由多組不同頻率規則波按不同海浪譜組合而成。當入射波為不規則波時，V形布局地形上的布拉格共振特性，還有待探討。