基于風電機組無功裕度預測的風電場無功分層控制策略

劉穎明，劉闖闖，王曉東

（沈陽工業大學 電氣工程學院，遼寧 沈陽 110870）

0 引言

大規模風電場并網會造成電網電壓波動，通過控制雙饋式風電機組（Doubly-Fed Induction Generator，DFIG）及靜止無功發生器（Static Var Generator，SVG）可以維持并網點 （Point of Common Coupling，PCC）的電壓穩定，明顯改善電壓波動[1]。文獻[2]為解決并網風電場無功電壓調節易受風功率波動影響的問題，提出了基于分層模型預測控制的電壓協調控制策略，有效抑制了PCC電壓波動，但未考慮機組有功輸出與無功輸出的內在聯系。文獻[3]推導出DFIG無功輸出極限關系式，然而當DFIG以其自身無功極限進行無功補償時，將有可能因輸出功率越限而脫網，從而導致電網電壓波動。文獻[4]為風電機組預留出無功裕度，分析了風電場無功裕度與其當前無功功率的關系，通過協調控制避免了無功越限的發生。文獻[5]提出等裕度無功分配策略，有效防止了變流器電流越限發生跳機的現象，但未考慮無功調節過程中調節指令的低時效性問題。在預測算法方面，文獻[6]提出了一種小波變換、支持向量機和粒子群的混合模型，但與傳統交叉驗證法相比，精度并沒有提升太高。文獻[7]提出了基于改進的經驗小波變換和最小二乘支持向量機的混合預測模型，并通過鳥群算法對參數進行聯合優化，提高了預測性能。上述研究對雙饋式風電機組無功調節能力和風電場無功裕度的計算與應用進行了有益探索，但在利用風電機組無功調節能力進行電網電壓調節時，都未將無功控制指令的時效性、風電功率的預測與實時校正、風電機組出口電壓的波動性考慮在內。

本文以雙饋式風電機組為研究對象，采用混合預測算法進行風電功率預測，同時提出了一種預測功率的實時校正方法，并由校正后的有功功率預測值計算風電機組的無功裕度預測信息，進而提出基于風電機組無功裕度預測的風電場無功分層控制策略。在風電場層面，無功分層控制以并網點電壓偏差和線路有功損耗最小為目標，求解風電場無功參考值；在風電機組層面，以風電機組的出口電壓波動最小和預測無功裕度最大為無功分配依據，向場內DFIG和SVG下發無功任務，從而改善電網和機組出口電壓并為風電場預留出充足的無功裕度。最后以實際算例仿真驗證所提控制策略的可行性。

1 風電場無功分層控制模型

本文提出的無功控制策略分三層實現，即風電場的電壓求解層、無功整定層和無功分配層，其控制原理框架如圖1所示。

圖1 風電場無功分層控制原理Fig.1 Reactive power layered control principle of wind farm

各層和功能模塊在滾動周期和指令執行周期的時間分辨率如表1所示[8]。其中，風電功率預測模塊超短期風電預測為15 min預測，1 min采集一次機組實時輸出有功功率，在滾動周期內共執行15次預測校正。

表1 時間分辨率Table 1 Time resolution table

2 風電場無功分層控制策略

2.1 最優并網電壓求解

①并網電壓偏差最小

風電場并網點處的電壓須要滿足電網要求，具有良好的跟蹤特性[9]，因此選擇并網點電壓Upcc與參考電壓差最小目標為

②線路有功損耗最小

風電場內風電機組的線路有功損耗最小時有 [9]：

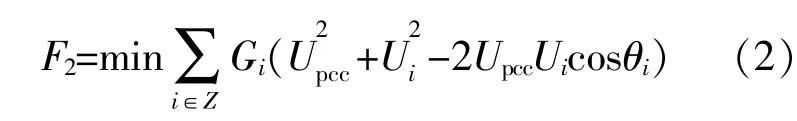
式中：Z為與PCC相鄰的節點數；Gi為PCC與節點i之間線路的電導；Ui為節點i處的電壓幅值；θi為PCC與節點i之間實測的電壓相角差。

③PCC潮流約束方程

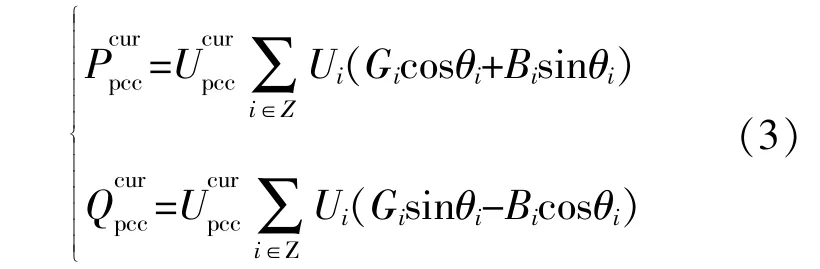
為了防止風電場脫網運行，節點電壓須要維持在額定值-3%～7%，即：

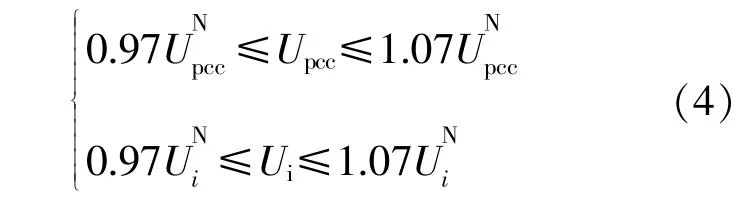
④目標函數

并網點電壓偏差和線路有功損耗最小的多目標，通 過 權 重 系 數 λ（0＜λ＜1）可 轉 換 為 單 目 標 優化，λ要綜合考慮并網點電壓偏差和線路有功損耗兩個子目標對總目標函數的貢獻權重。綜上，目標函數為

⑤模型求解

本文的優化模型能夠表述為標準二次規劃（Quadratic Programming，QP）問題，采用Matlab進行實時在線優化求解，得到滿足約束條件的實時最優并網點電壓，并以此作為計算風電場無功參考值的電壓參考信號[10]，[11]。QP的系數矩陣H和f分別為

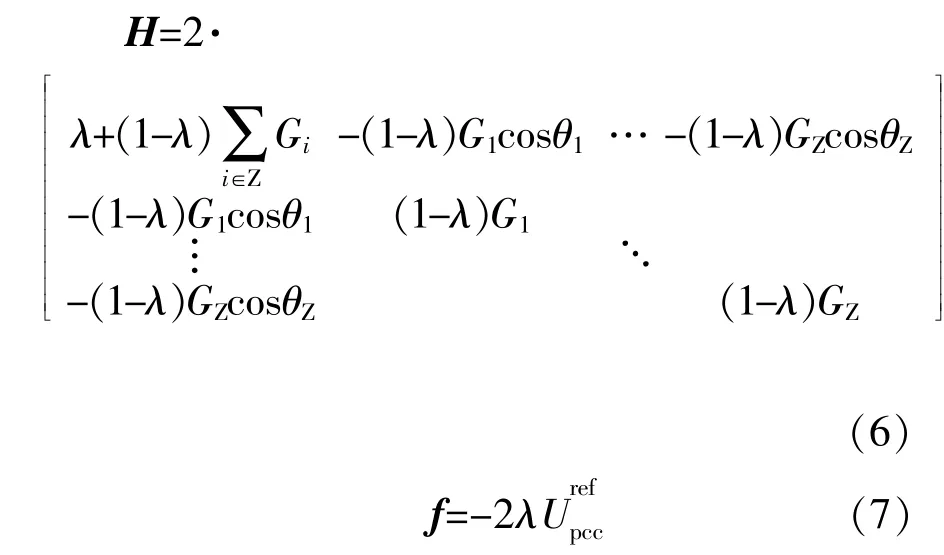
2.2 風電場無功參考值求解

比例積分（Proportion Integration，PI）控制器可以消除電壓的穩態誤差[12]。將并網最優電壓與PCC當前電壓做差，求得偏差電壓ΔU，通過PI控制器得到風電場無功參考值，具體過程如圖2所示。

圖中：Tr為電壓測量滯后時間常數，用于模擬采樣延時；Tc為與各個DFIG的通信延遲等相關的時間常數用于模擬輸出延時；KP和KI分別為PI環節中的比例積分系數；Qmax和Qmin分別為風電場輸出無功的上、下限，當輸出越限時以限值為輸出量。

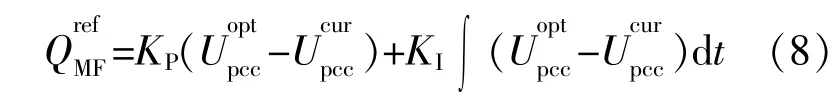
式中：KP≈U/X，X為并網點與風電機組匯集母線之間輸電線路的電抗[12]；KI依據經驗整定。

2.3 基于無功裕度預測的無功優化分配

2.3.1基于EWT-LSSVM的風電功率預測

風電功率預測可以有效消除風電功率波動帶來的影響，提高風電并網可靠性。本文采用文獻[7]所提方法進行風電功率預測。首先將原始信號通過經驗小波變換（Wavelet Transform，EWT）分解，得到更具規律性和平穩性的分量，該分量作為最小二乘支持向量機（Least Square Support Vector Machine，LSSVM）的輸入，LSSVM對各分量分別進行預測以提高預測精度，最后將各分量預測結果進行重構得到預測值。預測過程如圖3所示。

圖3 風電功率預測框圖Fig.3 Wind power prediction block diagram

選取歷史風電功率數據作為原始信號f（t），EWT方 法 將f（t）分 解 為K個 固 有 模 態 分 量[7]，其中各模態分量為

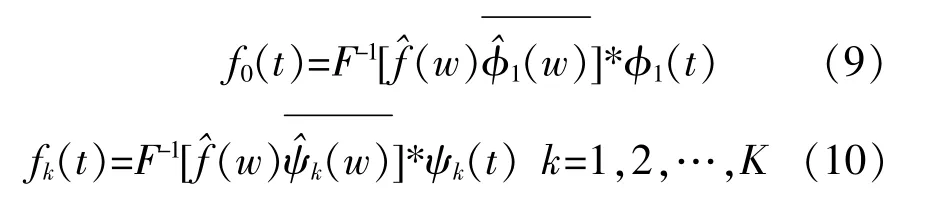
得到的模態分量作為LSSVM的訓練樣本數據（xi，yi），i=1，2，…，L，L為 訓 練 樣 本 長 度。LSSVM將傳統支持向量機中二次規劃問題轉化為線性方程 組 求 解[7]，簡 化 了 求 解 的 過 程，對 于（xi，yi）滿 足線性方程組：

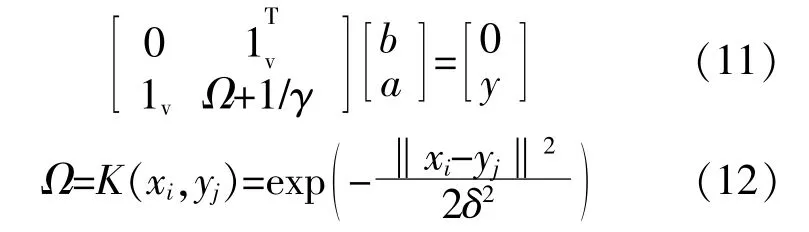
式 中：1v=[1，1，…，1]T；γ為 正 則 化 參 數；b為 偏 差項；a為 拉 格 朗 日 乘 子，a=[a1，a2，…，aL]T；y為 樣 本輸 出 值，y=[y1，y2，…，yL]T；Ω為 核 函 數，本 文 取 為 徑向基核函數；δ為核函數的帶寬。

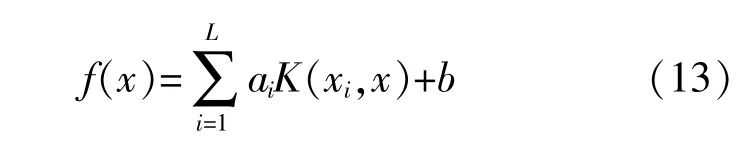
對于新的樣本x，訓練后的LSSVM模型輸出為式 中：ai，b由 式（11）和（12）求 解 得 出。

最后將各分量預測結果進行疊加，得到最終的風電功率預測信息。

2.3.2預測功率校正

預測功率校正能夠使預測更接近實際風電。校正功率、超短期預測功率與實際功率之間的誤差e1，e2分 別 為

此外，為保證功率輸出快速逼近實際功率，取實時校正功率為

考慮功率校正后的預測功率為

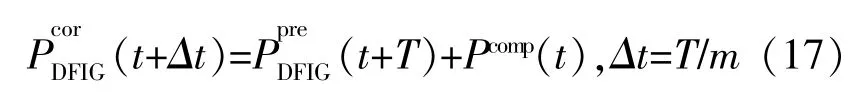
式中：T為超短期風電功率預測周期時長，T=15 min；Δt為校正周期時長；m為校正次數，本文m=15。

2.3.3無功優化分配目標函數

式中：Δt′為DFIG無功控制周期時長，本文Δt′=Δt/12；Q（t+Δt′）為Δt′時刻后機組待發無功功率的參 考 值 ；QDFIGi，max和QDFIGi，min分 別 為 機 組 的 最 大 和最小無功極限。

由AVC實時測得各DFIG的無功功率和電壓 分 別 為QDFIGi（t）和UDFIGi（t），上 一 無 功 控 制 周 期的 無 功 功 率 和 電 壓 分 別 為QDFIGi（t-Δt′）和UDFIGi（t-Δt′），則 第i臺DFIG無 功 電 壓 靈 敏 度 為

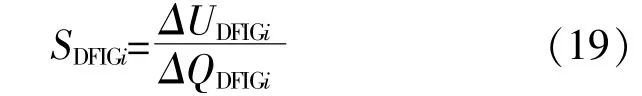
由于Δt′很小，可認為在Δt′時間內無功電壓靈 敏 度 變 化 不 大，SDFIGi（t+Δt′）≈SDFIGi（t），即：

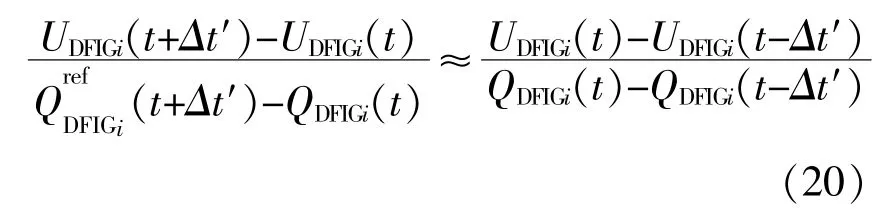
由 式（20）可 得t+Δt′內 電 壓 波 動 為

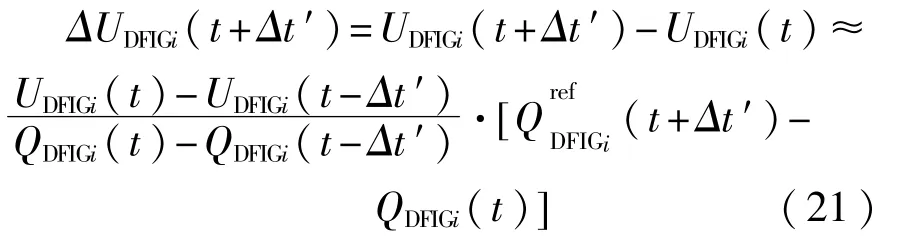
以t+Δt′時刻風電機組的出口電壓波動最小和預測無功裕度最大為無功分配原則，通過引入權 重 系 數γ（0＜γ＜1）并 對 第 二 個 子 目 標 取 負 值，將多目標求解問題轉換為單目標最小值優化問題。為了便于使用二次規劃求解，取目標函數為

2.3.4約束條件

各DFIG在t+Δt′時刻輸出的無功功率應小于預測無功極限，即：

當DFIG能夠滿足風電場無功需求時，優先考慮DFIG輸出，此時DFIG所發無功應滿足：

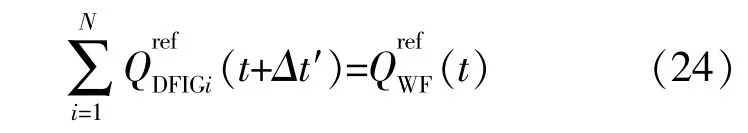
當DFIG無功無法滿足風電場無功需求時，以預測無功極限值輸出：

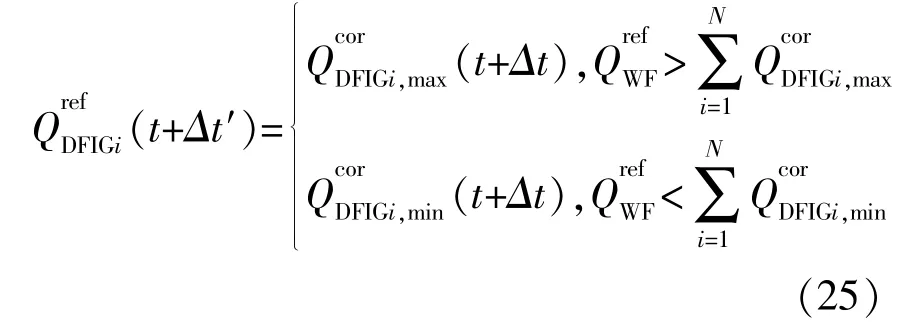
剩余無功由SVG承擔，即：

3 算例分析

為驗證所提方法的有效性，本文以遼寧108 MW雙饋風電場為例，其拓撲如圖4所示。

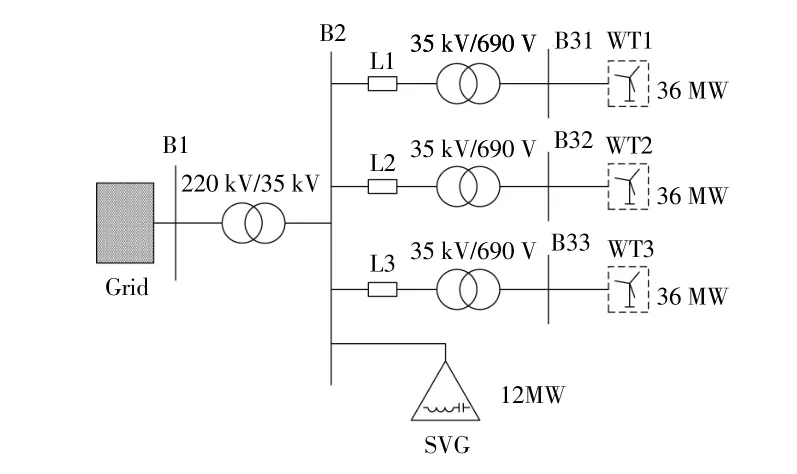
圖4 算例仿真模型Fig.4 Case simulation model

風電場由3臺36 MW等值風電機組（WT）和12 MVar SVG組成，其中36 MW等值風電機組由24臺參數相同的1.5 MW雙饋式風電機組組成。風電場通過35 kV/220 kV變壓器并入到電網。本文不考慮地形和葉片尾流對風速的影響，設定每臺等值風電機組在不同風速下運行。在QP求解中，權重系數選取綜合考慮子目標對總目標函數的 貢 獻，本 文λ=1-1/∑Gi≈0.9，γ=0.8。

3.1 校正后風電功率預測效果分析

等值風電機組WT3的預測效果如圖5所示。

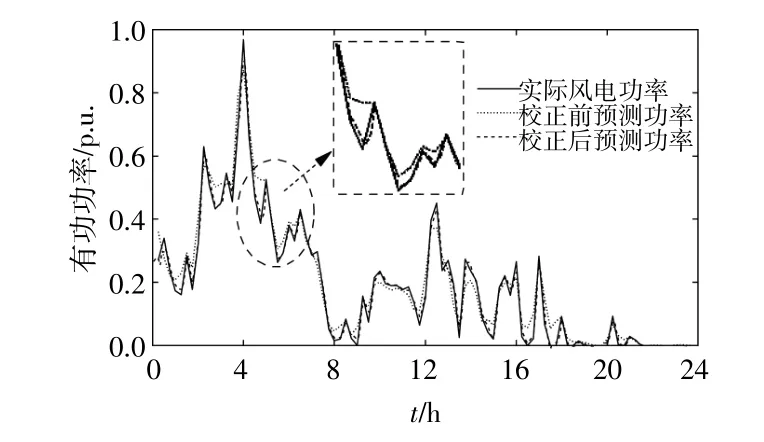
圖5 WT3的實際、預測與校正后風電功率對比Fig.5 Comparison of actual，predicted and corrected wind power of WT 3

由圖5可知，校正后的風電功率預測曲線與實際功率曲線更加接近，預測效果更好。

功率預測曲線的歸一化均方根誤差（Normalized Root Mean Square Error，NRMSE）和 歸 一 化平均絕對誤差（Normalized Mean Absolute Error，NMAE）評估結果如表2所示。

表2 預測精度比較Table 2 Comparison of forecasting accuracy

由表2可知，所提預測功率校正方法取得了良好的預測效果，可以應用于風電機組無功裕度預測信息的實時求解過程。

3.2 策略控制效果分析

為分析不同控制方式對風電機組出口電壓和無功裕度的影響，并驗證所提出的優化控制策略，本文采用以下兩種控制方式進行仿真對比。①傳統比例控制策略 （Traditional Proportional Control Strategy，TPCS），以并網點電壓偏差和線路有功網損最小為目標，不考慮風電功率預測信息，按各DFIG和SVG的無功容量對風電場內DFIG和SVG進行比例無功分配。②本文優化控制策略（Article Optimal Control Strategy，AOCS），利 用 本文提出的基于無功裕度預測的無功分層控制策略進行風電場無功任務的優化分配。

圖6 不同控制策略下WT的出口電壓對比Fig.6 Comparison of wind turbine outlet voltage under different control strategies

為了驗證WT出口電壓穩定性，取標準差（σ）指標進行評估，評估結果如表3所示。

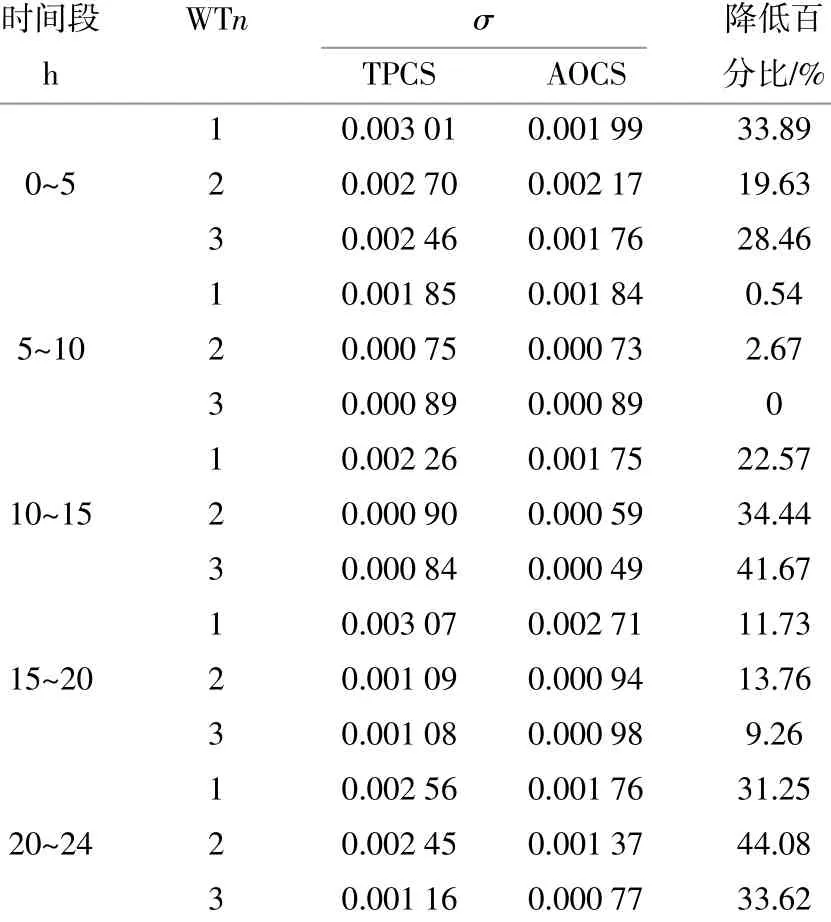
表3 1 d內不同控制策略下的電壓波動性評估結果Table 3 Evaluation results of voltage fluctuation under different control strategies in one day

由圖6和表3可知，傳統控制策略由于未能預知未來功率波動而提前做出規劃調整，電壓波動較大。本文所提策略在無功控制過程中將實時校正的預測風電功率，根據每臺風電機組未來時段內的功率波動信息合理規劃分配無功指令，實現控制周期內無功的協調優化，降低了風電機組出口電壓的波動性。對于1 d內風電場整體的控制效果而言，采用基于功率預測的優化控制策略具有較小的標準差，風電機組出口電壓波動性較小、穩定性更高，電壓波動的標準差最大減小44.08%，平均減小21.76%。

3.3 風電機組無功出力分析

根據本文所提的無功裕度計算方法，得到風電機組預測無功極限與實際輸出無功功率對比，如圖7所示。

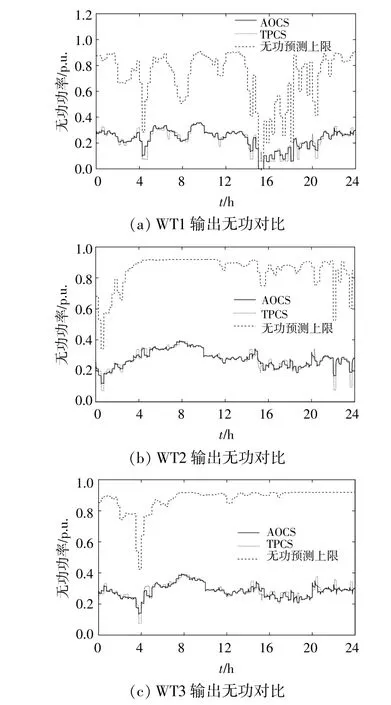
圖7 風電機組輸出無功功率極限與實際輸出對比Fig.7 Reserved reactive power margin under different control strategies in a day

由圖7可知，采用本文優化控制策略進行機組無功分配，各機組根據相應的預測無功極限進行無功出力，在無功調節過程中，高無功發生能力的風電機組承擔相對較多的無功任務，充分發揮了DFIG的無功調控能力。

計算1 d內AOCS和TPCS策略控制下各WT的預留無功裕度，結果如表4所示。

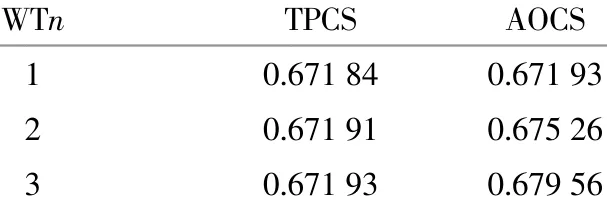
表4 1 d內不同控制策略下的預留無功裕度Table 4 Reserved reactive power margin under different control strategies in a day

由圖4可知，本文所提控制策略預留出了相對多些的無功裕度，其中WT3比傳統控制多出1.12%，說明依據預測無功極限協調機組無功出力可以在一定程度上增加風電場的無功裕度。

4 結論

針對風電場無功控制時效性低的特點，本文提出了一種基于風電機組無功裕度預測的風電場無功分層控制策略。該策略預測誤差在NRMSE評估指標中由平均4.99%降低到2.11%，在NMAE評估指標中由平均3.72%降低到1.61%，提高了預測的精度。本文提出的分層協調控制策略，分別實現了對風電場和風電機組兩個層面的優化處理，通過引入校正后的功率預測信息，提高了無功控制指令的時效性，有效地協調了各機組無功出力，在為各風電機組預留出相應無功裕度的同時，降低了風電機組出口電壓波動性，電壓波動的標準差最大減小44.08%，平均減小21.76%。