新型憶阻光伏電池的建模與分析

董 軍，石 杰，高明煜，孫平遠

（1.杭州師范大學 材料與化學化工學院，浙江 杭州 311121；2.杭州電子科技大學 電子信息學院，浙江杭州 310018；3.浙江大學 電氣工程學院，浙江 杭州 310027）

0 前言

近年來，為解決能源危機、環境污染和經濟發展等問題，新能源發電系統及相關技術快速發展。光伏發電系統因其清潔、環保、儲量豐富等優點在新能源發電系統中脫穎而出[1]，[2]。光伏電池是光伏發電系統的關鍵設備，光伏電池的建模與仿真對光伏發電系統的綜合性研究非常重要。目前，光伏電池的仿真模型主要分為兩類，分別為基于等效電路法的物理模型和基于函數擬合法的行為模型[3]～[8]。其中：基于等效電路法的物理模型易受環境溫度和太陽輻射強度的影響，因此，其輸出特性具有明顯的時變特征；基于函數擬合法的行為模型在構建過程中須要大量的實時數據作為支撐，當外部環境發生變化時，基于函數擬合法的行為模型須要不斷地調整擬合函數中可變參數的取值，以保證擬合精度滿足要求。綜上可知，與基于等效電路法的物理模型相比，基于函數擬合法的行為模型能夠更好地描述光伏電池的輸出特性。但是，基于函數擬合法的行為模型并不適用于實際的應用研究[9]。因此，建立一種既貼近光伏電池的物理特性，又能對光伏電池動態過程進行自適應描述的建模方法，是一項具有挑戰的工作。

1971年，Chua L基于電路理論公理化體系的完備性闡述定義了憶阻器的概念[10]。2008年，Tour J M發明了憶阻器[11]。學者們通過實驗發現，憶阻器具有獨特的開關轉換機制、自動的記憶功能、連續的輸入輸出特性，這些特性使得憶阻器在非易失性存儲器、人工神經網絡、大規模集成電路等 方 面 有 著 巨 大 的 應 用 潛 力[12]～[15]。

本文基于光伏電池的物理模型和憶阻器的非線性特性，運用憶阻器分別替代光伏電池經典模型中的二極管和旁路電阻，構建了兩類新型憶阻光伏電池模型；然后，通過嚴謹的數學推導對這兩類模型的輸出特性進行深入研究，并通過一系列的數值仿真驗證了本文方案的有效性和科學性。由于憶阻器對參數的敏感性，使得憶阻光伏電池模型具備一定的時變特性，這一特性能夠較好地解決傳統光伏電池建模過程中存在的自適應性弱、無法完全展現光伏電池輸出特性的問題。

1 憶阻光伏電池模型

光伏電池輸出特性易受外界環境變化的影響。為了更加準確地描述外界環境（環境溫度和太陽輻射強度）對光伏電池輸出特性的影響，以及為光伏陣列拓撲結構和最大光伏功率點跟蹤算法的設計提供理論基礎和實驗支撐，本文基于經典的光伏電池模型和憶阻理論，提出了兩類新型憶阻光伏電池模型。

1.1 光伏電池模型

根據量子學理論[1]，光伏電池等效電路模型可以分為3種，分別為光伏電池的理想模型、簡化模型和實際模型。光伏電池等效電路模型如圖1所示。圖中：IPV為光生電流 （與太陽輻射強度成正比），A；ID為 流 經 二 極 管 的 電 流，A；Rs為 理 想 模 型串聯電阻（用于表示不可忽略的阻抗效應），Ω；Rp為簡化模型的旁路電阻 （用于表示模擬光伏電池中漏電流導致的漏電阻等實際現象），Ω；I為流經光伏電池負載的電流，A；V為光伏電池兩端的電壓，V。

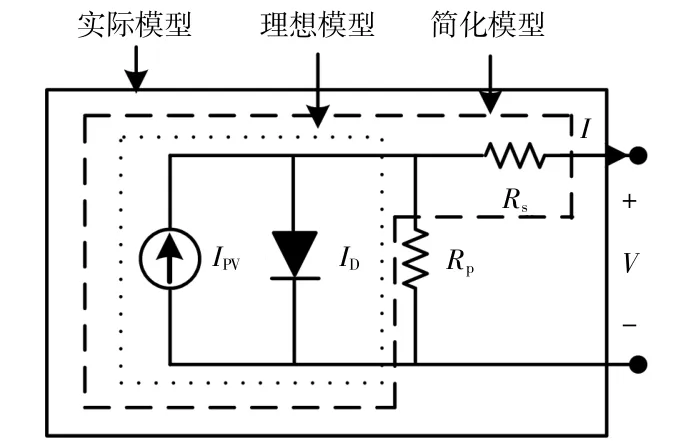
圖1 光伏電池等效電路模型Fig.1 The equivalent circuit model of photovoltaic cell

由圖1可知：理想模型為最簡單的電路模型，其電壓、電流表達式有利于清晰地展示光伏電池的基本特性；簡化模型在理想模型的基礎上增加了串聯電阻Rs；實際模型在簡化模型的基礎上增加了旁路電阻Rp。根據基爾霍夫電流定律，光伏電池理想模型、簡化模型和實際模型的伏安特性關系表達式分別為[1]

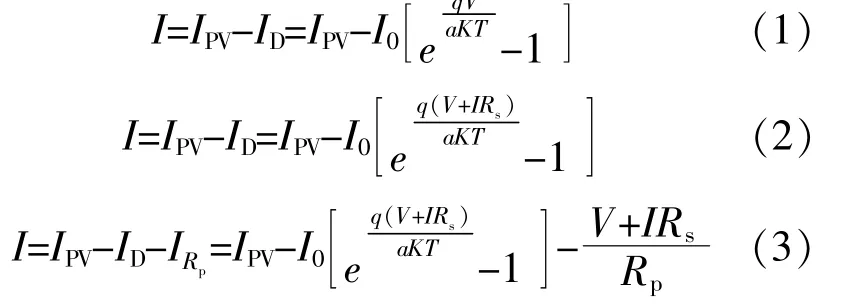
式中：I0為光伏電池反向飽和電流，A；q為電子電荷，取1.6×10-19C；K為 波 爾 茲 曼 常 數，取1.38×10-23J/K；T為絕對溫度；a為P-N結的理想因子；IRp為流經旁路電阻Rp的電流，A。

1.2 憶阻光伏電池模型

1.2.1憶阻器

憶阻器作為一種具有記憶功能的無源非線性二端元件，其阻值能夠根據供給電源的強度、極性以及持續供電時間發生連續性改變[15]。本節模型采用經典的惠普憶阻器模型，其阻值M（t）的計算式為[16]

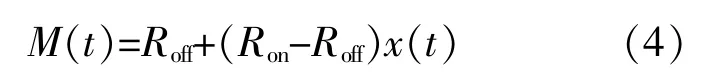
式 中：x（t）為 憶 阻 器 的 狀 態 變 量；Ron，Roff分 別 為 憶阻器的極小憶阻值和極大憶阻值，Ω；t為時間，s。

x（t）的 計 算 式 為

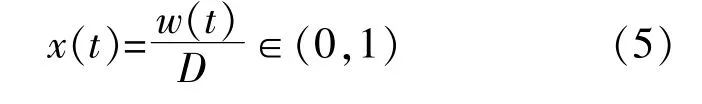
式 中：w（t）為 憶 阻 器 摻 雜 層 的 長 度，m；D為 憶 阻 器的總長度，約為10 nm。

當t=0時，令憶阻器初始阻值為M0。憶阻器的狀態變量動態方程表達式為

式 中：μv為 平 均 離 子 遷 移 率，m2/（s·V）；η為 憶 阻器 極 性；i（t）為 流 經 憶 阻 器 的 電 流，A；f（x）為 窗 函數 [16]。

f（x）的表達式為

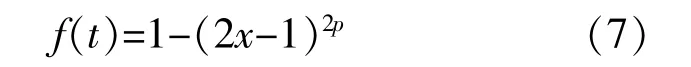
式中：p為窗函數的可控參數，p∈N+。

1.2.2憶阻光伏電池模型

本文提出的兩類憶阻光伏電池模型運用了元件替換的方法。利用憶阻器分別替換光伏電池實際模型中的二極管和旁路電阻Rp。其中，利用憶阻器替換二極管后，得到I類憶阻光伏電池模型；利用憶阻器替換旁路電阻后，得到II類憶阻光伏電池模型。兩類憶阻光伏電池的電路結構如圖2所 示。圖 中：I1，I2分 別 為I，II類 憶 阻 光 伏 電 池 模 型中流經串聯電阻Rs的電流，A。

圖2 憶阻光伏電池的電路結構Fig.2 The circuit configuration of memristive photovoltaic cell

基于式（3）得到I類憶阻光伏電池模型的伏安特性方程為

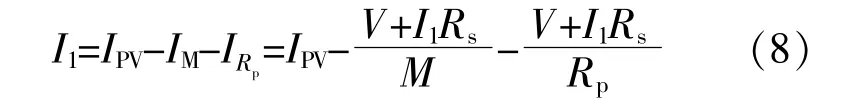
式中：IM為流經憶阻器的電流，A；M為憶阻器的阻 值，Ω。

同理，基于式（3）得到II類憶阻光伏電池模型的伏安特性方程為

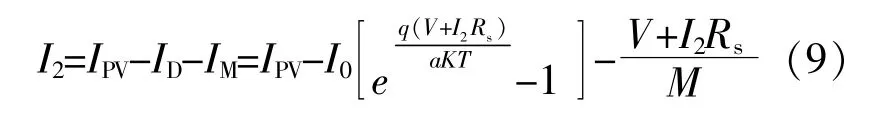
光伏電池等效電路模型中光生電流IPV以及反向飽和電流I0的計算式分別為[2]

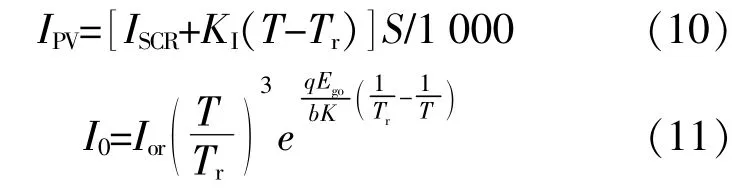
式中：ISCR為某一溫度、太陽輻射強度下的短路電流，A；KI為短路電流溫度系數；Tr為光伏電池參考 溫 度，K；S為 太 陽 輻 射 強 度，W/m2；Ior為 參 考 溫度下指定反向飽和電流，A；Ego為半導體材料跨越能帶間隙時所需的能量，eV；b為曲線擬合系數。

1.3 模型實現及分析

圖3 不同光伏電池模型的仿真結果Fig.3 Experimental results of different photovoltaic cells

本文基于Matlab軟件平臺進行了一系列的對比仿真實驗（定量分析實驗），具體參數：極小憶阻值Ron=100Ω；極大憶阻值Roff=20 000Ω；憶阻器初始阻值M0=10 000Ω；平均離子遷移率 μv=10-14m2/（s·V）；短 路 電 流ISCR=2.52 A；光 伏 電 池 參 考 溫度Tr=300 K；半導體材料跨越能帶間隙時所需的能量Ego=1.35 eV；P-N結的理想因子a=1.6；曲線擬合系數b=1.6；短路電流溫度系數KI=0.001 7 mA/K；參考溫度下指定的反向飽和電流Ior=0.228 7×10-6A；串聯電阻Rs=0.09Ω。其中，憶阻器的器件參 數（Ron，Roff，D，μv）主 要 取 決 于 憶 阻 器 的 制 作 工藝，且這些參數的設定值廣泛應用于眾多相關文獻中[14]～[18]。其余光伏電池參數的提取主要通過擬合某一類真實光伏電池的V-I特性曲線得到。

圖3中分別為通過仿真得到的5類光伏電池模型（理想模型、實際模型、簡化模型、I，II類憶阻光伏電池模型）的伏安特性、伏瓦特性、二極管支路伏安特性，以及兩類憶阻光伏電池模型的憶阻值隨時間的變化曲線。

由 圖3（a），（b）可 知，兩 類 憶 阻 光 伏 電 池 模 型的伏安、伏瓦特性曲線的形態以及變化趨勢與3類經典模型（理想模型、實際模型和簡化模型）基本一致。由圖3（a）可知，II類憶阻光伏電池模型的伏安特性曲線存在一個近似線性下降的區域[l4]，這是由該模型中憶阻器阻值的極速降低導致 的[圖3（d）]。由 圖3（c）可 知，當 非 線 性 憶 阻 元 件替代二極管（I類憶阻光伏電池模型）時，對應支路的伏安特性曲線與傳統光伏電池模型相似，這說明憶阻元件可以替換非線性電路中的二極管。由圖3（d）可知，相同憶阻器在電路中的位置不同時，會導致其所處的激勵環境發生變化，從而導致憶阻器阻值的變化速率隨之改變。

2 憶阻光伏電池模型參數分析

光伏電池模型的主要參數包括外界環境參數和內部器件參數兩部分。外界環境參數主要包含環境溫度T和太陽輻射強度S[1]～[3]；內部器件參數與電路模型的拓撲結構緊密相關。本文中5類光伏電池模型（理想模型、實際模型、簡化模型、I，II類憶阻光伏電池模型）的外部參數均為環境溫度T和太陽輻射強度S；對于內部參數，由于本文提出的兩類憶阻光伏電池模型電路系統的多元化，內部參數的數量相比于經典的光伏電池模型有所增加，其中，I類憶阻光伏電池模型的內部參數包括光生電流IPV、反向飽和電流I0、串聯電阻Rs、旁路電阻Rp、憶阻器總長度D、憶阻器橫截面積SA、憶阻器初始阻值M0、憶阻器極性 η；II類憶阻光伏電池模型的內部參數在上述參數的基礎上，增加了P-N結理想因子a、曲線擬合系數b、參考溫度下的反向飽和電流Ior和跨越能帶間隙時所需的能量Ego。由于憶阻器長度D和橫截面積SA的偏差主要發生在憶阻器的制作工藝過程中，因此，可以將這兩個參數統稱為憶阻器的工藝參數。憶阻器長度D和憶阻器橫截面積SA是由精密儀器測得的，測量完畢后，數值不會再發生改變；憶阻器初始阻值M0和憶阻器極性 η是由憶阻器的初始狀態以及憶阻器在電路中的連接方式決定的。

2.1 外部參數對憶阻光伏電池的影響

本文假設太陽輻射強度和環境溫度不會對憶阻器的特性產生影響。設定環境溫度變化量為ΔT，太陽輻射強度變化量為 ΔS。基于式（10），（11）得到，外部參數改變后的實時光生電流和電池反向飽和電流的計算式分別為

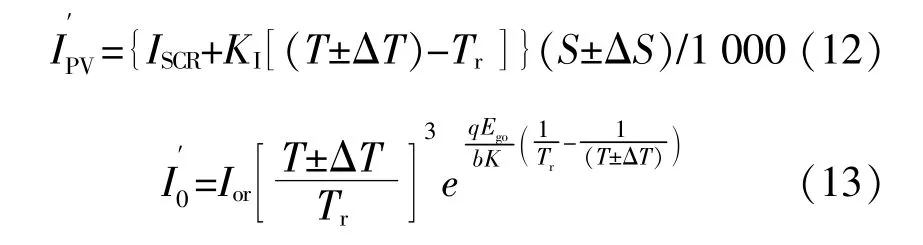
結 合 式（8），（9），保 持 太 陽 輻 射 強 度（或 環 境溫度）不變，當環境溫度（或太陽輻射強度）增大時，兩類憶阻光伏電池模型中的實時光生電流均隨之增大。憶阻光伏電池的反向飽和電流表達式較為復雜，基于該式難以判斷電流的變化趨勢。因此，本文通過Matlab數值仿真結果進一步討論外部參數可能造成的影響，設定太陽輻射強度S集合 為{600，800，1 000，1 200 W/m2}，環 境 溫 度T集合 為{15，30，45，60℃}。

本文采用控制變量法 （當研究太陽輻射強度對憶阻光伏電池模型的影響時，保持環境溫度T為25℃；當研究環境溫度對憶阻光伏電池模型的影響時，保持太陽輻射強度S為1 000 W/m2）研究外部參數對憶阻光伏電池模型的影響。研究結果如圖4所示。

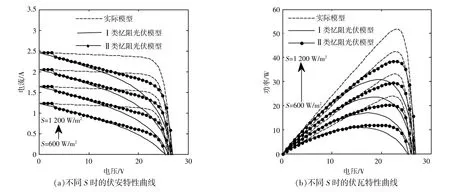
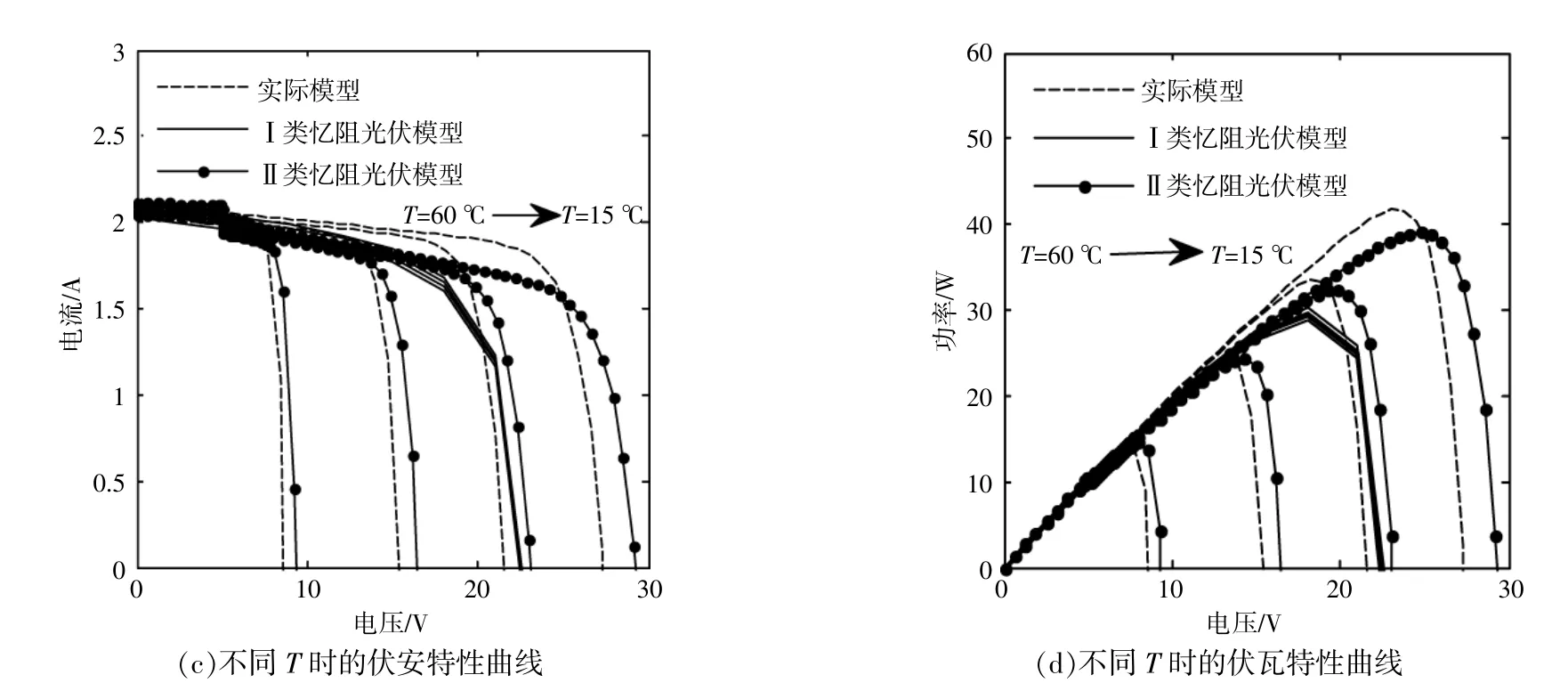
圖4 外部參數對憶阻光伏電池模型的影響Fig.4 Effect of external parameters on memristive model of photovoltaic cells

由 圖4（a），（b）可 知，隨 著 太 陽 輻 射 強 度 的 變化，兩類憶阻光伏電池模型的輸出特性和實際模型的輸出特性的變化規律保持一致。由圖4（c），（d）可知，隨著環境溫度逐漸升高，光伏電池的開路電壓（輸出功率）均逐漸減小，且與I類憶阻光伏電池模型相比，II類憶阻光伏電池模型的輸出特性對環境溫度的變化更為敏感，更接近實際模型。

2.2 內部參數對憶阻光伏電池的影響

本文選擇憶阻器的工藝參數作為研究對象，分別討論各參數對兩類憶阻光伏電池模型輸出特性的影響。假設太陽輻射強度S為1 000 W/m2，環境溫度T為25℃。

2.2.1工藝參數對憶阻光伏電池的影響

與一般的阻抗元件類似，憶阻器的阻抗特性受到自身長度、橫截面積和電導率的影響。基于憶阻器的物理模型、電阻定律和式（4）得到，當憶阻器長度和橫截面積分別存在偏差時，該憶阻器的 實 際 憶 阻 值M′（x，D），M′（x，SA）分 別 為[17]

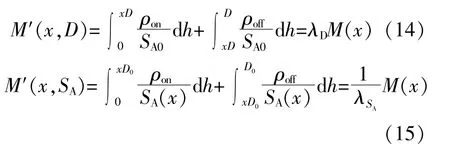
式中：ρon，ρoff分別為憶阻器摻雜區域和非摻雜區域的電阻率；D0，SA0分別為理想狀態下，憶阻器的長度和橫截面積；λD為長度偏差因子；λSA為橫截面積偏差因子。

λD，λSA的 計 算 式 分 別 為

基 于 式（8），（9），當 憶 阻 器 長 度 存 在 偏 差 時，兩類憶阻光伏電池的伏安特性方程分別為

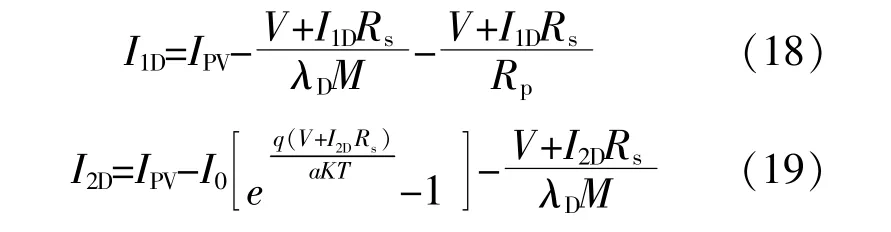
式 中：I1D，I2D分 別 為 憶 阻 器 長 度 存 在 偏 差 時，I，II類憶阻光伏電池模型中流經串聯電阻Rs的電流。

同理，當憶阻器橫截面積存在偏差時，基于式（14），（15）得 到，兩 類 憶 阻 光 伏 電 池 的 伏 安 特 性 方程分別為

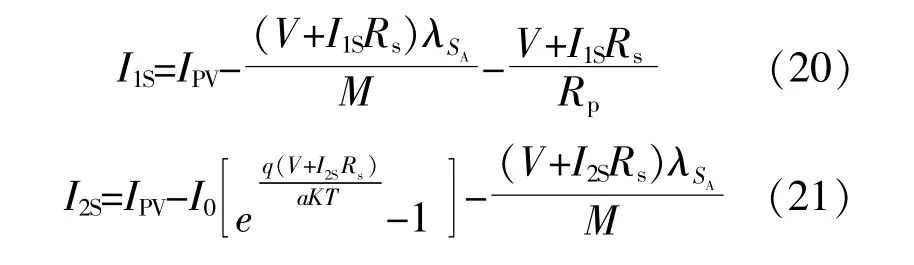
式中：I1S，I2S分別為憶阻器橫截面積存在偏差時，I，II類憶阻光伏電池模型中流經串聯電阻Rs的電流。

本文通過Matlab軟件模擬了當工藝參數偏差不同時，憶阻器和憶阻光伏電池的電氣特性。橫截面偏差和長度偏差對憶阻值的影響見圖5。

由圖5可知，當憶阻器的橫截面積或長度存在偏差時，憶阻器的阻值也隨之發生變化（與理想情況下阻值不同）。即當憶阻器存在橫截面偏差且偏差因子 λSA＜1時，該憶阻器的阻值大于理想狀態下的阻值；同樣地，當憶阻器存在長度偏差且偏差因子 λD＞1時，該憶阻器的阻值也會大于理想狀態下的阻值。

圖5 橫截面偏差和長度偏差對憶阻值的影響Fig.5 Effect of cross section and length variation on memristances

本文運用了蒙特卡洛算法[14]研究憶阻器的長度對兩類憶阻光伏電池模型伏安特性的影響。圖6為當憶阻器長度偏差為0.5時，兩類憶阻光伏電池的伏安特性隨憶阻器長度的變化情況。

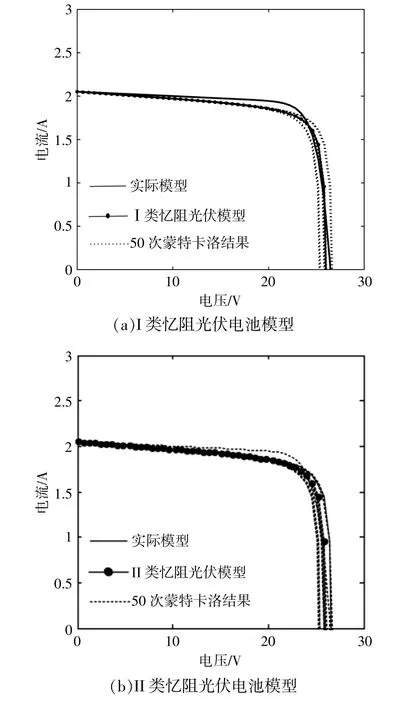
圖6 當憶阻器長度偏差為0.5時兩類憶阻光伏電池的伏安特性隨憶阻器長度的變化情況Fig.6 Volt-ampere characteristics of two memristive photovoltaic cells when the length variation of memristor is 0.5

由圖6可知，當憶阻器長度不存在偏差時，I，II類憶阻光伏電池模型的伏安特性曲線與實際模型的伏安特性曲線十分接近，但是尚未完全擬合；當憶阻器長度偏差為0.5，且算法運行50次時，發現兩類憶阻光伏電池模型的動態伏安特性曲線均處于實際模型動態伏安特性曲線的兩側，且隨著偏差的增大，能夠進一步實現對實際模型動態伏安特性曲線的完全覆蓋，這說明本文提出的兩類憶阻光伏電池模型具有與實際電池模型相似的電氣特性。

當憶阻器橫截面偏差不同時，兩種憶阻光伏電池的伏安特性如圖7所示。

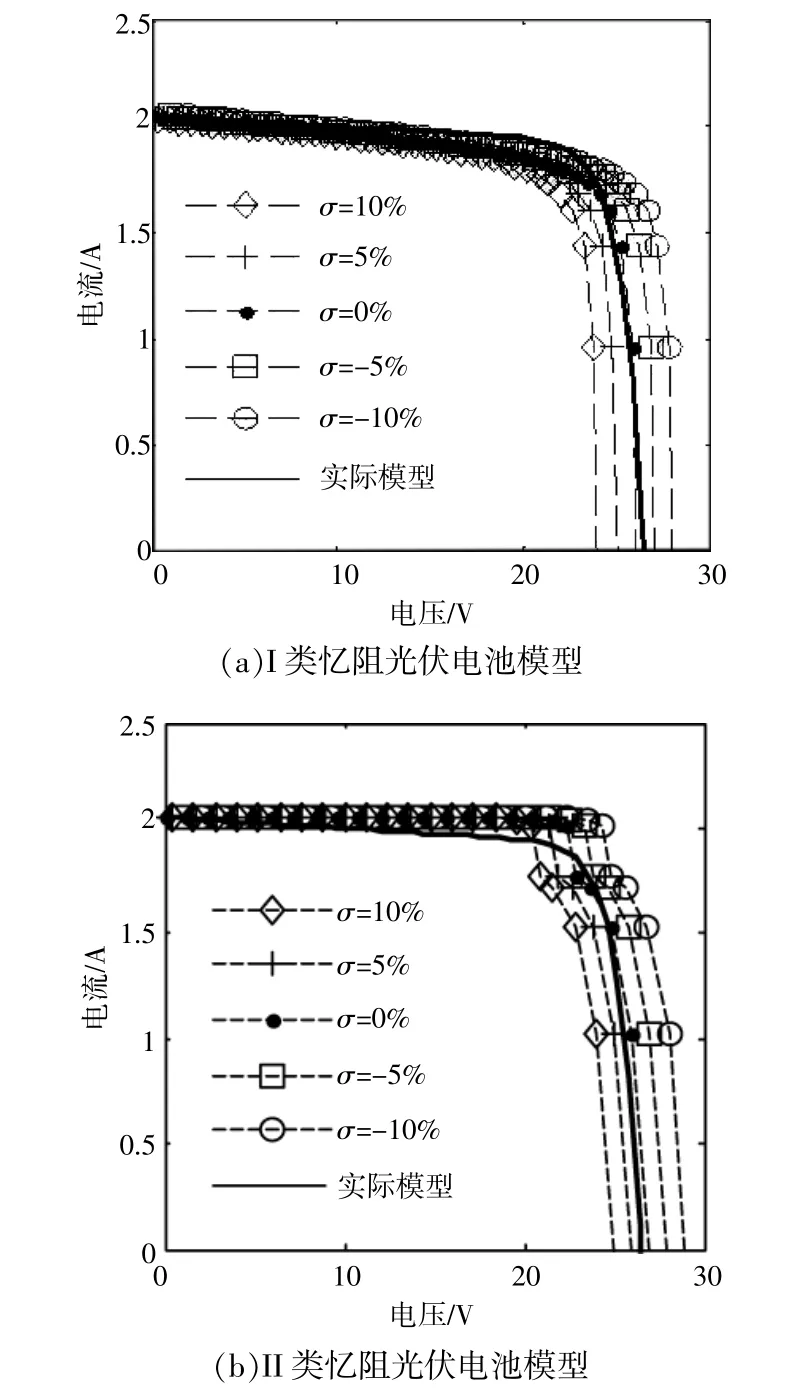
圖7 當憶阻器橫截面偏差不同時，兩類憶阻光伏電池的伏安特性Fig.7 Volt-ampere characteristics of two memristive photovoltaic cells under different cross section variances

由圖7可知，當憶阻器的橫截面不存在偏差時（偏差 σ=0），兩類憶阻光伏電池的伏安特性曲線與實際模型的伏安特性曲線十分接近，但是尚未完全擬合。改變憶阻器的橫截面偏差，研究不同偏差情況下，兩類憶阻光伏電池的伏安特性。當憶阻器橫截面偏差σ分別為-10%，-5%，5%和10%時，兩類憶阻光伏電池的伏安特性曲線分布在實際模型的伏安特性曲線兩側，說明憶阻器橫截面的偏差能夠使得憶阻光伏電池模型與實際模型的伏安特性存在完全擬合的可能性。當偏差σ為正值時（5%，10%），兩類憶阻光伏電池的開路電壓均減少，表明增大憶阻器橫截面積能夠減小光伏電池的開路電壓；反之，當偏差 σ為負值時（-10%，-5%），兩類憶阻光伏電池的開路電壓均增加，表明減小憶阻器橫截面積能夠增大光伏電池的開路電壓。

2.2.2憶阻器初始阻值對憶阻光伏電池的影響

設定憶阻器初始阻值M0分別為13.615，10.435，7.255，4.075 kΩ，研 究 憶 阻 器 初 始 阻 值 對憶阻光伏電池輸出特性的影響。圖8，9均為仿真結果。

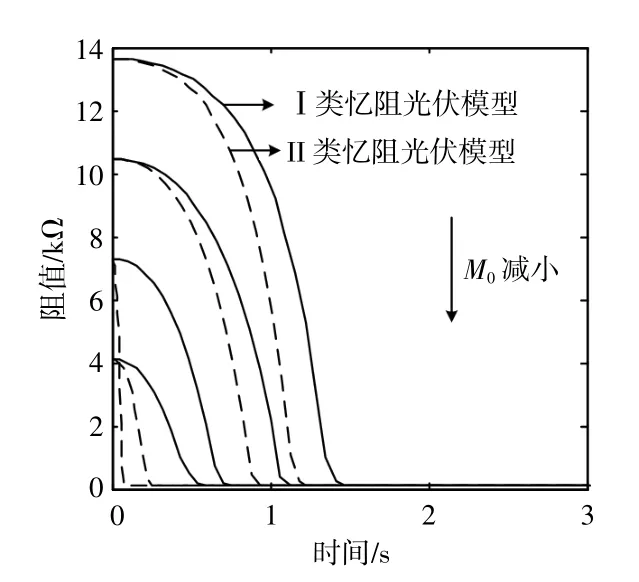
圖8 當憶阻器初始阻值不同時，兩類憶阻光伏電池模型中憶阻值隨時間的變化曲線Fig.8 Memristance-time variation curves of two memristive photovoltaic cells under different initial memristor values

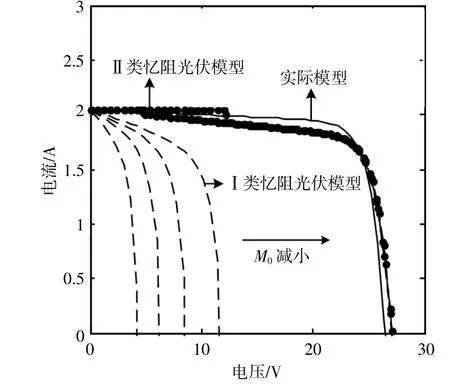
圖9 當憶阻器初始阻值不同時，兩類憶阻光伏電池模型的伏安特性Fig.9 Volt-ampere characteristics of two memristive photovoltaic cells under different initial memristor values

由圖8可知，當憶阻器以正極性接入兩類憶阻光伏電池模型中時，憶阻器的阻值將隨著時間的增加逐漸減小，最終收斂于極小憶阻值；反之，當憶阻器以負極性接入兩類憶阻光伏電池模型中時，根據憶阻器自身的阻值變化特點，可以合理地推測出：憶阻器的阻值將隨著時間的增加逐漸增大，最終收斂于極大憶阻值。

由圖9可知，相比于II類憶阻光伏電池模型，I類憶阻光伏電池模型的伏安特性與光伏電池實際模型的伏安特性更為接近。特別地，隨著憶阻器初始阻值的增加，I類憶阻光伏電池模型的開路電壓逐漸增加，而II類憶阻光伏電池模型的開路電壓受到憶阻器初始阻值的影響較小，幾乎不發生改變。

2.2.3極性參數對憶阻光伏電池的影響

憶阻器作為一種具有極性的二端電路元器件，當輸入激勵方向固定時，極性參數會影響憶阻值的變化方向[17]，從而間接影響憶阻光伏電池的電氣特性。

圖10為當憶阻器極性參數不同時，兩類憶阻光伏電池模型中憶阻值隨時間的變化曲線。

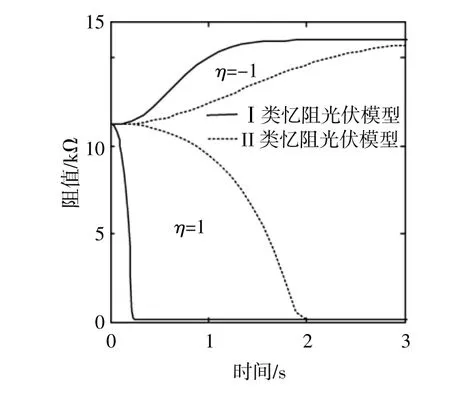
圖10 當憶阻器極性參數不同時，兩類憶阻光伏電池模型中憶阻值隨時間的變化曲線Fig.10 Memristance-time variation curves of two memristive photovoltaic cells under different memristor polarity parameters

由圖10可知：當憶阻器以負極性接入兩類憶阻光伏電池模型中時（即η=-1），憶阻值均呈現逐漸增大的變化趨勢；反之，當憶阻器以正極性接入兩類憶阻光伏電池模型中時（即η=+1），憶阻值的變化則呈現完全相反的趨勢，即逐漸減小，最終收斂于極小憶阻值。

圖11為當憶阻器極性參數不同時兩類憶阻光伏電池模型的伏安特性

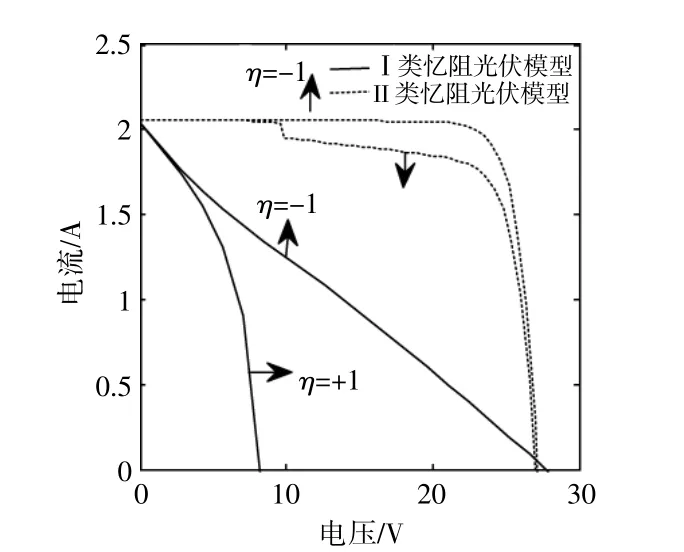
圖11 當憶阻器極性參數不同時，兩類憶阻光伏電池模型的伏安特性Fig.11 Volt-ampere characteristics of two memristive photovoltaic cells under different memristor polarity parameters

由圖11可知，極性參數的變化更容易影響I類憶阻光伏電池模型的開路電壓值。當憶阻器以負極性接入I類憶阻光伏電池模型時（η=-1），得到開路電壓約為28.3 V；反之，當憶阻器以正極性接入I類憶阻光伏電池模型中時（η=1），得到的開路電壓約為9.1 V。相比于I類憶阻光伏電池模型，極性參數的變化對II類憶阻光伏電池模型的開路電壓影響較小。當極性參數發生變化時，II類憶阻光伏電池模型的開路電壓均約為27.1 V。基于此，憶阻器作為一種納米級電路元器件，當其與光伏電池模型結合時，若對應的等效電路制備完成，則其內部參數長度D、橫截面積SA以及極性參數 η均不會發生改變。此時，通過不斷地修正電路模型中憶阻器的初始值M0，使提出的兩類憶阻光伏電池模型與傳統光伏電池的V-I曲線盡可能重合，從而增加兩類憶阻光伏電池模型的準確性和普適性。

本文通過修正初始阻值M0，得到5種不同的光伏電池模型之間的伏安特性絕對誤差，如表1所示。

表1 5種不同光伏電池模型伏安特性的絕對誤差Table 1 Absolute error of volt-ampere characteristics of five different photovoltaic cells %

為了使本文提出的I，II類憶阻光伏電池模型和其他3類電池模型的伏安特性計算誤差均盡可能小，本文選擇了較理想的憶阻器初始阻值：I類憶阻光伏電池模型的初始阻值M0設為15.75 kΩ；II類憶阻光伏電池模型的初始阻值M0為5.27 kΩ。

3 結論

針對傳統光伏電池仿真模型存在的自適應性差、普適性弱的問題，本文基于光伏電池基本電路模型，分別運用非線性憶阻器代替光伏電池基本電路模型中的二極管和并聯電阻，建立了兩類憶阻光伏電池模型，并利用數值仿真結果驗證了這兩類憶阻光伏電池模型的有效性，得到如下分析結果。

①當外部參數發生變化時，提出的兩類憶阻光伏電池模型的輸出特性和實際模型的輸出特性的變化規律保持一致。

②本文提出的兩類憶阻光伏電池模型具有與實際電池模型相似的電氣特性。