基于變密度法的平模臺振加強筋布局優化

蔡安江，楊奇琦

(西安建筑科技大學 機電工程學院，西安 710055)

1 引 言

平模臺振因生產效率高且生產預制構件種類多而成為裝配式建筑生產線的重要設備，但是普遍存在振動臺面剛度不足和振動能量利用率較低等問題，導致振動效果不理想，混凝土預制構件成型質量差。為了解決上述問題，振動臺面常采用加強筋結構，既能為平模臺振各部件提供安裝位置，又能提高振動臺面剛度，改善振動臺面動力學傳遞特性[1,2]，使設備運行平穩、噪聲降低、能量利用率提高，從而提升平模臺振的振動效果和混凝土預制構件成型質量。因此，研究振動臺面加強筋布局優化對于提高平模臺振的振動效果具有重要意義。

隨著拓撲優化技術的不斷成熟，國內外學者關于加筋板殼結構的優化進行了大量研究工作。Tamijani等[3]采用伽遼金法對加筋板結構進行了分析，建立了Kriging代理模型，并利用遺傳算法優化加筋板結構的尺寸和形狀，結果表明，采用無網格法可在保持板的幾何形狀和網格尺寸不變的情況下對每個設計點重新生成加強筋，大幅度縮短了計算時間。Xiang等[4]采用仿生設計方法對加筋工作臺的結構進行拓撲優化，與傳統設計相比，優化后的仿生結構變形量和重量減小，固有頻率提高，工作臺力學性能明顯提升。Li等[5]研究了薄板結構在簡諧激振力作用下的加強筋布置問題，利用植物葉脈的自適應生長機制，提出一種以指定位置的位移響應幅值最小為目標的進化算法，實現了連續體結構的剛度優化設計。崔榮華等[6]研究了不同邊界條件下薄板的加強筋分布優化，根據加筋板結構各部分抗彎剛度的差異，建立等效剛度模型，基于水平集法得到了加強筋的最優分布。劉海等[7]基于變密度法進行加強筋布局優化來實現加筋箱體結構降噪設計，利用移動漸近線(MMA)尋優算法確定了加強筋的位置，取得了良好的降噪效果。李蕾等[8]提出了平板加強筋生長設計方法，利用單元靈敏度決定結構中加強筋的保留或去除，獲得了多種邊界條件下平板加強筋的最優布局。

振動臺面結構設計時，臺面的剛度和強度等力學性必須滿足預制構件最佳成型質量的需求，并且要考慮各組成部件安裝位置的合理性，以使平模臺振達到理想的振動效果。振動臺面結構設計不合理將無法生產滿足強度要求的預制構件，因此振動臺面的優化設計非常必要。目前，振動臺面結構單一且存在很多局限性，其設計大多依賴工程人員的主觀經驗，缺乏類似的振動臺面優化設計工作。本文以提升平模臺振設備的振動效果為目標，基于變密度法對振動臺面加強筋的布局進行了拓撲優化。

2 優化問題分析

平模臺振系統模型如圖1所示，系統主要由振動臺面、底座和激振器組成。振動臺面由矩形鋼板和加強筋兩部分焊接而成，并有12個橡膠彈簧支撐，振動臺面兩側共安裝8個激振器提供激振力，激振力通過側板傳遞到臺面，再由臺面傳遞給混凝土預制構件，為預制構件提供振動能量并完成密實成型。

圖1 平模臺振系統模型

平模臺振力學模型如圖2所示，激振器對稱分布在振動臺面兩側，偏心塊做同步反向旋轉運動產生離心慣性力，慣性力沿x方向分力相互抵消，沿z方向分力疊加形成激振力，驅動振動臺面沿z方向作簡諧振動。

振動臺面總激振力為

(1)

式中Fr(x,y,t)為第r個激振器提供的激振力,m0為偏心塊質量,ω為偏心塊角速度,t為時間。

平模臺振工作狀態是動態非線性的，振動臺面承受的載荷也具有復雜的非線性[9]，而拓撲優化方法難以對動態非線性過程建立準確的數學模型。考慮到若振動臺面在最大載荷工況下能滿足平模臺振的工作需求，則在其他工況下也能滿足工作需求。所以，進行拓撲優化時選取載荷最大的工況進行分析，即振動臺面所受激振力最大。在此工況下，每個激振點處的激振力幅值為18 kN，且需約束振動臺面沿x和y方向的移動自由度及z方向的轉動自由度，振動臺面底部支承點處施加彈簧約束模擬橡膠彈簧底座。

目前，振動臺面加強筋大多采用如圖3所示的布局，加強筋等間距并排布置在臺面底部。其優點在于加強筋的布置形式簡單，簡化了振動臺面的設計及制造，并且載荷能夠均勻分配到每個加強筋。這種振動臺面以總質量最小為設計目標，以加強筋間距為設計變量，加強筋數量與振動臺面總質量的關系如圖4所示。可以看出，隨著加強筋數量的增加，振動臺面總質量逐漸減小，直至矩形鋼板達到最小厚度。即存在最優的加強筋數量，使得振動臺面實現輕量化設計目標。雖然此振動臺面結構已用于實際生產，但是其存在一定的局限性，如振動臺面整體剛度不足和振動能量傳遞效率低等。

圖2 平模臺振力學模型

3 振動臺面的優化設計

3.1 拓撲優化數學模型

拓撲優化的基本思想是在給定載荷及邊界條件下，在設計空間中尋找材料最優分布形式[10-12]。與傳統優化設計不同的是，拓撲優化只需給出結構參數(材料特性、載荷和邊界條件)和材料去除體積比[13-15]。

本文優化問題實際上是材料分布狀態0～1優化問題，即確定振動臺面基結構材料的有(表示為1)與無(表示為0)，最終生成加強筋布局的設計方案。采用基于SIMP材料插值模型的拓撲優化方法[16]，得到具有可變剛度的各向同性材料，將材料相對體積密度x(x在0～1之間連續變化)作為設計變量分配給設計空間的每個有限單元，該密度可直接影響單元剛度矩陣。為了消除沒有物理意義的中間密度，在設計變量中加入懲罰因子，迫使設計變量趨向于極值0或1，以生成更離散的結構。

圖3 振動臺面加強筋的布局

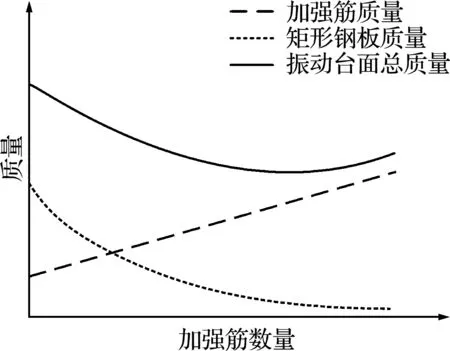
圖4 加強筋數量與振動臺面總質量的關系

SIMP材料插值模型如下：

(2)

式中Ke為e號單元優化后剛度矩陣，K0為e號單元初始剛度矩陣，xe為e號單元的相對密度，p為中間密度懲罰因子，取p=3。xe的取值區間為[0,1]，當xe取0時表示該單元材料缺失，當xe取1時表示該單元充滿材料。為了避免剛度矩陣的奇異性，通常將單元相對密度下限xmin限制為很小的值。

以振動臺面結構的剛度最大即柔度最小為優化目標，以單元相對密度作為設計變量，以體積分數為約束條件，建立拓撲優化數學模型如下：

(3)

式中x為單元相對密度向量，C為結構總體柔度，F為結構載荷向量，U為結構位移向量，K為結構總體剛度矩陣，V為結構優化后體積，f為保留體積比，V0為結構設計域體積，ve為e號單元的體積，xmin為單元密度下限，取xmin=0.001，xmax為單元密度上限。

對拓撲優化問題進行靈敏度分析，將目標函數相對于設計變量求導為

(4)

利用伴隨方法[17]，可得到以下結果

(5)

將SIMP材料插值模型引入到式(5)，得到結構總柔度相對設計變量的靈敏度為

(6)

式中Ue為單元位移向量。

獲得靈敏度結果后，在求解優化模型時采用最優準則法，基于KKT(Karush Kuhn Tucker)條件得到拓撲優化模型(3)最優性條件表示為

(e=1，2，…，n)(7)

式中λ為拉格朗日乘子。本文載荷為設計獨立載荷，?C/?xe<0。式(7)可改寫為

(e=1，2，…，n)(8)

為了控制移動步長和確保迭代穩定，引入步長因子ξ和阻尼因子δ，ξ和δ在區間[0,1]內取值。由此可構造設計變量的迭代公式為

(9)

i為迭代步數。

根據KKT條件可知，最優解處的約束轉化為等式約束，將迭代公式代入取等號的體積約束中，可獲得關于λ的非線性代數方程，使用二分法便可得到拉格朗日乘子λ。

3.2 拓撲優化有限元模型的建立

有限元軟件ANSYS Workbench的Topology Optimization拓撲優化模塊使用的技術是基于變密度方法的，利用該模塊進行拓撲優化的流程為,定義材料屬性，導入幾何模型；劃分基結構網格，施加約束及載荷；設置拓撲優化參數，計算求解。

在結構拓撲優化之前，首先需要確定設計空間及非設計空間。如圖5所示，設計空間為加強筋分布區域，此空間的材料需要部分去除；而非設計空間則是矩形鋼板區域，此空間結構特征保持不變。加強筋分布區域厚度為200 mm，矩形鋼板區域厚度為10 mm，拓撲優化過程中需要從厚度為210 mm的基結構中去除設計空間的多余材料，生成加強筋材料的分布形式。

圖5 振動臺面設計空間及非設計空間

振動臺面基結構有限元模型如圖6所示，臺面和加強筋材料均為Q235，主要材料參數為,彈性模量E=2×1011Pa，泊松比ν=0.3，密度ρ=7850 kg/m3。采用六面體單元對基結構進行網格劃分，網格劃分過程中沿基結構厚度方向劃分較為密集，劃分為4層網格。基結構有限元模型共72376個單元，293738個節點。

3.3 體積分數的影響

體積分數(VF)是拓撲優化的重要參數，在某些情況下可直接通過最終設計質量確定體積分數。本文振動臺面原結構中加強筋質量(2692 kg)與設計空間質量(56112 kg)相比非常小，導致體積分數小于5%。Rozvany[18]指出過低的體積分數不能用于密度拓撲優化，通常采用較高的體積分數。此外，設計空間的體積分數響應不能直接代表最終設計，因為沒有考慮到應用不同截面加強筋來實現同樣的功能，同時加強筋的結構特點也會導致體積分數非常小。

選取體積分數在5%～30%之間的拓撲優化結果進行對比分析，如圖7所示。圖中黑色為需要刪除材料的區域，相對密度接近0；灰色為需要保留材料的區域，相對密度接近1。通過比較不同體積分數的拓撲優化結果可以確定振動臺面最佳傳力路徑，指導加強筋的重新布局，最終生成可行的設計方案。可以看出，在臺面寬度方向上需要分布若干加強筋；但是對于不同的體積分數，臺面長度方向上材料分布有所差異，低體積分數不像高體積分數材料分布清晰穩定，這是體積分數過低導致的。此外，所有拓撲優化結果為對稱形狀，原因是拓撲優化設計中存在對稱性約束，即結構對稱面上指向邊界的位移自由度和繞邊界的轉動自由度受到約束。加強筋在尺寸調整和位置確定之前，其真實性能仍是未知的，因此進行加強筋布局的優化研究時，體積分數是一個需要研究的重要參數。

圖6 振動臺面基結構有限元模型

圖7 不同體積分數的拓撲優化結果

3.4 振動臺面的結構設計

依據拓撲優化結果能夠確定加強筋位置，但不能確定加強筋具體的尺寸參數和截面形狀，故直接使用矩形梁單元代替材料分布區域是不正確的。通過查看拓撲優化結果，材料分布區域的截面形狀與工字鋼的截面形狀較為吻合，且工字鋼具有質量小、剛度大等優點，因此選取不同型號的工字鋼作為振動臺面的加強筋。

振動臺面加強筋布局設計方案如圖8所示，綜合考慮振動臺面的強度、剛度及制造成本，在制定設計方案時選取體積分數為30%。根據拓撲優化結果，在材料保留區域設置工字鋼生成新的設計方案，并通過有限元軟件測試，進一步提升振動臺面的力學性能。此外，為了便于振動臺面的制造以及滿足批量生產的需要，在符合結構優化結果的基礎上將加強筋設計為規則的軸對稱布局。

圖8 加強筋布局設計方案

設計方案中，工字鋼A的腹板處用來安裝激振器，工字鋼B和C的作用為組成模臺框架，增大臺面剛度和防止振動臺面發生撓曲。考慮到振動臺面縱向尺寸較大，將其長度方向上的加強筋由原結構的單工字鋼增加為雙工字鋼共同承受負載。振動臺面寬度方向上，加強筋由原結構的等距分布改變為需要加強部位的非等距分布。二次加強筋1和2用來連接主要加強筋，加固振動臺面邊緣以及傳遞激振能量。工字鋼B的型號為25b，其余工字鋼型號均為20a。

優化后振動臺面模型如圖9所示，振動臺面總質量由原來的5878 kg變為5555 kg，減重323 kg，實現了結構輕量化設計。

圖9 優化后振動臺面模型

4 振動臺面的性能評估

利用有限元軟件對優化后的結構進行模態分析和諧響應分析，測試振動臺面力學性能及平模臺振振動效果。

4.1 模態分析

通過ANSYS Workbench的Modal模塊，計算得到振動臺面前8階振型如圖10所示，振動臺面前10階固有頻率列入表1。為了方便對比，將原結構和優化結構的前10階固有頻率一并列入 表1。可以看出，優化后振動臺面的固有頻率明顯提高，增幅在4.46%～32.71%。

圖10 優化后振動臺面前8階振型

4.2 諧響應分析

在實際工況中，平模臺振長時間處于周期振動狀態下工作，進行諧響應分析能真實地反映振動臺面在工作中的力學性能。通過求解計算，得到優化前后振動臺面在工作頻率50 Hz時的應力分布云圖及位移云圖如圖11和圖12所示。

圖11 振動臺面應力分布云圖

圖12 振動臺面位移云圖

對比發現，振動臺面強度提高，原結構的最大應力為 14.51 M Pa，優化結構的最大應力為 6.998 M Pa，比優化前降低了51.77%；振動臺面整體剛度提高，原結構的最大位移量為0.598 mm，優化結構的最大位移量為0.555 mm。而且優化前最大變形出現在振動臺面中部，對預制構件的成型質量會產生較大影響，優化后最大變形在振動臺面短邊邊緣處，可通過焊接角鋼的方法避免變形出現。

綜上所述，優化后振動臺面的各階固有頻率避開了工作頻率50 Hz，有效避免了共振發生，防止了平模臺振設備損壞；優化后振動臺面可顯著提高強度和剛度，從而提高了平模臺振設備的振動效果。

5 結 論

(1) 振動臺面作為平模臺振設備的關鍵部件，在工作中反復承受高頻簡諧載荷，其加強筋布局對平模臺振振動效果及混凝土預制構件成型質量有著重要影響。

(2) 提出了利用變密度拓撲優化方法改進平模臺振振動臺面加強筋布局的方法，進行了結構總柔度相對于設計變量的靈敏度分析，采用最優準則法對拓撲優化模型進行求解。根據拓撲優化結果得到優化后的振動臺面，其力學性能顯著提高，并且實現了結構輕量化。

(3) 采用優化后振動臺面的平模臺振可有效提高振動效果，很好滿足了平模臺振的性能要求。驗證了基于變密度法的振動臺面加強筋布局優化的可行性，對工程實際中平模臺振的設計具有一定指導意義。