無額外自由度廣義有限元非線性分析

馬今偉，段慶林，陳嵩濤

(大連理工大學(xué) 工業(yè)裝備結(jié)構(gòu)分析國家重點(diǎn)實(shí)驗(yàn)室，大連 116024)

1 引 言

廣義有限元法[1]能夠方便地引入待求解問題相關(guān)的局部強(qiáng)化函數(shù)，具有計(jì)算精度高、易于程序?qū)崿F(xiàn)(對(duì)已有的有限元程序改動(dòng)較小)等優(yōu)點(diǎn)，引發(fā)了廣泛關(guān)注。該方法一般認(rèn)為源于單位分解法[2]和單位分解有限元法[3]，甚至還可追溯到更早期的研究[4,5]。由于局部強(qiáng)化函數(shù)可以根據(jù)具體問題方便靈活地引入，廣義有限元法已廣泛應(yīng)用于各類問題，如裂紋擴(kuò)展[6]、形狀優(yōu)化[7]、非光滑界面[8]和水力壓裂[9]等。

在廣義有限元法[1]中，局部強(qiáng)化函數(shù)的引入依賴于額外自由度。以本文考慮的靜力問題為例，每個(gè)計(jì)算節(jié)點(diǎn)除標(biāo)準(zhǔn)的位移自由度之外，還需設(shè)置與局部強(qiáng)化函數(shù)數(shù)目相等的額外自由度。這導(dǎo)致了求解規(guī)模的急劇增大。更為嚴(yán)重的是，依賴額外自由度引入局部強(qiáng)化函數(shù)會(huì)造成線性相關(guān)性問題[3,10,11]，導(dǎo)致剛度陣奇異。針對(duì)該問題，目前已有一些行之有效的方法，如穩(wěn)定廣義有限元方法(SGFEM)[12]以及正交廣義有限元方法(OGFEM)[13]等。這些方法能有效消除線性相關(guān)性問題，但仍然需要使用額外自由度，不能減小求解規(guī)模，實(shí)現(xiàn)起來也與標(biāo)準(zhǔn)有限元法有較大差異。

田榮[14]采取了一種不同的思路，提出不使用額外自由度引入局部強(qiáng)化函數(shù)，建立了無額外自由度廣義有限元法。該方法不僅消除了前述線性相關(guān)問題，而且節(jié)點(diǎn)自由度與標(biāo)準(zhǔn)有限元法相同，同時(shí)仍然保留了廣義有限元方法的諸多優(yōu)勢(shì)，如局部強(qiáng)化函數(shù)仍然能夠方便靈活地引入。基于這一思想，田榮等[15,16]也對(duì)廣泛應(yīng)用于裂紋問題的擴(kuò)展有限元法進(jìn)行了改進(jìn)，建立了iXFEM(improved XFEM)方法。同樣地，無額外自由度廣義有限元法作為對(duì)原GFEM方法的重要改進(jìn)，在本文中簡記為iGFEM。

目前，對(duì)于本文考慮的靜力問題，iGFEM仍然僅限于線彈性小變形分析。本文將基于考慮幾何和物理非線性的計(jì)算方法理論[17-20]，將該方法推廣至彈塑性大變形問題的非線性分析。雖然，有限元法的非線性分析相對(duì)成熟，并已發(fā)展了諸多計(jì)算軟件，包括我國自主軟件SiPESC[21]。但是，低階單元非線性分析的計(jì)算精度往往難以令人滿意。iGFEM 方法可使用低階單元的計(jì)算網(wǎng)格建立高階的插值近似，若能有效改善非線性分析的計(jì)算精度，將具有重要的研究意義和潛在的應(yīng)用價(jià)值。

2 控制方程

參考初始構(gòu)型，靜力平衡方程及邊界條件為

?Pi j/?Xj+bi=0inΩ0

(1)

(2)

Wext-Wint=0

(3)

式中Wint和Wext分別表示內(nèi)力和外力虛功:

(4)

(5)

式中δui為虛位移。弱形式(3)的進(jìn)一步空間離散依賴于位移場(chǎng)的插值近似，這是iGFEM方法的核心內(nèi)容。

3 無額外自由度的廣義有限元近似

廣義有限元方法的位移近似可寫為

(6)

(7)

該式可進(jìn)一步寫為

(8)

式中

(9)

圖1 計(jì)算網(wǎng)格上的節(jié)點(diǎn)片

(10)

其中

(11)

式中ω(x)為MLS的權(quán)函數(shù)，pK=p(xK)，本文取為如下的二次基底

(12)

4 節(jié)點(diǎn)力及其線性化

為得到離散化方程，將iGFEM的位移近似式(8)代入弱形式(3)，并通過位移的獨(dú)立變分可得到

(13)

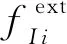
(14)

(15)

式(13)是以位移為基本未知量的非線性方程，需采用Newton-Raphson迭代求解。為此，對(duì)節(jié)點(diǎn)內(nèi)力作如下線性化

(16)

式(16)的推導(dǎo)利用了以下關(guān)系：

(17)

(18)

其中

(19)

(20)

應(yīng)說明的是，本文僅考慮不隨構(gòu)形變化的外載，因而無須對(duì)節(jié)點(diǎn)外力進(jìn)行線性化。

5 本構(gòu)模型

本文考慮的亞彈-塑性材料的彈性本構(gòu)關(guān)系可寫為

(21)

(22)

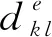
(23)

(24)

式中γ為塑性參數(shù)，rk l為塑性流動(dòng)方向。對(duì)于本文考慮的J2關(guān)聯(lián)塑性有rk l=?f/?σk l，f為屈服面。

(25)

式中q為內(nèi)變量，在本文僅考慮為等效塑性應(yīng)變，‖ξ‖為等效應(yīng)力，K(α)=σY+Hα為后繼屈服強(qiáng)度，σY為初始屈服強(qiáng)度，α為等效塑性應(yīng)變，H為塑性模量。將式(23，24)代入式(21)可得

(26)

(γ≥0，f≤0)(27)

對(duì)于本文考慮的超彈性材料，本構(gòu)模型可由第二PK應(yīng)力Si j和格林應(yīng)變Ek l寫為

(28)

(29)

將上述兩種本構(gòu)模型代入式(18)，則節(jié)點(diǎn)內(nèi)力率可寫為

(30)

(31)

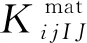
(32)

6 數(shù)值算例

采用三個(gè)算例考察本文發(fā)展的非線性iGFEM 方法處理彈塑性大變形問題的有效性和計(jì)算精度。為作比較，對(duì)標(biāo)準(zhǔn)線性有限元方法也進(jìn)行了數(shù)值實(shí)現(xiàn)，并標(biāo)記為FEM。

6.1 淺拱

如圖2所示，兩端固支弧形淺拱在頂部中心點(diǎn)A處受向下的集中力作用。淺拱中性軸半徑為100 mm，拱厚為2 mm，淺拱對(duì)應(yīng)圓心角為28.06°，材料為超彈性，楊氏模量E=4.8×103N/mm2，泊松比υ=0。iGFEM方法計(jì)算得到的淺拱變形及相應(yīng)的σx x應(yīng)力場(chǎng)如圖3所示。圖4比較了兩種方法的載荷-位移曲線。在相同的計(jì)算網(wǎng)格下，iGFEM 的計(jì)算結(jié)果與解析解吻合，F(xiàn)EM則發(fā)生了明顯的偏離。應(yīng)說明的是，本文FEM僅指標(biāo)準(zhǔn)的線性三角形單元，若采用高階單元或使用精巧的單元技術(shù)，有限元法的計(jì)算精度將會(huì)得到顯著提高。

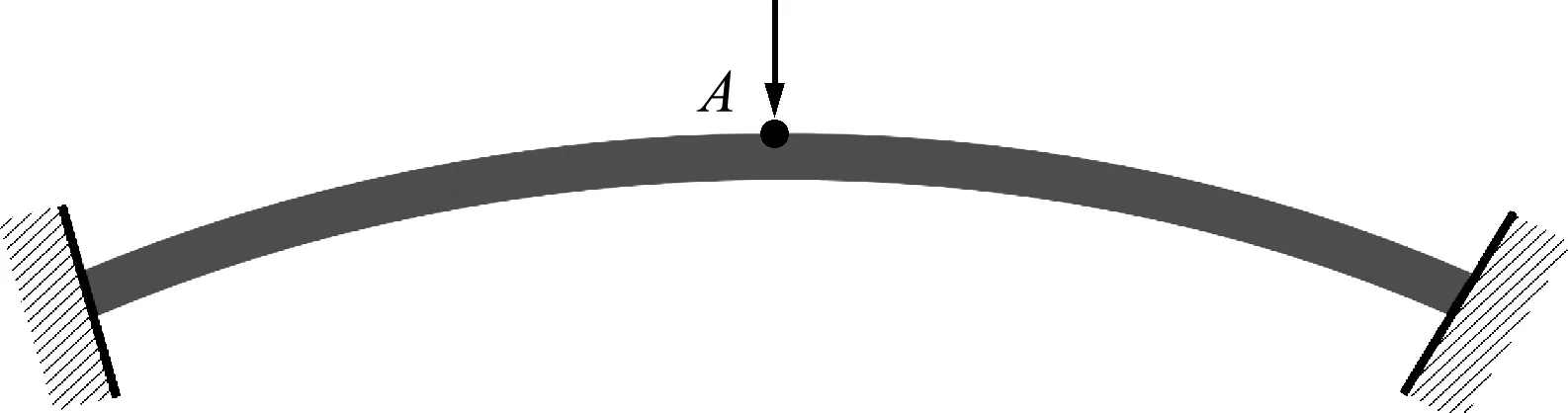
圖2 受集中力作用的淺拱

圖3 淺拱變形及σxx應(yīng)力場(chǎng)

圖4 淺拱A點(diǎn)處的載荷-位移曲線

6.2 懸臂梁

如圖5所示，懸臂梁一端固支，另一端受向上大小為F=10 N的集中力作用，梁長為20 mm，厚度為1 mm，材料為超彈性，楊氏模量E=4.8×103N/mm2，泊松比υ=0。iGFEM計(jì)算得到的懸臂梁變形過程如圖6所示。圖7比較了懸臂梁自由端的載荷-撓度曲線，再次展現(xiàn)了iGFEM方法的高精度。

6.3 圓桿頸縮

采用圓桿頸縮問題考察本文方法對(duì)于亞彈-塑性材料大變形計(jì)算的有效性。如圖8所示，圓桿長為53.334 mm，半徑為6.413 mm，兩端各施加 7 mm 的固定位移。由于對(duì)稱性，只取圓桿的1/4

圖5 自由端受集中力的懸臂梁

圖6 懸臂梁變形過程

圖7 懸臂梁載荷-撓度響應(yīng)對(duì)比

進(jìn)行數(shù)值模擬。在圓桿中間截面處引入幾何缺陷，該處的半徑為兩端半徑的98.2%。具體的材料參數(shù)和實(shí)驗(yàn)數(shù)據(jù)可以參考文獻(xiàn)[22]。

采用圖9所示的兩種計(jì)算網(wǎng)格，F(xiàn)EM和iGFEM 計(jì)算得到的頸縮曲線與實(shí)驗(yàn)數(shù)據(jù)[22]在 圖10 進(jìn)行了比較。兩種方法計(jì)算得到的圓桿頸縮變形分別如圖11和圖12所示。可以看出，F(xiàn)EM粗細(xì)兩種網(wǎng)格的計(jì)算結(jié)果有明顯差異，而iGFEM粗細(xì)網(wǎng)格的計(jì)算結(jié)果基本保持一致，這在一定程度上驗(yàn)證了iGFEM方法在粗網(wǎng)格下具有良好的高精度特性。

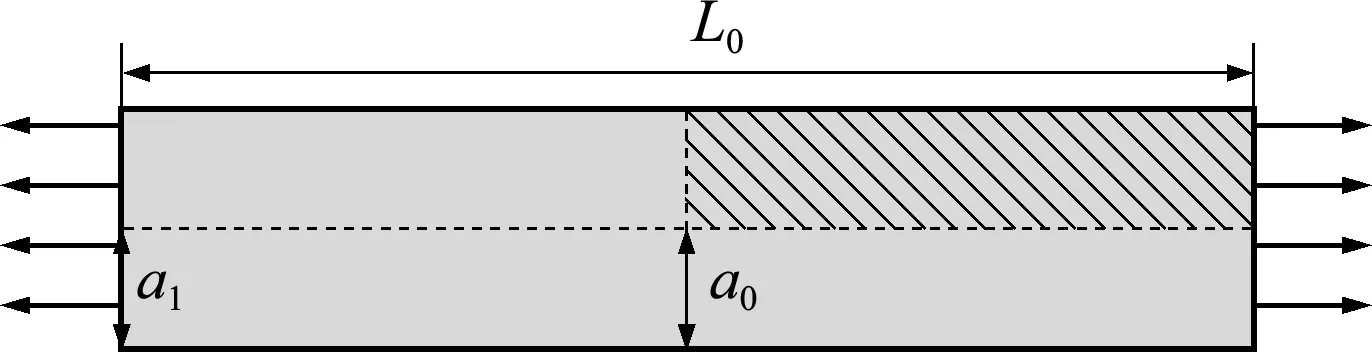
圖8 圓桿頸縮算例

圖9 圓桿頸縮算例的計(jì)算網(wǎng)格

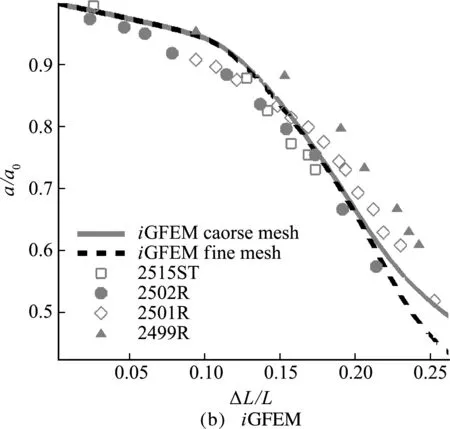
圖10 圓桿頸縮算例的頸縮-位移曲線

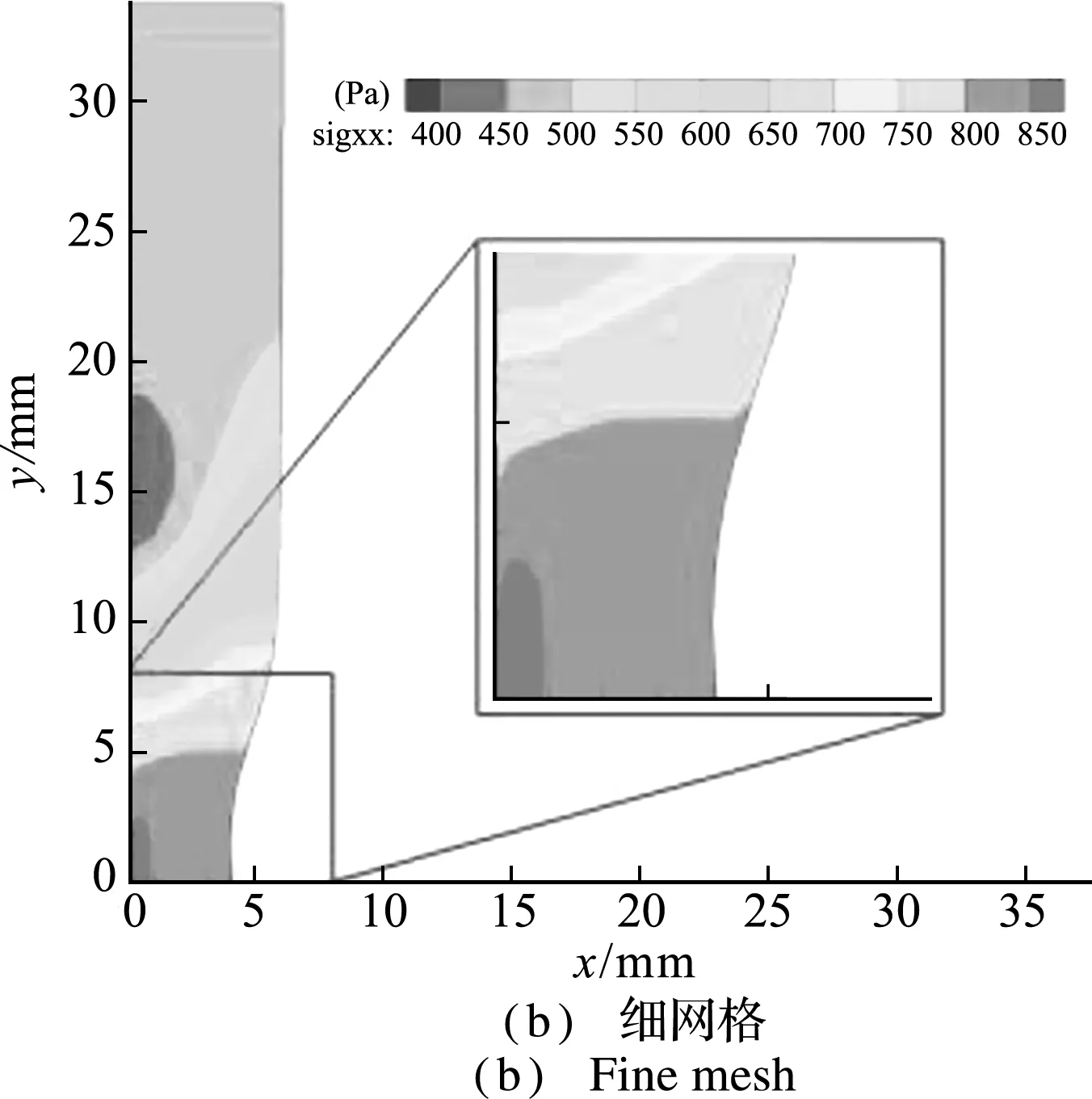
圖11 FEM方法得到的圓桿頸縮變形

圖12 i GFEM方法得到的圓桿頸縮變形

7 結(jié)論與展望

本文建立了幾何和物理非線性分析的無額外自由度廣義有限元方法。數(shù)值結(jié)果表明，本文方法不僅能有效分析彈塑性大變形問題，而且展現(xiàn)出優(yōu)于傳統(tǒng)線性有限元方法的計(jì)算精度。后續(xù)工作將把該方法推廣至三維，面向復(fù)雜工程問題，有力推動(dòng)彈塑性大變形高精度計(jì)算方法的發(fā)展。