基于state -space -split法的滯回非線性系統隨機動力響應分析

徐嚴鋼, 朱海濤*,2, 柳國環, 劉治國,2,3

(1.天津大學 建筑工程學院,天津 300072； 2.天津大學 濱海土木工程結構與安全教育部重點實驗室,天津 300072；3.中國市政工程華北設計研究總院有限公司,天津 300074)

1 引 言

自然界中的地震、風和海浪均具有隨機動力特性[1]。當激勵過大時，工程結構可能會發生局部構件失效，甚至整體破壞，造成巨大的生命和財產損失。因此，研究工程結構在這些隨機激勵下的動力響應特性，提出工程結構隨機動力失效的防護措施，對預防因過大隨機激勵導致工程結構破壞而引發的危害具有重要科學意義和工程價值。隨機激勵下的工程結構響應具有隨機動力特性，早期研究工作將隨機動力荷載等效為靜力荷載，近似計算工程結構的動力響應[2,3]。該等效方法計算的結果與實際工況可能會存在較大偏差，從而導致不安全的設計方案。為了獲得更準確的計算結果，采用隨機振動理論與分析方法是研究工程結構的隨機動力響應的一條有效途徑。采用隨機過程描述隨機激勵輸入，進行工程結構隨機響應分析與動力可靠度驗算。

另一方面，工程結構在地震、風和海浪等隨機激勵作用下產生動力響應，可以采用隨機振動理論將工程結構簡化為隨機動力系統進行分析。當隨機激勵較大時，工程結構動力響應具有幾何非線性特性[4]。同時，在能量耗散過程中，也會呈現材料非線性特性。滯回模型是一種描述材料非線性行為的重要模型。在滯回模型的研究中,Bouc-Wen滯回模型得到廣泛的研究與應用。該模型由Bouc[5]首次提出，隨后Wen[6]進一步完善。Baber等[7，8]研究了其退化現象和Bouc-Wen模型的捏縮效應。

在隨機振動分析方法中，最早由Botton[9]提出的等效線性化法應用最為廣泛，其主要思想是把隨機系統的非線性項進行線性化處理，通過迭代的方法求解出線性化系數，再按照分析線性系統的方法來分析近似后系統的動力響應。許多學者針對等效線性化法進行了改進研究。Caughey[10]通過采用最小方差的原則來確定等效線性化法的參數，同時，對等效線性化法進行了擴展，使其可以運用于多自由度系統的非線性隨機振動研究領域。Er[11]在等效線性化法的基礎上，提出了SSS(state -space -split)法對系統的FPK 方程進行降維來簡化計算。多位學者通過該方法求解了多種隨機振動問題。Zhu[12]采用SSS法求解了在高斯白噪聲激勵下的杜芬形式能量收集器的FPK方程。Er等[13]使用該方法求解了矩形板在高斯白噪聲激勵下的概率密度函數，并對板不同位置處的撓度概率進行了數值研究。

SSS法的優勢在于對高維多自由度復雜激勵下非線性隨機振動問題的簡化計算。該方法可以將高維狀態空間中求解FPK方程的問題轉化成低維狀態空間中求解某些簡化FPK方程的問題,且不受系統狀態自由度數量和非線性強弱的限制，因此可用于分析大規模非線性系統的概率密度函數解。如Er[11]通過該方法求解了外部激勵下的10自由度非線性系統和參數激勵下 8自由度非線性系統等。相比Pushover分析，SSS法基于隨機振動學，分析復雜結構時，采用電腦模擬出的隨機激勵，更接近真實情況。Pushover分析法本質是等效靜力分析方法，側向分布力模式的選取十分重要，當研究較為復雜的結構時，水平分布的側向力并不能完全體現地震的隨機動力特性,結果可能會出現偏差。相比非線性時程分析，SSS法前期簡化過程簡單，損失精度較小，但最終計算結果更依賴于后續方法對簡化方程的計算精度。非線性時程法較為成熟，能真實反映結構在地震作用下的破壞機制和構件的塑性破壞過程,但計算過程過于復雜，實際工程中較難推廣。

綜上所述，針對滯回模型的非線性振動響應以及求解高維非線性問題較有優勢的SSS法已開展了一些研究工作。但是，在研究非線性系統的過程中，通常不同時考慮幾何非線性和材料非線性對響應的影響。故本文探索性地將Bouc-Wen滯回模型引入杜芬非線性系統，同時考慮非線性系統中的幾何非線性和材料非線性，并通過SSS法建立了該非線性系統在高斯白噪聲下的聯合概率密度函數近似求解方法。

2 引入Bouc-Wen模型的杜芬系統

工程結構的非線性主要包括由于結構幾何大變形產生的幾何非線性和由于材料的阻尼產生的材料非線性(如滯回特性)。在土木工程領域中，很多構件都具有滯回特性。如RC框架中形成的塑性鉸和材料的阻尼等。滯回特性通常可以通過應力-應變曲線來直觀表達，帶有滯回特性的構件的應力-應變曲線會在加載和卸載的過程中成為一個閉合的滯回環。

本文基于之前研究，以RC框架結構為例，將Bouc-Wen模型引入杜芬非線性系統。其初始狀態基于以下幾點假設。

(1) 在RC 框架結構的平面振動研究中，將其簡化為質點系模型。

(2) 不考慮柱的軸向伸縮，認為樓板的剛度無限大且只做平動運功，各層的質量都集中在樓板上，在地震的激勵下樓板和各層框架位移相同。

(3) 柱截面滿足平截面假定，橫截面在變形前后垂直于中性軸不改變。

(4) 以剛度屈服比未變化的初始瞬時進行分析，首先不考慮材料非線性引起滯回力的參與，求解出剪力后，再將非線性滯回力按剛度屈服比分配進恢復力中，與線性恢復力和幾何非線性恢復力共同組成非阻尼恢復力。如圖1(a)所示，建立單層單跨的RC框架模型[14],其力學模型如圖1(b)所示。

圖1 單層框架受力模型及力學模型

假設此模型柱長度為H，抗彎剛度為EI，樓板和梁的質量合為m，滯回環形狀控制參數有A，n，β，γ，α∈(0，1)為屈服前后的剛度比，W(t)為地震力，剪力R可表示為[14]

(1)

設此時考慮材料非線性和幾何非線性，系統的振動方程如下。

(2)

式中c=2mζ，ζ為阻尼系數。

當W(t)為地震力時，采用高斯白噪聲ξ(t)來模擬地震的激勵過程。式(12)兩側同除以m，同時考慮經典Bouc-Wen模型(n=1)，則

(3)

3 等效線性化法

采用等效系統殘差均方差最小原則，式(3)的非線性項可以近似為線性項來表示。其等效線性系統如下[15]。

(4)

式中de=3αεE[x2]，ce=βF1+γF2-A，ke=βF3+γF4。參數F1,F2,F3和F4可表示為[7,16]

(5,6)

(7)

(8，9)

(10)

4 State -Space -Split法

將

和z=x3代入式(3)，則原式的一階微分方程組如下：

(11)

此非線性動力系統對應的平穩響應的 FPK 為

(12)

式中p代表p(x1,x2,x3,t)。根據SSS法，對式(12)在x3的域內積分有

(13)

式中p為p(x1,x2)。其中，q(x3|x1,x2)可以通過等效線性化法來得到其近似解。

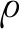
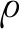
(14)

方差為

(15)

通過SSS法降維后的FPK方程如式(16)所示。其精確解可直接求得。

(16)

(17)

式中K為第二類修正Bessel函數。

D=2ξω+(1-α)ω23(σ3/σ2)

(18)

(19)

(20)

隨后x1,x2和x3的近似聯合概率密度函數可以通過降維后的二維FPK方程精確解和近似條件概率密度函數近似表達：

p(x1,x2)

(21)

5 數值分析

分析非線性模型在均值為0的高斯白噪聲激勵下響應的概率密度函數。選取三個例子以及一個實體工程進行討論，驗證所提方法的適用性。非線性模型的方程見式(3)。參數取值如下,ω=1,ξ=0.05,α=0.5,β=0.5,γ=-0.5,n=1和A=1。

表1 系統參數

采用蒙特卡洛模擬結果對比驗證SSS法的準確性，并與等效線性化法所求得的結果進行比較，證明其優越性。計算結果如圖2～圖4所示。其中蒙特卡洛法產生的樣本數為1000萬。由SSS法、等效線性化法和蒙特卡洛法求解的結果分別簡寫為SSS，EQL和MCS。概率密度函數簡寫為PDF。

算例1的結果如圖2所示。圖2(a,e)表明激勵強度和非線性系數均較低時，在位移PDF的峰值區域和尾部區域，相比EQL，SSS和MCS的擬合程度更好。表明此條件下的位移PDF是非高斯分布的。圖2(b,f)是速度PDF圖。對于速度PDF，SSS和EQL結果相同。對于峰值區域，兩者均存在偏差；對于尾部區域，兩者精確度都較好。圖2(c,g)為滯回力PDF分布。對于峰值區域，SSS和EQL均存在少量誤差，不能精確地描述峰值區域；對于尾部區域，SSS和MCS存在少量誤差，誤差小于EQL。這證明了在激勵強度和非線性系數較低時，相對EQL法，SSS法可以更好地描述位移和滯回力的PDF，尤其是尾部區域。圖2(d，h)為算例1的位移-速度聯合分布。從位移方向來看，在[-0.5,0.5]區間內，EQL結果略大于SSS的結果。而在[-0.5,0.5]區間外，SSS的結果分布更寬于EQL的結果，分布趨勢近似于位移PDF的趨勢。

圖2 算例1概率密度函數的分布

算例2的結果如圖3所示。如圖3(a,e)所示，保持幾何非線性系數不變，增大激勵，對于位移PDF，EQL和MCS的誤差增大，而SSS和MCS的擬合依然良好。隨著激勵的增大，位移PDF逐漸遠離高斯分布，且EQL法精度降低。圖3(b,f)表明，EQL和SSS依然相同且精度較高,精度不受激勵影響。圖3(c,g)為滯回力的PDF。對于峰值區域，兩種結果都和MCS存在誤差，EQL的誤差較小；但對于尾部，SSS誤差更小。激勵增大后，SSS法能較好地描述滯回力PDF的尾部區域。圖3(d,h)為算例2的位移-速度聯合分布。從位移方向來看，在[-1,1]區間內,EQL大于SSS；在[-1,1]區間外，SSS分布比EQL廣泛。激勵增大導致聯合分布的范圍變得更廣,峰值降低。

圖3 算例2概率密度函數的分布

算例3結果如圖4所示，保持激勵大小不變，增大非線性系數。如圖4(a,e)所示，對于位移PDF，SSS和MCS擬合較好，而EQL誤差偏大。在非線性系數和激勵均較大時，EQL法精度明顯降低。圖4(b,f)是速度PDF，三者幾乎重合，速度PDF呈高斯分布。圖4(c,g)為滯回力PDF，對于峰值區域，EQL誤差偏小；而對于尾部，EQL存在著較大的誤差，SSS能保持較高的擬合精度。圖4(d,h)為算例3的位移-速度聯合分布。其趨勢與 圖3(d,h)相似。在峰值處，EQL和SSS結果相差更大。這與算例2和算例3的位移PDF分布的差異情況相似。

采用SSS法和蒙特卡洛法，通過首超破壞機制中的單側安全界限機制和破壞準則，計算一榀單層混凝土框架結構在平穩高斯白噪聲激勵下的可靠度,驗證其實用性。取激勵強度S0=0.002 m2/s3，結構自振頻率為w0=12 rad/s，阻尼比ζ=0.05，高度H=13.2 m，ε=6.198。Bouc-Wen模型的參數采用劉俊等[17]通過參數識別所獲得的模型參數，α=0.2,β=0.202,γ=0.3147,n=1,A=1.1037，單側安全界限b=2.4 cm。結構動力可靠度公式如下。

(22)

從圖5可以看出，當t=9 s時，響應達到平穩。從圖6可以看出，SSS法計算結果與MCS結果幾乎吻合，證明了該方法準確度接近數值模擬結果，在工程上可行。

圖4 算例3概率密度函數的分布

圖5 二階矩變化曲線

圖6 動力可靠度變化

6 結 論

采用SSS法分析了一類同時擁有幾何非線性和材料非線性的非線性隨機動力系統的響應，獲得了系統在高斯白噪聲激勵下平穩響應的概率密度函數，并通過實例驗證了其有效性。研究表明，

(1) 在求解位移PDF 時，當激勵較小時，SSS法和EQL法對峰值區域求解精度較高。對于尾部區域，激勵增大后，EQL法求解會產生較大誤差而SSS法能保持較高的求解精度。

(2) 求解速度PDF時，SSS法和EQL法計算的結果相同，且速度概率密度函數分布始終保持近似高斯分布。

(3) 求解滯回力PDF時，在峰值區域，隨激勵增大，兩種方法都不能很好地對PDF進行描述。對于PDF的尾部，SSS法的求解精確度更好。工程結構的破壞往往和PDF尾部關系比較緊密，因此分析PDF尾部分布有重要意義。SSS法在分析這類非線性模型隨機振動問題時，可以提供更精準的概率密度函數解。

(4) 當幾何非線性系數增大時，EQL求解的誤差會增大，而SSS法可以保持較高的精度。

(5) 本文主要研究 SSS法求解復雜非線性滯回模型在均值為零的高斯白噪聲激勵下平穩響應的可行性和適用性。但對于地震作用下的橋梁等土木建筑結構，更多采用過濾白噪聲或考慮非平穩過程。當考慮過濾白噪聲激勵時，需在原振動方程組中增加一濾波器方程，得到相應的FPK方程，再采用SSS法進行降維運算。關于SSS法的詳細降維運算過程可參見文獻[11]。對于非平穩過程，SSS法需要進一步研究，使該方法可以拓展解決非平穩問題。