解兩點邊值問題的一種新方法

張杰華,周實然

(1.凱里學院理學院,貴州 凱里 556011)

(2.凱里學院教育科學學院,貴州 凱里 556011)

1 引言

隨著微分方程理論的不斷發展,兩點邊值問題的研究也日益活躍,它在工程力學、天文學、經濟學、控制論及生命科學等領域的許多實際問題中都有著廣泛的應用.有限體積法,又被稱之為廣義差分法、控制體積法,它兼顧了有限差分法和有限元法各自的優點,是求解偏微分方程的一種有效數值方法[1].

眾所周知,有限元法及其超收斂理論研究已經比較完善[2,3],而有限體積法的研究還不盡人意.關于求解兩點邊值問題的有限體積法研究,多年來碩果累累.上世紀八、九年代,學者們已經開始致力于有限體積法的基礎理論研究[4–7].到了本世紀初,關于高階有限體積法及其超收斂理論分析的研究,開始逐漸成為關注的熱點,進入學者們的視野[8–15].特別地,文獻[16]證明了線性有限體積法的解與相應的有限元法的解具有H1模超逼近性質.專著[17]給出了兩點邊值問題二階與三階有限體積法的H1模超逼近及其應力佳點的超收斂結論.文獻[18]建立了基于應力佳點的三階有限體積法并得到了關于其導數誤差估計的超收斂結果.文獻[19–21]給出了兩點邊值問題的任意階有限體積法在節點處與高斯點處的超收斂分析.雖然,大部分的這些研究工作分析了對應的有限體積法的最優H1模和L2模誤差估計,給出了應力佳點處的導數誤差估計以及整體的H1模超收斂結果,但都很少提及有限體積法的L2模超逼近和超收斂后處理估計.

此外,近年來基于三角形網格剖分的有限體積法研究也取得了突破性的進展.文獻[22,23]借助于離散范數等價,在三角形網格上分析了一類橢圓問題的高階有限體積法的強制性要求.文獻[24]通過選取特殊的三角形對偶剖分,利用從試驗函數空間到檢驗函數空間的特殊映射,構建了與三角形形狀無關的無條件穩定的二階有限體積法.正是這些已有的研究成果啟發了本文的工作.

本文基于Lagrange二次有限體積法,構造求解兩點邊值問題的一種新Lagrange二次數值方法,得到了新方法的H1模和L2模的超逼近估計.具體地,基于有限體積法[24]構造特殊對偶剖分及其特殊映射的思想,引入從Lagrange二次有限體積法的試驗函數空間到檢驗函數空間的一個新映射,從而得到求解兩點邊值問題的一種Lagrange二次新數值方法.此數值方法在特殊對偶剖分時即為Lagrange二次有限體積法.借助于文獻[22,23]中離散等價范數的技巧,利用等價二次型的性質,本文構造了與H1模,H2離散半模等價的離散范數,證明了對任意的Lagrange二次對偶剖分此文的數值方法均具有最優H1模誤差估計.特別地,當對偶剖分單元節點取為應力佳點(Gauss點)時,本文分析了新數值方法的第一型和第二型插值弱估計,從而得到了H1模和L2模的超逼近估計(第二型插值弱估計是得到L2模超逼近的關鍵).對此特殊對偶剖分的數值解作局部二級插值處理,則可得到新數值方法的整體H1模和L2模超收斂估計,其收斂階與其對應的二次Lagrange有限元法結論一致.利用本文的技巧,同樣可分析Lagrange二次有限體積法的超收斂結論.另外,本文的思想與方法可以擴展至高維高階的數值方法情形.

下一節,本文將給出求解兩點邊值問題的Lagrange二次新數值方法.第三節將給出離散范數等價估計.第四節考慮對任意二次對偶剖分新數值方法的最優H1模誤差估計.第五節,采用特殊對偶剖分,分析新數值方法的第一型及第二型插值弱估計,并證明數值解的H1模和L2模超逼近估計,以及利用二級插值處理后的超收斂估計.最后,給出數值算例,說明本文理論結果的正確性.

2 新Lagrange二次數值方法

方程(2.6)即為本文所分析的求解兩點邊值問題的Lagrange二次新數值方法.

3 等價范數

4 H1誤差分析

book=180,ebook=89

5 超收斂估計

6 算例

本節給出數值算例,驗證數值方法(2.6)的有效性及其超逼近,超收斂估計.本文中的所有數值計算均是在個人PC機上利用Matlab(R2010b)軟件計算得到.采用GMRES迭代方法求解線性方程組(2.6),取其截斷誤差為10?10.表格中的,h為單元長度.

考慮如下兩個兩點邊值問題.

例 6.1設方程(2.1)中的p(x)=1,a=0,b=1,其真解為u=exsin(πx)+πex?π,x∈(0,1).顯然有u(0)=u0(1)=0.

例 6.2設方程 (2.1)中的p(x)=e?πx,a=0,b=1,其真解為u=eπxsin(πx)+πeπx,x∈(0,1).顯然也有u(0)=u0(1)=0.

表1和表2列出了數值方法(2.6)關于例6.1的計算結果.其中,取參數.從表1的數值結果不難發現,數值方法(2.6)具有最優階H1模誤差估計和H1模,L2模超逼近估計.而表2的數值結果顯示,數值方法(2.6)的解經過二級插值處理之后具有H1模,L2模超收斂結果.這些數值結果與本文的理論結果相一致,且與相對應的有限元法具有相同的收斂階.

表1 數值方法(2.6),例6.1,

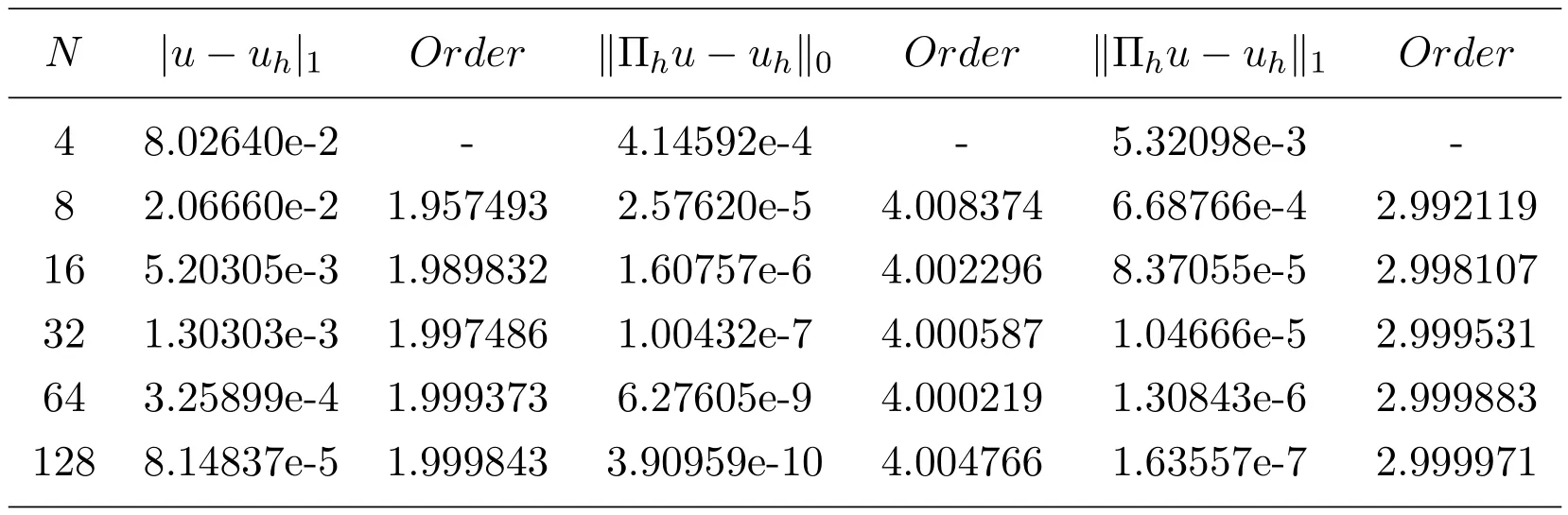
表1 數值方法(2.6),例6.1,

N |u?uh|1 Order kΠhu?uhk0 Order kΠhu?uhk1 Order 4 8.02640e-2 - 4.14592e-4 - 5.32098e-3 -8 2.06660e-2 1.957493 2.57620e-5 4.008374 6.68766e-4 2.992119 16 5.20305e-3 1.989832 1.60757e-6 4.002296 8.37055e-5 2.998107 32 1.30303e-3 1.997486 1.00432e-7 4.000587 1.04666e-5 2.999531 64 3.25899e-4 1.999373 6.27605e-9 4.000219 1.30843e-6 2.999883 128 8.14837e-5 1.999843 3.90959e-10 4.004766 1.63557e-7 2.999971

表2 數值方法(2.6),例6.1,

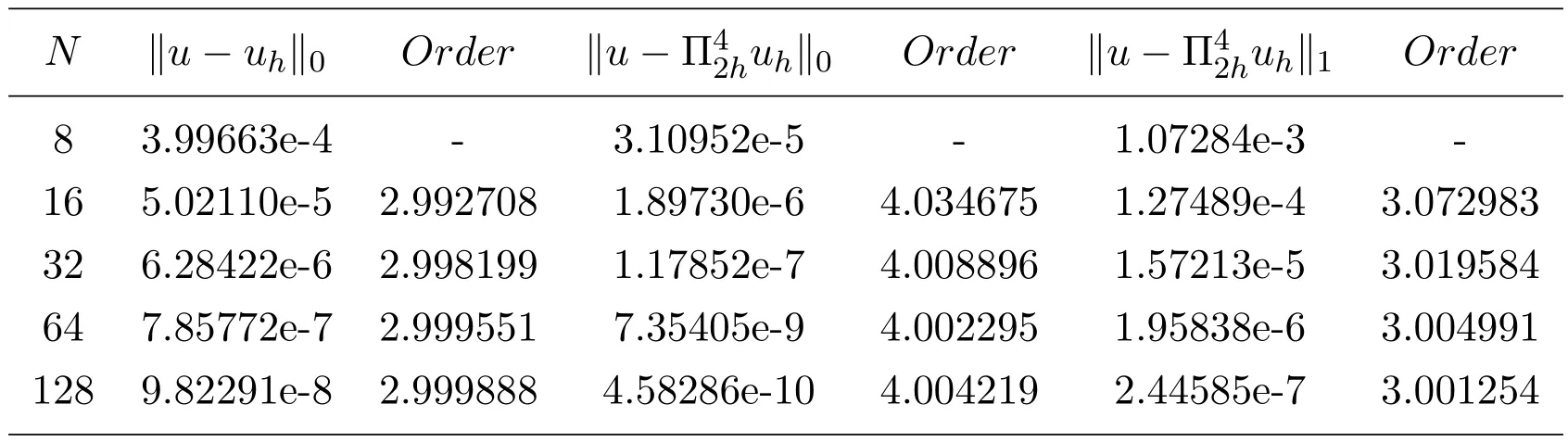
表2 數值方法(2.6),例6.1,

N ku?uhk0 Order ku?Π42huhk0 Order ku?Π42huhk1 Order 8 3.99663e-4 - 3.10952e-5 - 1.07284e-3 -16 5.02110e-5 2.992708 1.89730e-6 4.034675 1.27489e-4 3.072983 32 6.28422e-6 2.998199 1.17852e-7 4.008896 1.57213e-5 3.019584 64 7.85772e-7 2.999551 7.35405e-9 4.002295 1.95838e-6 3.004991 128 9.82291e-8 2.999888 4.58286e-10 4.004219 2.44585e-7 3.001254

表3列出了數值方法(2.6)關于例6.2的最優階H1模誤差估計和H1模,L2模的超逼近估計.表4列出了數值方法(2.6)關于例6.2的H1模,L2模的整體超收斂結果.其中參數仍取.其數據結果再次表明,本文采用的數值方法(2.6)對變系數p(x)的兩點邊值問題是有效的,且具有最優階H1模誤差估計,H1模和L2模的超逼近及超收斂結果.

表3 數值方法(2.6),例6.2,

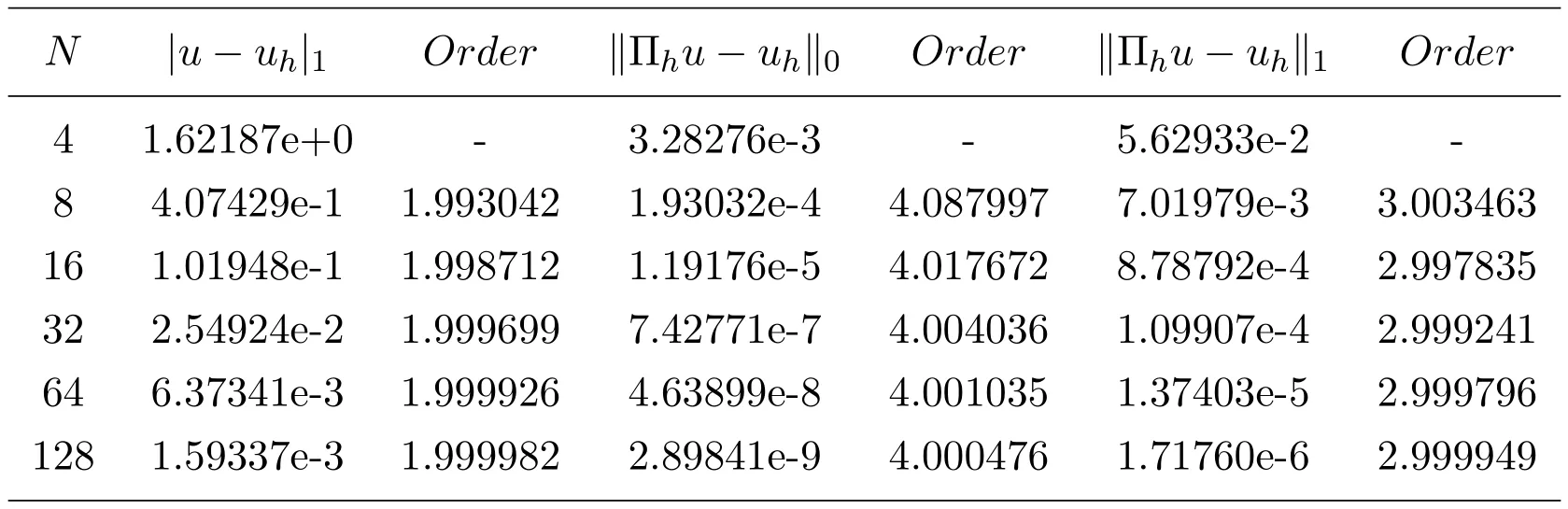
表3 數值方法(2.6),例6.2,

N |u?uh|1 Order kΠhu?uhk0 Order kΠhu?uhk1 Order 4 1.62187e+0 - 3.28276e-3 - 5.62933e-2 -8 4.07429e-1 1.993042 1.93032e-4 4.087997 7.01979e-3 3.003463 16 1.01948e-1 1.998712 1.19176e-5 4.017672 8.78792e-4 2.997835 32 2.54924e-2 1.999699 7.42771e-7 4.004036 1.09907e-4 2.999241 64 6.37341e-3 1.999926 4.63899e-8 4.001035 1.37403e-5 2.999796 128 1.59337e-3 1.999982 2.89841e-9 4.000476 1.71760e-6 2.999949

表4 數值方法(2.6),例6.2,

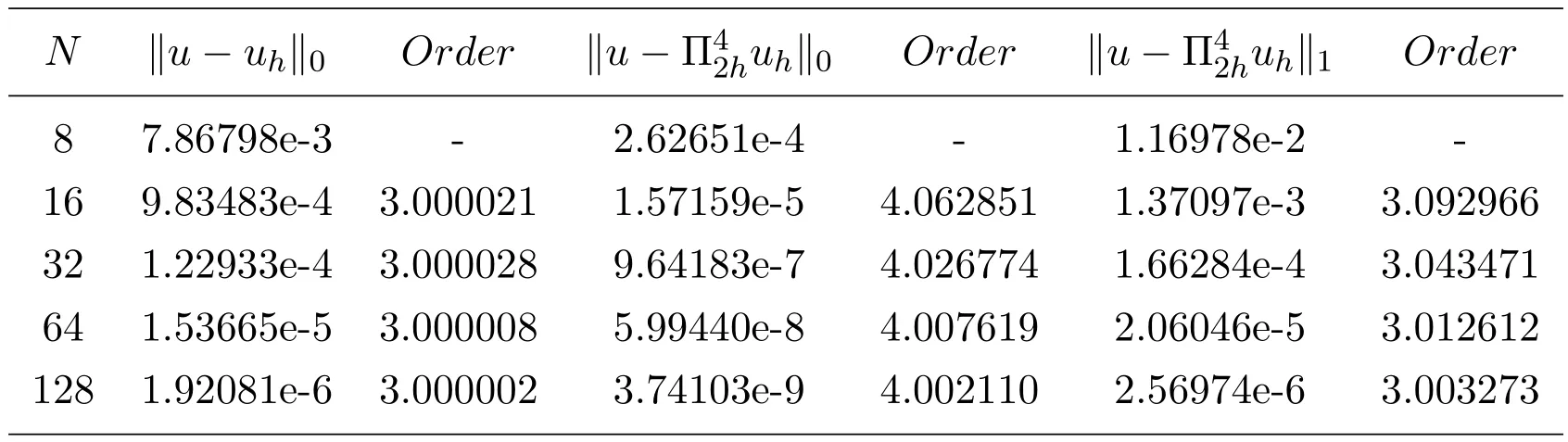
表4 數值方法(2.6),例6.2,

N ku?uhk0 Order ku?Π42huhk0 Order ku?Π42huhk1 Order 8 7.86798e-3 - 2.62651e-4 - 1.16978e-2 -16 9.83483e-4 3.000021 1.57159e-5 4.062851 1.37097e-3 3.092966 32 1.22933e-4 3.000028 9.64183e-7 4.026774 1.66284e-4 3.043471 64 1.53665e-5 3.000008 5.99440e-8 4.007619 2.06046e-5 3.012612 128 1.92081e-6 3.000002 3.74103e-9 4.002110 2.56974e-6 3.003273

表5 數值方法(2.6),例6.2,

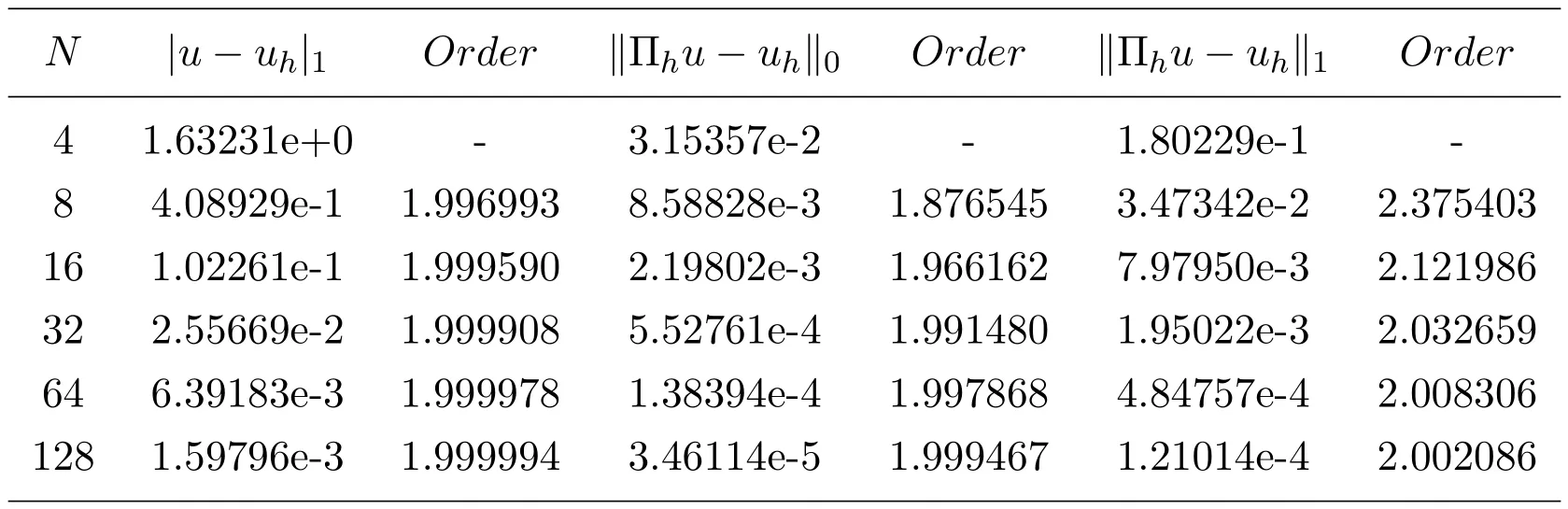
表5 數值方法(2.6),例6.2,

N |u?uh|1 Order kΠhu?uhk0 Order kΠhu?uhk1 Order 4 1.63231e+0 - 3.15357e-2 - 1.80229e-1 -8 4.08929e-1 1.996993 8.58828e-3 1.876545 3.47342e-2 2.375403 16 1.02261e-1 1.999590 2.19802e-3 1.966162 7.97950e-3 2.121986 32 2.55669e-2 1.999908 5.52761e-4 1.991480 1.95022e-3 2.032659 64 6.39183e-3 1.999978 1.38394e-4 1.997868 4.84757e-4 2.008306 128 1.59796e-3 1.999994 3.46114e-5 1.999467 1.21014e-4 2.002086

7 結論

本文構造了求解兩點邊值問題的一種新Lagrange二次數值方法,利用等價離散范數證明了該方法的第一型與第二型弱估計,從而得到該數值方法的整體H1模和L2模超逼近結果,其收斂階與對應的有限元法結果相一致.本文的思想與方法可以擴展至高維高階的有限體積法情形.