考慮相對財富的前景理論價值函數對比研究

陶剛

（貴州師范大學 經濟與管理學院，貴州 貴陽 550001）

一、引言

對于人類的風險偏好的探究是更好地理解經濟現象的本質出發點，本文通過行為實驗數據，重點研究前景理論（Prospect Theory，簡稱“PT”）中的價值函數，并將模型擴展，嘗試將個人財富因素納入模型，進行對比研究。考慮了個人財富因素的模型簡稱“PT-RW”，其中RW代表相對財富（Relative Wealth），PT 模型中考慮的是絕對財富量變化引起的心理效應的改變，但是相對于個人財富總量的財富變化更能有效地反映相應的心理效應，即“RW（Δw）=絕對財富量的變化÷個人總財富”。具體下文從三個維度進行對比研究：一是納入個人財富因素的價值函數模型（PT-RW）在總體解釋力上是否會強于原PT 模型；二是價值函數在負定義域的凹凸性有爭論，本文對此維度進行比較研究；三是正負回報的加權函數π 是否一致，即π+=π-。本文對PT 和PT-WR 的函數模型進行分析，并設計實驗收集數據，對模型進行檢驗，計量方法選取的是普通最小二乘法（Ordinary Least Squares，簡稱“OLS”）與非線性最小二乘法（Non-linear Least Square，簡稱“NLS”）。

二、模型

PT 價值函數理論形式為：

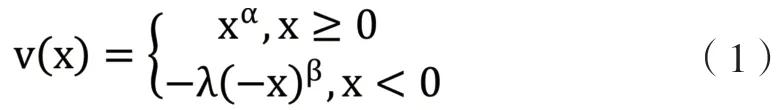
實驗問題中有一組完全正回報風險資產的問題，可以由這組問題估計出PT 價值函數的α參數。具體的有：

其中x1i與x2i為實驗問題直接列出的風險資產中的兩個或有狀態回報，并假定心理參照點就是自己擁有的財富量，權重函數π 由于概率固定在一點上，所以作為常參數來估計，Gi為正回報風險資產問題中所誘導出的確定性等價。

納入了個人財富因素的模型PT-RW 函數形式為：

PT-RW 價值函數形式顯得復雜，但在非混合回報的情況下總能分別退化為兩個簡單的冪函數形式，因此在估計模型選擇上同樣采取了和PT 價值函數相同NLS 計量模型，只需要在變量上進行一些處理，用到實驗問題中直接列出的風險資產的兩個回報以及被試的財富量數據。

PT 價值函數中用參數λ 來表示損失厭惡系數，為此需要專門設計一組實驗問題來估計參數λ，這個估計問題還要把預先對PT 的非混合回報情形估計出的參數α 跟β 帶入，才能使用進一步估計參數λ。注意式（4）中沒有權重函數，這是因為將概率值固定在0.5。關于0.5的概率劃分，稍微回顧理論就可發現這樣一種安排將權重函數的部分恰好消去。

其中，x1i是在實驗中設定好的數據，x2i是實驗誘導出的數據。

由于非線性最小二乘估計在計量軟件中不報告擬合優度R2，需要在最后一組混合回報的問題中通過普通最小二乘法來比較兩個價值函數對數據的解釋力，只要把第一組、第二組、第三組實驗問題中對PT 估計的參數α、β、λ 以及對PT-RW 估計的參數α、β 帶入，生成新的變量，就可利用OLS 報告的擬合優度來比較兩個模型的解釋力。

三、估計方法

以正回報風險資產檢驗原假設H0：π1+π2=1為例。首先估計完全模型：

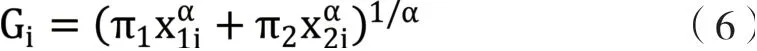
記為模型Full。然后將約束條件帶入π1+π2=1，估計約束模型：

記為模型Reduced。分別從兩次回歸中記錄相關統計量，然后計算：

其中RSS 代表殘差平方和，df 代表自由度，n 為觀測點數。再讓統計量F 與其分布的拒絕域比較，即可檢測原假設π1+π2=1的真偽。若檢測約束條件為真，將在最后模型比較時的參數代入中使用約束模型估計出的參數。

對于原假設H0：π+=π-的檢驗，在有一個狀態回報為零的情況下其等價于檢驗H0：π+=π-，現在需要把正、負回報的問題合并到一個數據集中，并生成標識變量，若為負回報標識變量TX=1，若為正回報TX=0，生成變量yi，當為正回報時其等于Gi，為負回報時等于Li，則可估計模型：

在此模型中令π+Δ 為π-，π 為π+，所以檢驗原假設π+=π-，進一步簡化為檢驗參數Δ 是否為0。對于PT-RW 價值函數的估計方法可以沿用同樣的思路。

四、實驗設計

獲取被試的確定性等價數據（Certainty Equivalent，簡稱“CE”）是本文研究的關鍵。實驗經濟學家強調確定性等價由實驗誘導出，而不是憑被試自己口述報告的重要性。確定性等價可以理解為對一支風險資產的估值，假設一支風險資產L，你對其估值￥1000，也就是說1000是你對這支風險資產的確定性等價，在實驗中如果出價1010，你就不愿意買L，而出價990，你就愿意買L，那么就說你的確定性等價在（990，1010）這個價格區間。在文獻中通常用區間的中值作為確定性等價的估計值，若實驗越精細，價格區間越小，那么就越逼近被試者的確定性等價真實值。本文選取貴州某大學學生作為實驗被試。實驗一共有兩輪，一輪實驗中又分為上下兩節，每節時長45分鐘，中間有10分鐘休息時間，兩輪實驗間隔一周。初選被試共92名同學，剔除異常值，有80個有效反饋，其中55名男生、25名女生。

在兩輪實驗中需要獲得兩類信息，一是四組風險資產的確定性等價，二是個人財富數據。由于在資產狀況變化不大的時候總可以認為人的效用是線性的，所以刻意讓或有回報的數值較大，以便于更準地測定效用函數的彎曲程度。在第一輪實驗中進行的是兩組非混合回報風險資產問題的測試，并且在開始時，有一組預熱問題讓被試熟悉他們將回答的選擇問題，被試也被告知選擇并無對錯之分，回答問題過程中可以暫停并休息。大學生沒有真正屬于自己的財富積累，絕大部分同學還都是靠父母資助。實驗選取的是學生的學期消費作為被試財富的代理變量，因為這個數據既容易被被試自己估計，又能相對全面地反映學生消費能力，如果默認消費能力和財富有相對穩定的關系，就有理由讓這個數據作為被試財富量的代理變量。

在第一輪實驗中，給被試展示的兩組非混合回報風險資產問題如表1所示。

表1 非混合回報風險資產確定性等價誘導問題

確定性等價的誘導過程如下：以風險資產（400，0.5，2000）為例，首先展示其均值1200，如果被試的選擇偏好為（400，0.5，2000）＜1200的話，即被試在這兩個資產間選擇1200，那么將確定性資產1200的數值下降25%到900，若仍為（400，0.5，2000）＜900，繼續下降到675，若（400，0.5，2000）＞900，那么從900上升25%到1125，重復5次后找到區間a ＜（400，0.5，2000）＜b，最后以（a+b）/2代表其確定性等價，其他組的誘導過程沿用相同辦法。在第一輪中對被試進行學期消費分類問卷，除去學校必要花費，比如學費、住宿費及書費，調查個人的學期基本餐飲消費、社交活動餐飲消費、通信費、是否旅游及旅游消費、更換幾次手機及相應花費、文化活動消費如演唱會及展覽、衣物購買消費。學生填于問卷表上，反饋回來再對其逐項加總。

第二輪中的兩組風險資產問題如表2所示。

表2 混合風險資產正回報誘導問題

其中第三組實驗問題是專門設計來測試PT 價值函數中參數λ 的，（-1200，0.5，x2）表示如果有五成可能賠￥1200，那么這個博彩中贏面的獎勵x2要是多少你才肯接受這個博彩，x2就是第三組問題中要誘導出的數值。第四組問題誘導出確定性等價后，將前三組問題中分別得到的PT 與PT-RW 價值函數的參數帶入，生成新的變量，就可以利用OLS 來比較兩個價值函數對于實驗數據的擬合優度，進而看出哪個模型對數據的解釋能力更強。第四組問題如表3所示。

表3 混合風險資產確定性等價誘導問題

五、實驗結果

被試學生的消費數據統計顯示，最大值為￥11528，最小值￥1251，均值￥4107，標準差￥2049，中位數￥3315。數據偏態為右偏，表明大部分人消費能力低，較小部分人群的消費能力高。學期消費從￥2500到￥4500的樣本有54個，占總樣本的67.5%。表4為第一組實驗問題的NLS 參數報告，第一組中全是正回報風險資產，因此測出的是PT-RW 與PT 價值函數的參數α 及相應的權重函數。每個價值函數又分為無約束模型和約束模型來進行回歸反洗，約束條件為π1+π2=1，括號中報告的是95%置信區間。NLS 參數初值設定為α=1，π1=π2=0.5。無論用PT-RW 還是PT 的價值函數，都無法拒絕原假設π1+π2=1。因此在第四組問題中PT-RW與PT 價值函數模型比較時帶入約束模型的參數，PT-RW 價值函數帶入α=0.5205，PT 價值函數則帶入α=0.9481，可見兩個價值函數估計的α 在正回報風險資產的情況下差別明顯，且表現為PT-RW 價值函數模型在正回報情形下函數彎曲程度更大。

表4 正回報風險資產問題的NLS 參數估計

表5是在負回報風險資產的第二組測得的參數，仍然無法拒絕原假設π1+π2=1。兩價值函數估計得到的β 差別不明顯，但是比較原模型會發現若PT-RW 價值函數的β＜1，則在負定義域表現為凹函數，而PT 價值函數的β＜1，則在負定義域表現為凸函數，但總體來說相對于正定義域的函數，負定義域函數都更接近于直線。具體在第四組問題中比較兩個價值函數的解釋力時，代入的PT-RW 價值函數參數β 為0.9686，代入的PT 價值函數參數β 為0.9826。可見用實驗數據，PT 模型NLS 結果仍然能得到負定義域函數為凸的結論，但是融入個人財富的PT-RW 模型，能讓凸函數轉變為凹函數。若價值函數全局為凹，那么和經典經濟理論就有更優的融合度。將第一組和第二組數據結合起來測試原假設π+=π-，其中π+相當于第一組問題的π2，π-相當于第二組問題的π1。無論用PT-RW 還是PT 的價值函數都無法拒絕原假設π+=π-。在第三組問題中測得λ=1.9146。

在用OLS 方法對PT-RW 和PT 價值函數的比較中，發現PT-RW 的擬合優度為43%，大于PT 函數的擬合優度26%。且PT 的OLS 模型中截距項在5%置信水平下顯著不為零，而參數π1并不顯著。由此可見在本組數據中融入了個人財富數據的PT-RW 價值函數解釋能力確實高于沒有融入個人財富數據的PT 價值函數。如表6所示。

表5 負回報風險資產問題的NLS 參數估計

表6 兩個理論價值函數模型的解釋力比較

六、結語

雖然實驗條件簡單，但本次實驗仍然取得了許多積極的成果，原因主要有兩點：一是相對于經典文獻的實驗，本次實驗所獲得的樣本量更大；二是放棄對權重函數的全局估計而專注于對價值函數的比較。其中最為主要的成果是PT-RW 價值函數相對PT 價值函數對實驗數據的解釋能力更強，雖然PT-RW 價值函數中減少了一個參數，僅有的兩個參數不僅刻畫正定義域以及負定義域函數曲線的彎曲程度，還要刻畫損失厭惡這一重要的心理現象，但是相對PT 價值函數，PT-RW 價值函數在自變量中融入了個人財富這一影響人類風險態度的重要因素，也許這正是其數據解釋力更強的一個關鍵因素。PT-RW 價值函數支持負定義域效用函數為凹的假說，全局為凹的價值函數和許多傳統經典經濟理論相融更加容易，并且價值函數在負定義域中的凹性與人類面對負回報風險資產時表現出的風險偏好的特性也不矛盾。綜上，本文的研究從實驗方法到研究結論，為從行為經濟角度更好地理解人類價值選擇偏好進行了有益的嘗試。