基于擴展卡爾曼濾波的XPNAV-1衛星自主定軌算法研究

丁陶偉，帥平，黃良偉，張新源

中國空間技術研究院 錢學森空間技術實驗室，北京 100094

X射線脈沖星屬于高速旋轉的中子星，具有極穩定的周期性。利用X射線脈沖星導航能夠為航天器提供包括時間、位置、速度和姿態在內的全面的導航參考信息，為解決近地軌道和深空探測航天器的持續高精度自主導航難題提供了一種新思路。近十余年來，利用X射線脈沖星的航天器自主導航一直是國內外航天前沿技術研究的熱點領域[1-2]。2004年，美國國防部國防預先研究計劃局(DARPA)提出“X射線導航與自主定位驗證(XNAV)”計劃[3]，其目標是建立一個脈沖星網絡，利用脈沖星輻射的X射線信號實現航天器長時間自主導航。自2005年以來，中國持續開展X射線脈沖星導航系統理論與方法研究，研制了多種類型的X射線探測器產品、脈沖星導航地面試驗系統和脈沖星導航專用試驗衛星[4]。2016年11月10日，中國成功發射全球首顆脈沖星導航專用試驗衛星——X射線脈沖星導航1號(XPNAV-1)，率先開展脈沖星導航空間飛行試驗[5-6]。2017年6月3日，美國宇航局(NASA)將“空間站X射線計時與導航技術試驗(SEXTANT)”設備發射到國際空間站(ISS)上，開展脈沖星導航在軌演示驗證試驗[7]。該試驗項目是“中子星內部結構探測器(NICER)”任務之一，其X射線計時儀的有效探測面積大于1 800 cm2，探測能譜范圍為0.2～1.2 keV。

在利用X射線脈沖星的航天器自主軌道確定算法研究方面，前人已經進行了大量研究工作，主要包括針對模型不確定性的魯棒濾波算法[8]、為降低非線性影響的非線性預測濾波(NPF)算法[9]、針對脈沖星方向誤差的擴展狀態無跡卡爾曼濾波(ASUKF)算法[10]、基于多模自適應估計的無跡卡爾曼濾波(UKF)算法[11]等，但這些算法都是利用仿真數據來實現的。目前，美國戈達德太空飛行中心(GSFC)利用SEXTANT設備的觀測數據開展軌道確定試驗，但尚未檢索到其具體定軌算法。XPNAV-1衛星在軌運行4年來，獲取了大量觀測數據，按計劃完成了X射線探測器性能測試、典型目標脈沖星觀測及脈沖星導航系統體制驗證等試驗任務[12-14]。利用XPNAV-1衛星對蟹狀星云(Crab)脈沖星的完整觀測數據，采用基于軌道法平面幾何約束方法，驗證了該衛星軌道改進的有效性和脈沖星導航系統體制[15]，但利用單顆脈沖星的觀測數據長時間定軌過程存在發散問題。本文針對XPNAV-1衛星拓展任務及后續發展需求，建立其軌道力學模型和觀測方程，并論述擴展卡爾曼濾波(EKF)算法和分段式定常系統(PWCS)的可觀測性分析方法。

1 XPNAV-1衛星任務

XPNAV-1衛星是一顆整星質量為243 kg的小衛星。其科學試驗目標是：1)在空間環境下實測驗證X射線探測器性能，研究宇宙背景噪聲對探測器作用機理；2)探測Crab脈沖星輻射的X射線光子，提取脈沖輪廓曲線；3)長時間累積探測脈沖星，積累觀測數據，探索驗證脈沖星導航體制。

XPNAV-1衛星采用降交點地方時為6:00時的太陽同步晨昏軌道，其軌道半長軸為6 878.137 km，軌道傾角為97.4°，偏心率為0.010 3。該衛星的有效載荷為兩種不同類型的X射線探測器。其中一種是掠入射式聚焦型探測器，其有效面積為30 cm2，探測能譜范圍為0.5～10 keV，時間分辨率為1.5 μs，視場為15′；另一種是微通道板準直型探測器，其有效探測面積為1 200 cm2，探測能譜范圍為1～10 keV，時間分辨率為100 ns，視場為2°。針對核心試驗任務需求，優選了8顆目標脈沖星進行重點觀測研究，其脈沖星編號、J2000.0國際天球參考系下的赤經和赤緯、脈沖周期及光子流量如表1所示。表1中，序號1～4為獨立旋轉供能脈沖星(IRP)，其中第1顆脈沖星B0531+21為Crab脈沖星，序號5～8為X射線雙星(XB)。

XPNAV-1衛星在軌運行近4年來，對8顆目標脈沖星、超新星遺跡以及銀河系X射線等天體進行了觀測研究。由表1可見，XB的光子流量比IRP高2～3個數量級，觀測XB的主要目的是進行探測器性能測試。考慮到XB系統本身軌道動力學的復雜性，本文主要利用上述4顆IRP開展自主定軌算法研究。

表1 8個候選觀測對象參數列表

2 XPNAV-1衛星自主定軌數學模型

XPNAV-1衛星軌道為太陽同步軌道，在軌道可見性分析過程中要求脈沖星方向與太陽夾角大于45°，與月球夾角大于5°，并且要考慮地球遮擋、規避南大西洋異常區和高緯度極區輻射等約束條件。針對該衛星軌道特點，建立軌道力學模型和自主定軌觀測方程。

2.1 軌道力學模型

XPNAV-1衛星軌道力學方程可表示為:

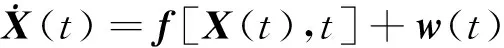
(1)

式中:X(t)為狀態變量；f[X(t),t]為軌道動力學方程；w(t)為系統噪聲項。

在該衛星自主定軌研究中，采用只考慮地球中心引力加速度和J2項非球形攝動加速度的衛星軌道力學模型，代入式(1)得到衛星軌道力學方程:

(2)

式中:r=[rx,ry,rz]T為衛星位置矢量；v=[vx,vy,vz]T為衛星速度矢量；X=[rx,ry,rz,vx,vy,vz]T為衛星狀態矢量；w=[wx,wy,wz,wvx,wvy,wvz]T為系統噪聲；μ為地球引力常數；J2為帶諧項系數；Re為地球半徑;r為衛星到地心的距離。

2.2 自主定軌觀測方程

在太陽系質心(solar system barycenter,SSB)坐標系下，根據脈沖星導航的基本原理，可以得到脈沖星導航的基本測量方程[16]：

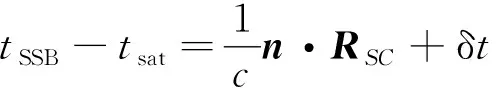
(3)

式中：tSSB和tsat為脈沖星同一脈沖到達SSB和衛星的時間；n為觀測脈沖星方向向量；RSC為衛星相對于SSB的位置矢量；c為光速；δt為星載原子時鐘偏差。

相較于脈沖星測距精度和觀測數目等因素，衛星鐘差對定軌精度的影響較小。不失一般性，針對本文開展的自主定軌研究，衛星鐘差忽略不計，并考慮地球、衛星和SSB三者位置關系，將式(3)改寫如下：

c·(tSSB-tsat)-n·RE=n·R

式中：RE為地球相對于SSB的位置矢量；R為衛星相對于地球質心的位置矢量。

在tk時刻衛星觀測1顆脈沖星時，測量方程可以表示為：

Zk=HkXk+Vk

(4)

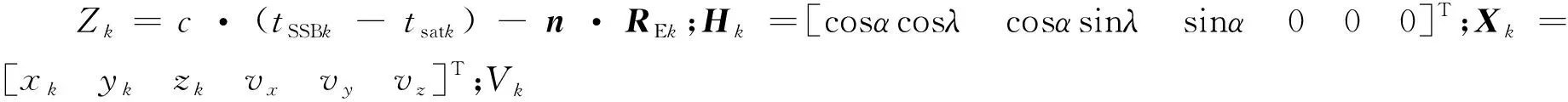
在X射線脈沖星定軌中決定定軌精度的主要因素是脈沖到達時間(TOA)的精度，TOA觀測量的測量噪聲方程可以估算為[17]：

(5)

式中：FB為X射線背景輻射流強；Fx為X射線輻射流強；tobs為信號觀測時間；P為脈沖周期；W為脈沖寬度；pf為脈沖調制度；Ae為探測器有效面積。

3 EKF算法及PWCS分析方法

標準卡爾曼濾波主要針對隨機離散線性系統模型，針對軌道動力學非線性的特性，采用EKF來解決隨機連續非線性系統問題。并在對系統進行濾波處理之前，用PWCS方法定性地分析系統狀態的可觀測性，這是反映濾波收斂精度和速度的重要指標。

3.1 EKF導航濾波算法

EKF的基本思想是將導航系統的狀態方程進行泰勒展開，忽視二階及二階以上的高階項，將展開式的一階線性項作為原狀態方程的近似表達式，再采用線性問題的標準卡爾曼濾波方法對近似的狀態量進行估計，從而得到最終狀態的次優近似值。

對式(2)和式(4)相應簡化后可以得到如下系統模型：

(6)

式中：t為時間參數；w(t)和v(t)分別為系統噪聲和觀測噪聲，且彼此不相關。

式中：δX(t)為兩者的狀態估計誤差。

進而得到誤差狀態的動力學方程為：

式中：F(t)為雅可比矩陣。進一步將狀態方程進行離散化處理，得到：

δXk=Φk,k-1δXk-1+Wk-1

(7)

式中：Φk,k-1=I+F(tk-1)·T，為k-1時刻到k時刻的狀態轉移陣；T為濾波周期。

由式(4)和式(7)可以建立系統的離散型線性干擾方程：

擴展卡爾曼濾波流程如下：

(1)濾波初始化

根據估計狀態信息，給出狀態變量及其相應誤差方差陣初始值：

(2)狀態更新

(3)量測更新

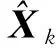
Pk=(I-KkHk)Pk/k-1(I-KkHk)T+

3.2 PWCS可觀測性分析方法

不論采用卡爾曼濾波或其他濾波方式，系統狀態變量的可觀測性是濾波收斂的前提條件。針對X射線脈沖星自主定軌系統是典型的非線性時變系統，提出基于分段式線性定常系統(PWCS)的可觀測度分析方法。在足夠小的時間區間內，可以忽略線性時變系統的系數矩陣變化，在該時間區間內就可以把時變系統近似為一個分段線性定常系統進行處理，這往往可以大大簡化分析過程。

離散型PWCS系統的一般形式為：

式中：j=1,2,…,q，為時變系統分段間隔序號。于是，系統總的可觀測性矩陣(TOM)可以表示為：

式中：

根據PWCS分析定理，如果系統滿足

null(Qj)?null(Φj), 1≤j≤q

則有

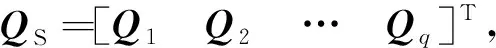
因此，可以用QS來代替QT分析系統的可觀測性，使問題得到簡化。又因系統狀態呈遞推關系，每個時間段的系統狀態初值就是前一時間段的系統狀態終值，則可觀測性矩陣仍具有累積繼承的性質。這樣可以用某時段j的可觀測性矩陣Qj進一步代替QS，使系統的可觀測性分析進一步簡化。

系統的可觀測矩陣Qj可以表示為：

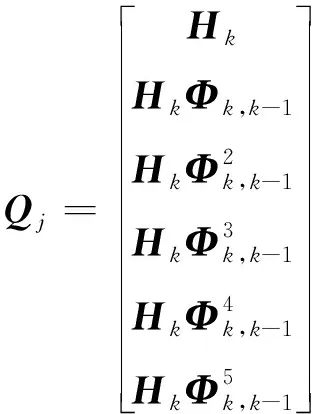
(8)

式中：

(9)

S中每個元素的量級為μ/r3，對于軌道高度為500 km的衛星，其數量級為10-6，近似為零，將式(9)其代入式(8)，并進行初等行變換，得到：

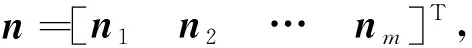
通過提取可觀測矩陣，進一步進行可觀測度的計算，用可觀測矩陣的條件數來對可觀測性進行量化，對Qj進行奇異值分解：

Qj=UΛVT

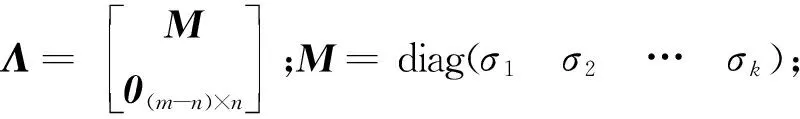
定義可觀測矩陣的條件數如下：

式中：σmax和σmin分別為M的最大奇異值和最小奇異值。矩陣的條件數η越大，說明矩陣越接近奇異。

系統可觀測性矩陣的條件數能夠反映系統狀態的可觀測程度，即系統可觀測性矩陣的條件數越大，系統的可觀測度越差。如果系統可觀測性矩陣的條件數是無窮大，則系統不可觀測；如果系統可觀測性矩陣的條件數等于1，系統的可觀測性最好。

4 數值分析試驗

4.1 XPNAV-1衛星的觀測數據分析

目前，XPNAV-1衛星仍正常在軌運行，對Crab脈沖星和3顆低流量IRP進行了詳細觀測，積累了大量觀測數據。從實測數據分析來看，掠入射式聚焦型探測器觀測的數據有較高的信噪比，因此在本文定軌算法研究中，主要利用該探測器采集的數據進行數值分析試驗。

自2016年11月18日以來，XPNAV-1衛星一直對Crab脈沖星進行重點觀測，除每年4月30日至8月1日期間Crab方向和太陽夾角小于45°，以及考慮與月球夾角小于5°不可觀測外，其余每天進行觀測，每個觀測弧段持續觀測時間為30～50 min。目前，通過累積觀測獲取了比較完整的Crab脈沖星觀測數據，并提取得到精化的脈沖輪廓，通過計時擬合建立了精度為55.14 μs的計時模型。

此外，該衛星在2017年2月21日至2017年8月31日，分別對3顆低流量IRP進行了長期觀測，每個軌道周期持續開展5～15 min低流量脈沖星探測，累積探測數據。經統計分析得到了3顆低流量IRP的流量統計以及能譜分析結果。但由于探測器有效面積較小，脈沖星光子流量較低，目前未能提取到低流量脈沖星完整的脈沖輪廓。

XPNAV-1衛星對Crab脈沖星的進行了完整的觀測。其中，時間跨度從2016年11月18日至2017年3月26日的觀測效果較好，共179段觀測數據，每個觀測弧段平均觀測時間約45 min。對該段實測數據做如下處理：1)在0.5～9.0 keV的能帶內選擇光子；2)篩除有效觀測時間短于40 min的觀測數據；3)篩除通量小于14個光子/s的觀測數據。最后從中選取時間跨度為30 d的數據用作數值試驗分析，共10組觀測值，其TOA誤差及相應的測距誤差如表2所示，實測數據的起止時間為2017年1月5日至2017年2月5日。

但是由于實測數據的信號積分時間較長，觀測量不充足以及測量序列不規則,所以僅僅只利用以上Crab的實測數據會導致濾波結果的發散。因此,基于Crab脈沖星實測數據的測距精度來模擬生成額外的觀測值，對30 d內的實測數據進行補充，對觀測周期進行壓縮，每500 s生成一個觀測值。

考慮到單顆脈沖星定軌系統的可觀測性差，再結合B0540-69，B1509-58，J1846-0258這3顆低流量IRP，利用1顆、2顆、3顆、4顆脈沖星的觀測數據組成數據組，分別進行軌道確定，分析觀測脈沖星數目對定軌精度的影響。利用Crab脈沖星實測數據，由Crab脈沖星觀測TOA與Crab脈沖星模型預報TOA的差，可以得到每個觀測時間段的TOA誤差(見表2)，計算得到TOA均方根誤差為99.05 μs，對應29.70 km的測距均方根誤差。由于3顆低流脈沖星光子流量較低，探測器有效面積較小，未能得到其完整的脈沖輪廓。由Crab脈沖星的完整觀測數據反算出背景噪聲，再根據3顆低流量脈沖星的實測光子流量統計以及探測器實際有效面積，利用式(5)的估計方程推算得到其測距精度，并由測距精度模擬生成觀測數據。表3給出了4顆脈沖星的赤經、赤緯和測距精度。

表2 基于Crab脈沖星觀測結果的TOA誤差及測距誤差

表3 4顆IRP的測距精度估計

4.2 顆脈沖星的可見性分析

在XPNAV-1衛星軌道覆蓋性分析過程中，影響其對目標脈沖星觀測的約束條件是：1)地球處于觀測目標與衛星之間，遮擋觀測信號；2)觀測目標與太陽之間的夾角小于45°，或者觀測目標與月球之間的夾角小于5°，高能粒子對探測器造成影響。XPNAV-1衛星的軌道周期約為94 min，圖1和圖2給出了4顆脈沖星在一個軌道周期內的可見性狀況。

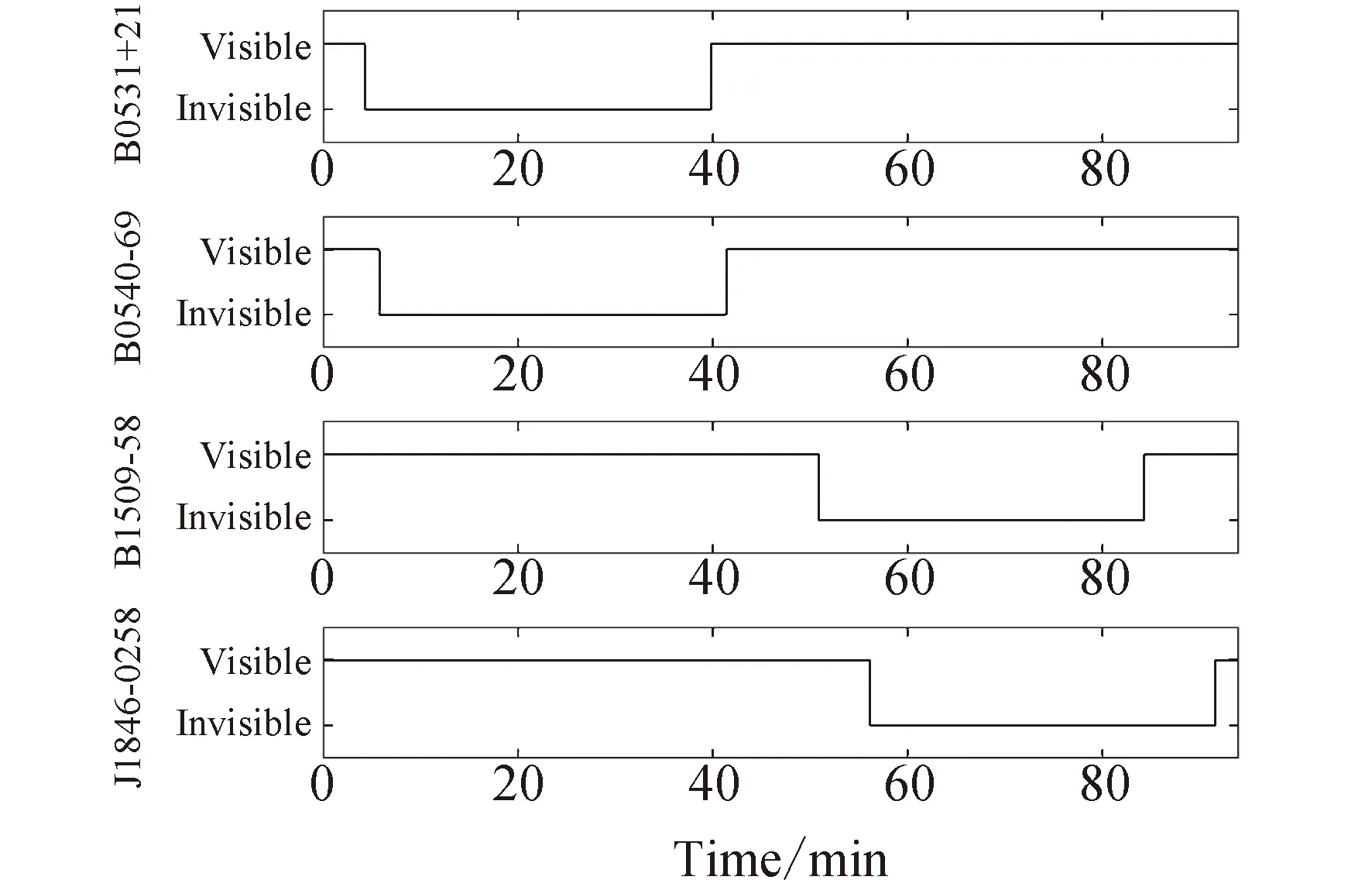
圖1 4顆脈沖星的可見性分析Fig.1 Visibility analysis of four pulsars

圖2 一個軌道周期內可見星個數Fig.2 Number of visible pulsars in an orbit period

由圖2可以看出，一個軌道周期內的任意時刻均最少有2顆脈沖星可被觀測到，脈沖星可見的時間百分比為100%，依靠4顆目標脈沖星的觀測信息，可以實現全時段定軌，從每個觀測弧段的可見星中選取單星進行導航，可以保證觀測信息的完備性。

4.3 濾波系統狀態可觀測性分析

系統可觀測度的數值試驗結果如圖3所示，縱坐標表示可觀測矩陣條件數，且取底數為10的對數。

表4給出了觀測不同脈沖星數目時，系統可觀測矩陣的條件數。當全程只觀測1顆或2顆脈沖星時，可觀測矩陣Qj條件數的數量級較大，矩陣接近奇異，定軌系統可觀測性差，無法實現濾波過程收斂。當觀測3顆脈沖星時，可觀測矩陣條件數明顯變小，系統可觀測度提高。當觀測4顆脈沖星時，可觀測矩陣Qj的條件數均值約為57，系統可觀測度較好，明顯優于前3組結果。可以總結出當觀測脈沖星數目增加時，可觀測矩陣條件數變小，系統可觀測度提高，數值試驗結果與上節理論分析結果一致。

圖3 基于4顆脈沖星的可觀測矩陣條件數Fig.3 Conditional number of observable matrix based on observing four pulsars

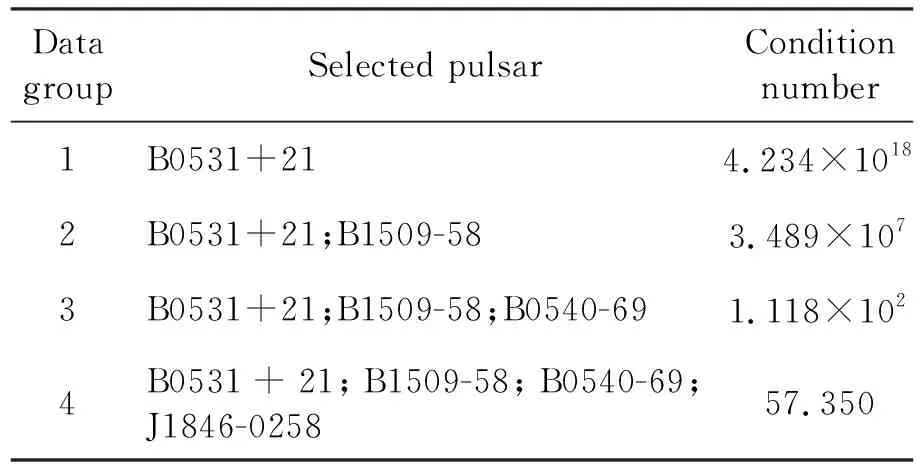
表4 脈沖星數量對系統可觀測度影響

4.4 自主定軌結果分析

利用第3組脈沖星數據組進行定軌計算，得到軌道誤差和速度誤差序列分別如圖4和圖5所示，進一步統計分析得到位置誤差均方根為56.65 km，速度誤差均方根為0.055 1 km/s。利用第4組脈沖星數據進行定軌計算的軌道誤差和速度誤差序列分別如圖6和圖7所示，進一步統計分析得到位置誤差均方根為40.24 km，速度誤差均方根為0.043 3 km/s。

圖4 基于觀測3顆脈沖星的軌道誤差Fig.4 Position error based on observing three pulsars

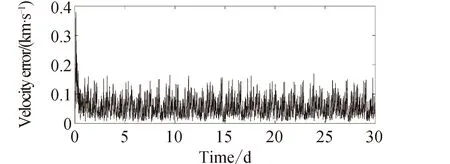
圖5 基于觀測3顆脈沖星的速度誤差Fig.5 Speed error based on observing three pulsars

圖6 基于觀測4顆脈沖星的軌道誤差Fig.6 Position error based on observing four pulsars

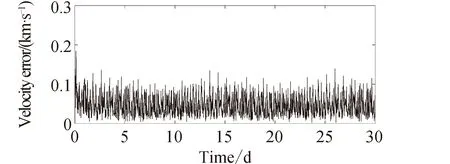
圖7 基于觀測4顆脈沖星的速度誤差Fig.7 Speed error based on observing four pulsars

由圖4～圖7可見，當觀測3顆或4顆脈沖星時，濾波過程收斂，并且隨著觀測脈沖星數目的增加，軌道誤差減小，定軌精度提高。

5 結束語

針對XPNAV-1衛星拓展試驗任務及脈沖星導航后續發展需求，利用多顆脈沖星實測數據，對EKF自主定軌算法進行數值試驗驗證。研究結果表明：當僅觀測1顆脈沖星時，系統的可觀測矩陣條件數極大，濾波結果很快發散；當觀測2顆脈沖星時，系統可觀測度提高，但條件數依然較大，濾波結果經過長時間依舊發散；當觀測3顆脈沖星時，系統可觀測度明顯提高，脈沖星對軌道完全覆蓋，濾波過程收斂，軌道確定精度為56.65 km；當觀測4顆脈沖星時，系統可觀測度進一步提高，脈沖星對軌道覆蓋性能好，濾波過程收斂，軌道確定精度為40.24 km；在所選脈沖星滿足該衛星整個軌道周期覆蓋的條件下，每個弧段僅需要觀測1顆脈沖星就可以進行定軌計算，其定軌精度取決于所選脈沖星的空間分布和數量。本文提出的EKF自主定軌算法過程收斂，試驗結果驗證了算法的合理性和有效性。EKF算法適用于線性高斯白噪聲的系統狀態估計，而實際的航天器軌道確定數學模型往往是非線性或非高斯的，存在線性化誤差、建模誤差和有色噪聲等問題。下一步將利用脈沖星實測數據，開展基于UKF、H∞濾波和粒子濾波等算法研究，對比分析各種算法性能，提出最優的定軌算法解決方案，為脈沖星導航算法研究和后續空間飛行試驗提供技術儲備。