一種基于工件偏轉(zhuǎn)的激光線掃描誤差補(bǔ)償方法*

張仁偉，孫晨晉，孫明浩，武 瓊，周志龍，于斌超，劉 巍

(大連理工大學(xué) 機(jī)械工程學(xué)院，遼寧 大連 116023)

隨著大型裝備制造的快速發(fā)展，加工目標(biāo)呈大尺寸、結(jié)構(gòu)復(fù)雜等趨勢，且局部小范圍區(qū)域內(nèi)精度要求高，因此，為保證局部區(qū)域的加工精度，必須實現(xiàn)局部小范圍的面形高精掃描[1-3]。線激光掃描技術(shù)具有精度高、方便快捷、測量速度快等優(yōu)點，在獲取零部件形位信息方面得到了廣泛應(yīng)用[4-6]。

激光線掃描儀可直接將零部件點云數(shù)據(jù)傳輸?shù)缴衔粰C(jī)，快速獲取所需的幾何特征。激光線掃描儀在采集復(fù)雜零件結(jié)構(gòu)時，存在儀器誤差、結(jié)構(gòu)本身誤差、安裝誤差和測量誤差等，導(dǎo)致測量精度低。因此，研究面向激光線掃描技術(shù)的誤差補(bǔ)償方法，理論與工程價值明顯[7-8]。安慰寧等[9]利用飛秒光頻梳頻域干涉的絕對測距方法，實現(xiàn)了激光線掃描儀的誤差校正和輸出控制。張亞等[10]分析了激光掃描技術(shù)在三維重建中存在的儀器掃描誤差、數(shù)據(jù)拼接誤差等因素，為激光掃描技術(shù)點云數(shù)據(jù)的處理和精度提高提供了重要參考。姚春榮等[11-12]通過線激光掃描方式，針對不同掃描速度下所采集的點云數(shù)據(jù)，提出了一種通過最小二乘法分區(qū)間建立誤差預(yù)測模型以實現(xiàn)誤差修正的新方法。邾繼貴等[13]提出了基于激光線掃描傳感器和通用工業(yè)機(jī)器人的測量方法，實現(xiàn)了自由曲面物體形貌的高精高效獲取。郝春艷等[14]獲得了掃描補(bǔ)償系統(tǒng)中的多源誤差及其相互影響關(guān)系，構(gòu)建了誤差分析模型。

與上述研究不同，為了提高激光線掃描儀的測量精度，提出了一種基于工件偏轉(zhuǎn)角的光學(xué)誤差補(bǔ)償方法，以工件偏轉(zhuǎn)點為突破點，結(jié)合設(shè)備安裝位姿及待測目標(biāo)結(jié)構(gòu)特點，首先制定了目標(biāo)點云數(shù)據(jù)的提取方案，然后構(gòu)建了工件偏轉(zhuǎn)及安裝誤差的補(bǔ)償方法，有效提高了系統(tǒng)測量精度。

1 局部激光線掃描三角測量方法

局部激光線掃描三角測量方法屬于點式或線定向，物體表面上點的絕對距離由參考平面確定。該方法所獲得的距離為一維數(shù)據(jù)，測量過程中，首先將激光投射到待測目標(biāo)物表面，然后利用反光信息和運動特征，獲得運動輪廓的二維坐標(biāo)[15-17]。局部激光線掃描三角測量原理如圖1所示，采用激光二極管投射激光，感光片等敏感元器件接收發(fā)射光，最終實現(xiàn)光學(xué)信號的自輸出與解碼。

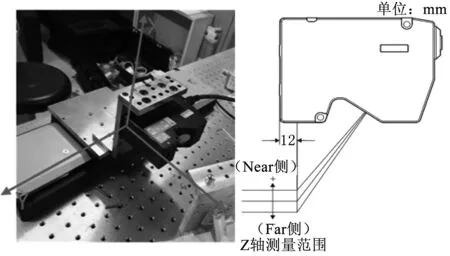
圖1 局部激光線掃描三角測量原理

激光入射光通過二極管發(fā)射，經(jīng)過透鏡組的折射之后，聚焦到被測目標(biāo)物體表面，發(fā)射回來的光通過濾鏡透鏡組，投射至線性半導(dǎo)體感光片陣列上實現(xiàn)數(shù)據(jù)傳輸。待測距離各異，光路結(jié)構(gòu)不同，因此反射光斑質(zhì)心位置亦存在差異，入射點到被測目標(biāo)物體表面的幾何參數(shù)可利用信號處理器的內(nèi)部幾何運算求得。

2 目標(biāo)數(shù)據(jù)預(yù)處理

被測件表面主要為曲率半徑較小的曲面和具有一定傾斜角度的斜面，采用激光線掃描儀局部測量系統(tǒng)可以實現(xiàn)對被測目標(biāo)的快速掃掠，進(jìn)而獲取其空間三維點云數(shù)據(jù)，然而，由于存在外界環(huán)境光干擾，導(dǎo)致相關(guān)點云數(shù)據(jù)存在粗差，如果將此類粗差數(shù)據(jù)直接用于后處理的補(bǔ)償和轉(zhuǎn)換計算，必然會嚴(yán)重影響數(shù)據(jù)精度。因此，基于Ransac算法，利用非線性誤差消除技術(shù)，實現(xiàn)點云數(shù)據(jù)的預(yù)處理。

提出了一種采用基于曲面特征的Ransac優(yōu)化模型，其原理如圖2所示。通過測量獲取的所有點云數(shù)據(jù)的集合記為N。首先，將點云集合N降為二維數(shù)據(jù)，然后獲得該分辨率下的曲線，記為集合n；逐個選取集合n中的曲線ni，然后抽取4組數(shù)據(jù)點，求解4組數(shù)據(jù)點的多項式矩陣k。進(jìn)一步，對ni中包含的數(shù)據(jù)點進(jìn)行{nii?Nii} 精度測試，若符合條件‖knii-Nii‖T0，則認(rèn)為該模型滿足了優(yōu)化要求。若不符合上述要求，需重復(fù)上述步驟，直至滿足最優(yōu)化模型。最終模型確立后，基于最小二乘優(yōu)化對所有的局內(nèi)點di進(jìn)行解算，從而獲得曲線模型，然后跳出循環(huán)，對于下一條曲線ni+1，重復(fù)上述步驟。

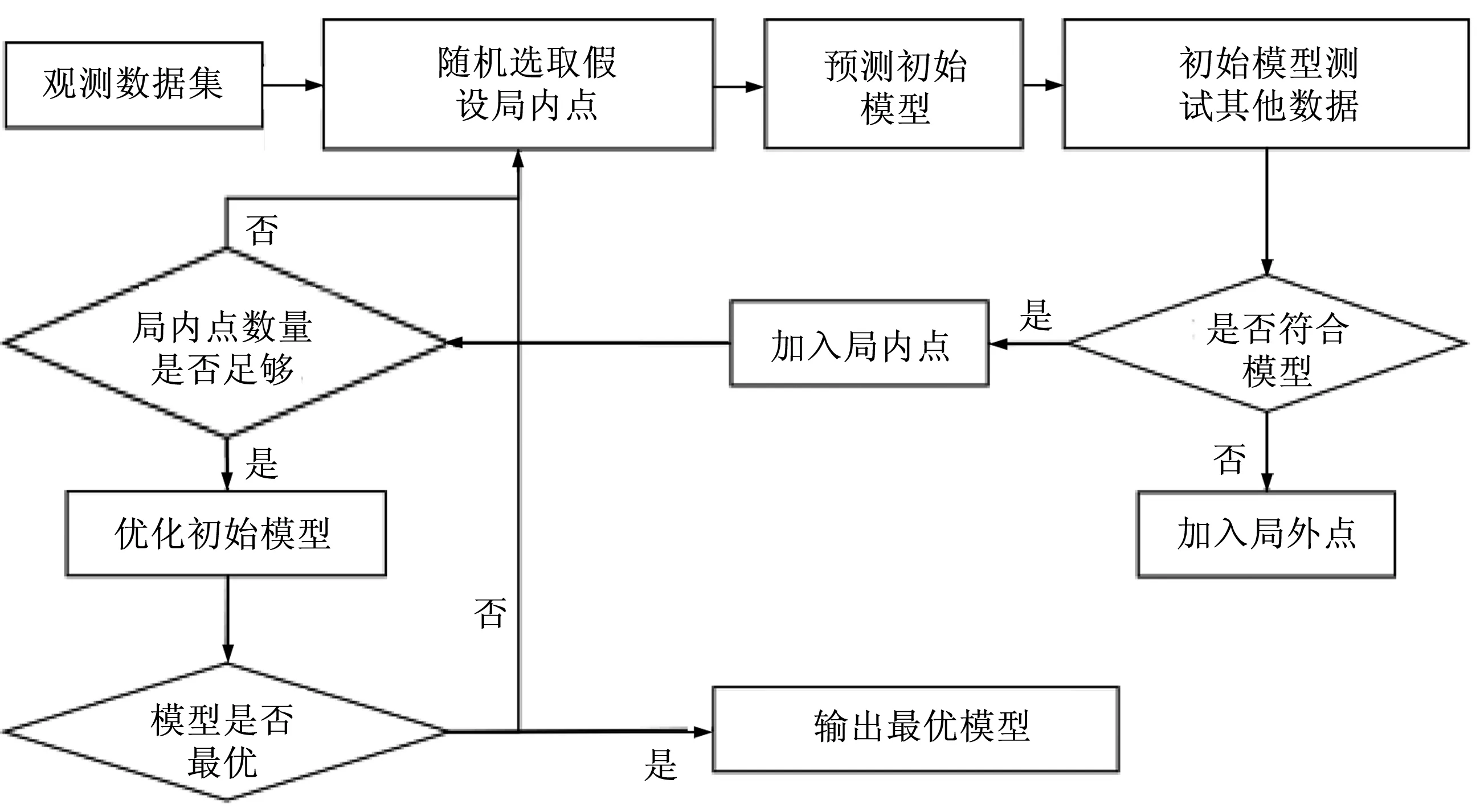
圖2 采用Ransac算法的參數(shù)獲取模型

3 基于工件偏轉(zhuǎn)的誤差補(bǔ)償方法

激光線掃描儀產(chǎn)生的入射光垂直投射到待測目標(biāo)物體后，在被測工件表面必將產(chǎn)生調(diào)制效應(yīng)，由于漫反射而產(chǎn)生空間散射場。透鏡聚焦的反射光線被內(nèi)部屏幕接收，獲得成像光斑，進(jìn)而輸出物體表面距離的數(shù)據(jù)信息，其變化由光能質(zhì)心位置所決定。激光線掃描三角測量方法的理論前提是入射激光成像點近似為精確點，實際測量曲面和傾斜面特征時，入射光與物體表面之間的夾角難以達(dá)到90°，光斑直徑較大，必然引入系統(tǒng)誤差，精度下降。

3.1 基于工件偏轉(zhuǎn)的光能分布

被測工件表面存在一定的曲率和傾斜，測量表面的偏轉(zhuǎn)導(dǎo)致結(jié)果失準(zhǔn)，在工件偏轉(zhuǎn)時三角測量方法需調(diào)整。假設(shè)工件實時偏轉(zhuǎn)角為γ，工件偏轉(zhuǎn)時的測量原理圖如圖3所示。

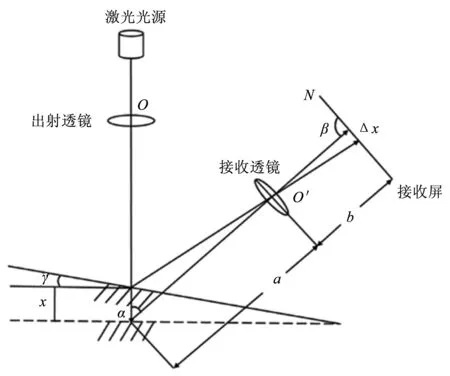
圖3 工件偏轉(zhuǎn)時的測量原理圖

在圖3中，入射光穿過出射透鏡O，在工件表面發(fā)生反射，反射光穿過接收透鏡O′聚焦于反射光接收屏上，x為工件的深度，Δx為對應(yīng)變化量。在工件傾斜時，準(zhǔn)確求解光能質(zhì)心位置，減少激光線掃描儀測量誤差。在測量階段，建立強(qiáng)針對性的非線性回歸模型，進(jìn)行三角測量光學(xué)評估，同時根據(jù)靈敏度分析參數(shù)變量。

漫反射時，在空間立體角度中，入射光線的輻射能量的分布滿足余弦變化關(guān)系

I(θ)=I0cosθ

(1)

式中，θ為目標(biāo)面法向與反射光線的夾角；I(θ)是反射光功率；I0為表面法向矢量方向下的角散射光功率。

設(shè)激光線掃描儀接收半徑為R，空間反射光場近似呈均勻分布，接收透鏡的光場能量E為：

(2)

式中，σ為入射立體角；a為原始被測工件特征點至接收透鏡中心的距離；ra為工件表面光點與接收透鏡光心的距離；α為入射、反射光線的夾角；β為反射光線與接收屏的夾角。

進(jìn)一步獲得接收透鏡的光場能量為

(3)

實現(xiàn)光能質(zhì)心的定位可減少激光線掃描儀的光學(xué)測量誤差。接下來，結(jié)合光場能量分布求解位移誤差，建立基于工件偏轉(zhuǎn)的誤差補(bǔ)償模型。

3.2 基于工件偏轉(zhuǎn)的誤差補(bǔ)償方法

基于光學(xué)幾何原理，對入射光進(jìn)行能量積分，當(dāng)光能中心線處兩側(cè)光能量積分相等時，關(guān)系表達(dá)式為

(4)

式中，x′為光能中心線在接收屏上的投射坐標(biāo)；φ為接收透鏡光場能量平分角。

φ的值可通過測量裝置內(nèi)部參數(shù)求解：

(5)

聯(lián)立式4～式5，得到平分投影點的坐標(biāo)為

(6)

工件偏轉(zhuǎn)角β初值為0，當(dāng)工件表面與入射光不垂直時，工件偏轉(zhuǎn)角β改變，即β≠0，此時接收屏上質(zhì)心位置偏移坐標(biāo)為

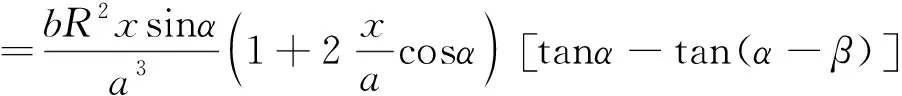
(7)

根據(jù)偏轉(zhuǎn)工件光學(xué)幾何關(guān)系，求解工件偏轉(zhuǎn)引起的距離偏差Δx為

(8)

實際測量過程中的誤差補(bǔ)償，需采用多組數(shù)據(jù)來提升補(bǔ)償?shù)木取Ｒ虼耍瑢⑵D(zhuǎn)角模型區(qū)域和誤差值組合，構(gòu)建多項式補(bǔ)償方法(見圖4)。

首先，根據(jù)被測工件實時偏轉(zhuǎn)角γ，基于裝置內(nèi)部幾何關(guān)系，可得到偏轉(zhuǎn)角模型關(guān)系表達(dá)式為

dt=tanγ-tan(anglefix-γ)

(9)

式中，anglefix為測量裝置內(nèi)部固定夾角，可通過實測結(jié)果和數(shù)模獲取數(shù)據(jù)差，然后分析模型原始數(shù)據(jù)對齊結(jié)果，計算每一測量段的角度對應(yīng)值：

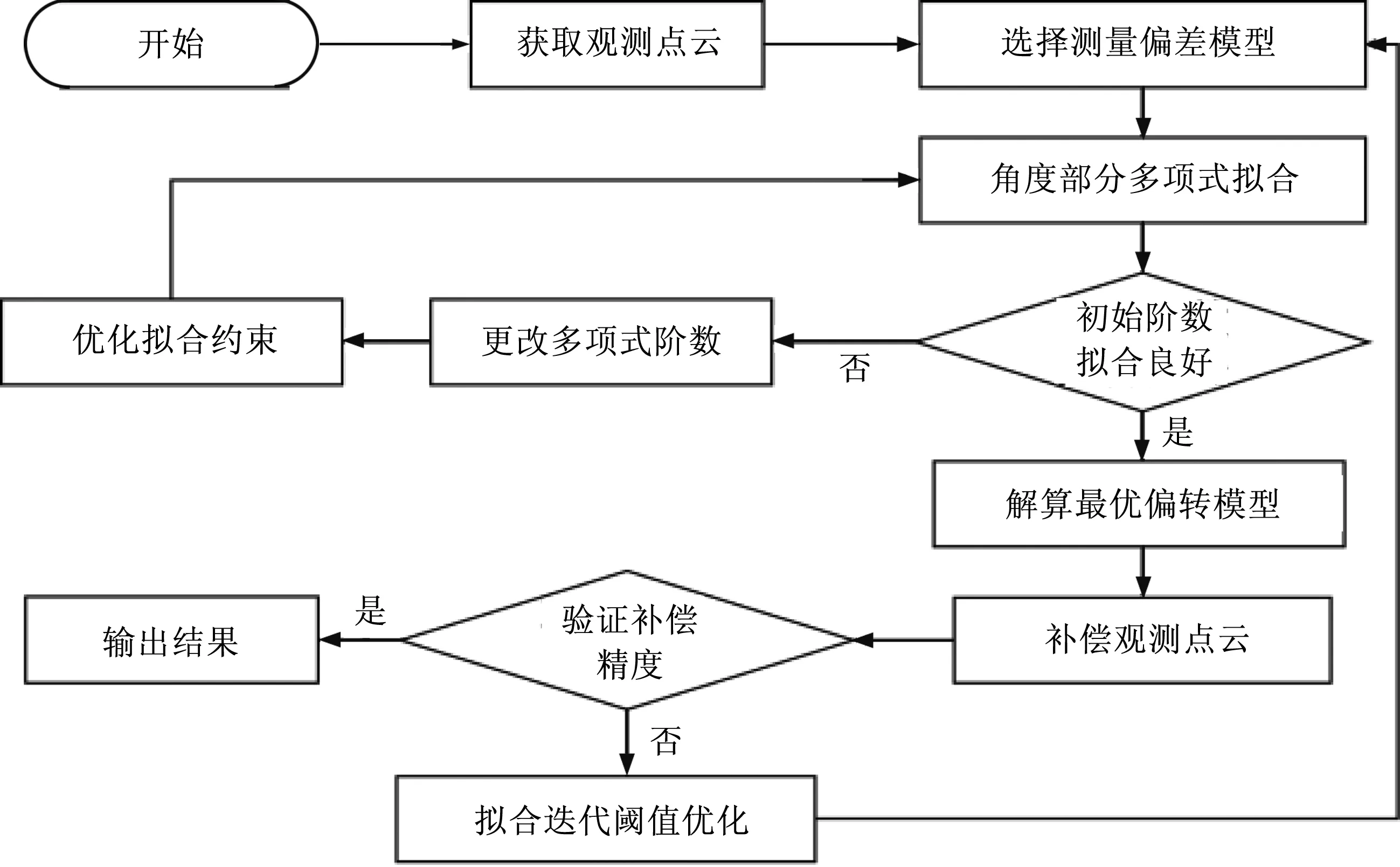
圖4 多項式補(bǔ)償方法流程圖

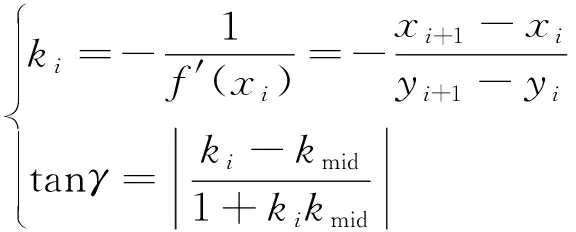
(10)

式中，ki為法向量；f′(xi)為原始數(shù)據(jù)曲線切向量；kmid為模型零偏移點法向量。

接下來，獲得全局參數(shù)的數(shù)據(jù)驗證模型ΔD為

ΔD=Hn.dt

(11)

式中，Hn為多項式變換矩陣，n為擬合項的階數(shù)。考慮到效率和實際應(yīng)用情況，一般選取5階以下多項式進(jìn)行數(shù)據(jù)擬合，選取大量先驗試驗數(shù)據(jù)，并進(jìn)行模型驗證，最終獲得對應(yīng)誤差補(bǔ)償模型及補(bǔ)償結(jié)果。

4 試驗驗證

為了驗證提出的基于工件偏轉(zhuǎn)角的激光線掃描誤差補(bǔ)償方法的有效性，首先采用三坐標(biāo)平面定位試驗來求解安裝定位初始偏差，同時通過提取非標(biāo)準(zhǔn)量塊和啞光陶瓷標(biāo)準(zhǔn)靶球的局部點云數(shù)據(jù)分別從定性、定量的角度分析工件偏轉(zhuǎn)誤差補(bǔ)償效果。試驗布局如圖5所示。

采用三坐標(biāo)測量夾具端面，完成平面定位，S型掃描點云得到夾具平面位姿信息。采用平面擬合法，求解對應(yīng)平面關(guān)系式。針對各個坐標(biāo)軸之間的位置關(guān)系，分別對實際情形下夾具坐標(biāo)系與平移臺理想坐標(biāo)系對應(yīng)角度的誤差矩陣進(jìn)行對比和驗證。此外，通過激光線掃描儀在工件表面投射激光并實現(xiàn)等步長掃描表面位置信息，對測量數(shù)據(jù)進(jìn)行重建與補(bǔ)償，從而提取優(yōu)化結(jié)果及模型真值，對比重建前后特征信息值的均方差。

基于Ransac方法，對曲面坐標(biāo)分層后進(jìn)行數(shù)據(jù)降維，剔除每條曲線對應(yīng)的坐標(biāo)誤差，最后得到最優(yōu)目標(biāo)數(shù)據(jù)，曲面掃描結(jié)果如圖6所示。

圖5 試驗布局圖

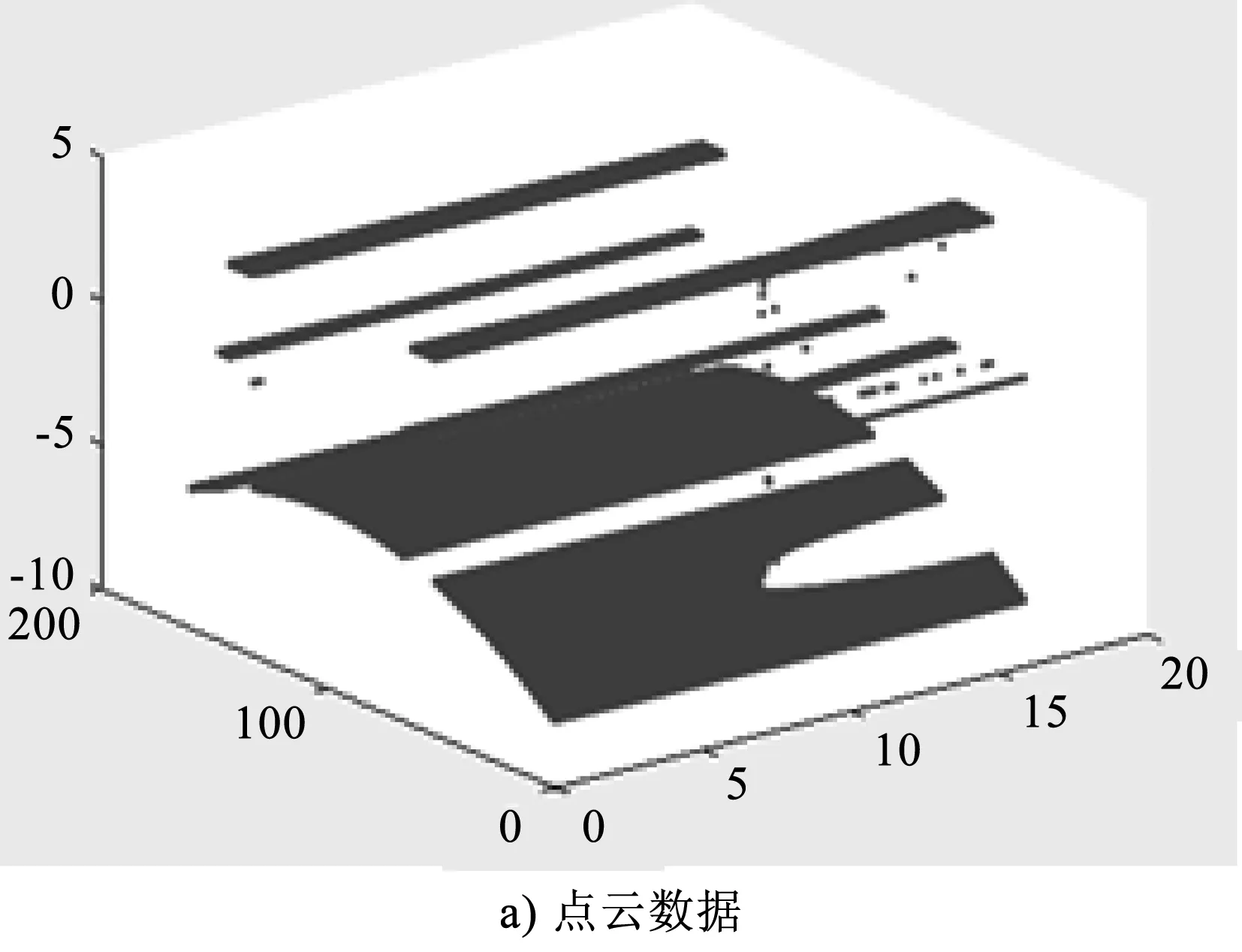
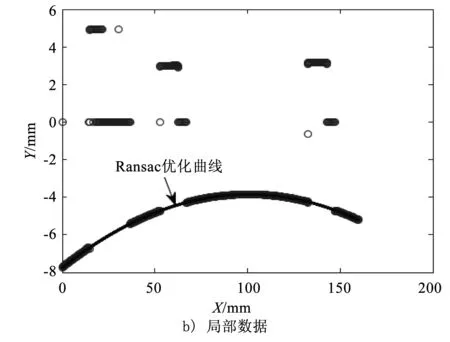
圖6 曲面掃描結(jié)果

基于所提出的工件偏轉(zhuǎn)誤差補(bǔ)償方法，設(shè)計試驗方案以驗證工件表面傾斜角誤差及補(bǔ)償模型的有效性。首先，將激光線掃描儀水平安裝在移動平臺上，確保入射光束方向的一致性，同時將標(biāo)準(zhǔn)靶球和非標(biāo)準(zhǔn)量塊固定在可升降平臺上。標(biāo)準(zhǔn)靶球直徑為25.385 mm，非標(biāo)準(zhǔn)量塊的曲率為1 305 mm。將位移平臺在零點時線掃描儀的測頭位置設(shè)為坐標(biāo)系起點，設(shè)置單軸運動采樣步長為0.02 mm，總測量距離為160 mm，共測量8 000列數(shù)據(jù)點，每一列包含800個數(shù)據(jù)點。將測量數(shù)據(jù)曲線與被測模型原始曲線進(jìn)行對比，對比結(jié)果如圖7所示。

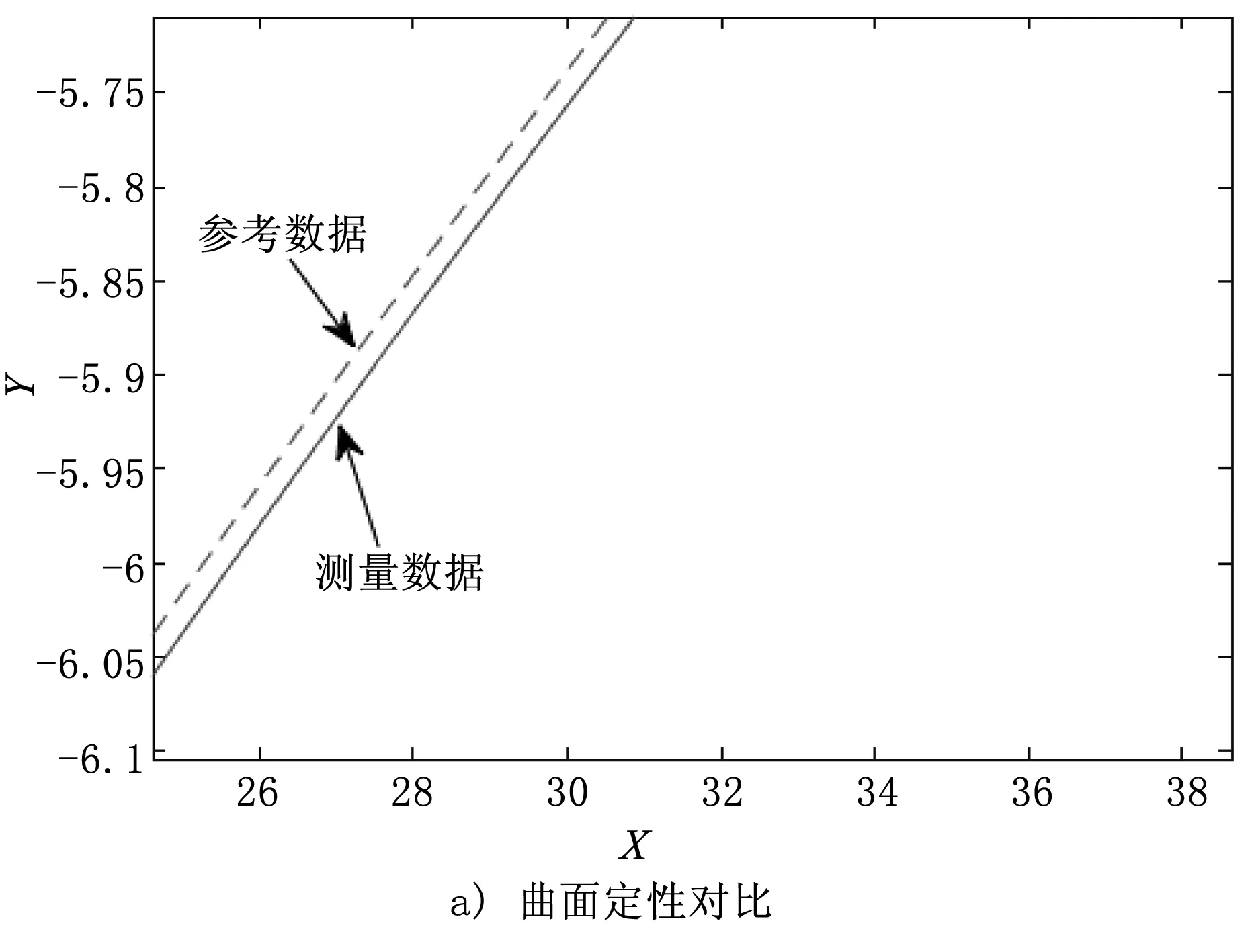
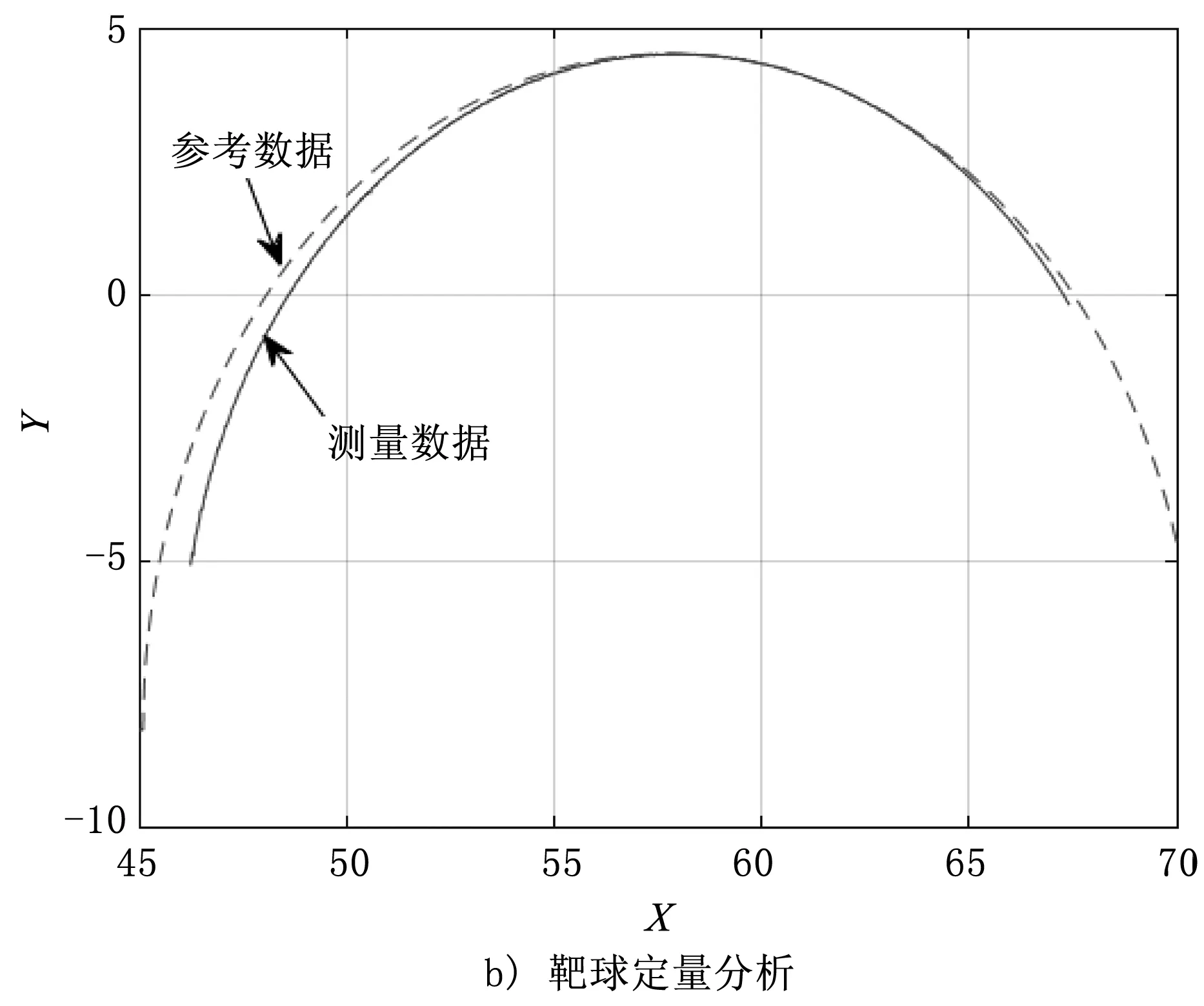
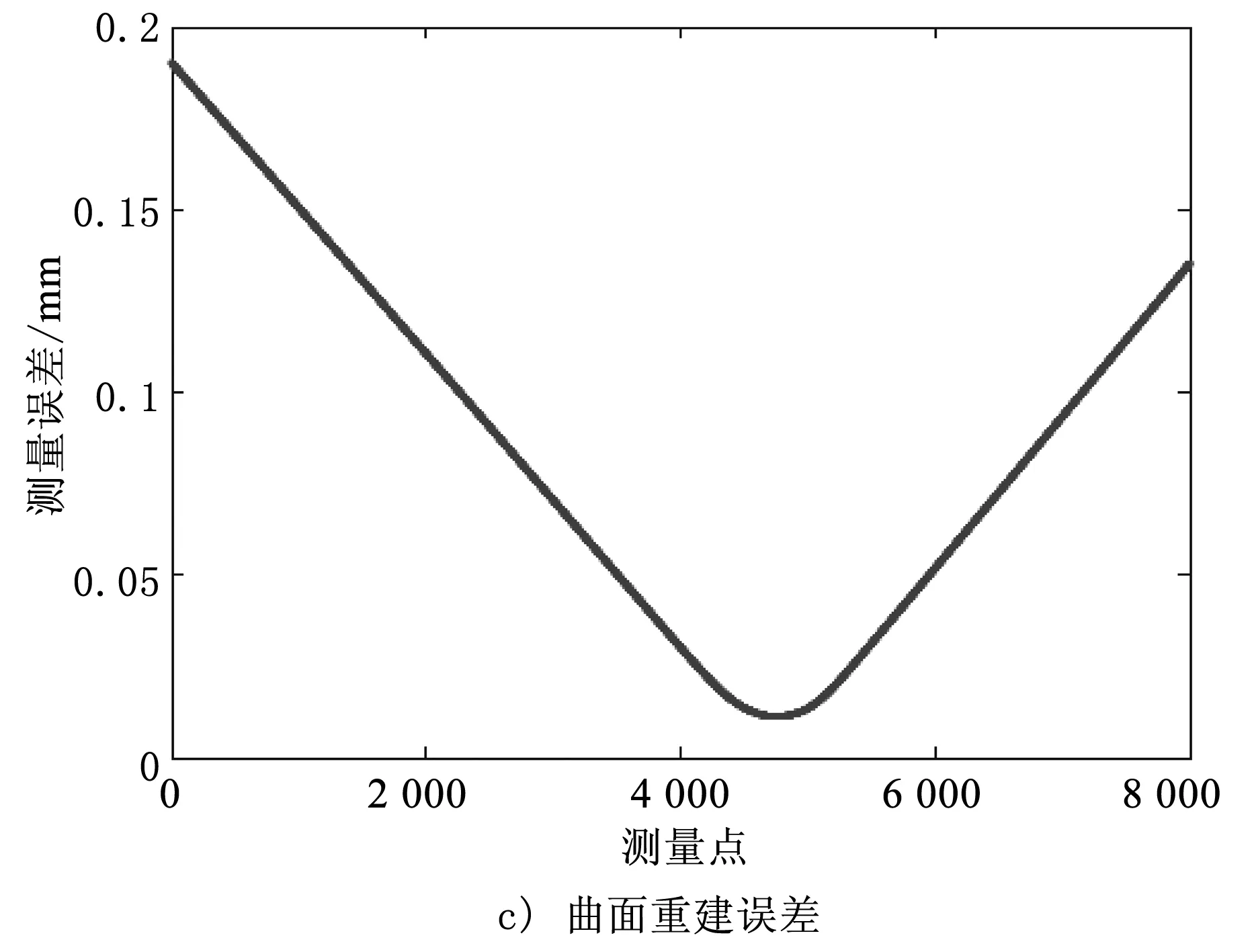
圖7 重建模型對比結(jié)果

基于多組測量數(shù)據(jù)的重建特征，求解曲面重建誤差的均方根值和6組靶球重建的補(bǔ)償結(jié)果，重建試驗對比結(jié)果如圖8所示。

由圖8可知，經(jīng)過補(bǔ)償后重建的測量曲線優(yōu)于原始測量曲線。經(jīng)過計算，補(bǔ)償后的靶球測量誤差減少了77%，擬合目標(biāo)半徑平均誤差均方根值低于10 μm，補(bǔ)償后的曲面測量誤差平均降低了75%，均方差低于0.05，因此，所提出的補(bǔ)償方法可有效降低測量誤差。

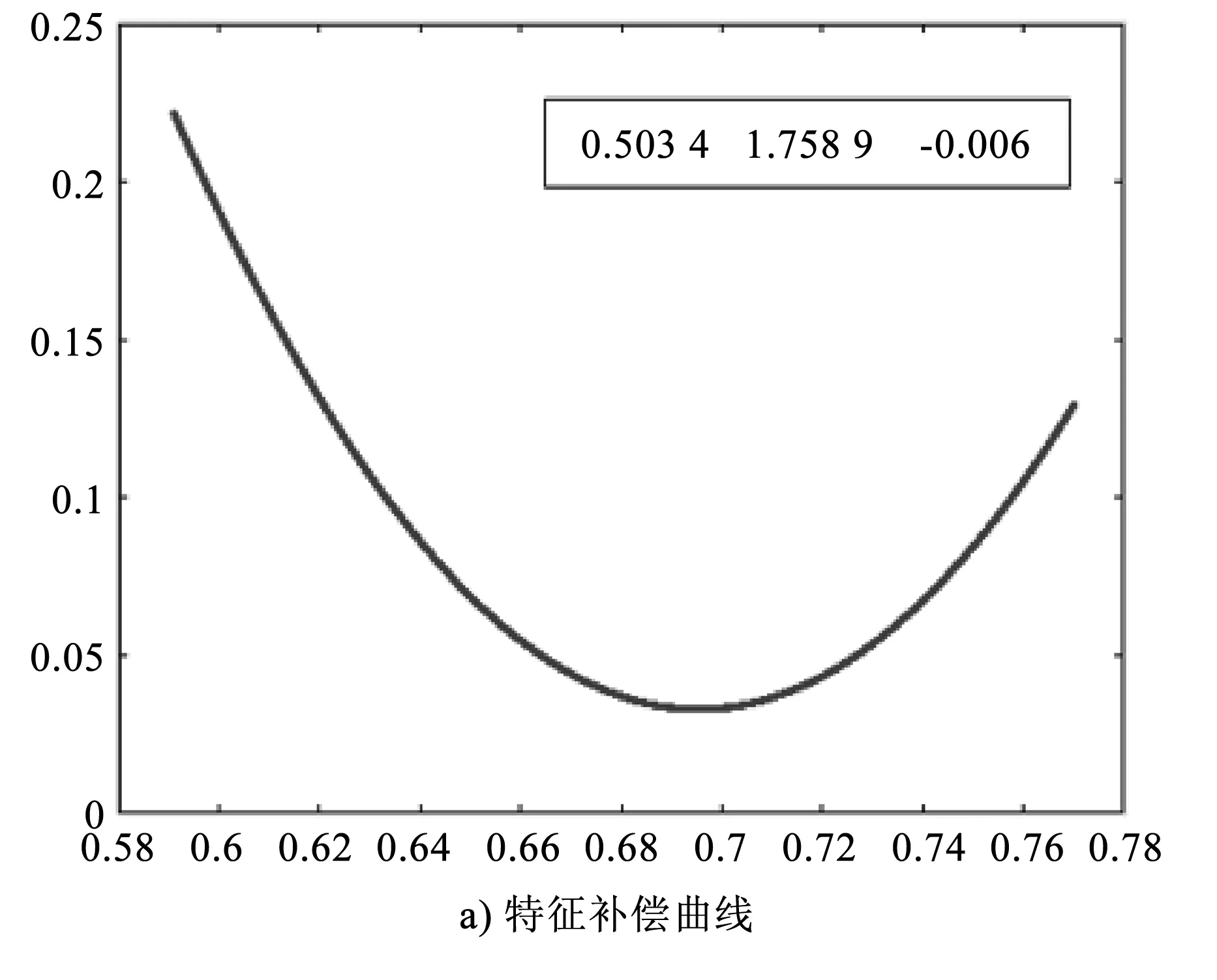
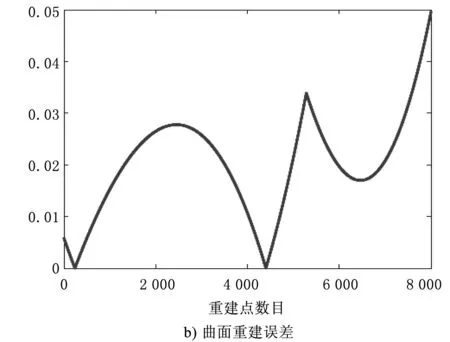
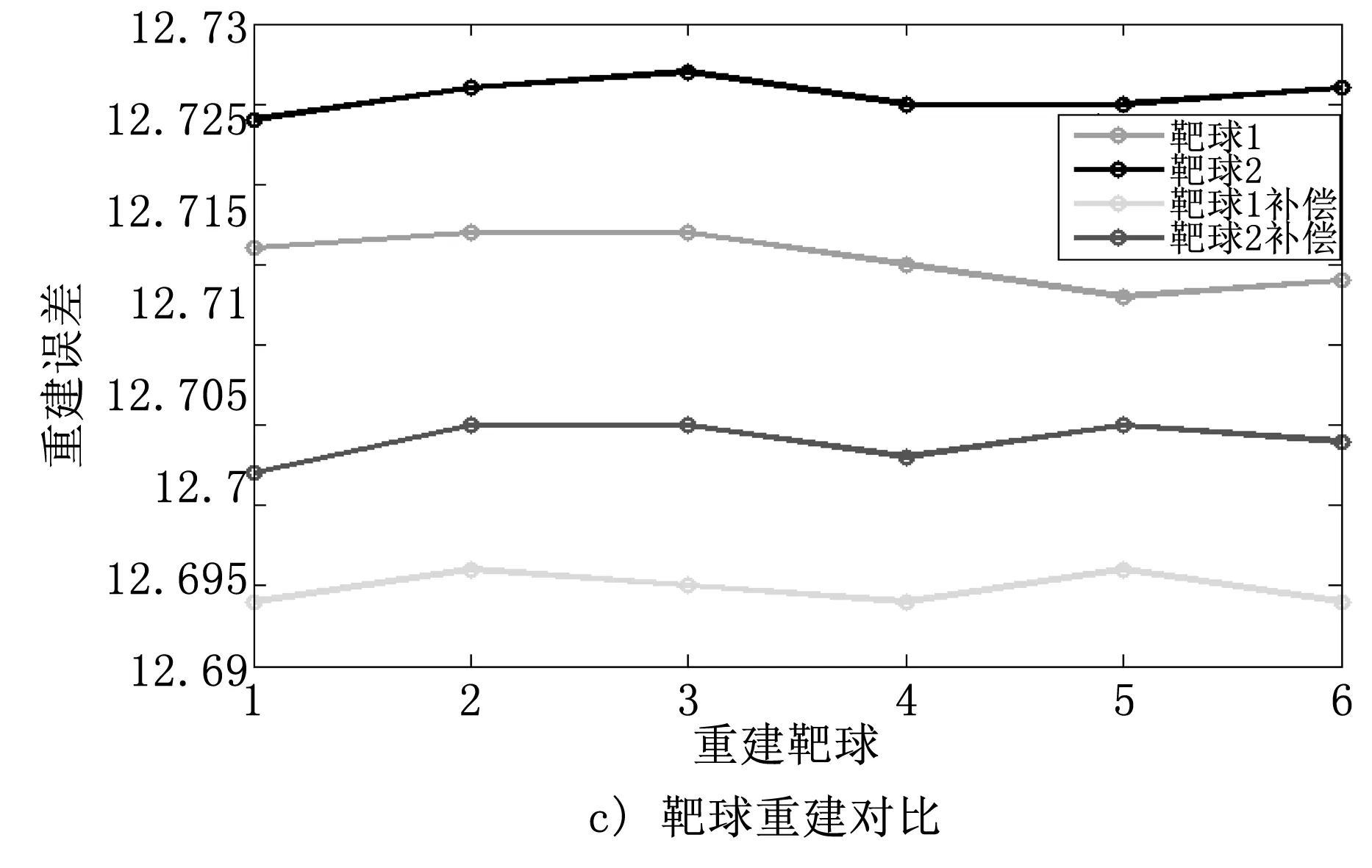
圖8 重建試驗對比結(jié)果

5 結(jié)語

所提出的局部三維坐標(biāo)測量方法，通過Ransac數(shù)值優(yōu)化獲取滿足局內(nèi)要求的特征點云，針對存在的系統(tǒng)誤差情況，提出了基于工件偏轉(zhuǎn)角的激光線掃描誤差補(bǔ)償方法，采用安裝角和數(shù)模配準(zhǔn)，對誤差進(jìn)行了溯源和優(yōu)化。該補(bǔ)償方法計算效率高，能夠?qū)崿F(xiàn)大批量點云數(shù)據(jù)的快速精確補(bǔ)償，同時，針對標(biāo)準(zhǔn)靶球和非標(biāo)準(zhǔn)量塊表面特征開展了多組提取試驗，結(jié)果表明具有較好的誤差補(bǔ)償效果。