基于外部載荷位置預測的光纖傳感器故障信號識別技術?

李顏瑞唐婧壹

(山西機電職業技術學院信息工程系，山西 長治 046011)

近年來，各項先進技術的發展，帶動傳感器技術也越來越成熟，在多個領域都起到了非常重要的作用，例如醫藥行業、工業、軍事領域等領域。 光纖傳感器在運行過程中可能會出現一些故障影響傳感器的正常工作，此時需要有相應的故障信號識別技術以解決這個問題。 現有研究的重點放在當傳感器出現故障時，怎樣才能快速、高效、準確地識別出傳感器故障信號位置，例如:文獻[1]提出了一種基于功率譜估計的兩級振動模式識別方案。 設計并實現了該算法的監控系統軟件，以及軟件系統設計中涉及的功能模塊。 對整個系統的實驗測試表明，該算法能夠實時有效地識別傳感電纜上的任何入侵事件，入侵檢測率大于95%，包括誤報。 但是該方法分析樣本數量較少，不具有廣義代表性；文獻[2]結合深度置信網絡和拉普拉斯映射法，實現了半監督故障的精準識別。 通過選取相應故障信號，將其轉換為低維流形特征的形式代入到深度置信網絡中，以此獲得少數的有標簽樣本和大量的無標簽樣本，分別提取特征并對故障類型做分類處理；然后，代入建立的識別模型中實現故障識別。 該方法降低了計算難度，較好地挖掘了故障信號特征，但是并未對信號進行去噪處理，影響算法整體識別精度。

光纖傳感器與其他傳感器相比，上市時間較短，對于故障識別方法的研究也相對較淺。 為此，本文從外部載荷位置預測的角度出發，提出了一種光纖傳感器故障信號識別方法。 首先，對傳感器信號中包含的噪聲和雜質采用合成外差算法和傅里葉變換分別進行解調和去噪處理，確保后續的特征提取結果精度；然后，針對不同故障類型分別提取了故障信號特征，將系統灰色性故障識別法與外部載荷位置預測法相結合，融合處理傳感器多角度負載數據，并進行故障識別。 在仿真分析中驗證了本文方法不僅在識別精度上有明顯的優勢，同時保證了理想的識別效率。

1 光纖傳感器故障信號分析

1.1 光纖傳感器故障信號解調去噪

光纖傳感器信號解調過程如圖1 所示。 本文將合成外差算法引入算法中，把相位調制信號代入傳感器信號中，使對傳感器信號產生影響的因素指向調制信號[3]。 為了有效去除傳感器信號中的噪聲，本文將分離傳感器信號與低頻干擾信號的頻帶，使敏感信號的偏振態變化和幅度波動處于較為平穩的狀態[4]。

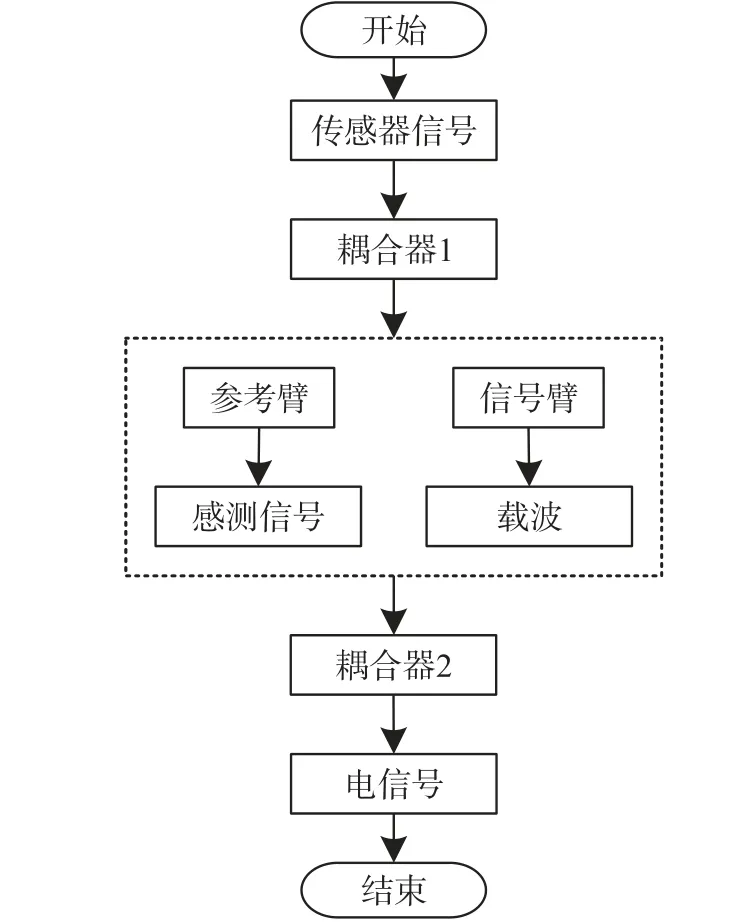
圖1 光纖傳感器信號解調過程圖

由圖1 可知，信號從傳感器中發出，經過耦合器1 的作用形成兩束不同的信號:感測信號和載波。由于傳感器信號中物理量的存在，參考臂使得感測信號產生物理反應，信號臂相位同時也受到一定程度的影響。 經過耦合器2 的作用使兩束信號匯合在一起，產生干涉現象，傳感器信號由此轉換為電信號，輸出即可。 輸出的電信號可用式(1)表示:

從式(2)中可得，當傳感器信號正好處于調制信號的邊帶上時，可通過載波頻率為整數倍的頻帶[5]對其進行過濾處理，過濾選擇的濾波器為中心頻帶ωc和2ωc的帶通濾波器，以此獲得傳感器信號向量S1(v)和S2(v)分別為:

再對S(v)進行積分計算，得到解調后的傳感器信號為:

式中:a表示經過伸縮處理后得到的伸縮因子，b表示經過平移處理后得到的平移因子，t表示一個常數量。

1.2 光纖傳感器故障信號特征提取

傳感器故障類型多種多樣，當傳感器出現不同故障時，為了可以準確判斷為哪種故障，本文分別提取了不同故障類型的特征[7]。 首先獲取傳感器運行信號，經過經驗模態分解技術的處理后，得到信號的本征模函數。 在本征模函數分量(IMF)中包含兩個部分:一部分為傳感器狀態信息，另一部分為傳感器運行狀態下產生的擾動分量。 然后，計算IMF 與傳感器信號之間的近似性，本文選擇關系值來表征，二者的關系值越大，說明IMF 中包含的傳感器狀態信息就越多。 IMF 與傳感器信號x(x＝1，2，…，N)之間的關系值計算公式為:

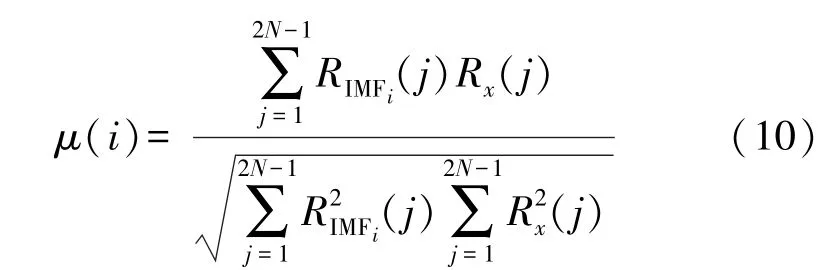
式中:RIMFi表示第i個IMF 的關系函數值，Rx表示x的相關函數值，j表示x的系數值。

選取兩個隨機變量X、Y，假設二者之間存在某種關系上的相關性，通過互信息[8－9]的非線性度量法來衡量兩個變量之間的近似性。 在X已知的情況下，條件熵H(Y｜X)與無條件熵H(Y)之間的關系為H(Y｜X)≤H(Y)。 那么，X、Y之間的互信息計算公式如式(11)所示:

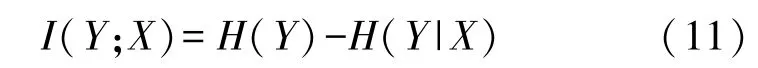
經過上述計算，篩選出IMF 中包含的敏感分量，通過對單個敏感分量進行分析，計算其與傳感器信號之間的互信息值和關系值，并將所得結果進行絕對值計算，得到絕對值后，以乘積的方式計算得到經驗模態分量的敏感度劃分標準。

由于傳感器狀態信息多為高維特征向量，運行狀態下會產生過多的冗余信息，使得特征提取效率降低。 這里引入輕量級協議算法進行降維計算[10－11]。

假設信號樣本集為X＝[x1，x2，…，xn]，其中含有n個D維空間樣本信息，使其映射到低維空間內，由此得到的樣本矩陣為Z＝[z1，z2，…，zn]，zi＝(i＝1，2，…，n)表示一個d維向量(d?D)。 將Q定義為與Z對應的相似性矩陣。 計算Q中包含的元素qij為:

式中:WPCA表示經過PCA 子空間的映射后，得到的變換矩陣，WLPP表示經過PCA 子空間和輕量級協議算法的映射后，得到的變換矩陣[12]。

根據式(15)的計算結果，利用式(16)的線性模型進行故障信號特征向量的提取:

2 外部載荷位置預測下光纖傳感器故障信號識別

根據上文故障特征提取結果，結合系統灰色性故障識別方法和外部載荷位置預測，對傳感器進行多角度負載，記錄所得數據。 在此基礎上，將所有數據進行融合，并利用故障識別法識別數據中的故障數據，實現過程如下:

在不同的運行狀態下，傳感器信號的特征也有所不同，通過觀察這些特征的變化，即可實現對故障信號的識別。 假設yi＝(yi(1)，yi(2)，…，yi(l))表示已知的傳感器故障特征向量，xi＝(xi(1)，xi(2)，…，xi(l))表示已知的傳感器信號特征向量[13]。yi與xi在第l個特征向量處的差異性計算公式為:

式中:m表示傳感器已知故障特征量數量，s表示所觀察到的傳感器信號組數。

通過計算傳感器運行狀態與標準狀態之間貼近度值的大小，找出最大的值，作為評判傳感器故障信號的指標，至此實現于外部載荷位置預測的光纖傳感器故障信號識別技術研究。

3 仿真分析

3.1 測試環境

為了驗證所提方法在光纖傳感器故障信號識別方面是否合理有效，需要進行仿真分析驗證。 測試在VC＋＋平臺上完成，數據來自某光纖傳感器運行數據，選取了其中的600 組，存儲在SQL Server 2015數據庫內。 在進行測試之前，需要將傳感器故障信號特征向量y1，y2，…，yi，…，yk進行歸一化處理，將其歸納到[0，1]區間內，得到:

式中:ymax表示故障信號特征向量的最大值，ymin則為故障信號特征向量的最小值。

3.2 頻率響應分析

光纖傳感器在實際的使用過程中，隨著信號頻率的不斷增加，頻帶的寬度也出現了變化，如果不及時處理，極易發生混疊的現象，很難得到準確的信號，從而導致信號解調失敗。 在仿真分析中，通過運用本文方法對0.5 kHz 情況下傳感器信號的頻帶進行解調，分析結果如圖2 所示。

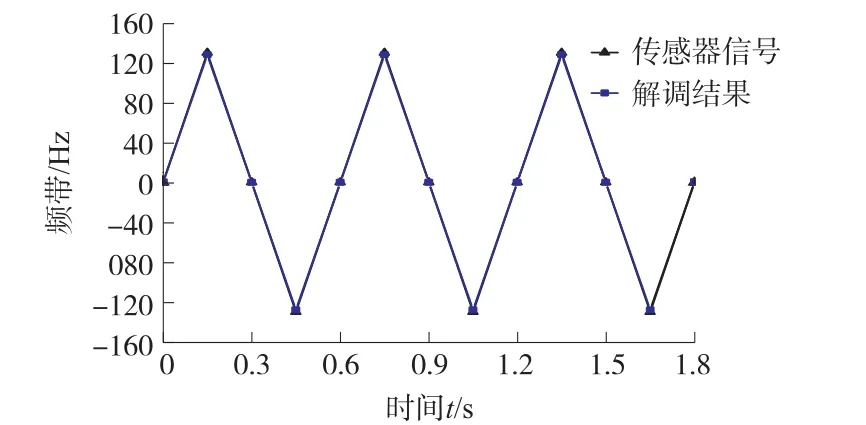
圖2 0.5 kHz 情況下解調傳感器信號結果

從圖2 中可以看出，在0.5 kHz 下，光纖傳感器波動在±140 Hz 內，且波動幅度較穩定。 通過本文方法的解調后，可以與原始傳感器信號始終保持在同一個變化幅度下，且波動范圍基本一致，沒有出現明顯波動，表明所提方法下調節手段能夠有效避免混疊現象，可以實現準確、實時的跟蹤解調，取得了理想的解調效果和頻率響應效果。

3.3 故障信號去噪分析

根據圖2 的解調結果，將其作為信號波動曲線，并提取解調過程中的2 100 個節點，分別利用本文方法與文獻[1]功率譜估計、文獻[2]深度置信網絡三種方法，對其進行去噪，驗證三種方法的信號去噪性能優勢，結果如圖3 所示。

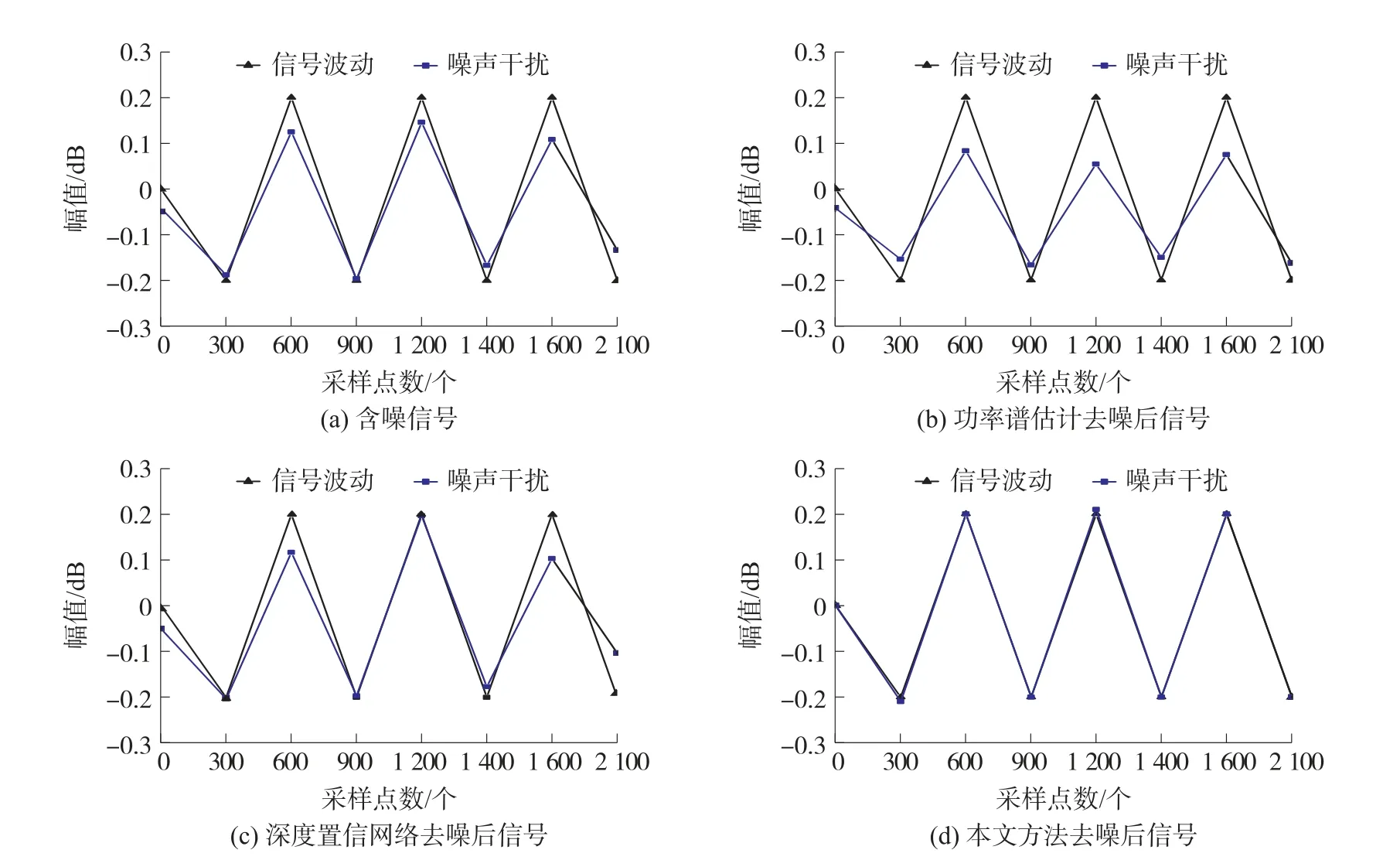
圖3 三種方法信號去噪對比圖

從圖3 中可以看出，經過功率譜估計和深度置信網絡去噪后的信號中，功率譜估計去噪后，噪聲幅值偏差相較于原始圖像噪聲偏差更大，深度置信網絡去噪后，去噪效果最好時為采樣點為1 200 個，但是依然存在一定程度的噪聲和雜質，并沒有達到理想去噪效果，對后續的故障信號特征提取在很大程度上都產生了影響。 但是經過本文方法處理后的信號，精準地去除了噪聲和雜質，噪聲干擾曲線與信號波動曲線之間存在的噪聲基本為0，在后續的故障信號特征提取以及信號識別中可以起到很好的推動作用。

3.4 故障信號識別效率分析

運用三種方法，分別對選取的600 組數據進行故障信號識別，所用時間如表1 所示。

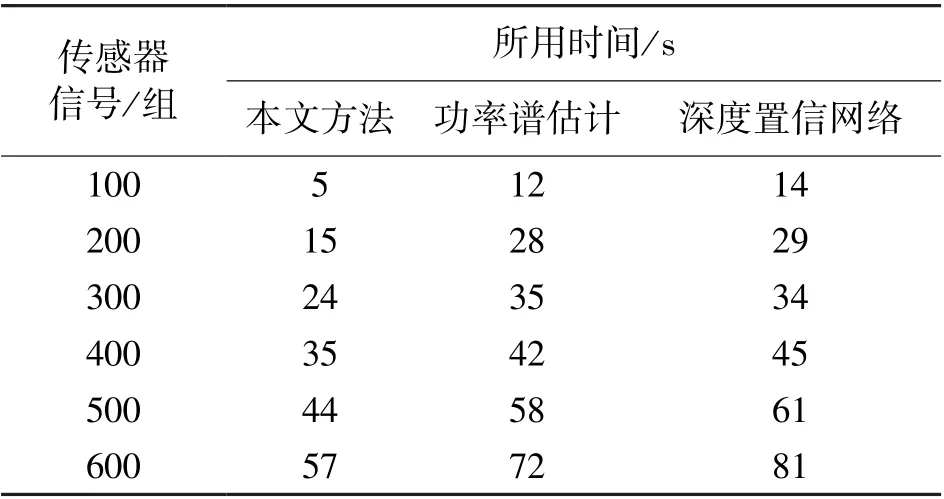
表1 三種方法下故障識別時間對比

從表1 中可以看出，三種方法隨著傳感器信號數量的增加、故障識別耗時都在不斷增加，但是對比之下，本文方法所用時間最少。 這是由于本文方法結合了系統灰色性故障識別方法和外部載荷位置預測，在數據融合之后對信號進行故障識別，在保證識別精度較高的前提下提高了識別效率。

4 實際驗證

為了進一步驗證所提方法的有效性，進行實際驗證，將某光纖傳感器的工作狀態劃為5 種，其中4種為故障，另1 種為正常狀態，分別為光纖鏈路故障、電機故障、光纖收發器故障、電源故障以及正常狀態，其樣本個數分別為20、20、35、25、100 個。 以此為基礎運用三種方法，分別對選取的樣本數據進行故障信號識別，所用時間如表2 所示。

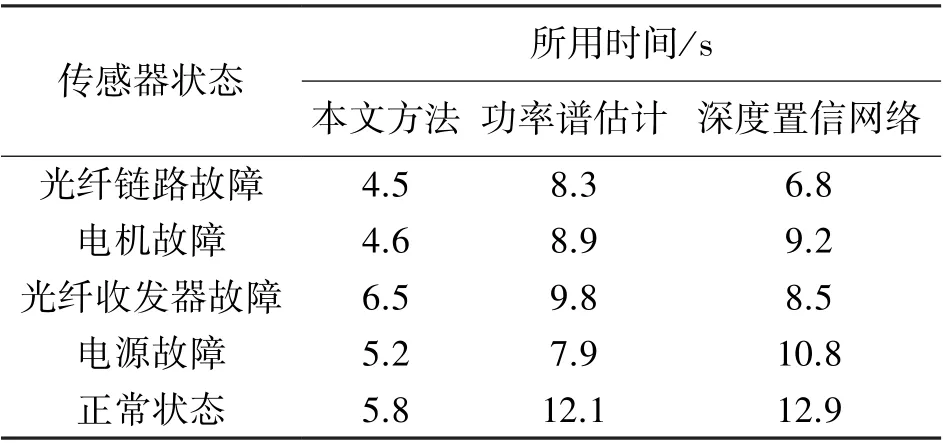
表2 三種方法下故障識別時間對比

從表2 中可以看出，本文光纖傳感器故障識別技術有效解決了當前光纖傳感器故障識別效率較低的缺陷，可以準確識別光纖傳感器的工作狀態。 相較于對比方法，所用時間在6.5 s 以內，識別效率和時間更高。 這是由于本文方法結合外部載荷位置預測方法，在數據融合識別光纖傳感器信號，準確分別故障信號類型，在保證識別精度較高的前提下提高了識別效率。

5 結論

當前針對光纖傳感器如何實現高效故障識別，本文提出了基于外部載荷預測的故障信號識別方法。 利用合成外差算法和傅里葉變換對傳感器信號中存在的噪聲和雜質進行解調和去噪處理，確保后續特征提取具有較高的精度，利用本征模函數對不同故障類型下的信號進行特征提取，結合系統灰色性故障識別方法和外部載荷位置預測，實現對光纖傳感器的故障識別。 仿真對比分析中，本文方法展現出了超高的識別效率，同時確保具有理想的識別精度，為傳感器技術的發展提供了可靠的參考依據。