基于遞推最小二乘法加速度計信息輔助的磁力計標定方法?

孫逸帆陳洋豪李 鳳徐 祥

(蘇州大學電子信息學院，江蘇 蘇州 215006)

隨著MEMS 技術的不斷發展，MEMS 磁力計有著廣泛的應用，通過磁力計可對地磁場進行測量，并計算得到姿態和航向信息。 但三軸磁強計的測量精度會隨著制作工藝等問題存在確定性誤差，例如標度因子誤差，零偏誤差，非正交性誤差。 此外，外界環境也會對磁力計測量精度帶來影響，包括軟磁材料引起的軟鐵干擾和硬磁材料引起的硬鐵干擾。 因此，為提高磁力計的測量精度，在使用磁力計前需進行標定[1－2]。

目前，國內外對磁標定問題進行了很多研究。 一種是姿態無關法，即不需要外部姿態信息作為參考，利用歸一化后的磁矢量輸出的模值為1，可對磁力計誤差參數進行標定。 在文獻[3－4]中，作者通過將磁矢量的輸出投射到一個橢球上，構建了磁力計的誤差參數與橢球參數的函數關系式，通過擬合橢球參數完成對磁力計誤差參數的估計。 為了進一步提高標定速度與精度，在文獻[5－6]中，作者通過模值標定法構建了關于磁力計誤差參數的代價函數，并通過遞推最小二乘法或列文伯格法對代價函數進行迭代運算進而完成標定。 為克服磁力計隨機噪聲的影響，在文獻[7－8]中，作者對隨機噪聲進行了考慮，構建了極大似然估計函數最優估計模型，并利用牛頓法對代價函數進行迭代求解。 對最優估計模型進行求解得到磁力計參數精度較高，但由于無外部參考信息，無法完成磁力計坐標系與慣性單元坐標系間未對準誤差估計，影響在實際應用中的精度。

另一種磁力計標定方法為姿態相關法，通過利用外部姿態信息，即陀螺輸出作為輔助，可對磁力計的誤差參數和磁力計與陀螺坐標系之間的未對準誤差進行標定[9－10]。 但在利用陀螺信息作為輔助時，首先要保證陀螺的精度。 對于陀螺標定，通常利用轉臺等設備，但這對MEMS 陀螺標定是昂貴的，且不滿足現場標定的實際情況。 因此，先對磁力計單獨標定，再使用加速度計信息作為輔助，對磁力計和磁力計與慣性單元間的未對準誤差進行標定的兩步標定法是近年來研究的主要方向。 在文獻[11－13]中，作者首先對加速度計和磁力計的誤差參數都采用極大似然估計法進行估計。 在完成傳感器的單獨標定后，再利用加速度計和磁力計間點積不變的性質，對磁力計和慣性單元間的未對準誤差進行估計。 在文獻[14]中，作者通過聯合標定的方法，將加速度計誤差，磁力計誤差和磁力計與慣性單元間的未對準誤差構建在一個代價函數中，通過對代價函數求解可得到誤差參數，但這一求解過程計算量較大，不適用于對計算量有要求的現場標定中。 在文獻[15－17]中，作者利用加速度計和磁力計點積不變的性質對磁力計的誤差參數和未對準誤差構建關系式，通過最小二乘法進行求解。但為標定準確，需采集足夠多的數據，計算效率低。

因此，本文提出一種基于遞推最小二乘法，利用加速度計信息輔助標定磁力計的方法，對磁力計誤差參數和磁力計與慣性單元間的未對準誤差進行一步標定。 首先，對加速度計進行標定。 再利用加速度計和磁力計間點積不變的性質，構建誤差參數模型。 最后，通過遞推最小二乘法，完成對磁力計誤差參數的參數識別。

1 相關工作與問題描述

1.1 MEMS 磁力計建模

常用的磁力計誤差模型為:

圖1 非正交性誤差示意圖

式中:dm＝－Rmb，nm＝－Rmε。

1.2 MEMS 磁力計標定的橢球擬合法分析

磁力計標定的姿態無關法為橢球擬合標定法，由地磁矢量的模值可得到:

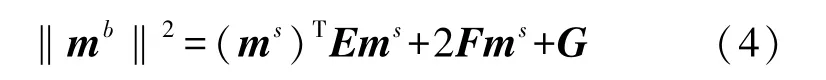
式中:E＝(Rm)TRm，F＝(dm)TRm，G＝(dm)Tdm。 由于存在測量誤差，磁力計的輸出矢量位于一個橢球面上，而橢球方程的系數是磁力計誤差參數的函數。 因此對磁力計誤差參數的估計可看做為橢球模型參數的估計。 在對參數Rm求解時，通常通過對E進行Cholesk 分解。 但由于無外部參考信息，因此分解不能得到唯一解。 例如，(Rm)T和Rm為一組解，(Rm)TQT和QRm為一組新的解。 其中Q為正交矩陣，代表標定得到的磁力計坐標系(b?系)與磁力計真實所在b系間的方向余弦矩陣。 圖2 表示磁力計在各個坐標系下三軸輸出的示意圖，實線代表磁力計在s系的三軸輸出，虛線代表磁力計在b?系的三軸輸出，半劃線代表磁力計在b系的三軸輸出。 如果沒有外部參考信息，則無法確定b系與b?系間的轉換關系。

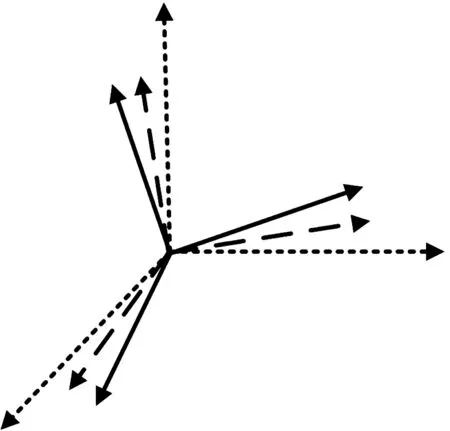
圖2 磁力計在s 系，b 系和b?系坐標系三軸輸出示意圖

因此，在只針對磁力計傳感器單獨進行標定時，不唯一解對標定結果沒有影響。 而在多傳感器的情況下，傳感器的誤差和傳感器間的未對準誤差的影響都不可忽略。 為消除這種影響，可通過加速度計的輸出作為輔助，完成磁力計與慣性單元間未對準誤差的標定。

1.3 MEMS 加速度計極大似然法標定

為實現加速度計輔助磁力計標定，首先應該對MEMS 加速度計進行標定處理。 MEMS 加速度計測量模型為:

對加速度計的標定，通常采用模值法。 但在標定過程中，存在隨機噪聲的二次項的數學期望不為零這一問題，因此傳統方法中標定加速度計過程中忽略隨機噪聲ε對誤差參數的估計屬于有偏估計。為消除隨機噪聲對標定結果的影響，構建極大似然估計模型:

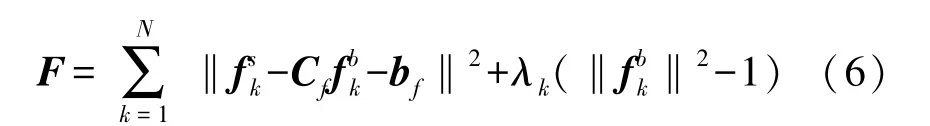
對極大似然函數模型(6)，通常采用牛頓法或梯度下降法，通過迭代計算估計出MEMS 加速度計的誤差參數。 為了保證迭代的準確性，需要對迭代的初始值進行估計。 迭代初始值的估計，可在式(5)中忽略噪聲ε的情況下，利用最小二乘法估計得到誤差參數。

2 加速度計輔助MEMS 磁力計標定方法

2.1 MEMS 加速度計極大似然法標定

因為地球上任一位置的重力矢量與地磁矢量間的夾角為固定值，磁傾角如圖3 中虛線所示角，磁傾角γ可表示為:

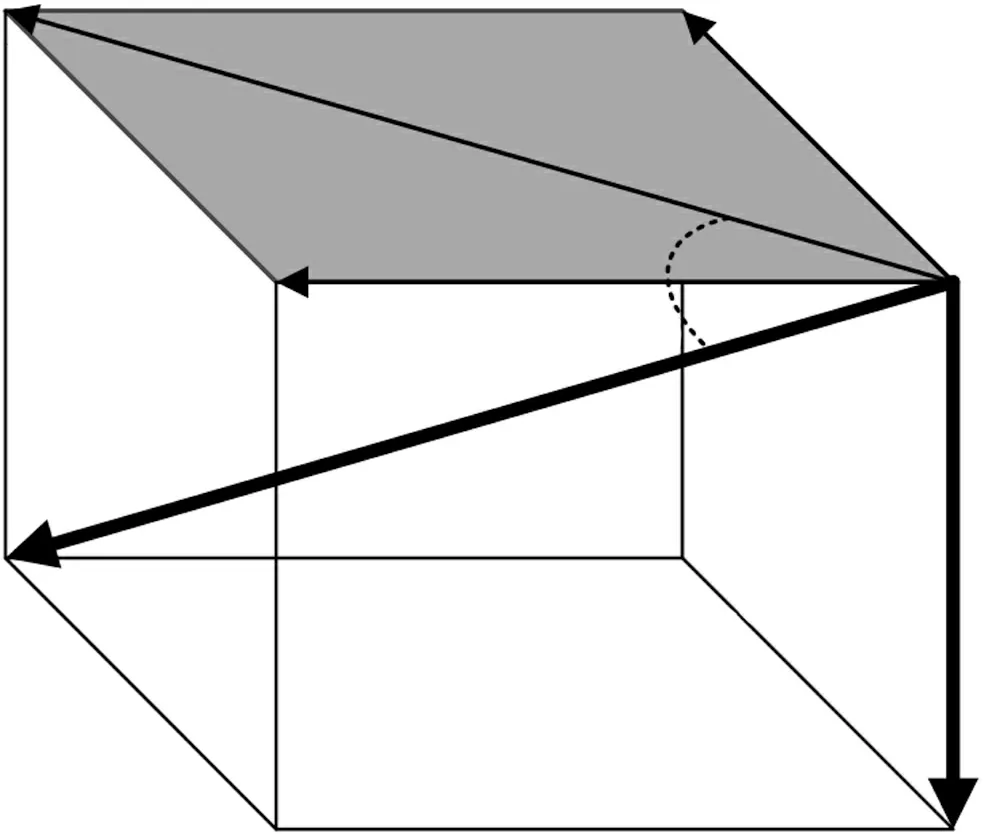
圖3 地球上任一位置矢量示意圖

式(10)為對MEMS 磁力計誤差參數的線性表達式，針對這個線性回歸問題，可以通過最小二乘法或其他方法進行解決，進而完成標定。 為減小計算量，提高效率，本文采用遞推最小二乘法對式(10)進行迭代求解。

2.2 遞推最小二乘參數識別法

由于標定是在地球上某個位置進行的，因此可認為磁傾角不發生改變，因此標定過程中的重力矢量與地磁矢量點積值為固定值，觀測方程可寫為:

式中:Kk表示k時刻的增益矩陣；Pk｜k－1表示k時刻一步預測狀態誤差協方差矩陣；Rk表示k時刻量測噪聲協方差矩陣；＾θk｜k表示k時刻誤差參數最優估計值；Pk｜k表示k時刻的誤差協方差矩陣；I9×9表示大小為9×9 的單位矩陣。 誤差協方差矩陣初始值設置如(16)所示，迭代參數的初始值設置為(17)所示:

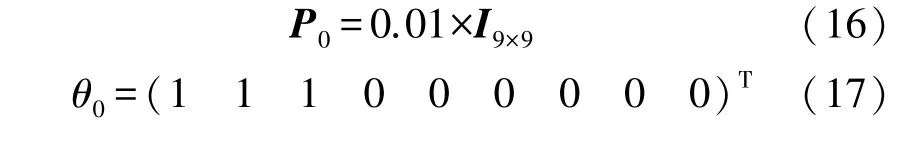
3 仿真和實驗

3.1 仿真部分

為驗證本文提出算法，仿真產生多位置MEMS加速度計與MEMS 磁力計數據。 設置數據采樣頻率為100 Hz。 根據MEMS 磁力計誤差模型式(2)，設置磁力計誤差參數如(18)，(19)所示。 MEMS 磁力計噪聲設定為均值為零，標準差為0.007 的高斯白噪聲。 仿真產生標定后的MEMS 加速度計數據，其隨機噪聲設定為均值為零，標準差為0.002 的高斯白噪聲。

仿真產生的50 s 數據通過本文提出的方法進行標定，圖4～圖6 為估計出的磁力計誤差參數迭代過程。 其中，虛線代表設定的磁力計參數，實線代表磁力計估計得到參數。 從圖中可看出，在5 s 左右，dm和Rm的估計值已經收斂到設定真值的附近。 觀察30 s～50 s 迭代過程中dm和Rm的估計值與設定真值間誤差，可看出誤差分別為10－3和10－4量級。 因此，可看出本文提出標定方法收斂速度快，收斂值準確。

圖4 MEMS 磁力計dm 估計值迭代過程圖

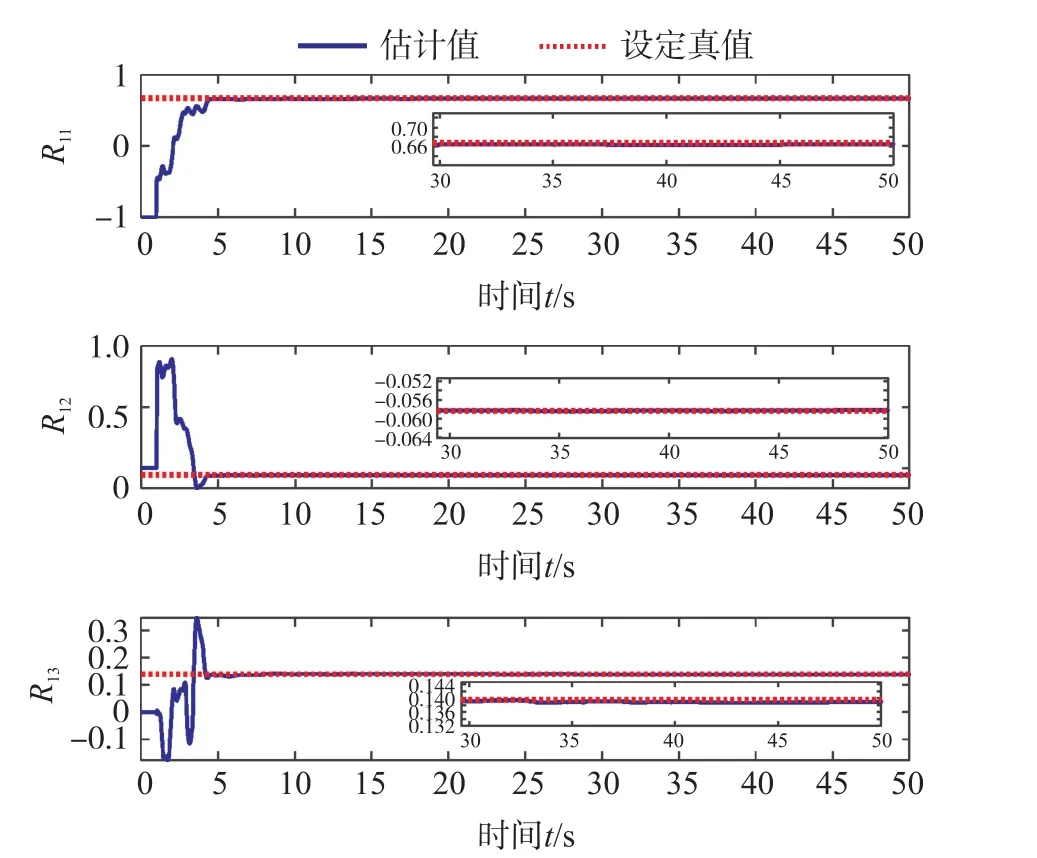
圖5 MEMS 磁力計Rm 估計值的模值迭代過程圖

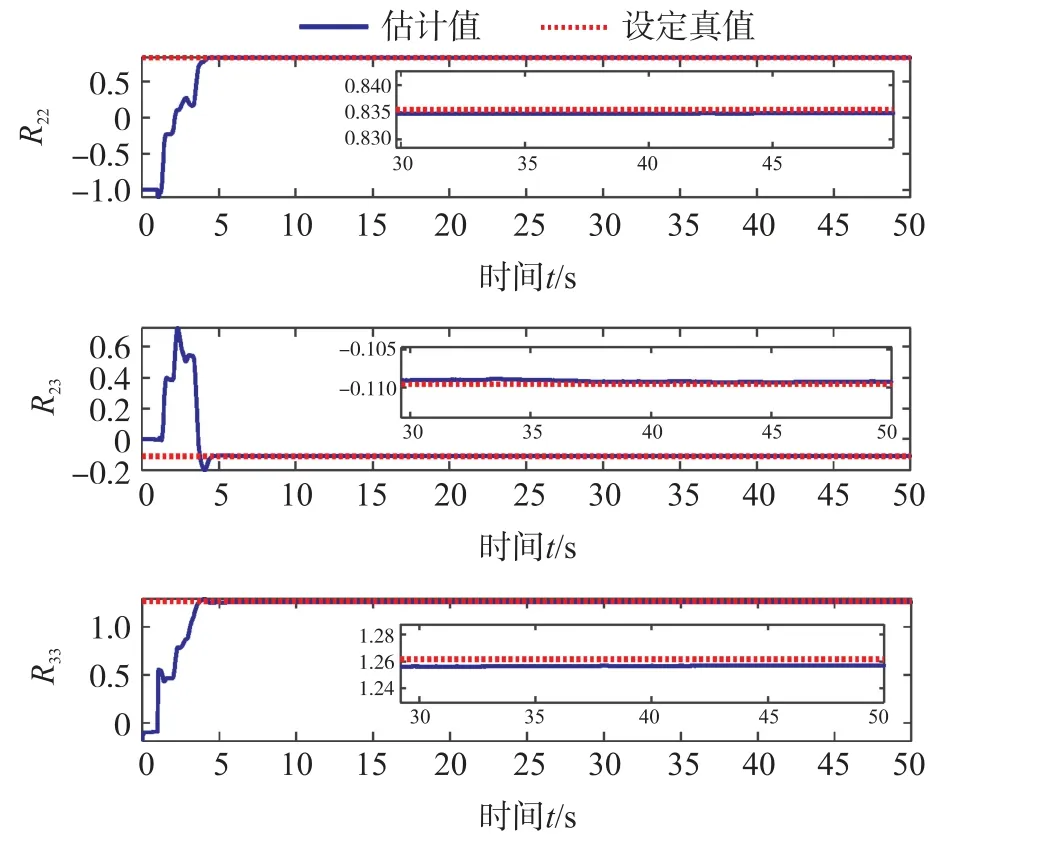
圖6 MEMS 磁力計Rm 估計值的模值迭代過程圖

圖7 中，將本文提出方法與橢球擬合法標定后的磁矢量模值進行比較。 其中，點劃線表示標定前磁矢量模值，實線表示橢球擬合法標定后磁矢量模值，虛線表示本文方法標定后磁矢量模值。 從圖中可看出，經過標定后，兩種方法的磁矢量模值都在1 附近波動。 經過橢球擬合法標定后的磁矢量模值平均值為0.999 8，標準差為0.004 7。 經過本文標定方法標定后的磁矢量模值平均值為0.998 4，標準差為0.004 8。從模值上看，兩種方法標定效果相似。 但本文提出方法是基于線性式(9)，因此，在標定過程中解決了加速度計與磁力計坐標系對準問題，克服了橢球擬合法中分解的不唯一解帶來的影響。 根據式(7)，可對加速度計矢量與兩種方法標定后的磁矢量間的旋轉角進行求解。 圖8 中，虛線表示橢球擬合法標定后矢量間旋轉角，實線表示本文方法標定后矢量間旋轉角。 仿真中設置的磁傾角為47.5°，從圖8 中可看出，橢球擬合法標定后矢量間旋轉角的曲線波動較大，其均值為47.48°，標準差為2.924。 而經本文方法標定后的矢量間旋轉角波動較小，其均值為47.52°，標準差為0.317。 因此，可認為本文在標定過程中穩定完成了對矢量間對準誤差的估計。

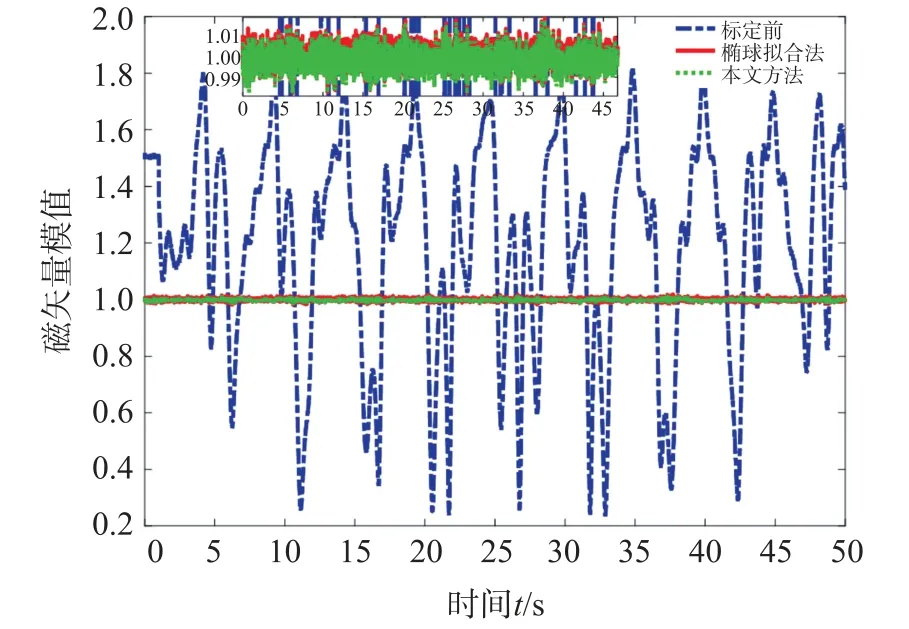
圖7 標定前后磁矢量模值比較圖

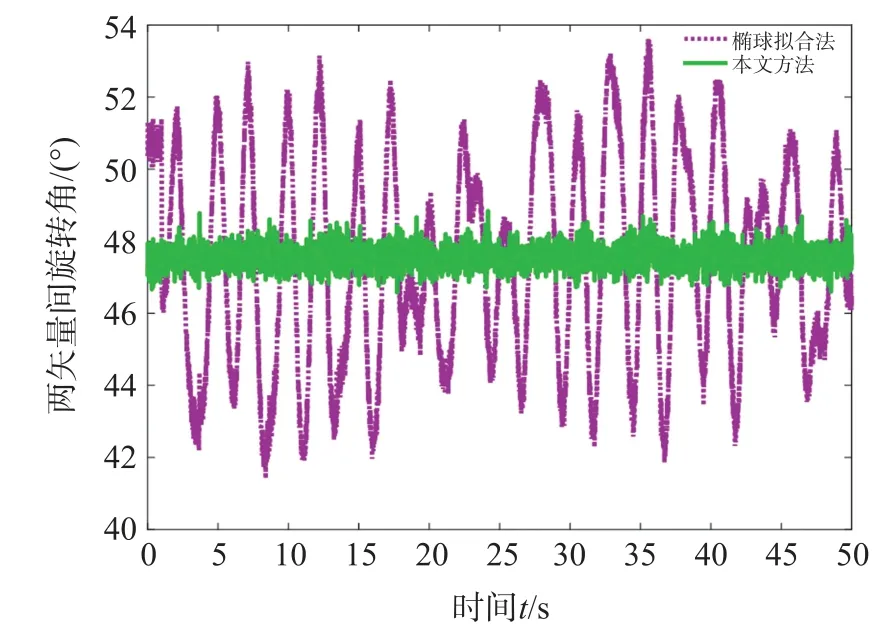
圖8 加速度計矢量與磁力計矢量間旋轉角

3.2 實驗部分

為采集實際數據對本文算法進行驗證，設計了硬件部分。 如圖9 所示，其中，STM32F407 作為主控芯片，對ICM20948 九軸MEMS 傳感器進行數據采集，通過串口將數據傳輸到上位機并存儲。 設置采樣頻率為100 Hz，對固定在無磁3D 打印的外殼中的硬件部分進行緩慢旋轉，采集100 s 磁力計與加速度計數據并存儲。

圖9 實驗實物示意圖

首先，對采集到的ICM20948 加速度計數據進行極大似然標定處理。 其次，利用磁力計和標定后的加速度數據，分別通過橢球擬合法和本文提出方法進行標定處理。 圖10 中，對標定前和經過兩種方法標定后的磁矢量模值進行了比較。 其中，用o 表示標定前磁矢量模值，用＋表示橢球擬合法標定后磁矢量模值，實線表示本文方法標定后磁矢量模值。從圖10 中可看出，本文方法標定后磁矢量模值曲線高于橢球擬合法模值曲線，且經過兩種方法標定后的磁矢量模值在1 附近波動。 其中，經過橢球擬合法標定后，磁矢量模值平均值為0.998 7，標準差為0.021。 經過本文方法標定后，磁矢量模值的平均值為1.012 7，標準差為0.021。 因此，可認為完成了磁力計的標定。

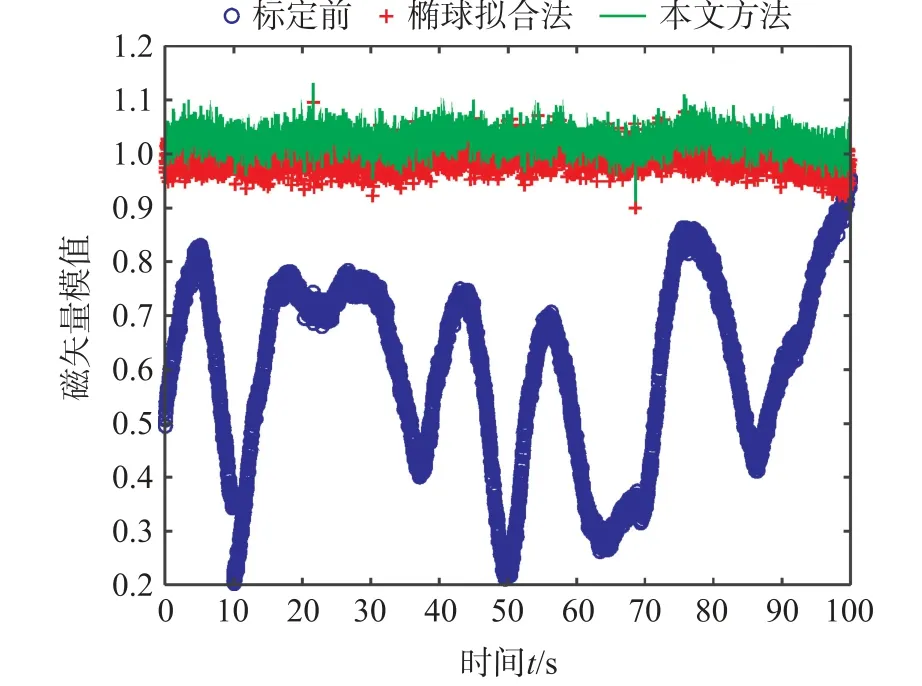
圖10 ICM20948 磁矢量模值標定前后對比圖

在圖11 中，可觀察到兩種標定方法標定后磁力計與慣性單元間的旋轉角。 其中，虛線表示橢球擬合法標定后矢量間旋轉角，實線表示本文方法標定后矢量間旋轉角。 從圖中可看出橢球擬合法標定后的矢量旋轉角波動較大，而經過本文方法標定后的矢量旋轉角波動較小。 在表1 中，可看到經過橢球擬合法標定后磁力計與慣性單元間旋轉角均值為29.69°，標準差為29.05。 經過本文方法標定后的磁力計與慣性單元間旋轉角均值為47°，標準差為1.682。 而蘇州地區的磁傾角為47.5°，考慮到消費級ICM20948 九軸MEMS 傳感器精度較低，可認為已完成磁力計與慣性單元間的未對準誤差標定。 因此，可認為本文提出方法在完成磁力計標定的同時，完成了加速度計與磁力計間的未對準誤差。

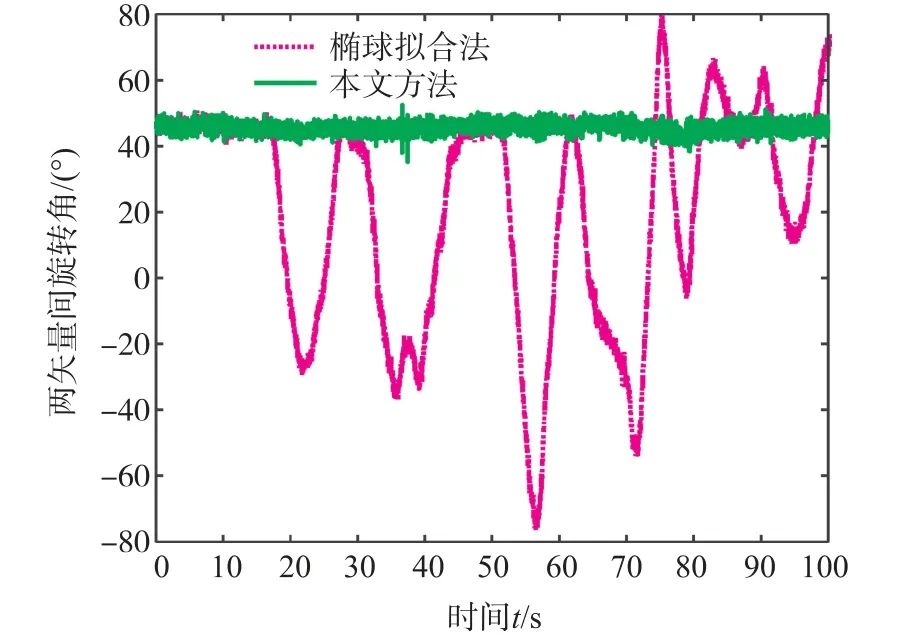
圖11 ICM20948 數據加速度計矢量與磁力計矢量間旋轉角

表1 標定后磁力計與慣性單元間旋轉角比較

4 結論

本文提出了一種基于遞推最小二乘法利用加速度計信息輔助標定磁力計的方法，在完成磁力計誤差參數估計的同時，也完成了加速度計和磁力計間未對準誤差的估計。 首先，對加速度計數據完成標定，再利用加計矢量與磁矢量間點積不變的性質，通過遞推最小二乘法對磁力計誤差參數進行估計，進而完成標定。 通過仿真與實際數據，對本文提出方法進行了驗證，結果表明，本文提出方法的標定精度與橢球擬合法相似，標定后的加速度計矢量與磁矢量間旋轉角約等于當地磁傾角。 相比橢球擬合法，本文提出的方法克服了由于無外部信息參考而無法確定磁力計誤差參數的影響。 并且通過遞推最小二乘法對磁力計誤差參數估計，計算效率高，可以快速完成標定。