壓電驅動器的電致振動特性研究?

方孟翔劉文光馮逸亭陳紅霞吳興意胡劍波

(南昌航空大學航空制造工程學院，江西 南昌 330063)

壓電驅動器因其輸出位移大、靈敏度高、抗電磁干擾和斷裂韌性強等優勢，廣泛應用于高應變材料精密定位、多層器件設計、便攜式電子器件的大規模制造工藝、微型機器人的超聲波電機和智能結構等領域[1－2]。 由于壓電驅動器的工作與其振動特性密切相關，所以深入了解電壓激勵下壓電結構的振動特性具有重要意義。

圍繞壓電驅動器的應用，研究者開展了大量的研究。 為抑制動態干擾對星光觀測系統成像質量的影響，姜世平通過構建比例積分微分反饋控制，建立了基于壓電驅動快反鏡的星光跟蹤控制系統[3]。以優化壓電結構驅動性能為目標，Henry 等研究了柔性變形機翼上分布壓電驅動器和機翼蒙皮間的最佳結構參數[4]。 采用最小二乘支持向量并設計內模控制器對壓電驅動器進行動態建模，尚愛鵬等實現了對壓電陶瓷驅動器的精密控制[5]。 應用旋轉軟體驅動器振動激勵下的運動機理，徐聰等人提出了一種基于壓電振動驅動的可旋轉軟體驅動器[6]。通過引入粒子群算法對模型參數進行優化，錢承等建立了壓電驅動器頻率相關的遲滯模型[7]。 利用低壓驅動下的大位移和快速響應能力，Chen 等設計了一種環形陣列式壓電驅動微透鏡驅動器[8]。 通過引入核函數和損失函數，紀華偉等建立了一種新的壓電陶瓷驅動器非線性模型，準確描述了壓電驅動器的遲滯特性[9]。 以提高壓電驅動器穩定性為目標，溫建明等提出了一種磁流變液慣性壓電旋轉驅動器，其各種性能均優于機械控制式壓電驅動器[10]。

無論何種形式壓電驅動器，其結構一直處于電壓激勵環境下。 圍繞壓電結構的電壓激勵振動，研究者做了大量工作。 基于能量原理，葉文強等分析了壓電懸臂梁的振動響應[11]。 結合Hamilton 原理和Rayleigh-Ritz 法，陳熹等建立了電壓激勵下四邊簡支壓電層合薄板的強迫振動方程[12]。 考慮摩擦因數的動態非線性和摩擦力分布的非線性變化，李爭等引入Hertz 接觸理論和Mindlin 理論建立了壓電驅動超聲電機的接觸模型[13]。 通過壓電陶瓷驅動器的輸出特性測試，榮雪媛等研究了輸入電壓與輸出位移的關系[14]。 結合伽遼金法和邊界值問題求解器，Chaterjee 等研究了靜電驅動壓電微懸臂梁的機電響應特性[15]。 使用Navier 法，Rouzegar 等求解了表面附有壓電纖維復合驅動器的層合板的運動方程，分析了不同幾何尺寸以及電載荷類型對結構動應力的影響[16]。 利用多場耦合條件下壓電殼的有限元力學模型，Liew 等討論了不同金屬和陶瓷體積分數對FGM 層合圓柱殼靜態響應和動態響應的影響[17]。 基于修正的三階剪切變形理論，Luo 等推導了壓電結構的運動控制方程，討論了壓電片的數量、厚度對驅動力和驅動力矩的影響[18]。

雖然國內外研究者在壓電驅動器的利用及其振動特性方面做了很多工作，但鮮有研究者對其進行橫向振動瞬態響應分析，且缺少理論與實際情況的結合。 由于壓電驅動器在一定條件下可轉化為梁模型，本工作基于能量法和熱力學平衡方程，推導了電壓激勵條件下壓電懸臂梁的強迫振動方程，測試了電壓激勵下壓電梁的諧響應和瞬態響應，分析了阻尼對壓電梁振動特性的影響，旨在為壓電驅動器的動力學設計提供參考。

1 壓電懸臂梁的運動控制方程

以圖1 所示雙晶壓電懸臂梁為對象。 假設壓電梁的基體長×寬×厚＝l×b×tm、壓電陶瓷的長×寬×厚＝l×b×tp。 壓電陶瓷鋪在基體的上下表面，沿厚度方向(z軸)極化并采用串聯方式連接。 假設沿z軸施加交流電壓，在逆壓電效應作用下，基體一側壓電陶瓷產生拉伸形變，另一側產生相反的壓縮形變，從而導致壓電懸臂梁產生橫向受迫振動。

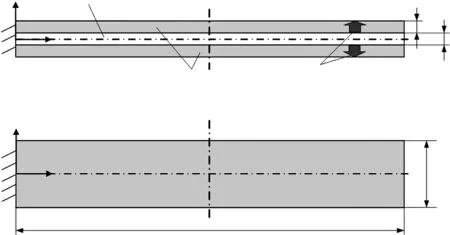
圖1 雙晶壓電懸臂梁幾何模型

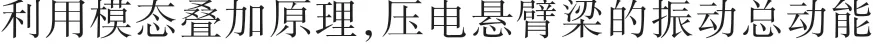
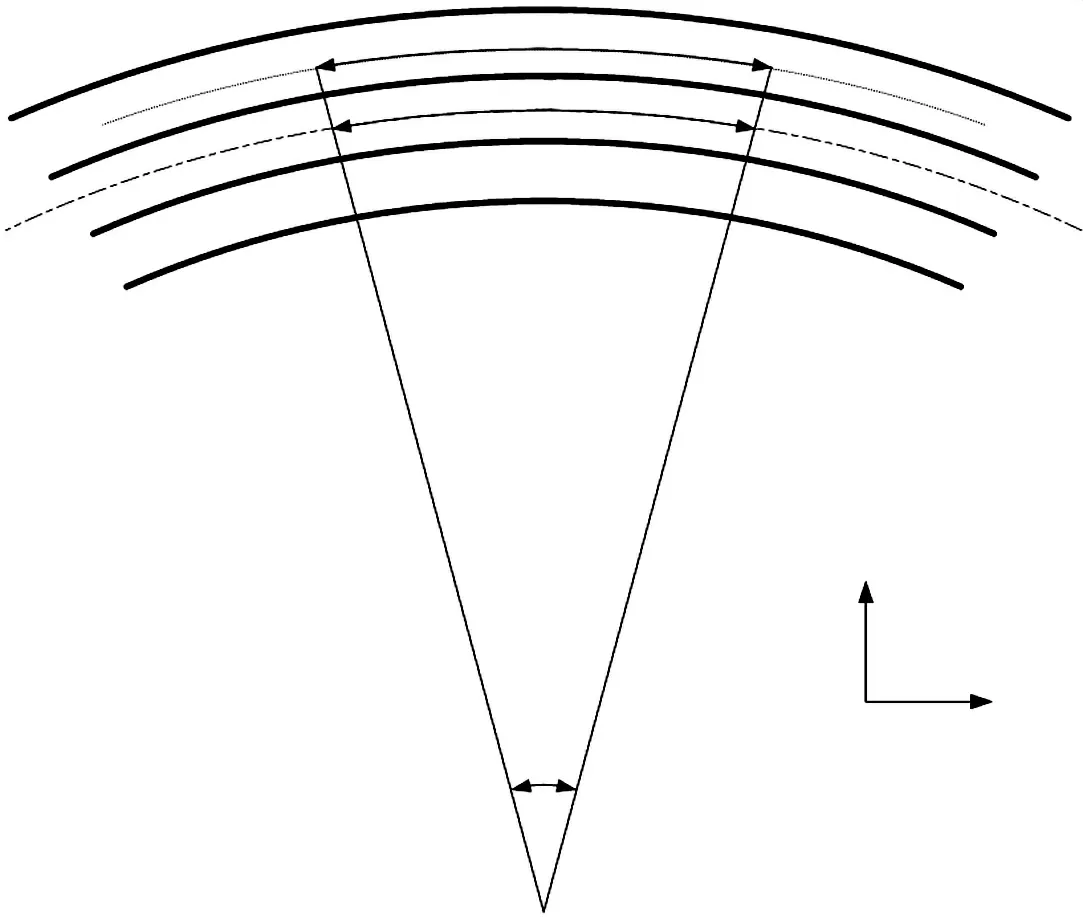
圖2 電壓激勵下壓電梁的彎曲變形

將方程(10)代入方程(7)、式(8)分別得到上、下層壓電陶瓷的應力表達式為:

電壓激勵下，非有勢力做的虛功δW為:

2 試驗研究

2.1 試驗件

如圖3 所示，試驗件是由市場購買的壓電片切制而成。 壓電陶瓷材料為PZT－5H，基體材料為黃銅。 壓電梁的幾何尺寸取l＝67 mm、b＝6 mm、tm＝0.2 mm 和tp＝0.19 mm。 材料參數由表1 給出。

圖3 雙晶壓電懸臂梁試件

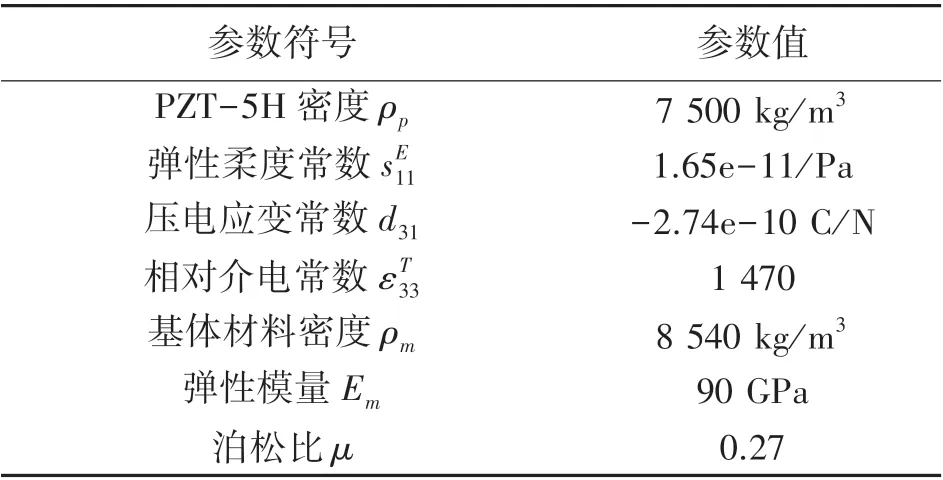
表1 PZT－5H 及基體材料參數

2.2 試驗方法

利用圖4 所示的試驗系統開展電壓激勵下壓電懸臂梁的振動測試。 試驗系統包括頻率特性分析儀FRA5022、多功能信號發生器WF1974、功率放大器HSA4052、激光位移傳感器HG－C1100、DHDAS 動態信號采集系統和計算機。

圖4 試驗系統

試驗開始前，給予已安裝固定好的試件初始瞬時激勵，然后記錄其自由振動瞬態響應曲線，多次測量取平均值，最后通過衰減系數法求出壓電懸臂梁的阻尼比ζ約為0.03。 使用頻率特性分析儀測得壓電懸臂梁的第一階固有頻率為55.513 Hz。 使用多功能信號發生器輸入電激勵信號，經功率放大器和導線在壓電懸臂梁的上下表面電極上施加電壓。 在壓電懸臂梁的共振頻率區間進行諧響應測試。 在壓電梁的共振、近共振和遠離共振頻率區間測試壓電梁的瞬態響應。 試驗過程中，利用激光位移傳感器測試壓電懸臂梁自由端的振動位移，并采集信號傳送到計算機進行顯示。

3 結果分析與討論

3.1 壓電懸臂梁的諧響應分析

如圖5 所示，試驗測量了不同幅值交流電壓激勵下壓電梁的諧響應。 結果表明，壓電梁的諧響應呈非線性特征，具有彈簧漸軟特性。 隨著激勵電壓增大，壓電梁產生的變形加大，梁的剛度隨變形增大而減小，導致壓電梁的共振頻率減小。 當壓電梁的激勵交流電壓分別為6 V、9 V 和12 V 時，結構的共振頻率分別為55.6 Hz、54.8 Hz 和54.4 Hz。 激勵電壓為9 V、激勵頻率為50 Hz 時，梁的振幅僅僅為0.117 mm。 將激勵電壓頻率增大至53 Hz 時，壓電梁的振幅將逐漸增大至0.216 mm；隨著激勵電壓頻率的繼續增大，此時壓電梁的振幅急劇增加，并且在54.8 Hz 時振幅達到最大值0.601 mm；當激勵電壓頻率大于共振頻率后，壓電梁的振幅急劇下降，在60 Hz 時減小至0.111 mm，相比其共振振幅下降了約81.5%。

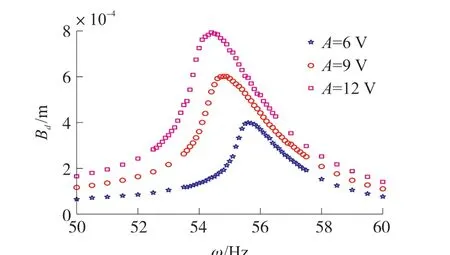
圖5 試驗測試幅頻特性曲線

圖6 為試驗結果與式(27)計算結果的比較。結果表明，不同激勵電壓下的試驗結果與理論計算結果較為吻合，驗證了本文推導電壓激勵強迫振動方程的可行性。

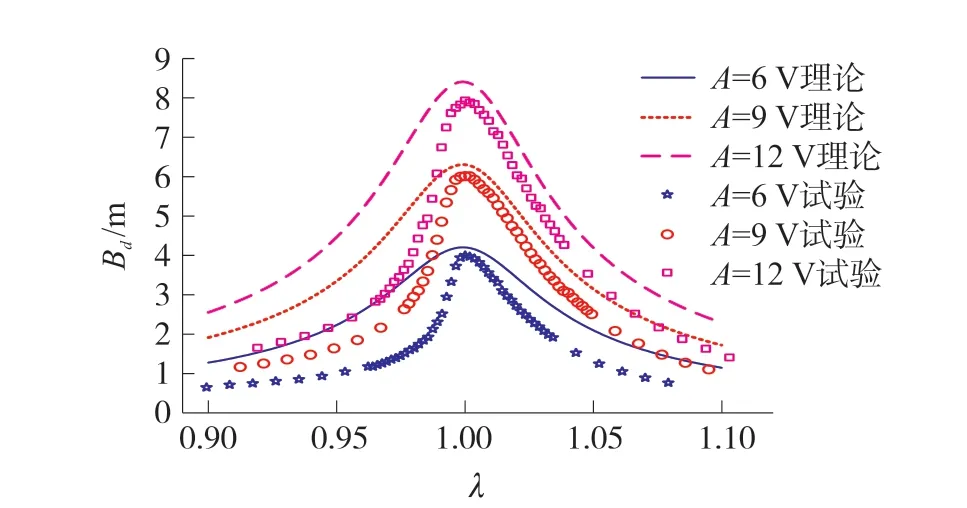
圖6 試驗與理論幅頻特性的比較

3.2 壓電懸臂梁的瞬態響應分析

圖7～圖9 分別研究了6 V、9 V 和12 V 電壓激勵下壓電梁的瞬態響應。 每種激勵電壓下，試驗分別測試了無量綱頻率λ＝1、λ＝0.87、λ＝0.53 時壓電梁的自由端位移在0.5s 內的時程響應曲線，并與式(26)計算得到瞬態響應結果進行比較。 圖10 計算了阻尼比ζ＝0.01 和ζ＝0.03 時的瞬態響應曲線，并與9 V 電壓激勵下壓電梁的試驗瞬態響應進行對比。 結果表明:

圖7 6 V 電壓激勵下的瞬態響應

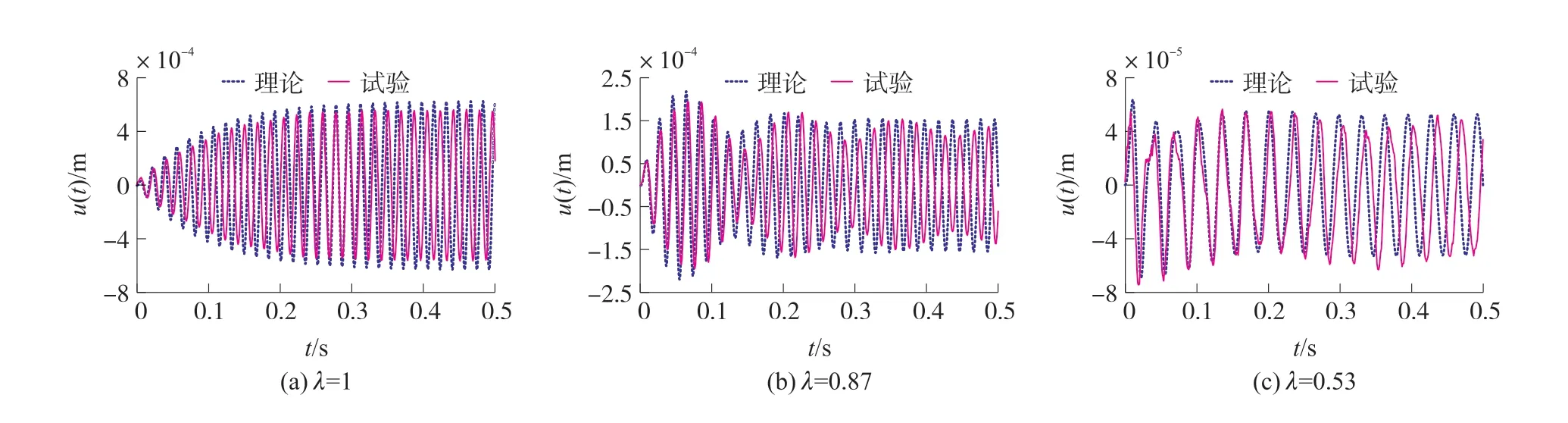
圖8 9 V 電壓激勵下的瞬態響應

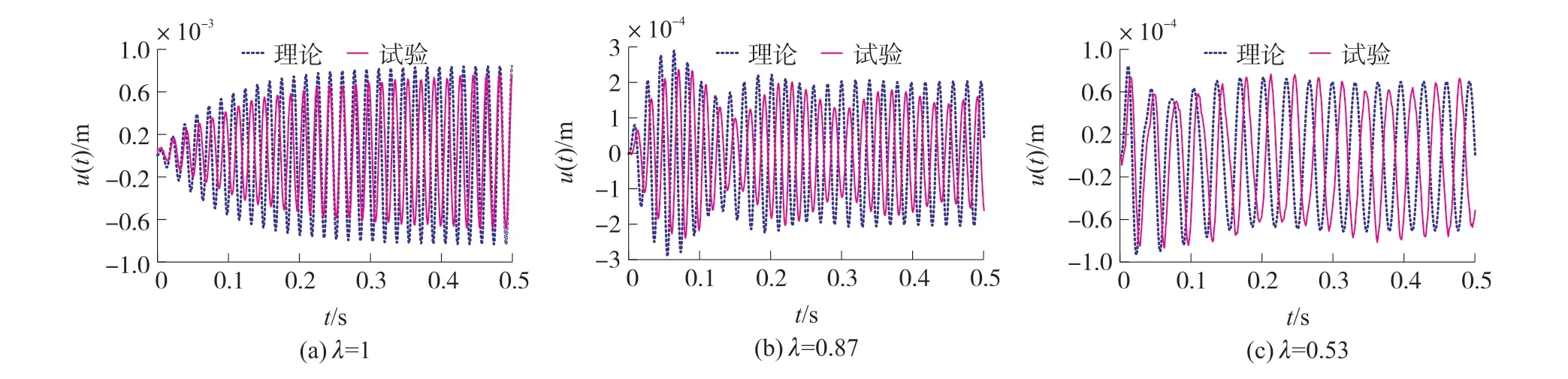
圖9 12 V 電壓激勵下的瞬態響應

圖10 不同阻尼比時的瞬態響應

①激勵電壓頻率等于共振頻率時壓電梁的振幅隨時間增加而增大，由于阻尼影響，壓電梁的振幅增大速率越來越小直至為零，系統達到穩態；激勵電壓頻率接近共振頻率時，瞬態響應曲線會出現“拍振”現象，但因阻尼消耗了能量，“拍振”振幅會隨時間逐漸減小直至消失，過渡到穩態振動階段；激勵電壓頻率遠離共振頻率時，壓電梁以激勵頻率做受迫振動，此時壓電梁的振幅與共振時相比十分微小。 當λ值相同時壓電梁的振幅隨著激勵電壓幅值的增大而增大。

②阻尼比越大，壓電梁的振動越趨于穩態狀態。λ＝1 且t＝0.5 s 時，ζ＝0.03 時壓電梁的振幅相比于ζ＝0.01 時下降了約62.0%；當λ＝0.87 時，ζ＝0.03和ζ＝0.01 第二個拍振振幅相比于第一個拍振振幅分別下降了23.4%和16.1%；λ＝0.53 時，阻尼大小對壓電梁振動抑制作用不明顯。

4 結論

基于能量法和熱力學平衡方程推導了電壓激勵下壓電雙晶懸臂梁的強迫振動微分方程，測試了電壓激勵下雙晶壓電懸臂梁的振動響應，理論與試驗結果相吻合。 試驗結果表明，壓電梁的振動響應呈彈簧漸軟特性，在6 V、9 V、12 V 交流電壓激勵下的共振頻率分別為55.6 Hz、54.8 Hz、54.4 Hz。 考慮工程實際中的非線性現象，若要增大壓電驅動器的驅動效率，增大激勵電壓幅值的同時還需適當減小激勵電壓頻率使其處于共振狀態。 阻尼對共振響應的抑振作用最明顯，9 V 共振頻率電壓激勵下，t＝5s時壓電梁在ζ＝0.03 時的振幅比在ζ＝0.01 時的振幅下降了約62.0%。 本文所得結論可為提高壓電驅動器的驅動效率問題提供理論與實踐指導。