基于多粒子群協同的城軌列車速度曲線多目標優化

徐 凱，楊飛鳳，涂永超，吳仕勛

(1. 重慶交通大學 信息科學與工程學院，重慶 400074；2. 重慶市公共交通運營大數據工程技術研究中心，重慶 400074)

列車自動駕駛ATO是城市軌道列車控制系統的重要組成。在列車運行過程中，ATO由已知信息進行優化調整，得到最優控制策略，給出控制力讓列車按照最優駕駛曲線運行[1]。目前對于ATO控制策略的優化，國內外主要采用的方法有粒子群算法PSO，遺傳算法GA和差分進化DE等智能算法[2-4]。

文獻[5]在求解列車自動駕駛速度曲線時， 采用改進后的粒子群算法，將多目標優化向單目標轉化，用加權求和的形式得到目標函數。上述傳統的加權方法忽略了各目標間的相互影響，沒有考慮他們之間的復雜關系，無法體現多目標優化的本質。為充分體現多目標研究的實質，通常采用Pareto原理來求解此類問題。而目前文獻基于Pareto原理優化時，往往只考慮兩目標問題，例如文獻[6]將時間和能耗作為兩個優化目標，混合了差分和模擬退火兩種進化算法進行求解；文獻[7]對比了兩種多目標優化算法MOPSO和NSGA_II，并驗證了在計算時間、可行解的多樣性以及Pareto前沿解的逼近程度等性能指標，MOPSO表現更佳，但卻未提及對MOPSO算法的深入改進。此外，為了保證行車安全和效率，城軌列車運行控制還有精準停車這一重要目標，即停車誤差不能超過30 cm。文獻[8]基于Pareto原理，采用MOPSO算法優化了能耗、時間以及停車誤差這三個目標，卻沒有評價算法的性能指標，特別是對算法收斂性能的改進。

此外，不同運行模式對列車能耗影響的研究相對較少[9]。文獻[10]在列車兩種不同的運行模式下，應用非現代智能算法，即時間逼近搜索這一傳統數學方法來求解問題。現有參考文獻在研究中，未同時結合列車多種運行工況序列和多目標優化，也未考慮各類工況序列對解集的影響以及各種模態下的性能指標評價等問題，這讓研究的復雜度及難度大大降低。

綜上，本文首先基于Pareto原理，以時間、能耗和停車精度為目標，再加以對列車運行中不同典型工況序列的分析，并結合列車運行多模態和多目標優化問題，提出一種協同進化的多目標混沌粒子群算法(Co-evolution Based Multi-objective Chaotic Particle Swarm Optimization，CMOCPSO)。經仿真試驗驗證，相較于MOPSO，本文算法在多樣性、收斂性指標方面得到了進一步改善。最后，為了獲取各類典型工況序列下最優的列車自動駕駛速度曲線，用模糊隸屬度法進行了篩選。

1 列車運行多目標優化模型

考慮到列車運行的復雜性，對其運動建模簡化為單質點，根據牛頓第二定律得到

ma=f(v,u)-g(v)-w(v,s)

(1)

式中：m為列車的質量；a為列車運行加速度；f(v,u)為列車運行時所受牽引力或制動力；g(v)、w(v,s)分別為列車運行時所受的基本阻力和附加阻力；v、u、s分別為列車運行速度、操控工況和線路位置。對于本文所提的牽引、制動、惰行及巡航4種列車運行工況，當f(v,u)大于0時，列車為牽引或巡航狀態；當f(v,u)等于0時，列車為惰行狀態，當f(v,u)小于0時，列車為制動狀態。

本文用時間作為迭代步長，列車運行位置及速度表達如下

(2)

si+1=si+Δs

(3)

式(2)、式(3)是計算列車行駛位置的迭代公式，si表示第i次迭代后的位置，ai由式(1)中a離散處理得到，s0=0，Δt=0.1 s。

Δv=vi+aiΔt

(4)

vi+1=vi+Δv

(5)

式(4)和式(5)表示在第i次迭代時列車速度vi的計算公式，v0=0，Δt=0.1 s。

在滿足安全等各種約束條件下，求解列車能耗、運行時間以及停車精度三個目標的計算模型如下。

站間運行時間為

T′=∑Δt

(6)

站間能耗指標[4]為

(7)

式中：E為能耗適應度；F為牽引力；v為列車運行速度；ξM為在牽引力作用下由電能轉為機械能的變換因子；A為輔助功率；T0為列車在站點間的實際運行時間；ξB為在制動力作用下，由機械能轉為電能的變換因子；B為制動力。

停車精度計算公式為

S′=∑Δs

(8)

D=|S′-S|

(9)

式中：D為停車精度；S′為列車在站間的實際運行距離；S為站間實際長度。

基于上述式(1)～式(5)建立的模型，列車運行多目標優化問題旨在求解得到一系列的工況轉換點{xi}，i=1, 2,…,m(xi∈ [ 0,S])，使得在式(11)的限制條件下，列車減少運行時間、降低能耗和提高停車精度。綜上，列車運行多目標優化問題表述為

min{T0,E,D}

(10)

約束條件為

(11)

式中：v0、ve分別為列車行駛初速度與末速度；vi為第i次迭代時列車實際的運行速度；vlim為對應的列車限速值；T′為列車實際運行時間；T0為計劃運行時間，s；S′為列車實際運行距離；S為站點間距，cm。

牽引(T)、制動(B)、惰行(C)和巡航(H)為列車運行中的四種工況，ATO將上述工況合理組合成多種工況序列。城軌交通不同于干線鐵路之處在于，站間距離相對較短，由于受限于線路長度，列車在站間行駛時工況轉換點不宜過多。原則上要求兩個工況轉換點距離不能過近，因為頻繁切換工況易造成不必要的損耗。此外，還應刪去列車在運行中有“制動”的操縱，例如“T-C-B-T-C-B”這種明顯費時又耗能的工況序列。

據此，去除那些違背工況轉換原則、既費時又耗能以及讓乘客不舒適的一系列操控序列，最終選出下述6種典型且可行的工況序列進行研究：①T-H-C-B；②T-C-H-C-B；③T-C-T-C-B；④T-H-T-C-B；⑤T-C-H-T-C-B；⑥T-C-T-C-T-C-B。

圖1是上述①～⑥6種工況序列下，采用本文所提出的算法求解得到的邊沿解和最優解空間的分布效果圖，圖1中的一個解即為一種列車自動駕駛方案。

由圖1可看出，6種工況序列對應的解的分布大不相同，此外不同工況序列的最優解也有所差異。這說明研究多種工況序列能夠改善算法解的質量，優化解的分布性和多樣性。

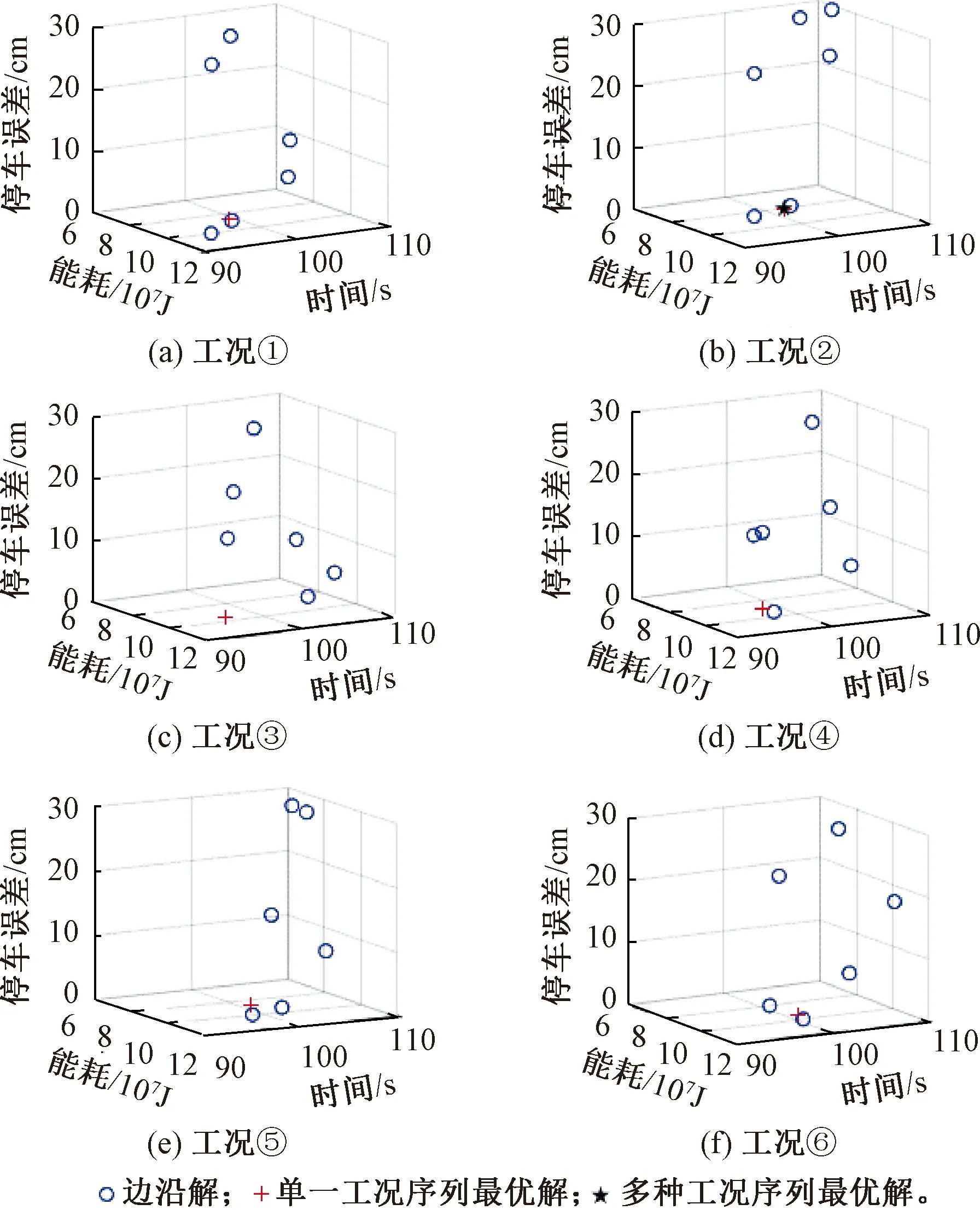
圖1 6種典型工況序列下邊沿解及最優解空間分布

2 基于協同進化的多目標混沌粒子群算法

2.1 CMOCPSO算法框架和思想

圖2是本文所提出的CMOCPSO算法框架，圖2中清晰地展示了所提算法的特點，采用全局和局部兩層結構實現并行搜索，各層內協同演化，引入雙外部檔案進行層間的信息交流，具體為：

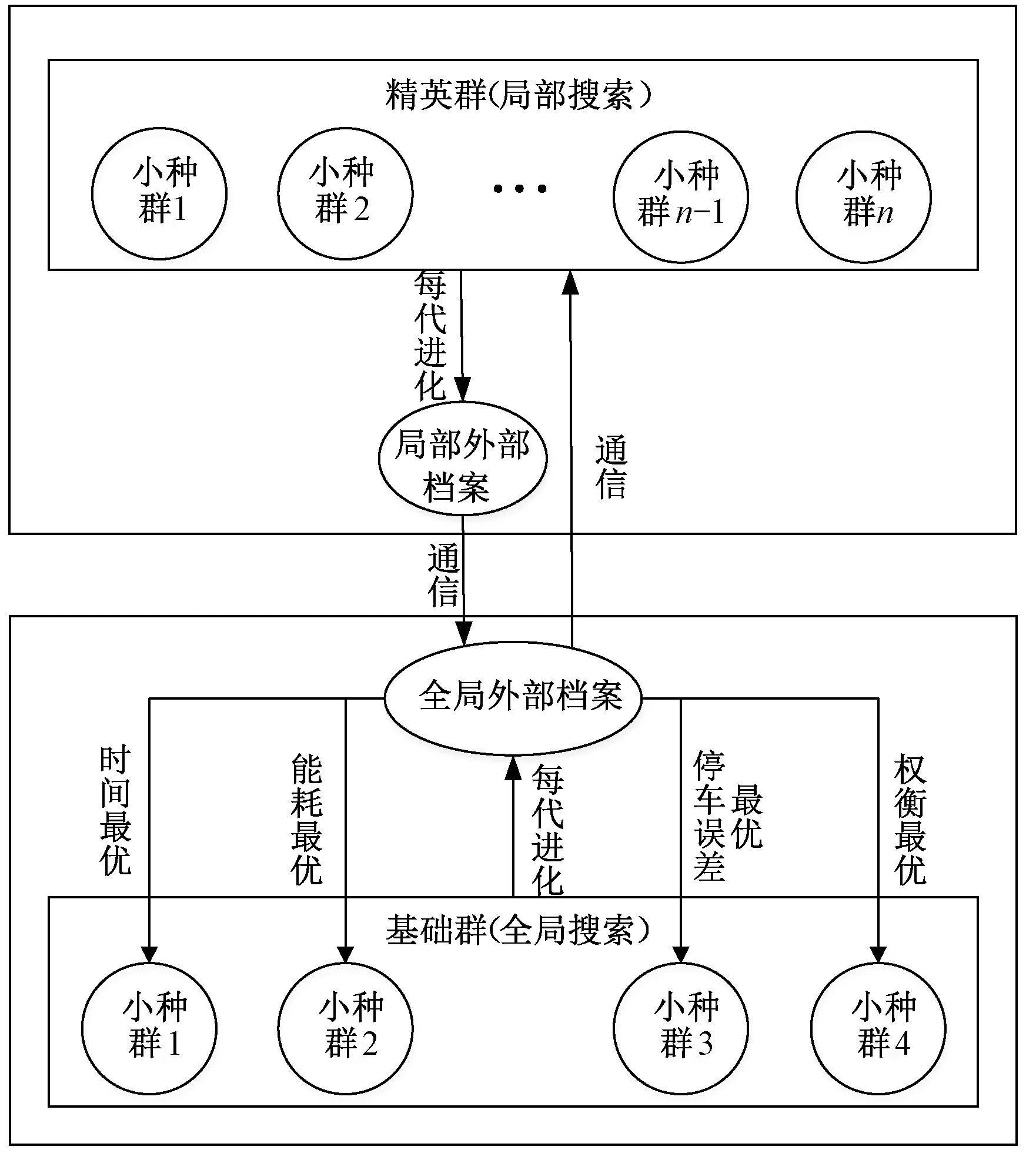
圖2 算法的總體框架

Step1分層設計。在圖2中分層結構用上下兩個虛線框標出。全局外部檔案與基礎群共同構成下層，其中基礎群的小種群有4個，協同演化，完成全局尋優；而局部外部檔案與精英群共同構成上層結構，其中精英群用于局部精細搜索，由n個小種群組成，協同演化深入挖掘出更多優質解。

Step2引入雙外部檔案，完善各層結構。在下層中，全局外部檔案接收基礎群中4個小種群每次迭代后的可行解，并通過Pareto支配獲取前沿解。再從前沿解的解集里選取時間、能耗、停車誤差及權衡最優的4個粒子，并分別返送回與之對應的基礎群小種群中；與下層有所不同，上層精英群中n個小種群每進化一次，局部外部檔案就接收其產生的可行解，由支配關系判斷后得到Pareto前沿解即可。

Step3上下層之間以T為周期實現信息交互，加速搜索過程。每間隔T次迭代，在下層的全局外部檔案解集中選出n個精英解，經過擾動處理產生與之對應的n個新精英小種群，共同實現局部搜索，使得精英解周圍潛在的優質解得以充分挖掘；并且，在本次交互周期里，下層全局外部檔案將接收上層局部外部檔案獲得的Pareto前沿解。

2.2 混沌粒子群算法

粒子群優化PSO算法為一種并行隨機的啟發式搜索方法，其粒子的移動速度和位置的計算模型為

(12)

(13)

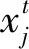
混沌具有良好的遍歷性，可以幫助算法快速跳出局部最優。結合搜索速度快且能力強的PSO，便能相互取長補短，即形成全新的混沌粒子群算法CPSO。此處選用典型混沌系統Logistic方程

L_r1(j+1)=μL_r1(j)[1-L_r1(j)]

(14)

L_r2(j+1)=μL_r2(j)[1-L_r2(j)]

(15)

式中：j為粒子序數；μ為控制參數，0≤μ≤4；當μ=4且0≤L_rk(1) ≤1(k=1,2)時，系統為完全混沌狀態。用L_r1(j)和L_r2(j)替換式(12)中的r1和r2，發揮混沌在算法中的遍歷性，既可以避免粒子陷入局部最優，又能使算法快速搜索到全局最優解。

2.3 基礎群的進化策略

在進行全局搜索時，多目標優化有別于單目標優化，它引入一個全局外部檔案。所以，式(12)和式(13)不再適用于本文所提算法，需對其進行修正，從而得到新的粒子速度及位置更新公式為

(16)

(17)

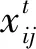
策略1(常規法)：把基礎群均勻分成4個小種群，從全局外部檔案中隨機選取4個Pareto前沿解作為4個小種群對應的gBest′。

策略2(目標引導法)：基于待優化的3個目標，可以把基礎群劃分為4個小種群，其中前3個小種群的進化具有指向性，其各自對應的gBest′從全局外部檔案中時間、能耗及停車精度極端最優粒子中選出，分別用以優化時間、能耗及停車精度這3個指標。這種方式使得各個目標的邊沿最優解得到最大限度挖掘。而第4個小種群則用于3個目標的綜合權衡尋優，從全局外部檔案Pareto前沿解集中隨機選取一個作為其對應的gBest′，稱為權衡最優粒子。

策略2采用一個小種群與一個目標優化相對應的方法，使得各目標上的邊緣最優信息得到更大程度地挖掘，而所有目標的綜合優化由剩余的第4個小種群負責，讓可行解的分布更加均勻。在此策略下，基礎群形成了一個全方位、高效協同的搜索粒子群體。本文后續試驗中驗證了該策略的優越性。

2.4 精英群的進化策略及其實現

上下兩層之間進行通信，一旦通信周期到來，從下層全局外部檔案的Pareto前沿解集中獲取n個精英解，將它們送入上層的精英群，并對其進行擾動，產生n個相對應的精英小種群。其中每一個小種群有m個粒子，用來搜尋這n個精英解周圍更多潛在的優勢解。精英小種群生成公式為

Xi1=l_besti

(18)

Xij=l_besti+λrand()

(19)

式中：Xij為精英群的第i個小種群中的第j個粒子；l_besti為第i個小種群擾動所用粒子；λ為精英群約束步長的最大值；rand()為-1到1之間的隨機數。

需要說明的是，為了實現更為精細的搜索，精英群的搜索步長一般要小于基礎群，將其限制在一個較小的范圍內。

2.5 算法流程圖

基于策略2的CMOCPSO算法的流程見圖3。

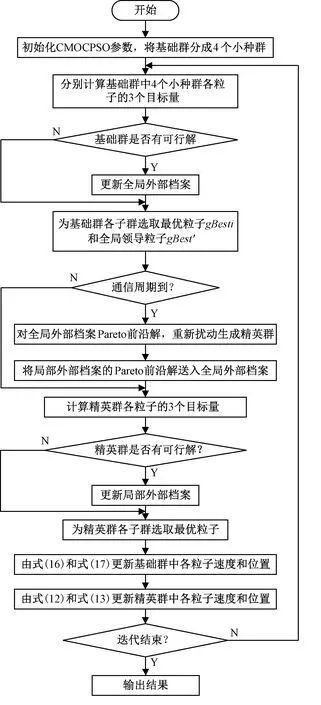
圖3 基于策略2的CMOCPSO算法流程

3 仿真試驗及分析

3.1 仿真參數設置

(1)線路及列車相關參數。本文仿真試驗選用重慶輕軌六號線某一區間段。在該區段上，站間限制速度為80 km/h，站內限制速度為60 km/h，線路區間長1 620 m；列車在行駛中影響基本阻力的因素較多且復雜，在實際應用中用理論公式難以表述，可由大量試驗綜合得到的經驗公式來計算[11]，這里的基本阻力公式及列車參數的選用參考了文獻[12]。列車全長120 m，4節動車車廂，2節拖車車廂，動車質量35 t/節，拖車質量34 t/節；列車區段的目標運行時間為90～110 s。

(2)算法參數設置：CMOCPSO算法中基礎群有4個小種群，每個小種群有50個粒子。精英群中小種群個數為4，每個小種群粒子數為10，共40個粒子，學習因子c1、c2和c3取值均為2，慣性權重因子w取值為1，最大進化代數為100；MOPSO粒子總數為100，最大進化代數為200。這兩種算法函數評價次數均為20 000次。

(3)通信周期T設置：在上述圖2中，通信周期是指上下兩層進行雙向信息交互時所需經歷的進化代數T。參數T的設置在很大程度上影響Pareto前沿解集的分布，若該值過大，就意味著通信次數過少，容易使精英群長期滯留于某些局部搜索區域，很難跨區域實現更精細的尋優，最終會導致整個解集的分布不均勻；若該值過小，表示兩層間交互過于頻繁，這將導致精英群搜索效率低，不能深入挖掘可行解。

圖4采用T-H-C-B工況序列。基于本文算法，在三種交互周期T=5、10和20下可得對應解空間分布的對比圖。對于不同通信周期T下的解空間，圖4中以3種符號分別表示。由圖4可知，相較于T=5或T=20，當T=10時，在能耗和時間指標上有明顯優勢，這也證明了試驗結果與前述分析吻合，因此在后續試驗中通信周期T取10。

圖4 不同通信周期下的解空間分布圖

3.2 算法性能評價指標

為了驗證本文算法的優越性，還須先明確下列幾個指標，用以度量算法的收斂性和多樣性。

(1)收斂性指標GD及γ

(20)

式中：n為算法所獲Pareto前沿解的個數；di為第i個解與真實Pareto前端的最小距離。

(21)

式中：G={g1，g2，…，g|G|}為算法獲得的Pareto前沿解集；r*={r1，r2，…，r|r*|}是真實的Pareto前沿解集。

上述指標GD及γ的值越小，則算法有更好的收斂性。

(2)多樣性指標SP、Δ分別為

(22)

(23)

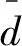
上述指標SP及Δ的值越小，表示解集分布越均勻。

3.3 試驗結果及分析

本文將兩種不同策略和兩種不同算法分別獨立運行，其次數均為20，并從以上收斂性、多樣性指標和Pareto前沿解個數等多個角度出發，對試驗結果進行統計分析，對比兩種不同策略及算法的優劣。

3.3.1 CMOCPSO算法策略的選取

對比2.3節中提到的兩種策略，即常規法和目標引導法，其相關指標統計結果如表1所示。

表1 兩種不同策略下的算法性能評價指標對比

由表1可知，在算法的收斂性、多樣性以及Pareto前沿解的個數等方面，目標引導法都優于常規法。因此，在后續試驗中，CMOCPSO算法采用策略2，用目標引導法選取全局領導粒子，并將其與MOPSO算法從多方面比較分析。

3.3.2 兩種算法下的收斂性和多樣性分析對比

采用多目標粒子群MOPSO和本文所提出的CMOPSO算法進行仿真試驗對比，其統計結果如表2所示。

表2 兩種不同算法的性能評價指標統計

表2比較了Pareto前沿解的收斂性、多樣性以及數量這三個方面的指標。從表2中可知，除了多樣性SP的均方差這一項指標上CMOCPSO與MOPSO兩者持平，在剩余的各個指標上，CMOCPSO算法都具有明顯的優勢。進一步分析各項指標平均值，可知CMOCPSO不僅能加快算法收斂速度，而且還能提高可行解的多樣性，較大程度增加了解的個數。

上述兩種算法在Pareto解空間與前沿解的分布情況見圖5和圖6。

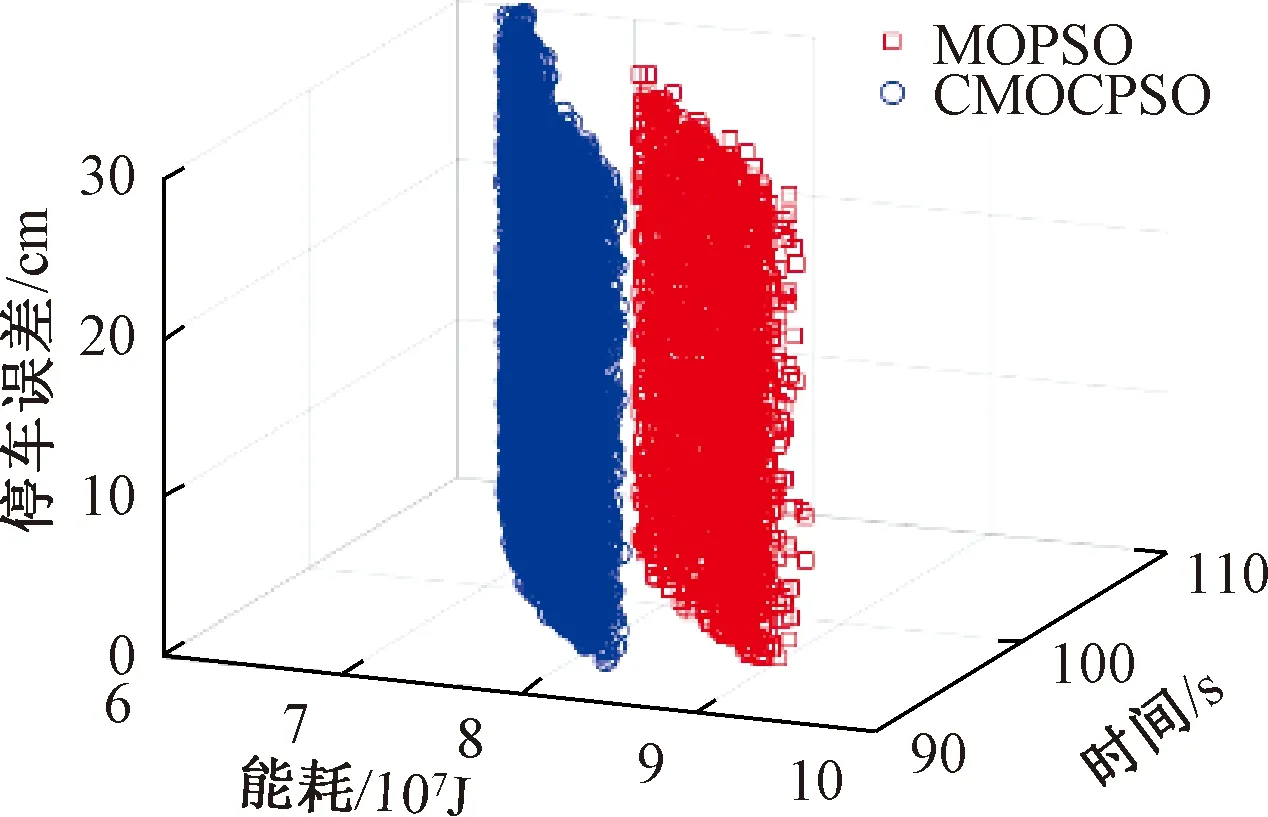
圖5 不同算法下的Pareto解空間比較

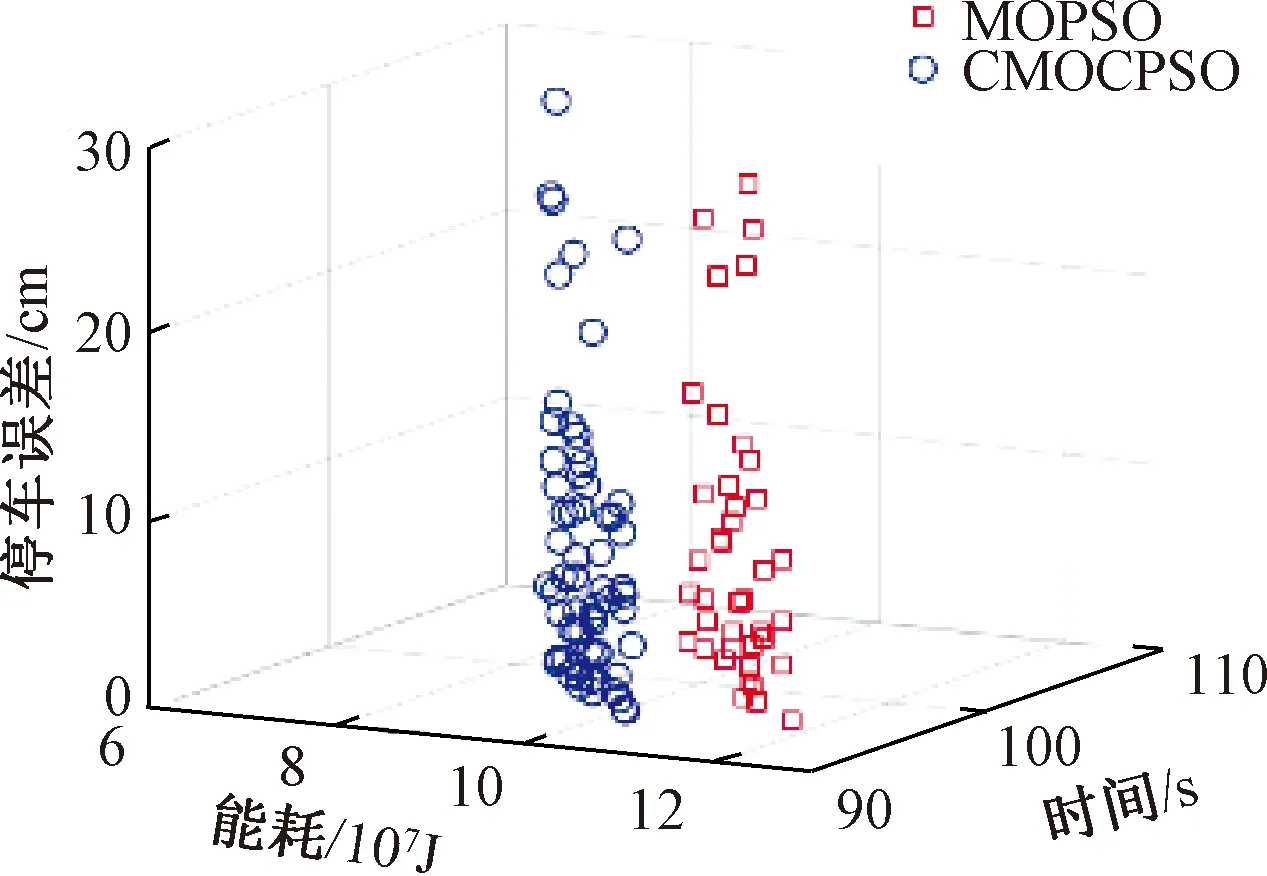
圖6 不同算法下的Pareto前沿解比較

由圖5和圖6可知，相較于MOPSO，CMOCPSO算法具有更好的收斂性。從總體上看，由它計算所得到的能耗明顯更小，時間更短；同時，CMOCPSO在可行解上呈現出更好的分布性，各目標對應的解空間跨域范圍更廣，且Pareto前沿解的數量更多。

3.3.3 兩種算法的時間復雜度分析

對于MOPSO算法，設I1為算法迭代最大次數，h為目標個數，m為種群粒子總數。只要算法迭代次數與粒子數足夠大，可以忽略對低次冪的計算[13]。因此，MOPSO算法的時間復雜度關鍵取決于外部檔案的更新，其計算過程為：1×h×m2+2×h×m2+…+(I1-1)×h×m2=0.5×h×(I1-1)×I1×m2≈6×108。

對于CMOCPSO算法，設I2為算法進化最大次數，h為目標個數，上下層之間的交互周期T=10；其中下層基礎群有4個小種群，每個小種群有k個粒子，上層精英群有n個小種群，這里的n=4，每個精英小種群有k1個粒子；全局和局部外部檔案的規模，即至多可容納的Pareto前沿解數目分別為A1=1 000，A2=100。

在CMOCPSO算法中，全局與局部外部檔案的更新，以及將局部外部檔案的解向全局外部檔案更新，以上三個過程占據了主要的時間計算復雜度。

其中，對全局外部檔案進行更新的時間復雜度計算為：1×h×42×k2+2×h×42×k2+…+(I2-1)×h×42×k2=0.5×h×(I2-1)×I2×42×k2≈6×108。

最后，局部外部檔案的解向全局外部檔案更新的時間復雜度計算為A1×A2×(I2/T)=1.0×106。

綜合分析可得該算法時間復雜度是6.25×108。

綜上所述，以上兩種算法的時間復雜度均處于一個數量級，是一種較為理想的狀態。為了獲取更好的算法性能指標，僅犧牲少許的時間復雜度是合適的，這符合算法改進的基本準則[14]。

3.4 各類工況序列最優方案的選定

基于Pareto原理的多目標優化結果是一個解集。在列車運行優化問題中，一種列車自動駕駛方案對應于一個Pareto解。本文采用模糊隸屬度函數對解中每個目標對應的隸屬度進行評價，以此篩選出不同工況序列下最優的駕駛方案。所述模糊隸屬度函數的定義為[15]

(24)

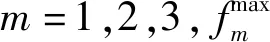
利用式(25)，可以求得每個解的滿意度值，則最優的駕駛方案即為最大滿意度值所對應的Pareto解。

(25)

式中：Ψi為第i個Pareto解對應的滿意度值；A為外部檔案的規模。

針對本文所述的6種典型工況序列，采用上述模糊隸屬度法對各自工況的Pareto前沿解集進行了篩選，得到對應的最優駕駛方案，見表3。

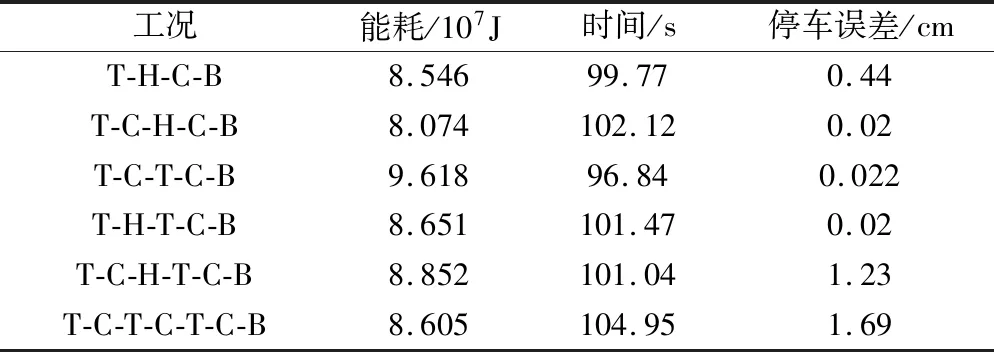
表3 各典型工況序列下的最優方案

圖7是表3中各類典型工況序列下的速度-距離曲線，分別用6種不同的顏色曲線標明。

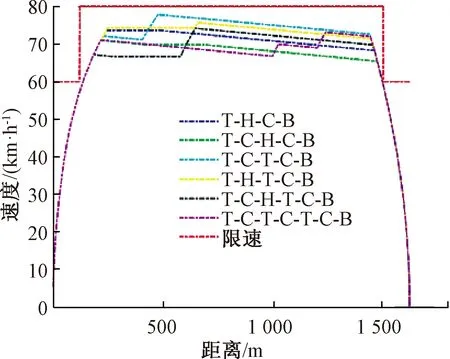
圖7 各典型工況序列下的最優速度-距離曲線

在利用CMOCPSO獲得Pareto前沿解集后，可以從這些解集中選出能耗最低、用時最少以及停車精度最高的各類不同工況序列與其對應的控制策略。由表4可知：工況序列為T-H-C-B時，能耗最低；工況序列為T-H-C-B時，用時最少；工況序列為T-H-T-C-B時，停車精度最高。

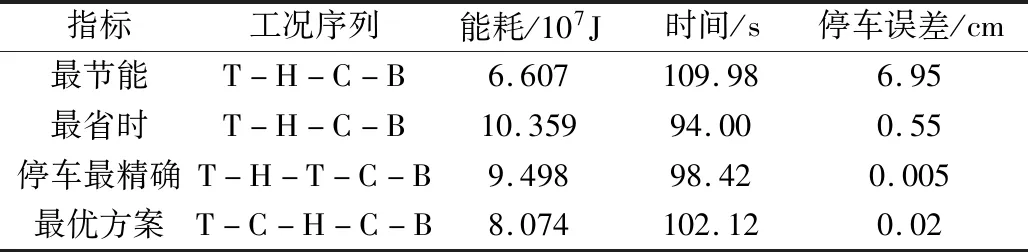
表4 多種工況序列對應的極端解和最優策略

根據式(24)和式(25)，再結合表4進一步得到：工況序列T-C-H-C-B是多種工況序列下的最優策略，圖8是該工況序列下的最優速度-距離曲線。此外，由表4中的統計數據可以看出，從多種工況序列解集中應用模糊隸屬度方法篩選出的最優策略，在每個目標上的值都相對均衡；再由表3分析可得，相較于其余5種運行工況模式，本文確定的各類工況序列下的最優方案T-C-H-C-B最少在對應的兩個目標上呈現出的效果更佳。

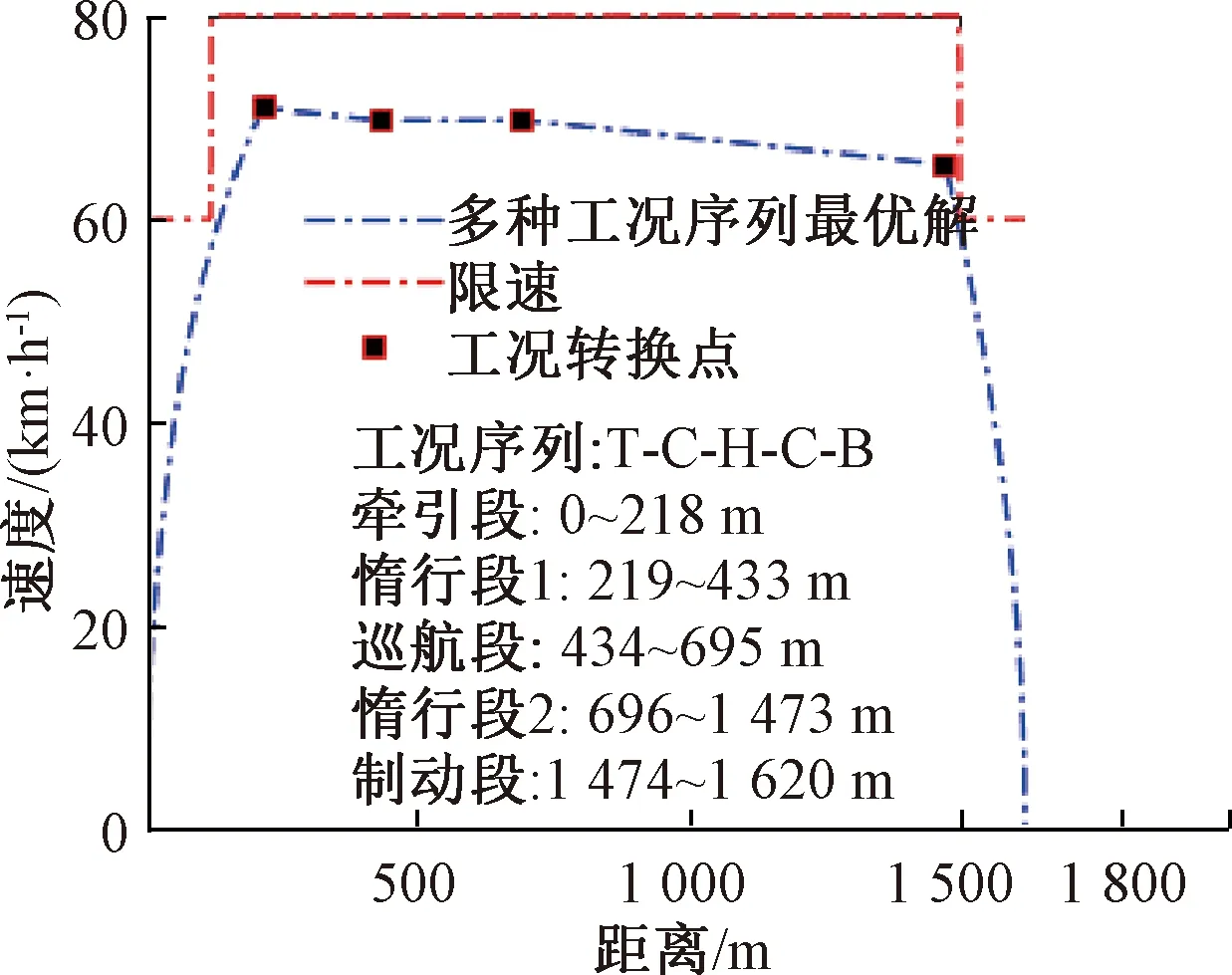
圖8 多種工況序列對應的最優速度-距離曲線

綜合表3和表4的各項數據可知，僅研究單一工況序列將存在解的多樣性低、空間分布不均勻且數量少的問題。因此，對多種工況序列進行分析與挖掘，這對實際工程的應用是具有研究價值的。

4 結論

針對城軌列車運行速度曲線優化問題，本文提出了一種新穎的協同進化多目標混沌粒子群CMOCPSO算法進行求解，通過仿真試驗驗證及分析，得到下列結論：

(1)在多種工況模式下，對應解的分布存在較大的差異。相較于單一的工況序列，在解的數量和質量上，多種工況序列下的解都具有明顯的優勢，因此可獲得數量多且優質的列車自動駕駛策略。

(2)與MOPSO相比較，采用目標引導策略的CMOCPSO算法，通過設置恰當的通信周期，其可行解在多樣性、收斂性和數量等多個指標上性能更優，從而最終獲得的列車運行速度曲線也最佳。

(3)相較于其余5種工況模式所對應的最優駕駛策略，這里采用模糊隸屬度法，從不同典型工況序列的Pareto解集中選擇出最優駕駛方案，使得列車運行能耗、時間和停車精度這3個目標至少有2個表現良好。