基于Bagging-CVA的動態過程及質量相關故障檢測
郭小萍, 郭建斌, 高嘉俊, 李 元
(沈陽化工大學 信息工程學院,遼寧 沈陽 110142)
工業過程故障檢測是保證產品質量和運行安全的關鍵。目前基于數據驅動的故障檢測技術得到飛速發展[1-2],國內外已有許多研究成果,如基于主元分析(Principal Component Analysis,PCA)[3-4]、偏最小二乘(Partial Least Squares,PLS)[1,5]和典型變量分析(Canonical Variate Analysis,CVA)[6-7]等的故障檢測方法。傳統故障檢測方法通常在檢測出系統故障時發出報警,不顯示該故障是否對質量產生影響的信息。隨著現代生產過程對產品質量的要求不斷提高,技術工程師和企業管理者更關心故障發生時,是否會影響到產品質量。目前對質量相關故障的檢測方法的研究開始受到越來越多的關注[8-9]。過程發生故障時,根據故障是否影響最終產品質量,可以將故障進一步劃分為質量相關故障和非質量相關故障[10]。
傳統CVA方法可以提取過程變量與質量變量之間最大相關性,建立質量相關故障檢測系統,監測質量相關故障對質量的影響。由于非質量相關故障對質量無影響,當生產過程發生此類故障時,質量相關故障檢測系統不報警,從而發生漏報。Zhu等[11]通過PCA和CVA相結合的方法,能夠對過程相關故障和質量相關故障同時進行監控。在生產過程中采集的數據通常具有時序相關性,該性質可能會對故障檢測模型的精準度產生影響[12-13]。為了提高模型的性能,動態CVA(Dynamic CVA,DCVA)方法[14-15]采用Hankel增廣矩陣構造動態相關矩陣進行建模,降低了數據時序相關性對模型的影響。但新構造的增廣矩陣由于維度的擴展,增加了檢測所需時間。基于滑動窗CVA(Moving Windows CVA,MWCVA)方法[16]通過滑動窗口構建動態相關矩陣。但如何選擇最優窗寬參數是一個難題,窗寬太小會遺漏某些過程數據信息,降低檢測性能,窗寬太大又會增加檢測所需時間。Ge等[17]提出基于Bagging的SVDD(Support Vector Data Description)故障檢測方法,首先使用Bagging隨機抽樣形成多組訓練集,消除時序相關性,然后使用SVDD方法建立多個模型,采用貝葉斯方法對多個統計量進行融合。但該方法在故障檢測時,需要計算多組模型的統計量并進行融合。
本文提出一種基于Bagging思想和典型變量分析(Bagging-Canonical Variate Analysis,Bagging-CVA)的動態過程及質量相關故障檢測方法。針對時序相關性的問題,采用Bagging思想對建模數據進行隨機抽樣構成多組新的訓練集,消除建模數據間的時序相關性;對每組新的訓練集采用CVA方法分別建立過程故障檢測模型和質量相關故障檢測模型。基于多個模型對不同故障的檢測率和誤報率,提出了一種最優模型選取策略,對選出的檢測率最高模型和誤報率最低模型所對應的統計量進行融合,并作為最終故障檢測統計量,減少故障檢測采用多組模型結果進行融合的復雜度。在過程故障發生時,所提出的方法可以同時觀察該故障是否影響產品質量。最后通過數值案例和TE過程仿真實驗驗證了所提方法的有效性,并與PCA、CVA和傳統Bagging-CVA等方法進行了對比。
1 CVA原理
CVA的原理是在矩陣X=[x1,x2,…,xm]T∈Rm×p和Y=[y1,y2,…,ym]T∈Rm×q之間尋找最優投影方向a和b,使得投影后的典型變量l和w具有最大的相關性。其中m為樣本數,p和q分別為矩陣X和Y的變量數。CVA的目標函數為
(1)
式中,ΣXX,ΣYY分別為X和Y的自協方差矩陣;ΣXY為X和Y之間的互協方差矩陣。上述優化問題可通過奇異值分解方法[7,14]實現:
(2)
式中,U和V分別為矩陣H的左右奇異矩陣;對角陣為D=diag{ρ1,ρ2,…,ρd},其對角線元素為典型變量間的相關系數,且ρ1≥…≥ρd,d=min{p,q}。投影矩陣A和B可以通過式(3)計算得出:
(3)
2 改進Bagging-CVA故障檢測
2.1 CVA故障檢測模型建立
采用CVA方法建立過程故障檢測模型和質量相關故障檢測模型。
(1) 過程故障檢測模型。
使用過程數據集X,構造H矩陣并利用廣義奇異值對其進行分解,計算公式為
(4)
根據式(3)計算得到最優投影矩陣Akx,其中Akx為矩陣A的前kx列,可以由典型變量間的相關系數累計貢獻率[1,18]確定。確定過程相關的典型變量估計矩陣為
C=XAkx∈Rm×kx
(5)
(6)
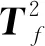
(2) 質量相關故障檢測模型。
利用過程數據集X和質量數據集Y并根據式(3)進行CVA分析得到最優投影矩陣Aky。利用過程相關數據X構造質量相關的典型變量估計矩陣E和殘差矩陣G:
E=XAky∈Rm×ky
(7)
(8)
矩陣E和G描述了過程變量和質量變量之間的信息,可以通過過程數據檢測質量相關故障,構造相應的統計量[14]:
(9)
2.2 最優故障檢測模型確定
過程數據通常具有很強的時序相關性,此類特性會對故障檢測模型的精準度產生一定的影響。傳統CVA方法通過采用增廣矩陣的方式對過程數據進行預處理,可以降低過程數據時序相關性對故障檢測模型性能的影響。然而,使用矩陣增廣的數據處理方式,會產生一定的檢測延遲。此外,使用增廣后的數據矩陣進行典型變量分析可能會導致非正定矩陣的產生,對所建故障檢測模型的性能產生巨大影響。針對上述問題,使用Bagging思想對過程數據進行預處理,消除過程數據的時序相關性。
Bagging算法[20-21]是一種集成算法,其基本原理是對原始數據集進行可重復抽樣。每次從數據集中隨機有放回地抽取一定數目的樣本,這些樣本組成一個新的訓練集(稱為一個袋),重復M次后,形成M組新的訓練集。然后,使用M組新的訓練集進行訓練,并將最后的結果進行融合。在Bagging方法的基礎上,提出一種最優模型選取方法,具體選取流程如圖1所示。
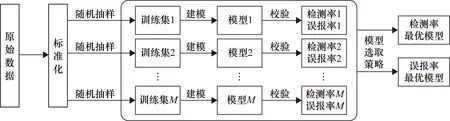
圖1 基于Bagging算法思想的故障檢測模型建立流程圖
(1) 通過Bagging算法獲得M組新的訓練集,分別利用CVA方法建立M個過程相關故障檢測模型和M個質量相關檢測模型。
(2) 使用校驗數據對這些模型進行校驗,獲得相應檢測率和誤報率。
(3) 通過設計一種模型選取策略確定最優模型,即設檢驗數據中有I類故障數據,應用所建立的M個檢測模型中的每個模型會得到I個檢測率和I個誤報率,則可以構建一個檢測率矩陣:
(10)
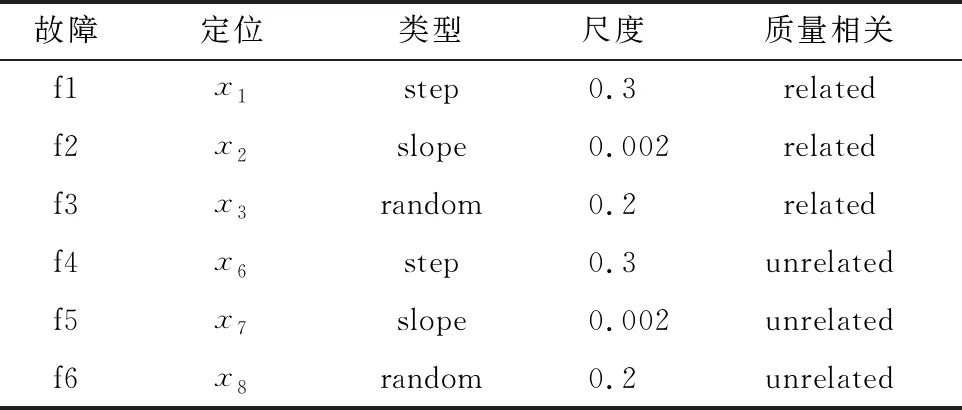
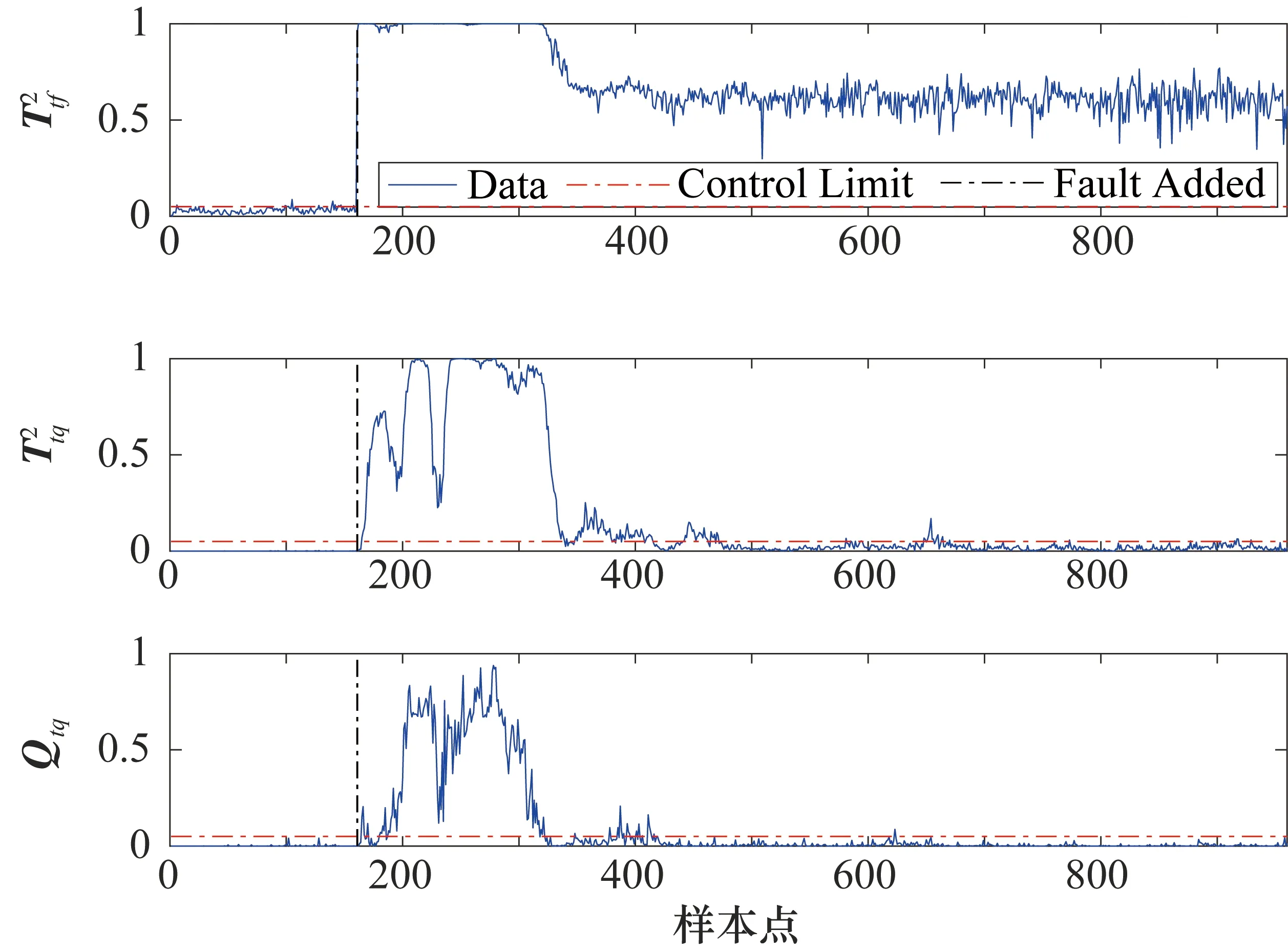
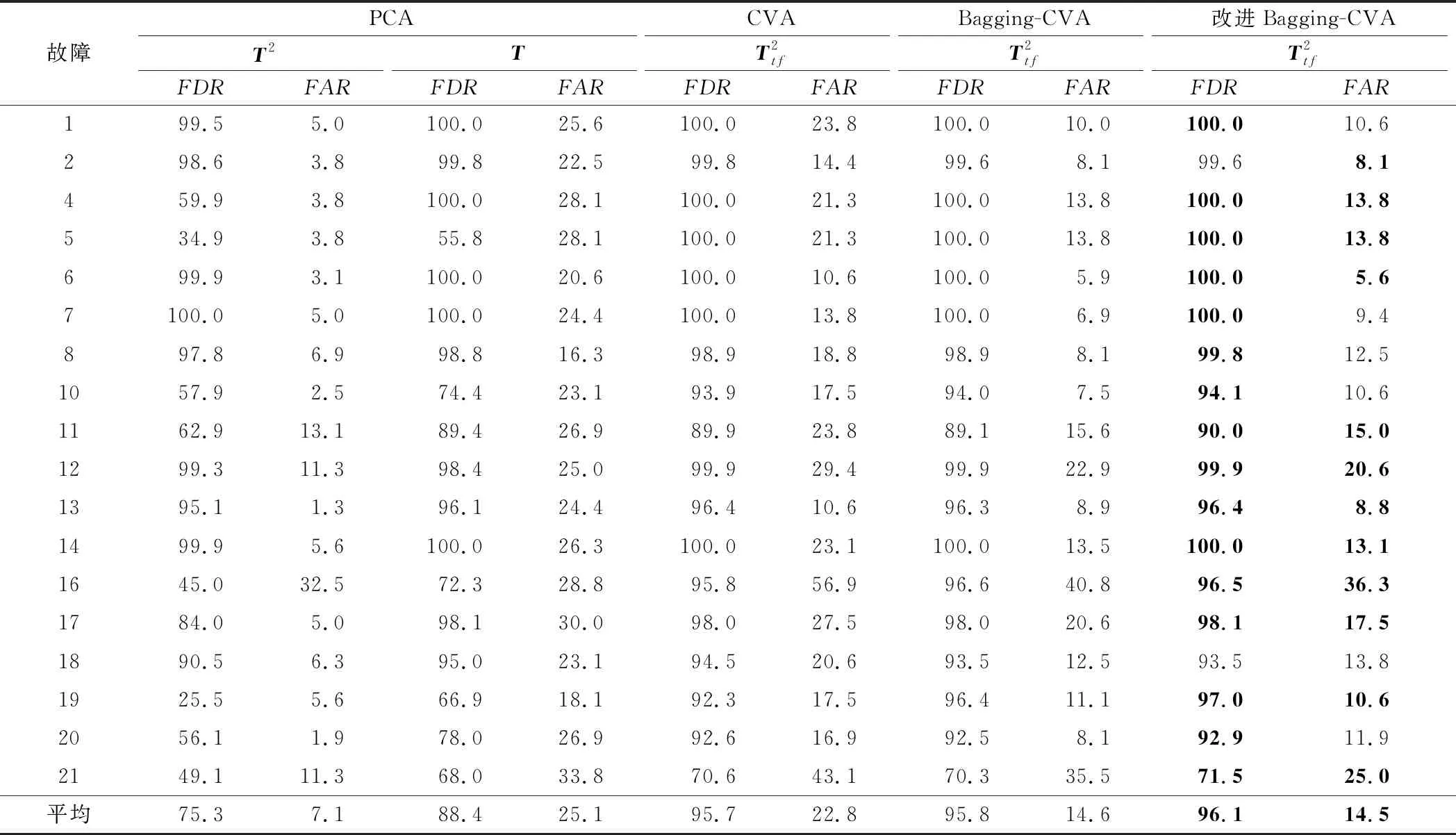
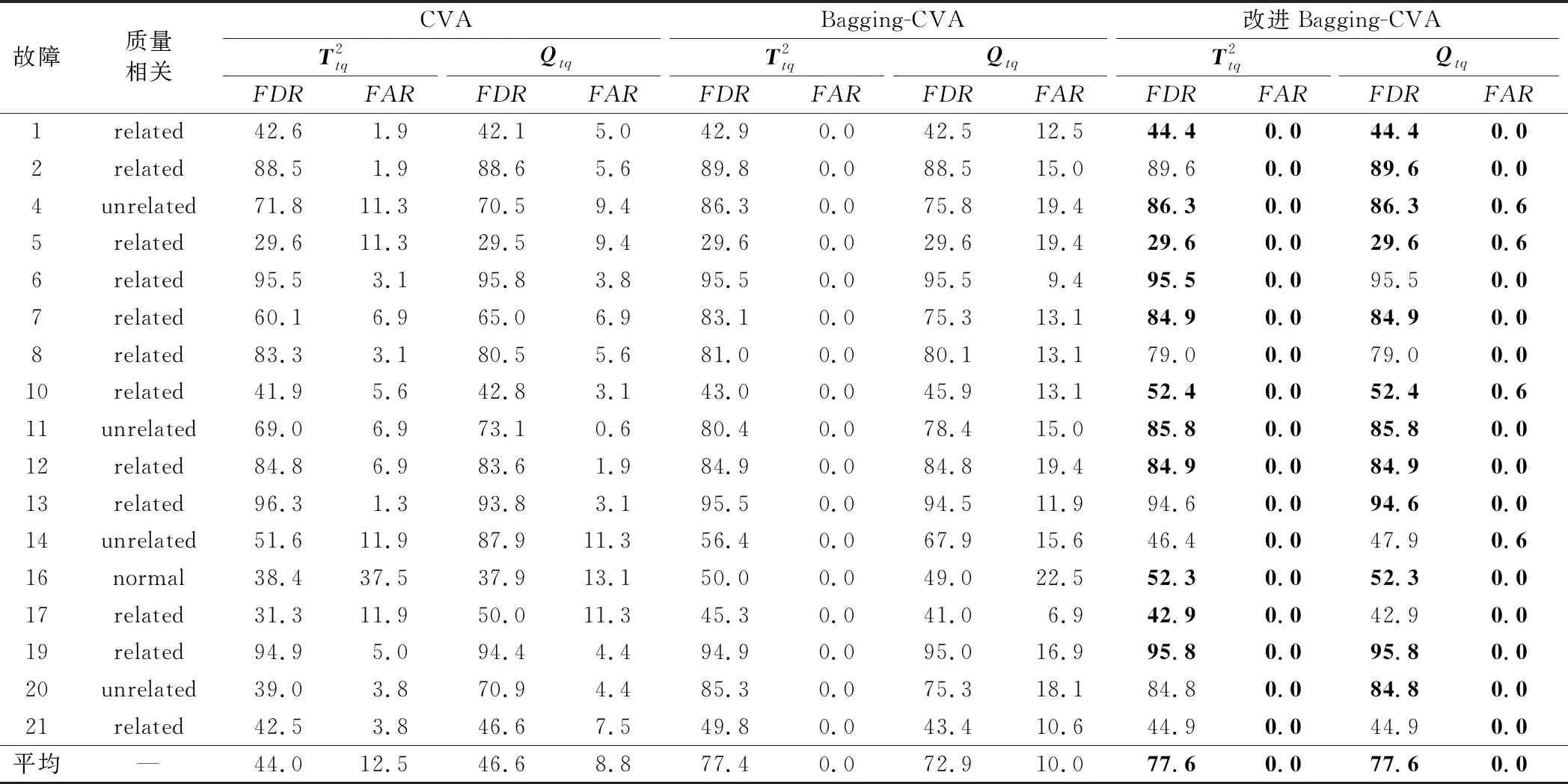
式中,fdrij為第i個模型的第j類故障數據的檢測率。對檢測率矩陣每列從大到小排序,計算前h行數值所對應的檢測率矩陣索引i(h 當最高檢測率模型和最低誤報率模型確定后,對相應統計量通過貝葉斯融合策略進行融合[17]。 定義樣本x在某一個模型中發生的概率為 (11) 式中,P(x|N)和P(x|F)分別為樣本正常與故障的后驗概率,計算公式如下: (12) (13) 式中,S為模型的統計量;S為控制限;P(F)為置信度α,則P(N)為1-α。融合后的統計量為 (14) 式中,融合后統計量BIC的控制限為置信度α;i為需要融合的模型個數,本文i值為2,即使用模型選取策略確定的最高檢測率模型和最低誤報率模型,減少了故障檢測采用多組模型融合的復雜度。 該算法分為離線建模和故障檢測兩個部分,如圖2所示。 圖2 基于改進Bagging-CVA方法的過程及質量相關故障檢測流程圖 (1) 離線建模。 ① 將過程數據集X和質量數據集Y進行z-score標準化處理為Xnew和Ynew。 ② 對Xnew和Ynew同步隨機抽樣形成多組數據集,分別使用式(5)建立過程檢測模型,使用式(7)和式(8)建立質量相關檢測模型,并通過2.2節方法確定最優的過程故障檢測模型和質量相關故障檢測模型。 ④ 采用核密度估計法確定各統計量控制限,置信度設置為95%。 (2) 故障檢測。 ① 采用離線數據對應的均值和方差對測試數據Xt進行標準化處理。 ③ 將各統計量分別按式(14)進行融合,其中使用離線過程的各最優模型統計量所對應的控制限。 ④ 判斷融合后各統計量是否超限,故障是否發生。 參考文獻[22]構造出一個具有動態過程和質量相關的仿真案例,其結構如下: (15) 其中過程數據X=[x1,x2,…,x10]T可以由X1=[x1,x2,…,x5]T和X2=[x6,x7,…,x10]T組成,x1~x5為質量相關的過程變量,x6~x10為非質量相關的過程變量。矩陣Y=[y1,y2,…,y5]T為質量數據集,y1~y5為質量變量。e~N(0,0.01)為高斯噪聲,系數W1、W2和Z分別為 矩陣R=[r,2r+1,r2-1,r2-3r,-r3+3r2]T,則變量r的計算方法為 r(t)=0.811r(t-1)+0.193ω(t) (16) 式中,ω為隨機變量,且ω~N(0,0.1)。 仿真實驗時,通過式(15)獲取樣本長度為1000的正常數據作為訓練集,并進行離線建模。再分別獲取2組數據用于模型校驗和故障檢測,每組數據包均有6個數據集,在第501個采樣點處引入故障,故障類型設置如表1所示。表中分別對不同故障的產生位置、發生方式、尺度以及是否與質量相關進行了設定。 表1 故障類型設置 圖3和圖4分別為故障1(質量相關故障)和故障6(非質量相關故障)的質量變量監視圖。圖3和圖4均給出了質量變量y1~y5的波動情況,通過分析可知,在第500個采樣點之后,質量相關的過程變量產生故障,質量變量波動情況異常。當非質量相關的過程變量產生故障時,質量變量則無明顯波動情況。 圖3 故障1的質量變量監視圖 圖4 故障6的質量變量監視圖 圖5 故障1的改進Bagging-CVA檢測結果圖 表2列出了6類故障檢測結果,其中FDR為檢測率(%),FAR為誤報率(%),AVE為均值,主元個數均為3。與傳統CVA方法進行對比(本文方法檢測效果挺高部分已加粗顯示),驗證了本文所提出的方法的有效性。在此基礎上,將所提出的方法應用于TE過程中,進一步驗證其有效性。 表2 故障檢測結果 TE過程已在故障檢測領域廣泛應用,詳細介紹可見文獻[23]。過程共有41個測量變量和12個控制變量。本文選擇測量變量XMEAS(1~35)和控制變量XMV(1~11)作為過程變量,測量變量XMEAS(36~41)作為質量相關變量。TE過程共設有21種故障,故障均從第161采樣時刻引入。使用本文方法對21種故障進行檢測,其中本文參數選取為B=1000,α=0.025,各模型主元個數分別按照累計貢獻率80%確定。對故障4(非質量相關故障)和故障7(質量相關故障)的檢測結果進行了具體分析。其余故障均列表給出,并與PCA、 CVA和Bagging-CVA方法進行了對比。 圖7 故障4的質量變量監視圖 圖8 故障4的改進Bagging-CVA檢測結果圖 通過工藝分析可知,故障7是組分C發生階躍變化,導致系統質量相關變量波動異常,由于系統閉環調節作用,500時刻之后質量相關變量基本恢復正常。故障7的質量變量監視圖如圖9所示,在第161個采樣點產生故障后,質量變量產生波動,第500個采樣點后質量變量又逐漸恢復正常,其質量統計量T2在此采樣點后也不再超限。 圖9 故障7的質量變量監視圖 圖10 故障7的改進Bagging-CVA檢測結果圖 改進Bagging-CVA方法以及對比方法PCA、CVA和Bagging-CVA方法的過程相關故障檢測結果如表3所示,詳細列出各方法對不同類型故障的檢測率和誤報率。因故障3、9、15為較難檢測故障,大多數基于數據驅動的方法檢測效果不佳[24],本文不再列出。表中改進Bagging-CVA方法的檢測效果提高部分已加粗顯示。通過對比分析,本文方法的平均檢測率和誤報率指標均要優于其他方法。質量相關故障檢測結果如表4所示,表4中給出了本文方法以及CVA和Bagging-CVA方法的數據對比。從表4中可以看出,改進Bagging-CVA方法的檢測效果要優于其他方法,特別是誤報率方面,幾乎沒有誤報的發生。通過表3和表4的數據分析,進一步驗證了本文方法的有效性。 表3 過程相關故障檢測結果 表4 質量相關故障檢測結果 本文提出一種動態過程及質量相關故障檢測方法,采用Bagging算法思想可以消除樣本間的時序相關性,并利用CVA方法分別建立過程相關故障檢測模型和質量相關故障檢測模型,在過程故障發生時可以進一步判斷此類故障是否影響產品質量。提出的最優模型選取策略,可以在離線建模時直接確定最優故障檢測模型,避免了傳統Bagging算法對多組模型的檢測結果進行融合的問題。通過仿真實驗并與PCA、CVA和傳統Bagging-CVA方法進行了對比,結果表明,在動態過程及質量相關故障檢測方面,本文方法的檢測能力均有一定程度的提高,驗證了方法的有效性。此外,CVA方法是常用的線性算法,而現實過程中往往具有很強的非線性,如何處理此類問題將是下一階段的研究重點。2.3 Bagging-CVA算法
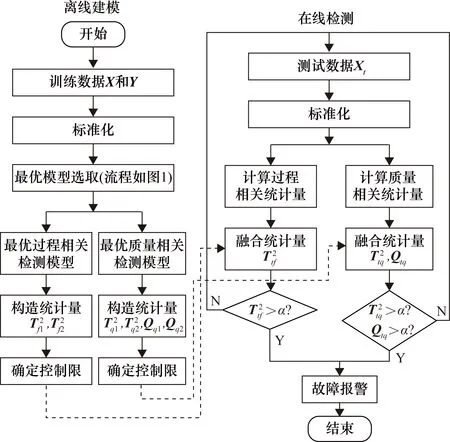
3 仿真研究
3.1 數值案例

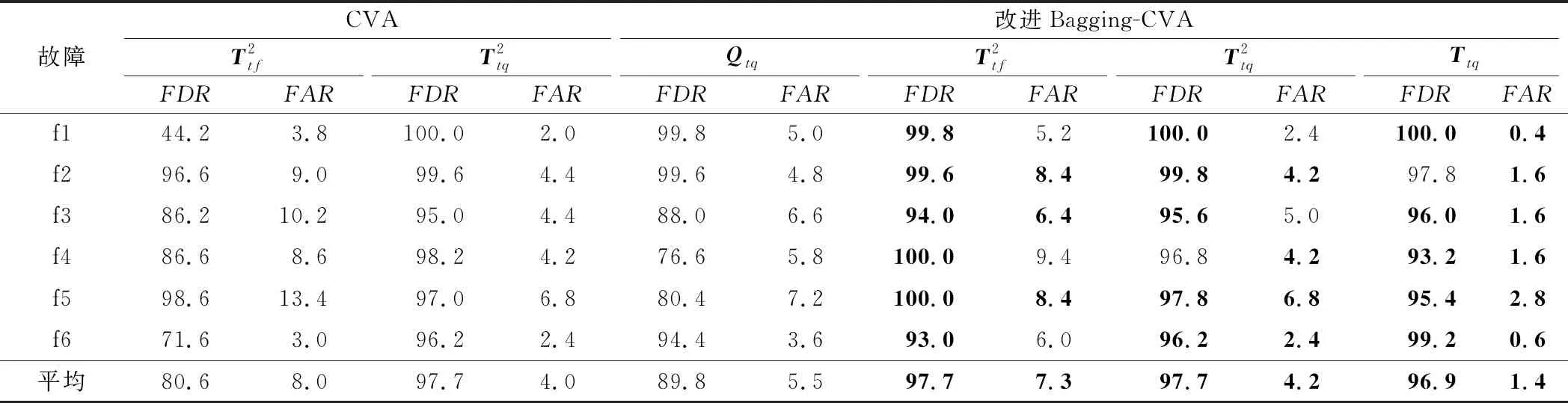
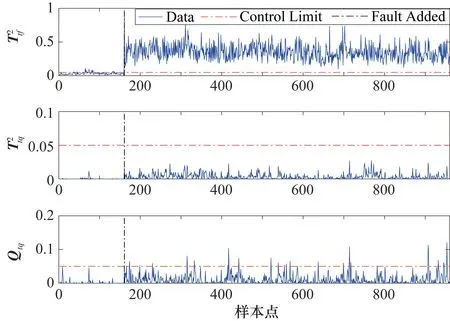
3.2 TE過程



4 結束語

