尺寸效應理論與模型及其應用

孟威 魯猛 王昊

摘 要：尺寸效應是指隨著結構尺寸的增大，以強度為代表的力學性能指標有規律地降低的現象。本文主要對目前使用較為廣泛的4種尺寸效應理論進行評述，進而闡述學者對不同材料進行的尺寸效應問題試驗。在當前尺寸效應理論的基礎上，對全尺寸試件的尺寸效應規律進行探討，并提出結合試驗研究以及數值分析模型進行對比驗證是今后研究者的重要研究方向。

關鍵詞：尺寸效應;Weibull統計尺寸效應理論;邊界尺寸效應理論

中圖分類號：TU528 文獻標識碼：A 文章編號：1003-5168（2021）19-0072-03

Abstract： Size effect refers to the phenomenon that the mechanical property index represented by strength decreases regularly with the increase of the size of the structure. In this paper， four kinds of size effect theories which were widely used at present are reviewed， and then the experiments on size effect of different materials conducted by scholars were expounded. On the basis of the current theory of size effect， it is an important research direction for future researchers to discuss the size effect law of full-size specimens， and to compare and verify it by combining experimental research and numerical analysis model.

Keywords： size effect;Weibull statistical size effect theory;boundary size effect theory

隨著當今社會工程建設的高速發展，混凝土、水泥砂漿和巖石等材料在工程結構建筑中的應用范圍也越來越廣。在該背景下，保證材料力學性能及結構安全系數滿足工程需求成為重中之重。隨著自密實混凝土、纖維混凝土、礦渣混凝土等一系列新型環保材料的出現，其材料參數的確定成為目前學者重點研究的方向。一般情況下，工程結構實際尺寸都超出實驗室的試驗條件，因此實驗室中通常在小尺寸試件上進行試驗來測定材料參數，導致得到的參數值存在一定的尺寸效應。為了得到準確的材料參數，眾多學者對尺寸效應問題進行了理論研究和試驗驗證[1]。本文介紹了4種使用較為廣泛的尺寸效應理論——Weibull統計尺寸效應理論、Bazant斷裂力學尺寸效應理論、Carpinteri多重分形尺寸效應理論、邊界尺寸效應理論，并結合學者針對不同材料進行的尺寸效應試驗，對各類材料的尺寸效應理論及適用性進行了簡單介紹[2]。

1 Weibull統計尺寸效應理論

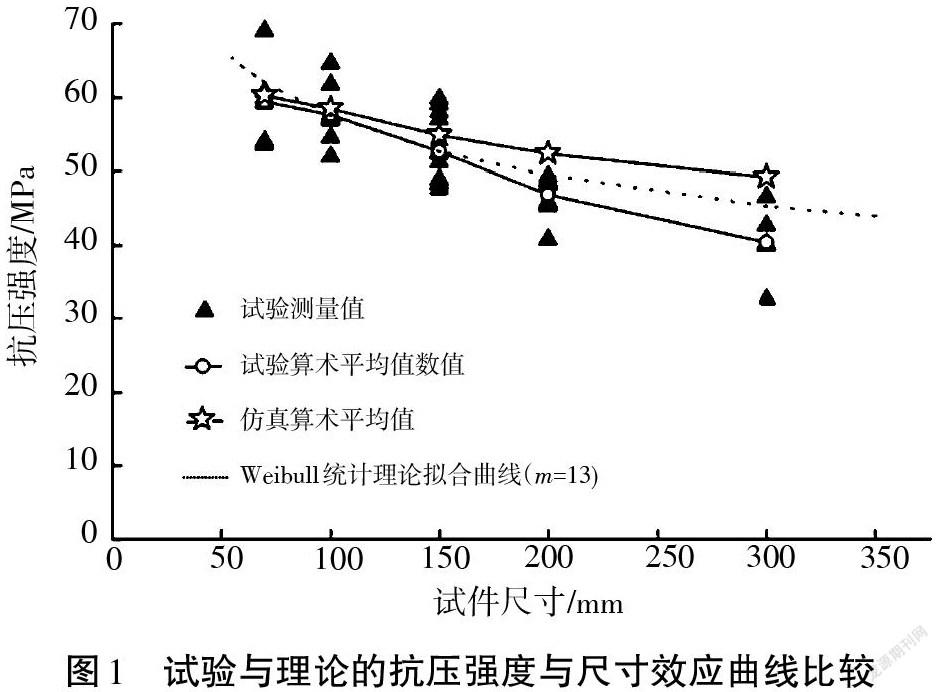
20世紀80年代以前，材料的失效一直將應力與應變作為評判依據，材料的尺寸效應問題幾乎沒有受到材料力學研究者的關注。這主要是因為力學理論學者認為，尺寸效應如果能被觀察到，就一定具有統計性，因此應由統計學家或實驗工作者進行統計研究。而隨著概率統計學在尺寸效應試驗研究中的應用，統計斷裂理論逐漸發展，并形成了概率斷裂力學。1925年，TIPPETT建立了極值統計理論。1926年，PERICE在此基礎上提出了鏈環強度模型。鏈環強度模型可以形象地描述為：設有一條由N個網類型環組成的鏈，兩端作用于大小相等、方向相反的力，只要其中一個環被拉斷，整個鏈條就被拉斷。把這種模型用在脆性結構時，可把結構看成由數目極大的若干單元串聯而成的，各個單元相互無關，若其中一個單元發生破壞，則整個結構發生破壞[3]。1939年，WEIBULL建立了強度統計理論，提出了用冪函數律描述強度極值分布律。Weibull統計尺寸效應理論[2]適用于在宏觀斷裂點失效的結構，且失效僅造成可忽略應力重新分布的一小塊斷裂擴展區[4]。張俊應用Weibull統計尺寸效應理論，試驗證明水泥砂漿、混凝土立方體雙軸抗壓強度具有尺寸效應[5]。何淅淅等應用Weibull概率分布假設來檢驗粉煤灰摻量對混凝土強度的影響，結果表明Weibull分布擬合效果較好[6]。唐欣薇等通過自密實混凝土試件單軸壓縮試驗，發現試件單軸抗壓強度呈現出明顯的尺寸效應現象，如圖1所示[7]。，根據Weibull強度統計理論得到的擬合曲線與試驗結果有良好的一致性，說明Weibull強度統計理論的正確性及合理性[7]。

2 Bazant斷裂力學尺寸效應理論

1984年，BAZANT基于裂縫帶模型建立了基于斷裂能釋放的斷裂力學尺寸效應理論[8-9]。BAZANT認為，混凝土和巖石的斷裂前沿被微裂紋區鈍化，韌性金屬的斷裂前沿被屈服區鈍化，會導致偏離線性彈性斷裂力學（LEFM）中已知的結構尺寸效應。Bazant斷裂力學尺寸效應理論認為，尺寸效應是由試件內部宏觀裂紋或微裂紋區的發展而產生的應力重分布和儲存的能量釋放引起的，即尺寸效應是由宏觀裂紋擴展時應變能耗散所引起的。

田穩苓和卿龍邦等采用預制缺口梁的三點彎曲試驗，證明水泥砂漿和亂向鋼纖維增強水泥砂漿的彎曲強度具有尺寸效應，而定向鋼纖維增強水泥砂漿的彎曲強度受試件尺寸的影響程度不明顯[10]。童谷生和吳秋蘭應用尺寸效應律擬合碳纖維增強水泥基復合材料的尺寸效應，得到碳纖維水泥砂漿棱柱體的電阻率、壓敏特性、軸心抗壓強度存在尺寸效應現象[11]。蘇捷和方志通過圖2[12]所示的抗壓試驗裝置進行不同強度等級立方體混凝土試驗，發現不同等級混凝土的抗壓強度均具有尺寸效應，且證明了尺寸效應律公式與試驗結果吻合較好，并得到了適用范圍較廣的混凝土抗壓強度尺寸效應律計算公式[12]。

3 Carpinteri多重分形尺寸效應理論

1994年，CARPINTERI基于經典固體力學中的分形自相似概念研究混凝土裂縫面的分形特性，建立了材料的斷裂特性與分形維數之間的數學關系式，確定了多重分形尺寸效應理論[13-15]。CARPINTERI提出，在尺寸效應對脆性和無序材料（混凝土、巖石、陶瓷等）抗拉強度和斷裂韌度的影響中，分形幾何概念應該被重點考慮，并應定義新的拉伸性能，這取決于無序材料或受損微結構不受尺寸影響的分形維數。CARPINTERI認為，只有在擁有非整數維數的分形空間內研究材料的尺寸效應問題，才能避免僅在理想整數維數空間內研究混凝土等無序結構材料產生的系統誤差。楊健男等應用Carpinteri多重分形尺寸效應理論，將廢棄纖維再生混凝土的試驗數據進行擬合，擬合效果良好[16]。

4 邊界尺寸效應理論

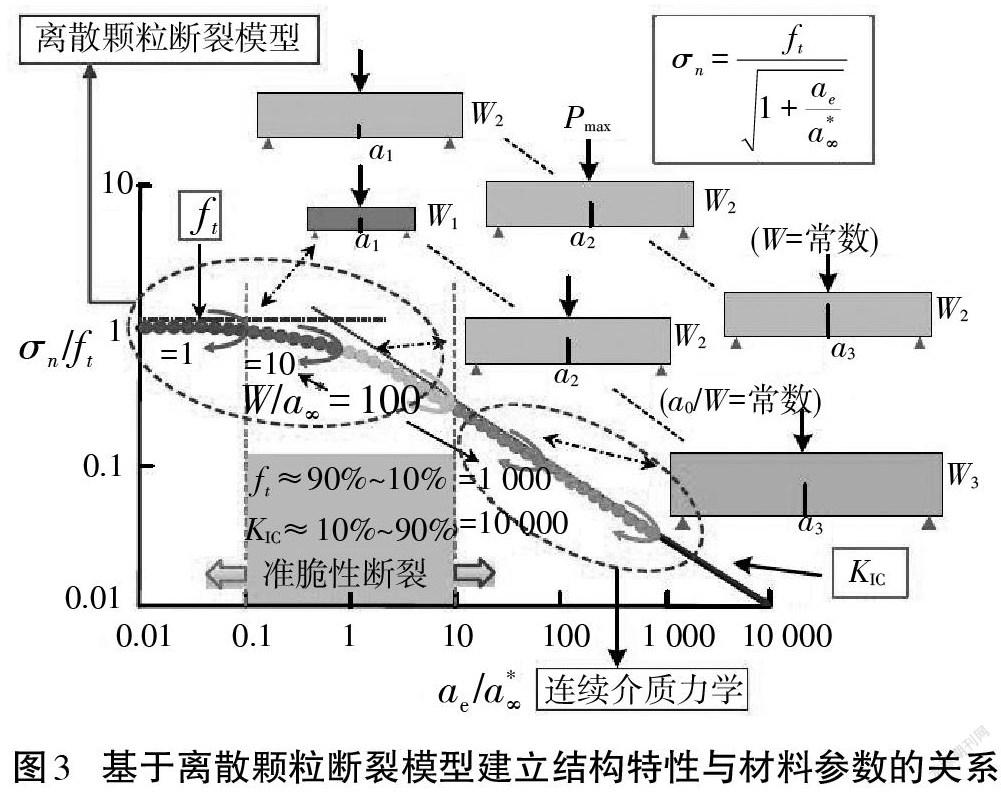
2000年，HU等基于邊界效應模型建立邊界效應理論，認為材料參數產生尺寸效應的根本原因不是試件尺寸發生變化，而是裂縫斷裂過程區與試件邊界兩者的相互影響[17-22]。邊界尺寸效應對幾何相似和非幾何相似試件都適用，且認為相對尺寸是影響尺寸效應的主要因素。基于邊界尺寸效應理論可確定材料參數，進一步可以建立描述結構斷裂破壞的預測設計曲線[11]，如圖3所示[23]。當[ae/a∞>10]時，結構破壞受控于斷裂韌度準則;當[0.1<ae/a∞<10]時，結構處于準脆性斷裂狀態，結構破壞同時受控于斷裂韌度準則與強度準則;當[ae/a∞<0.1]時，結構破壞受控于強度準則。

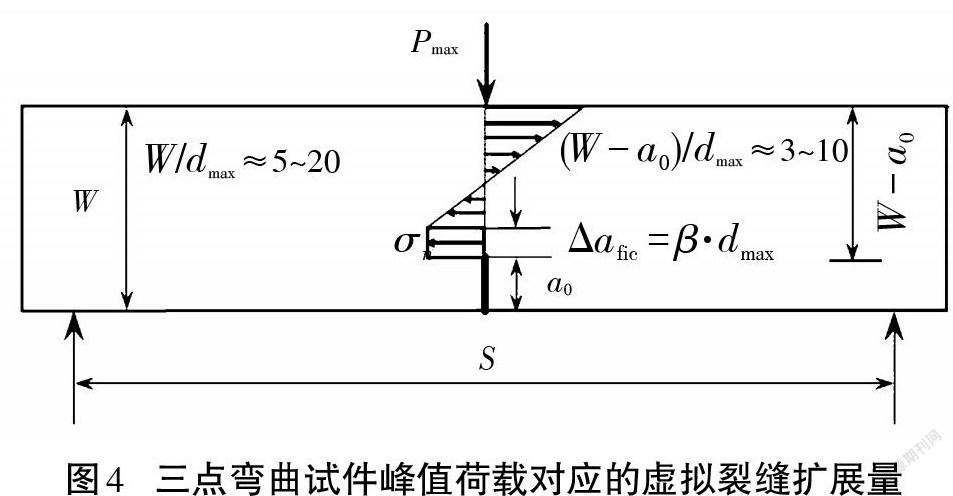
杜敏等通過楔入劈拉試驗，基于邊界效應理論模型得到了非幾何相似早齡期混凝土試件的斷裂參數[24]。管俊峰和胡曉智等引入巖石骨料最大粒徑，通過三點彎曲試驗證明在離散系數[β]=1.0的情況下，可以得到較為精確的材料參數，并能建立完整的巖石破壞曲線[25]。侯俊豪依據失穩斷裂韌度和等效斷裂韌度研究了骨料級配對邊界效應理論中[β]值的影響。結果表明，利用名義等效平均骨料粒徑計算平均骨料粒徑尺寸構建的邊界效應模型是合理的，能擬合出較為合理的斷裂韌度及抗拉強度[26]。管俊峰和王強等通過不同尺寸水泥砂漿試件的三點彎曲試驗（見圖4），將峰值荷載對應的虛擬裂縫擴展量與離散系數聯系起來，從而進一步研究水泥砂漿材料參數的邊界效應，并確定了無尺寸效應的材料參數，進而建立了完整的破壞曲線[27]。

5 結語

本文從理論分析和試驗研究兩個方面對尺寸效應進行了簡單介紹。目前，尺寸效應理論在混凝土、水泥砂漿、巖石等材料的力學性能測定應用上有了很大的成就，通過實驗室小尺寸試件試驗得到無尺寸效應材料參數的方法也逐漸成熟。因此，對大尺寸結構及試件的尺寸效應行為進行探討，構建用于測定材料力學性能的數值分析模型是今后的重要研究方向。

參考文獻：

[1]錢覺時，黃煜鑌.混凝土強度尺寸效應的研究進展[J].混凝土與水泥制品，2003（3）：1-5.

[2]杜修力，金瀏，李冬.混凝土與混凝土結構尺寸效應述評（Ⅰ）：材料層次[J].土木工程學報，2017（9）：28-45.

[3]徐世烺，趙國藩.混凝土斷裂韌度的概率模型研究[J].土木工程學報，1988（4）：9-23.

[4]王文標，黃晨光，趙紅平，等.結構破壞的尺度律[J].力學進展，1999（3）：383-433.

[5]張俊.混凝土與砂漿雙軸受壓性能尺寸效應試驗研究[D].長沙：湖南大學，2017：17-18.

[6]何淅淅，鄭學成，林社勇.粉煤灰混凝土強度統計特性的試驗研究[J].土木工程學報，2011（1）：59-65.

[7]唐欣薇，石建軍，郭長青，等.自密實混凝土強度尺寸效應的試驗與數值仿真[J].水力發電學報，2011（3）：145-151.

[8]BAZANT Z P，OH B H.Crack band theory for fracture of concrete[J].Materials and Structures，1983（3）：155-177.

[9]BAZANT Z P.Scaling of quasibrittle fracture：asymptotic analysis[J].International Journal of Fracture，1997（1）：19-40.

[10]田穩苓，馬林翔，卿龍邦，等.鋼纖維增強水泥砂漿彎曲強度的尺寸效應[J].混凝土與水泥制品，2015（9）：51-54.

[11]童谷生，吳秋蘭.碳纖維水泥砂漿柱體軸壓下力電性能尺寸效應研究[J].華東交通大學學報，2011（5）：46-51.

[12]蘇捷，方志.普通混凝土與高強混凝土抗壓強度的尺寸效應[J].建筑材料學報，2013（6）：1078-1081.

[13]CARPINTERI A.Decrease of apparent tensile and bending strength with specimen size：two different explanations based on fracture mechanics[J].International Journal of Solids & Structures，1989（4）：407-429.

[14]CARPINTERI A.Fractal nature of material microstructure and size effects on apparent mechanical properties[J].Mechanics of Materials，1994（2）：89-101.

[15]CARPINTERI A.Scaling laws and renormalization groups for strength and toughness of disordered materials[J].International Journal of Solids and Structures，1994（3）：291-302.

[16]楊健男.廢棄纖維再生混凝土強度試驗的尺寸效應[D].沈陽：沈陽建筑大學，2018：21-22.

[17]HU X Z，WITTMANN F.Size effect on toughness induced by crack close to free surface[J].Engineering Fracture Mechanics，2000（2）：209-221.

[18]HU X Z.An asymptotic approach to size effect on fracture toughness and fracture energy of composites[J].Engineering Fracture Mechanics，2002（5）：555-564.

[19]HU X Z，DUAN K.Influence of fracture process zone height on fracture energy of concrete[J].Cement and Concrete Research，2004（8）：1321-1330.

[20]HU X Z，DUAN K.Size effect：Influence of proximity of fracture process zone to specimen boundary[J].Engineering Fracture Mechanics，2007（7）：1093-1100.

[21]HU X Z，DUAN K.Size effect and quasi-brittle fracture：the role of FPZ[J].International Journal of Fracture，2008（1）：3-14.

[22]HU X Z，DUAN K.Mechanism behind the size effect phenomenon[J].Journal of Engineering Mechanics，2010（1）：60-68.

[23]管俊峰，姚賢華，白衛峰，等.由小尺寸試件確定混凝土的斷裂韌度與拉伸強度[J].工程力學，2019（1）：70-79.

[24]杜敏，武亮，張建銘.不同初始縫高比的混凝土斷裂試驗及邊界效應分析[J].水利水電技術，2019（11）：141-148.

[25]管俊峰，胡曉智，李慶斌，等.邊界效應與尺寸效應模型的本質區別及相關設計應用[J].水利學報，2017（8）：955-967.

[26]侯俊豪.利用邊界效應理論探究骨料級配對混凝土斷裂性能的影響[D].大連：大連理工大學，2019：16-17.

[27]管俊峰，王強，HU X Z，等.考慮骨料尺寸的混凝土巖石邊界效應斷裂模型[J].工程力學，2017（12）：22-30.

3590500338289