圍巖松動圈理論計算方法的評述與展望

劉 剛肖勇卓朱俊福靖洪文

(1.中國礦業大學 力學與土木工程學院,江蘇 徐州 221116;2.中國礦業大學 深部巖土力學與地下工程國家重點實驗室,江蘇 徐州 221008)

經過多年的理論發展和工程實踐,圍巖松動圈巷道支護理論在煤礦巷道設計與施工中起到了巨大的指導作用。以圍巖松動圈為指導,地下工程穩定性控制為目的的研究也越來越多,凸顯了準確計算松動圈厚度的重要性。圍巖松動圈是地下空間開挖后,次生應力使得圍巖發生變形和破壞,并在周邊一定深度區域內形成的破裂帶[1],其力學特性表現為內應力降低,物理特性表現為聲波速度降低。在20世紀50年代,拉巴斯提出松動裂隙學說并給出相應的計算公式,80年代池田和彥利用聲波法測試得出松動區計算方法,90年代E.L SHEMYAKIN 給出了松動圈與埋探、跨度、原巖應力、巖石強度等經驗公式[2]。對于松動圈的現場實測,宋宏偉利用地質雷達對松動圈進行測定[3],靖洪文等利用鉆孔攝像探測孔內裂隙發展給出判定松動圈厚度方法[4]。在數值計算方面,筆者采用ANSYS 模擬得出矩形煤巷圍巖松動圈的形成和發展機理[5],肖明等建立地下硐室開挖爆破三維彈塑性損傷有限元計算模型并根據圍巖損傷閾值系數分布確定松動圈范圍[6]。

由于小松動圈的形成需要3～7 d,大松動圈則需要幾個月甚至更長時間[1,7],因此松動圈的現場實測往往滯后于工程設計,而數值模擬的地質建模過程較為復雜,相對而言理論計算更為方便快捷,為工程設計和施工提供指導。筆者對基于巖石強度準則和數學模型計算松動圈厚度的相關研究進行論述,并對2種方法計算過程的關鍵問題進行分析,指出2 種方法的工程應用條件和未來研究的展望。

1 巖石強度準則法

巖石強度準則計算松動圈厚度的基礎是靜水應力作用下軸對稱圓形巷道模型的彈塑性應力狀態分析[8](圖1)。后續學者結合Mohr-Coulomb 準則(簡稱M-C 準則)、Hoek-Brown 準則(簡稱H-B 準則)和Druker-Prager 準則(簡稱D-P 準則)等準則與靜力平衡方程等條件逐步推導出軸對稱圓巷的塑性區及松動圈半徑公式。

圖1 軸對稱圓形巷道模型Fig.1 Model of axisymmetric circular roadway

1.1 基礎準則推導

1.1.1 Mohr-Coulomb 準則

在M-C 準則基礎上最先推導出軸對稱圓巷的塑性區半徑Rp,即卡斯特納(H.KASTNER,1951)方程,或稱修正芬納(FENNER)方程[8],即

其中,R0為巷道半徑;p0,p1分別為原巖應力和支護反力;c為黏聚力;φ為內摩擦角。塑性區半徑的推導為松動圈厚度的推導奠定了基礎,后續研究需要根據邊界條件來區分松動區與塑性區。

文獻[9]根據應力平衡方程、M-C 準則和內邊界處徑向應力等于支護反力得出破裂區(即松動區)應力,結合前人推導的塑性區應力方程,通過建立符合M-C 準則的塑性勢函數,利用非關聯流動準則得出了破裂區和塑性區的應變分布,然后根據破裂區與塑性區的環向應力連續條件與徑向應變連續條件對上述應力應變方程求解得出松動圈厚度。因此,計算松動圈厚度首先需要推導松動區和塑性區的應力分布,而是否建立應變分布方程在于松動圈邊界條件的設定。一般情況下,實驗室獲得的巖石力學參數與實際巖石工作狀態時有較大出入,需要引入其他理論對相關參數進行修正。

損傷理論引入巖石力學后為松動圈的研究提供一個新的思路。文獻[10]引入雙直線損傷模型,即將巖石全應力應變曲線簡化為雙直線型,損傷演化方程為

式中,D1為損傷變量;εc,ε分別為巖石全應力應變曲線峰值點的應變、軟化階段任意點的應變;λ為峰值后線性軟化階段的降模量,λ=ηE(1-β2);η為巖石破壞前積累的形變能與損傷破壞后所釋放的能量比;β為殘余應力與峰值應力的比值;E為彈性模量。

文獻[10]在損傷區對黏聚力進行折減,設定松動區與塑性區邊界上切向應力σθ等于原巖應力p0,初步計算出損傷區半徑。通過令損傷區內切向應力等于巖石的殘余強度σu或降低損傷變量D1獲得完全損傷區半徑,完全損傷區內巖石失去承載能力,認定其半徑實際為松動圈厚度。相比于巖石強度未弱化情況,利用損傷理論軟化巖石所得到的松動圈厚度更接近實測值。但根據巖石的全應力應變曲線和圍巖四分區(即破碎區、塑性軟化區、塑性硬化區和彈性區)研究[11-12],破碎區和塑性軟化區共同組成破裂區(即松動圈區域),故計算所得的松動圈厚度值小于實測值,其計算結果目前只能作為定性參考。

1.1.2 Hoek-Brown 準則

1980年提出的H-B 準則得到了巖石力學界與工程研究者的廣泛認同。H-B 準則自提出后得到了多次修正,以2002年HOEK 和BROWN 修正后的準則(即廣義H-B 準則)應用最為廣泛[13],修正后的準則為

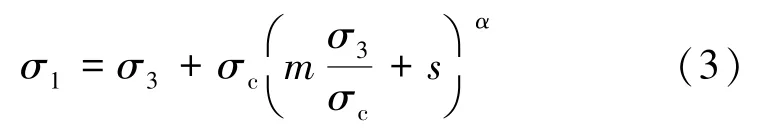
式中,σc為完整巖石試件的單軸抗壓強度;m,s和α均為H-B常數,m=mie(GSI-100)/(28-14D),s=e(GSI-100)/(9-3D),;mi為完整巖石的H-B 常數,由巖石種類決定;D為擾動系數;GSI為巖體的地質強度指標。

后續學者將該準則引入圍巖松動圈的研究中。文獻[14]利用應力連續條件以及彈塑性區交界面處的彈塑性區內徑向應力與切向應力之和等于2 倍的原巖應力,初步計算得到松動區半徑公式;文獻[15]在利用廣義H-B 準則研究松動圈時分別給出了經驗法、實驗法和野外確定H-B 常數m和s的方法,并給出根據修正GSI 法評估兩個常數的的方法;文獻[16]則考慮中間主應力σ2的影響引入洛德參數(其中σ1,σ3為巖體破壞時的第1、第3 主應力)來研究塑性區問題,設定松動區與塑性區邊界條件與文獻[10]相同。

文獻[17]指定松動區內廣義H-B 常數α為0.5,為了進一步軟化巖石強度以準確計算松動圈厚度,作者基于可拓學理論利用熵權法建立了考慮爆破損傷情況、卸荷情況、巖體完整性指標、圍巖級別4 因素的物元模型,從而準確計算影響H-B 常數m和s的擾動因素D的數值。文獻[17]給出了影響巖石強度次要因素的計算方法,但計算過程中的4 因素數值均需要結合經驗人為給定,這樣會使計算過程更為復雜化,結果也容易產生較大偏差。由于文獻[14,16-17]均設定相同的彈塑性邊界條件,故推導的松動圈半徑實際上仍為塑性區半徑。

1.1.3 Drucker-Prager 準則

D-P 準則于1952年提出,廣泛用于巖土力學與工程的數值計算方面。該準則考慮了中間主應力σ2對巖石整體受力的影響,其式為

式中,I為第一應力不變量;J2為第二應力偏量;k,α′為D-P 準則系數,其值分別為

文獻[18]將基礎的圓巷模型簡化為平面應變厚壁圓筒問題,在該準則基礎上初步計算得到塑性區半徑及塑性區內應力。文獻[19]推導過程借鑒了文獻[9]的思路,引入了塑性區擴容系數即塑性區最小塑性主應變增量與最大塑性主應變增量之比分析各區的應變和位移,得出了在一定范圍內提高中間主應力系數m′(m′=(σ2-σ3)/(σ1-σ3))可有效控制圍巖變形及塑性區的擴展。不過文獻[19]后續利用控制變量法逐一分析該準則與M-C 準則、統一強度準則和雙剪強度準則中不同參數對圍巖應力、變形及塑性區、破裂區范圍的影響,未能與實測松動圈值進行驗證。同時文獻[19]未能對巖石強度進行軟化,使得上述分析存疑。

文獻[20]采用文獻[10]類似方法引入損傷力學一維線性演化方程實現對巖石強度的軟化,與文獻[10]不同的是峰值后損傷方程中的損傷變量D1=,其中降模量λ=E(2.5σc-0.15-1)-1,并在損傷區內對I和J2進行修正,實現對巖石的軟化,使計算結果更接近實測值。文獻[20]認為由于未考慮外界條件等因素對巖石軟化的影響和理想的彈塑性條件限制下,損傷區的值相對實測值偏小。而文獻[20]未采用文獻[10]的方法研究完全損傷區,但完全損傷區的研究對松動圈意義重大,適當修正文獻[10]中的殘余應力或損傷變量可以使得完全損傷區包含塑性軟化區,從而彌補因未考慮爆破等因素造成的影響。

1.2 邊界條件與巖石軟化

基于上述3 種強度準則準確計算松動圈厚度必須經歷3 個步驟:①求取該強度準則情況下塑性區的半徑;②區分塑性區與松動區;③對原有巖石強度準則進行修正,軟化巖石強度參數。3 個步驟并不一定區分先后順序。由此衍生出2 個主要難點:①塑性區與松動區交界處的邊界條件;②軟化巖石強度的方法。

1.2.1 邊界條件

破裂區與塑性區在交界面邊界條件需設置兩個才能對方程進行求解,一個是應力連續邊界條件,而另一個條件是區分塑性區和破裂區關鍵。該條件主要采用2 種方法:一是參考文獻[21]研究認為松動區內切向應力小于或等于原巖應力(邊界處取等號求解);另一種是根據塑性區與破裂區交界處徑向應變相等原則求解。相對于第1 種方法,第2 種方法是在巖石的全應力應變曲線分析的基礎上建立的塑性應變求解法,更具有說服力。除了上述2 種方法,文獻[22]通過巖石全應力應變曲線研究中提出松動圈內部破壞呈現出梯度特征,初步建立了巷道圍巖應力梯度破壞理論模型,為區分塑性區與破裂區提供新的思路。

1.2.2 巖石軟化

巖石從圍巖體取出并運至實驗室測試力學參數過程中已被擾動,其強度已不再是其工作狀態下的強度,需要對其力學參數進行修正。由于可以利用數學模型評估各影響因素對原巖強度的影響,H-B 準則相對其他準則具有自身優勢。M-C 準則和D-P 準則常采用損傷理論對準則中的參數進行修正實現巖石強度軟化,除了上述采用的損傷軟化方法,研究者采用軸向應變描述巖石微元強度,并利用巖石微元強度服從Weibull 分布的特點,建立了基于M-C 準則[23]、H-B 準則[24]等統計損傷理論。

因擾動因素的影響,工作狀態下巖體力學參數的準確測定相較于松動圈測定更困難,而圍巖位移是巖石在工作狀態下強度對抗圍壓的結果,后續研究者提出了根據位移量和松動圈實測值反演獲取工作狀態下圍巖的部分力學參數。文獻[25]將圍巖位移量分為未開掘前的彈性變形UE、爆破瞬間產生的彈性變形Ue和開掘后的塑性位移UP,并設定巖石服從M-C準則,根據實測爆破松動圈范圍建立數值模型,利用UE反演計算出原巖的彈性模量和泊松比以及側應力系數,在此基礎上利用UP和Ue分別反演得到松動圈范圍內圍巖的變形模量和泊松比、黏聚力和內摩擦角。后續研究中,有學者采用信息傳遞平臺的主從式并行PSO 算法耦合有限元彈塑性模型加快反演計算速度[26]或利用破壞擴展卡爾曼濾波器同離散元耦合建立反映巖土體動態隨機過程的反分析方法[27]。由于該方法反演的圍巖參數有一定波動,并與實測值有出入,可作為松動圈厚度計算的驗證。

1.3 其他準則

除了上述3 種常用準則推導松動圈厚度,研究人員也嘗試從多角度和多準則方面進行推導。文獻[28]雖基于M-C 準則,但求解時利用動靜力學方法,并認為松動區是由巷道圍巖的瞬時卸壓造成彈性波對圍巖的動力作用形成的破碎區和原巖應力作用下圍巖形成的塑性軟化區組成。從動力學角度分析彈性波作用下巷道圍巖的應力應變場,并設定拉應變達到極限拉應變作為巖石破壞條件,即破裂區與塑性軟化區的邊界條件從而求得破裂區半徑。但該文仍是基于塑性區公式Rp=R0×求得松動圈厚度;文獻[29]采用改進的雙剪統一強度準則[30],設定破裂區與塑性區邊界黏聚力等于殘余黏聚力以及位移與應力連續條件獲得松動圈厚度公式;文獻[31]結合MC,D-P、統一強度和Mogi-Coulomb 等4 個準則構建統一準則,以中間主應力系數取值選取準則,并根據大量試驗與實踐建立了黏聚力和內摩擦角的軟化模型,借鑒文獻[11]的推導過程得到松動圈半徑。由于各個準則自身應用范圍并不廣泛,且部分準則的優點并不突出,故在松動圈計算中較少應用。

2 數學模型法

理論計算圍巖松動圈的方法除了采用巖石強度準則推導外,基于已知的松動圈影響因素,利用數學模型計算各因素對松動圈的影響程度求取松動圈厚度的方法也較為常用。

2.1 常用數學模型

普遍認同的松動圈影響因素中,圍巖強度和地應力是松動圈的主要影響因素[32-33]。數學模型中圍巖強度常采用巖石單軸抗壓強度σc,地應力常采用原巖垂直應力σv,但原巖垂直應力的測量較難。已有研究表明,原巖垂直應力的大小與埋深H呈現一定的關系[34-35],同時研究表明松動圈與埋深一定程度上相關[36],故在不少數學模型研究中均采用埋深代替原巖垂直應力。松動圈次要影響因素包括了巷道跨度B、節理裂隙發育程度F、爆破損傷以及跨高比ζ等因素,這類因素對松動圈的影響較小,一定程度上影響松動圈的計算精度,但實踐證明對工程設計和施工并無決定性影響[1]。基于上述因素分析,研究者利用數學模型計算松動圈厚度主要采用了神經網絡模型和支持向量機模型。

2.1.1 神經網絡模型

神經網絡模型自20世紀40年代提出,后續不斷引入新的函數模型進行改進,其應用于松動圈預測較早。網絡結構普遍采用BP 神經模型,訓練樣本集{(xi,yi),i=1,2,…,k},其中xi∈Rn(i≤k)為多個松動圈影響參數數據,yi為每組松動圈影響參數對應的松動圈厚度值。利用大量的影響因素參數數據與松動圈實測值對數學模型進行訓練,獲取松動圈與影響參數之間的關系。模型的影響因素基本選擇了H,σc,F和B等4 項因素,樣本數據大多數來源于文獻[37]提供的平頂山礦區的16 個樣本模型。

后續研究者關注如何快速擬合逼近實測值,文獻[38-39]均利用了遺傳算法優化尋找BP 三層前饋神經網絡的權值和閾值的過程,兩者區別在于遺傳算法中適應值函數的構建,而文獻[38]采用改進后的遺傳算法在樣本數據較多及影響因素較多時更能快速逼近。文獻[40]采用基于變步長的最小二乘的方向傳播算法的自適應神經模糊推理模型擬合逼近實測值,同時也承認樣本數據存在一定“噪聲”,輔以核對數據庫修正后才進行數據訓練。文獻[41]則采用了以徑向基(高斯)函數K(xi,xj)=exp(- ω‖(xi -xj‖2)(ω為核函數的參數寬度)作為激勵函數的RBF 前饋神經網絡,相對于BP 模型能夠更快的局部擬合逼近松動圈實測值。

2.1.2 支持向量機模型

支持向量機模型于1995年提出,其回歸分析模型被應用于松動圈厚度的預測[42]。通過將訓練樣本數據歸一化后,以徑向基(高斯)核函數轉化至高維特征空間使數據線性可分,根據一定的算法尋找適應的懲罰參數δ和核函數參數ω后再進行訓練和回歸預測。該模型回歸預測松動圈的重點在于支持向量機模型的δ和ω尋優。

文獻[43]采用最小二乘線性系統作為損失函數代替支持向量機所采用的二次規劃方法提高模型的訓練速度,并利用基礎粒子群算法尋優,文獻[44-45]則分別采用了引入壓縮因子修正的粒子群算法和分層人工魚群算法進行尋優。文獻[46]則是在Libsvm 軟件的基礎上結合Python 調用Gnuplot 程序對δ和ω兩參數自動尋優,提高了模型運行速度和預測精度。支持向量機模型中采用的影響因素除了與神經網絡模型相同的4 項外,同時引入了巷道面積S[43,46]、直接頂與煤層厚度比ξ[43]等。上述文獻經對比后認為支持向量機模型的松動圈擬合結果的誤差小于神經網絡模型。已有的研究表明,支持向量機做非線性回歸時能避免神經網絡訓練結果不穩定的缺陷,同時能得出唯一的回歸解析式,而非神經網絡模型的黑箱函數。

2.1.3 其他模型

應用于松動圈計算的數學模型最早采用的是灰色預測模型,文獻[47]在內插法處理松動圈數據基礎上采用非等距時空的GM(1,1)模型預測,文獻[48]在此基礎上通過刪去最早的松動圈數據,使序列等維,更加反應系統的發展趨勢,提高長距離的預測精度。采用該模型預測松動圈時僅需要4 個及以上的松動圈數據,利用巷道掘進工作面附近松動圈變動規律預測前方松動圈,不需要檢測各項影響因素,若松動圈變動規律并不明顯,其預測長距離時的松動圈與實測值的誤差較大。故利用灰色預測模型預測松動圈的研究漸少,但其他領域對灰色預測模型的改進仍在繼續,在松動圈預測領域仍具有繼續開發的潛力,如何提高其長距離預測時的精度成為主要問題。

除了上述較早應用松動圈預測的數學模型,后續新引入了未確知聚類法[49]和量綱分析[50]等方法。文獻[49]將松動圈厚度分為大、中、小3 類,由此將樣本H,σc,F,S(巷道斷面面積)和B的數據范圍分類,建立起預測各因素的單因素未確知測度函數,并根據信息熵理論計算出各因素與松動圈之間的權值和多因素綜合未確知測度,以未確知測度距離預測對象松動圈所屬的分類等級,以樣本松動圈厚度的均值計算松動圈厚度的預測值。該方法在分析各因素與松動圈關系的同時,對單因素進行分類分析,但在樣本較少的情況下,部分接近分類邊界的因素值容易出現誤判,而該文也提到存在部分樣本預測值與實測值誤差較大的情況。

文獻[50]在系統分析松動圈影響因素的基礎上,新引入了上覆巖石容重γ和最大水平應力σHmax,借助量綱分析推導出松動圈厚度與6 個影響因素的初步關系式,對比4 種多元回歸擬合函數結果,得到對樣本數據擬合效果最好的多元冪函數公式。該方法采用理論推導與數學模型相結合,相對于普通的多元回歸函數擬合而言,能夠更快更高效的尋找到擬合效果最佳的函數關系式,但量綱分析過程影響因素的選擇限制其誤差精度的提高。

2.2 因素選擇與建模選型

綜合上述文獻,除灰色預測模型外,松動圈預測模型關鍵在于因素選擇和建模選型。因素選擇的重點集中在次要因素,而建模選型在于引入其他模型對原有模型的核心元素進行尋優。

筆者認為松動圈影響因素可概括為圍巖強度和圍壓。圍巖強度以次要因素中的節理裂隙發育程度、地下水、巖層厚度、溫度及爆破損傷等影響巖石單軸抗壓強度的取值;圍壓以地應力、側應力系數、巷道形狀、跨高比、跨度等影響其取值。次要因素的選擇是提高松動圈預測精度的關鍵,但在不同的地質情況下形成的巖石受不同因素影響且影響程度也各不相同,解決該問題的關鍵在于模型庫,而現有的模型庫涉及的影響因素較少,數據取值也有異議。建議各礦區、各煤礦分別建立圍巖參數和實測松動圈的數據庫進行數據共享;另一種解決辦法是采用灰色預測模型,但該方法波動性太大,準確度具有概率性。

當前用于預測的基礎數學模型已定型并在此基礎上不斷發展出優化模型。松動圈預測優化模型主要集中在提高擬合速度和精度,以遺傳算法和粒子群算法為主。遺傳算法擬合時比較均勻地向最優區域移動,同時能預估收斂速度;粒子群算法擬合是跟隨當前最優解進行搜索,擬合速度快但存在陷入局部最優等問題,但優化模型的改進也在不斷進行,如文獻[44]的改進模型可避開局部最優的缺點。模型選型主要是彌補數據庫數據不足以及樣本數據存在噪聲等問題。采用何種預測模型不再是重點,改進預測模型以適應數據庫才是松動圈預測的關鍵。預測模型的改進不局限于松動圈預測,如文獻[51]將支持向量機模型核函數改換為Morlet 小波K(xi,xj)=,并利用粒子群算法改進從而提高巖土參數反演精度。因此后續研究應關注數學模型在各行業的應用,從而將改進的數學模型服務于松動圈預測。

3 工程應用與展望

上述研究的松動圈計算方法各有優缺點,若要應用到實際工程中,則需要分析工程實際情況,對比各類方法的優缺點,選擇合適的計算模型。

3.1 工程應用

3.1.1 強度準則法

由于強度準則法推導松動圈的基礎是軸對稱圓巷,受其假設條件的限制必定與實測值存在出入。目前,理論解析方法僅能解一般的圓形巷道[8],而煤礦巷道多為梯形、矩形或直墻拱形等折線形斷面,巷道當量半徑R0的取值將對計算結果產生較大影響。對于馬蹄形斷面巷道當量半徑可采用R0=[(B/2)2+ h2]/(2h)(h為巷道實際高度)計算[52],但矩形巷道當量半徑難以計算。另外,假設條件中水平應力σh等于垂直應力σv,實際工程中存在這一情況,即側應力系數為1.0。而水平應力大于垂直應力的現象較為普遍,側應力系數的選取也將增大計算結果與實測值的差值,適當地實測σh和σv,有利于計算模型的正確選擇。假設條件中圍巖為均質巖石,一般情況下開挖影響范圍內會有多種巖層,不同巖性的巖石在相同應力下發生的狀態變化會造成應力分布不均,這一影響因素造成的誤差無法避免。除以上3因素外,文獻[17]建立數學模型定量評估了次要因素對巖石的弱化程度,其余文獻的理論公式中卻少見,在松動圈理論計算主體已確定的情況下,提高松動圈預測模型精度的關鍵在于次要因素。上述缺陷決定了強度準則法在非圓巷、水平應力與垂直應力相差大、次要因素影響較大等情況下計算所得松動圈與實測值相差較大,而圍巖巖性則決定了幾種強度準則法的適用性。

3.1.2 數學模型法

數學模型法的適用范圍很廣,其預測精度受制于影響因素的選擇和現有數據庫的大小。影響因素中的部分因素可以通過初步評估進行弱化或近似處理,如將巖石試件用礦井水軟化再測試其力學參數后可不考慮地下水影響,馬蹄形巷道采用當量半徑代替跨度可不考慮跨高比的影響等。在上述模型中均采用了埋深代替地應力,但已有數據表明,不同區域的地應力與埋深之間關系并不相同,部分區域甚至相差很大[34-35]。因素的選擇需要因地制宜,在綜合評估因素影響后再進行近似或消去部分次要因素。

雖然通過異地數據庫對本地松動圈計算時可以通過優化或改變數學模型提高擬合精度,但未經過大量的本地數據檢驗使其真實精度存疑,同時各個數學模型本身存在一定缺陷,若出現局部尋優擬合效果最佳,就更易造成模型出錯。因此建立本地松動圈及影響因素的數據庫越顯重要,而在本地數據庫缺少和因素影響程度不確定時不建議采用數學模型法。

通過以上分析發現,2 種研究方法對非規則形狀松動圈的研究較少。根據文獻[53-56]的研究,非圓形等不規則形狀松動圈的產生主要由于以下3 個因素:①巷道斷面形狀,矩形巷道松動圈明顯區別于圓形及近似圓形巷道;②側應力系數,文獻[55-56]對側應力影響圍巖應力分布的研究表明了松動圈的非規則形態受側應力系數影響顯著;③非均質巖層,特別是層狀巖層。而文獻[5]采用數值模擬的研究表明,中小松動圈受巷道斷面形狀影響,而大松動圈最值,但變動幅度不宜過大,否則應在模型中引入該未終趨于圓形。

文獻[53]采用保角變換和復變函數彈性理論得到矩形巷道圍巖應力及位移的彈性解析解,基于MC準則設定安全系數θ=作為巖石破裂條件,得到側應力系數為0.3 時的裂隙區分布,但實質上并不是松動圈分布。文獻[54]采用隧洞圍巖應力復變函數分析法中的解析函數通式和單位圓外域-洞室外域共形映射函數計算方法對矩形巷道孔邊應力計算,并認為側應力系數和跨高比對巷道孔邊應力影響顯著。文獻[55]采用文獻[53]方法,其保角變換的公式不同,得到另一圍巖應力解析解,同時對不同側應力系數和跨高比情況下的邊界應力進行分析,認為其呈現蝶形分布,符合松動圈實測和數值模擬結果[5]。矩形巷道中跨高比與側應力系數對矩形巷道松動圈的影響較大,然而在相關的數學模型中鮮有文獻引入上述2 個指標。文獻[56]采用多項式擬合回歸得到了矩形巷道松動圈厚度與多因素(包含跨高比)的關系式,但該關系式的相關性系數較小,相應的預測精度將會偏低。故現有的矩形巷道松動圈理論計算公式仍難以運用到工程中。

3.2 展 望

松動圈理論計算的目的是指導地下工程的設計與施工。作者在全國多個礦區采用超聲波測試儀、RAMAC 探地雷達、鉆孔攝像方法以及多點位移計方法等對松動圈進行現場實測中發現,受眾多因素影響,巷道同一橫斷面、同一巷道相鄰地段的松動圈均在一定范圍內波動,波動范圍小至幾厘米,大至50 cm 左右。在地層條件變化劇烈區域,松動圈波動范圍更大。圖2為某礦采用地質雷達測試的圍巖松動圈圖,其雷達圖像及測試數據往往不是理想的狀態,對雷達圖像及測試數據的處理,往往需要結合測試和分析者的經驗,因此具有一定范圍的主觀可變性。

因此,受地質條件和實測地質參數的不確定性影響,必須承認任何松動圈理論計算方法均并不能準確預測松動圈的大小。而隨著巷道掘進距離的增加,松動圈的波動范圍將會增大,先前準確計算的松動圈值與某段巷道實際松動圈均值的誤差也將增大。同時在單個松動圈計算模型不能全面考慮所有影響因素的情況下,未知因素必然影響已知因素,從而根據經驗判斷未知因素對哪些已知因素進行了正或負影響以及影響程度的大小,建議可一定范圍變動已知因素知因素,從而獲取某段巷道松動圈變動范圍,以提高設計與施工的安全性。

圖2 某煤礦圍巖松動圈雷達探測Fig.2 Radar chart of broken rock zone of a mine

由于對破裂區巖石破壞后的性質認識還不允分,現有計算理論的一些基本假設與實際圍巖的狀態有較大差距,準確計算松動圈厚度極為困難。對工程應用而言,強度準則法和數學模型法需要在多種地質狀況下保證一定精度。對于強度準則法,隨著煤礦逐漸向深部發展,由地應力引起的巖石蠕變加劇,已有的準則并不能很好地適應這種情況,需結合全應力應變曲線對松動圈進行計算,如文獻[57]提出的鹽巖蠕變模型、文獻[58]建立的基于三軸極限峰值偏應力的巖石非線性破壞強度準則。因此基于新的強度準則計算松動圈厚度將是松動圈理論研究的重點。對于數學模型法,因數據存在噪聲和模型本身存在的缺陷,單個模型預測結果穩定性不足,結合多種數學模型進行組合預測,提高模型在多種情況下的綜合精度和廣泛使用度,另一方面則是數據的等維信息,結合現場實測數據對數據庫進行更新。

除此之外,非規則形狀松動圈的相關研究相對匱乏,其支護問題更顯復雜,基于矩形巷道圍巖應力分析推導各準則情況下的矩形及非規則形狀巷道的松動圈更應成為松動圈研究的重點。

在產生了明顯松動圈的地下工程中,彈塑性力學等處理小變形問題的連續介質力學的分析方法,不能用于巖石強度峰值后區的破裂巖體,否則計算結果將產生較大誤差。目前進行這方面的研究主要采用數值模擬方法,或者實驗力學方法,而且仍在不斷發展。因此,在目前的工程應用中,如果難以符合強度準則法的假設條件及未知的次要因素影響程度較大的情況下,不建議采用計算的方法確定圍巖松動圈的值。

4 結 論

(1)基于巖石強度準則計算松動圈厚度,經歷了塑性區和松動區半徑公式推導、區分塑性區與松動區以及對巖石強度參數修正,總結了2 種區分塑性區與松動區的方法和對巖石軟化的方法,對應力梯度模型區分松動區與塑性區以及參數反演法修正巖石強度進行展望。

(2)基于影響因素分析計算松動圈的數學模型法,以因素選擇和建模選型為重點,總結了當前常采用的影響因素類型和多種數學模型的關鍵參數的尋優算法,指出預測模型精度提高的關鍵在于次要因素的選擇和建立本地圍巖參數與松動圈數據庫。

(3)分析2 種松動圈理論計算方法的適用條件,指出強度準則法受限于均質巖體中靜水應力作用下軸對稱圓形巷道模型,而數學模型法受制于影響因素考慮不足與數據庫噪聲等條件。在工程應用中,不主張在難以符合強度準則法的假設和未知的次要因素影響較大的條件下用計算的方法確定松動圈厚度,應強調松動圈現場測試的必要性。

(4)未來的研究應重視巖石軟化方法,關注深部巖體、非均質各向異性巖體等多種地質條件下松動圈的理論計算,以及矩形及非規則形狀巷道松動圈的理論計算,并提高預測精度。