一種基于冷鏈低碳物流路徑的混合優化算法

邵可南，呂成瑤，張帥帥，宮 婧

(南京郵電大學 理學院，江蘇 南京 210023)

0 引 言

隨著人們生活水平的提高，越來越多的人選擇在線上購買生鮮商品。近幾年，國內冷鏈物流運輸市場逐步擴大，如何控制運輸成本成為研究的熱點。冷鏈物流是一種新型的物流運輸方式，與傳統物流運輸有較大的不同。首先，冷鏈物流運輸的車輛需要使用額外的電能對生鮮商品進行低溫冷凍；其次，生鮮商品必須要長期保存在低溫環境下，在運輸過程中和卸貨配送過程中的溫度變化都會導致生鮮商品的變質腐敗；再次，冷鏈運輸對于配送時間窗的要求很高，物流運輸車如果在客戶期望的時間窗外到達客戶點，無論是早到和遲到都會付出一定的代價；最后，冷鏈物流過程中使用了降溫裝置，造成的碳排放也會隨之增大，要通過合理規劃路徑減少碳排放。

車輛路徑優化問題(VRP)是一類經典的組合優化問題，這類問題的研究工作有著非常重要的理論意義和應用價值。其中，帶有容量約束的車輛路徑優化問題(CVRP)具有更高的現實意義，所以得到了學術界更加廣泛的關注。目前，國內外學者基于CVRP模型，構建了很多冷鏈物流路徑優化模型。Mansoureh Naderipour等[1]提出了考慮二氧化碳和氮氧化物排放以及開放時間窗的車輛路徑優化模型。趙志學等[2]提出了考慮交通擁堵的冷鏈物流城市配送的綠色車輛路徑優化模型。Ferani E.Zulvia等[3]提出了考慮運營成本、貨損成本、碳排放量、客戶滿意度和時間窗的路徑優化模型。劉虹等[4]提出了考慮客戶厭惡度和總成本的冷鏈物流路徑優化模型。徐松梅[5]提出了考慮了固定成本、運輸成本、制冷成本的帶時間窗路徑優化模型。孫明明等[6]提出了考慮冷鏈物流配送過程中的時間成本、溫度成本和貨損成本的路徑優化模型。

針對CVRP問題的求解算法，可以大致分為兩類，即精確算法和智能優化算法。CVRP是一類典型的NP問題，精確算法雖然可以得到全局最優解，但是隨著問題規模的擴大，算法帶來的運算量會以指數級的速度增長，這是人們無法接受的。因此，絕大多數研究者都將關注點放在了智能優化算法上。20世紀70年代以來，伴隨著仿生學和人工智能科學的發展，人們提出了一系列傳統的智能優化算法，包括粒子群算法、禁忌搜索、模擬退火算法、蟻群算法、遺傳算法以及人工神經網絡技術等。隨后，研究者們也提出了很多改進的智能優化算法。蔣麗等[7]提出了求解眾包配送路徑問題的改進蟻群算法。顏騰威[8]提出了求解VRP問題的改進和聲算法。Ziauddin Ursani 等[9]提出了求解帶時間窗VRP問題的局部遺傳算法。Jean-Fran?ois Cordeau等[10]提出了求解VRP問題的并行迭代禁忌搜索算法。Artur Pessoa等[11]提出了求解異構車隊VRP問題的改進分支定價算法。龐凌[12]提出了結合煙花算法和遺傳算法來求解異質車隊VRP問題。李小川等[13]提出了求解多目標帶時間窗VRP問題的文化狼群算法。殷亞等[14]提出了多種混合蝙蝠算法用以求解帶硬時間窗的多目標車輛路徑問題。

該文提出的冷鏈低碳物流路徑優化模型是一個考慮綜合運輸代價、帶有硬時間窗和容量約束的車輛路徑優化問題模型(CVRP-TW)，并使用模擬退火—遺傳混合算法進行仿真實驗。

1 冷鏈低碳物流路徑優化模型的構建

1.1 模型簡述

根據冷鏈物流運輸的特點及需求，該文構建了多車輛、帶有硬時間窗約束和容量約束并且考慮綜合運輸代價的冷鏈物流運輸模型(CVRP-TW)。模型的結構如圖1所示。

圖1 模型結構

為了界定研究的問題，提出以下假設：

只有一個物流中心，但有若干臺冷鏈運輸車，所有冷鏈運輸車均為同一型號，運輸商品全部是同一種生鮮商品。物流企業事先已經了解所有配送客戶的準確位置、貨物需求量、期望和接受的時間窗和卸貨配送所需要的時間。冷鏈運輸車的最大載貨量不小于任一客戶的貨物需求量。物流企業有足夠的冷鏈運輸車以確保能夠一次性完成整個運輸配送過程。每個客戶的貨物只能由一臺冷鏈物流車為其配送一次，并且所有客戶的貨物需求量都得到滿足。所有冷鏈運輸車在完成最后一個配送客戶的服務之后需要返回物流中心。冷鏈運輸車到達客戶點的時間必須在客戶可接受的時間窗之內。

基于上述假設，該文研究的問題描述為：在一次完整的物流運輸過程，有一個物流中心，若干臺冷鏈運輸車和若干個客戶參與其中，運輸貨物完全為生鮮商品。在保證配送客戶貨物需求量和可接受時間窗的前提下，合理規劃路徑，找到一個綜合運輸代價最小的配送方案。考慮的綜合運輸代價包括運輸固定代價、車輛運輸代價、制冷代價、貨損代價、時間懲罰代價和碳排放代價。

1.2 模型建立

1.2.1 優化目標

根據問題描述，建立考慮綜合代價的CVRP-TW模型，其中優化目標為：

minC=C1+C2+C3+C4+C5+C6

(1)

其中，C1至C6分別表示運輸固定代價、車輛運輸代價、制冷代價、貨損代價、時間窗代價和碳排放代價。

(1)固定代價C1：

C1=mc1

(2)

其中，c1是每輛車的固定代價。

(2)車輛運輸代價C2：

(3)

其中，c2是車輛行駛單位路程所造成的車輛運輸代價，對所有車輛在運送回路上的距離求和并乘上單位運輸代價即為車輛運輸代價。

(3)制冷代價C3：

(4)

其中，p31為車輛行駛過程中單位時間產生的制冷代價，p32為卸貨配送過程中單位時間產生的制冷代價，對車輛行駛時間和卸貨配送時間分別求和乘上對應的單位制冷代價作為總的制冷代價。

(4)貨損代價C4：

其中，p0為生鮮商品的單價，α為車輛行駛中的商品變質率，β為卸貨配送過程中的商品變質率。一個客戶點的商品，從物流中心出發到客戶點會經歷車輛運輸的時間和之前客戶點的卸貨配送時間，在這段時間商品會產生變質，貨損和時間的關系可以用線性關系刻畫[15]。故對運輸時間和卸貨時間分別求和乘上貨物量和相應的變質率作為各客戶點的貨損，再對所有客戶點的貨損求和并乘上商品單價作為總的貨損代價。

(5)時間懲罰代價C5：

(6)

(7)

(6)碳排放代價C6：

其中，p51為冷鏈運輸車早到單位時間的等待代價，p52為冷鏈運輸車遲到單位時間的遲到代價。ε0為冷鏈運輸車空載時行駛單位距離的油耗，εM為冷鏈運輸車滿載時行駛單位距離的油耗，q(k,i,j)為第k輛車行駛在地點i到地點j之間時的車輛載重量。E2為制冷設備工作單位時間產生的能耗，e為二氧化碳排放系數即單位能耗所排放的二氧化碳質量，p6為排放單位質量二氧化碳所產生的代價。式(8)計算了車輛行駛時發動機工作產生的能耗和制冷設備工作時產生的能耗(其中發動機工作產生的代價和車輛當前載重有關)，再乘上單位能耗產生的二氧化碳和單位碳排放代價作為總的碳排放代價[16]。

1.2.2 約束條件

根據上述問題假設，得到模型的約束條件。每個客戶的貨物需求量不能超過一臺冷鏈運輸車的最大載重量，即：

Qj≤QM,j=1,2,…,n

(9)

每個客戶都被服務并且只能由一臺配送車輛為其服務一次，即：

(10)

所有冷鏈運輸車在完成最后一個配送客戶的服務之后需要返回物流中心，即：

(11)

冷鏈運輸車到達客戶點的時間必須在客戶可接受的時間窗之內，即：

(12)

2 求解CVRP-TW問題的模擬退火-遺傳混合算法

CVRP-TW是一類典型的NP問題，需要使用智能優化算法對問題的解空間進行有效的搜索來尋找最優解。該文將使用一種模擬退火-遺傳混合算法來求解CVRP-TW問題。

2.1 算法流程

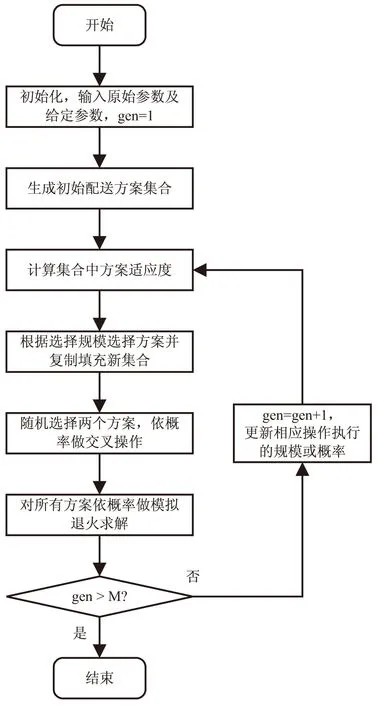
Step1：初始化算法環境，輸入原始參數，設置算法參數：種群規模np，初始選擇規模ns，初始交叉概率pc，初始模擬退火算法執行概率ps，線性參數k1,k2,k3，進化代數M。置迭代數gen=1；

Step3：計算當前種群中個體的適應度，選擇ns+?gen/k1」個體，并復制一部分個體填充新種群；

Step4：對當前種群中所有個體兩兩配對，依概率pc-k2gen進行交叉操作；

Step5：對當前種群中所有個體依概率ps+k3gen執行模擬退火算法；

Step6：gen=gen+1，若gen

2.2 算法實現

由于CVRP-TW問題的特殊性，為考慮算法的計算可行性，該文采用針對該問題的編碼方式和解的更新操作。

(1)編碼方式是自然數編碼，具體方式為在每輛車的配送路徑(即配送客戶點編號序列)后加上0(最后一輛車不用加)。例如：1,2,3,0,4,5,6表示第一輛車配送客戶點編號先后為1,2,3，第二輛車配送客戶點編號先后為4,5,6。算法首先會生成一個配送方案集合。

(2)配送方案選擇操作是選擇ns+?gen/k1」個當前配送方案集合中的方案保留到下一代配送方案。其中最好的前5%配送方案直接保留，剩下的選擇名額會根據適應度用輪盤賭選出，適應度為配送方案代價的倒數。最后對新集合最終適應度排名靠前的np-ns-?gen/k1」個配送方案進行復制填充入新集合。

(3)交叉操作是隨機選擇兩個配送方案，再隨機選擇兩個交叉點，互換選中的兩個配送方案里兩個交叉點之間的編碼(0的位置不動)，再根據交換表更新非交換部分的編碼。

隨著高等教育體制改革的逐步深入，高校辦學規模不斷擴大，師生數量、資產購置、基建投資規模和經費總量都大幅度增長，高校在經費使用、基建工程、物資設備采購等方面擁有越來越多的自主權。因此，廉潔風險防控機制是高校規范權力運行、科學有序發展的必然要求，是完善大學治理體系、建設現代大學制度的現實需要，是加強高校干部隊伍作風建設、推動學校預防腐敗工作的有力抓手[1]。高校要圍繞“人、財、物”等管理監督重點，加強廉潔風險防控機制建設。

(4)模擬退火算法中的配送方案的更新為隨機選擇的兩點交換或三點輪換(0的位置可以改變，但0不能連續或在頭尾)。

為保證配送方案的有效性，只要對配送方案本身進行改變，就要對新配送方案進行約束條件檢測，確保配送方案集合里所有的配送方案都是可行的。SA-GA算法的實現流程如圖2所示。

圖2 SA-GA算法執行流程

2.3 算法小結

模擬退火-遺傳混合算法(SA-GA)是通過對經典的遺傳算法和模擬退火算法進行結合和優化形成的一種混合算法。經典遺傳算法中的變異操作是保證遺傳算法局部搜索精度的操作，該文將這個操作用模擬退火算法進行替換。此外，種群選擇的規模、個體交叉的概率和對種群每個個體執行模擬退火的概率采用動態設置，以保證在算法執行初期能有較大的全局搜索范圍，在算法執行中后期能夠對相對固定的種群進行較大次數的迭代尋優，從而在搜索范圍和求解精度兩個方面盡可能保證算法的性能。

3 仿真實驗設計與分析

通過仿真實驗測試遺傳算法的求解效果。問題參數設置如下：一個物流中心要向20個客戶點提供冷鏈物流配送服務，共有四輛冷鏈運輸車，冷鏈運輸車行駛速度為50 km/h、最大載重量12 t，模型的參數如表1所示。

表1 仿真實驗參數設置

續表1

3.1 仿真實驗求解結果

使用上述設定數據進行模擬退火-遺傳混合算法的實驗仿真。設置算法參數如下：最大進化代數M=100，種群規模np=100，初始交叉率pc=0.8，初始模擬退火算法執行率ps=0.8，線性參數k1=3,k2=0.008,k3=0.002，模擬退火算法初始溫度T0=126，終止溫度Tf=91.7，降溫系數αc=0.968 8，Markov鏈長度Lk=1。隨機生成初代配送方案集合，執行20次模擬退火-遺傳混合算法，得到最優代價為5 901.5，最佳配送方案中四輛冷鏈運輸車的配送代價分別為1 453.6、1 509.7、1 417.0和1 521.2。在求解算法中每一次更新解都會進行約束條件檢驗，所以最優解是有效的。

3.2 實驗結果與分析

為了驗證算法的有效性，該文使用經典的遺傳算法和模擬退火算法各進行20次實驗仿真，三種算法的求解效果如表2所示，求解最優解時的收斂軌跡如圖3所示。

表2 仿真實驗結果比較

圖3 收斂軌跡

根據表2所示，模擬退火-遺傳混合算法相比前兩種經典算法有著更好的求解性能，這主要體現在：

(1)求解效率提高。

模擬退火-遺傳混合算法在相同次數的實驗下比兩種經典算法有著更小的平均收斂代數，意味著混合算法的搜索效率更好。從最優解的離散情況來看，混合算法的最小代價標準差介于兩種算法之間。

(2)搜索范圍較大。

模擬退火-遺傳混合算法求出的最優配送方案的綜合代價優于兩種經典算法，這表明了混合算法的搜索范圍是較大的，并且最優解沒有陷入局部最優，收斂到全局最優。

(3)求解精度更高。

模擬退火-遺傳混合算法的平均代價比兩種經典算法要好，表明了混合算法在每個生成解的領域內有著較高的搜索精度。

模擬退火-遺傳混合算法可以看作是模擬退火算法和遺傳算法的一種折中方案。如果智能優化方法既要擴大搜索范圍，又要提高求解精度，勢必要增加運算量。所以模擬退火-遺傳混合算法是旨在保持相同數量級運算量的前提下，對搜索范圍和搜索精度的一種權衡。混合算法在執行的前期盡可能地擴大搜索范圍，避免算法陷入局部最優解，在執行的中后期根據動態概率的設定盡可能使種群穩定下來，讓模擬退火算法對于每個個體有盡可能大的執行次數，提高個體領域內的搜索精度，并且由于每個個體領域的搜索是獨立的，也可以保證算法在中后期的搜索范圍。上述實驗結果也表明了模擬退火-遺傳混合算法相對于前兩種經典算法而言，是一種更加高效的智能搜索方法。同時，模擬退火-遺傳混合算法實現簡單，繼承了遺傳算法的魯棒性和潛在的并行性，有著較高的實用價值。

4 結束語

根據當前冷鏈物流運輸行業的需求，建立了帶硬時間窗的冷鏈低碳物流路徑優化模型，確定了以綜合代價最優為目標的CVRP-TW問題。其后通過遺傳算法和模擬退火算法這兩個經典的智能優化算法對建立的模型進行仿真實驗求解。之后根據遺傳算法和模擬退火算法的優缺點，將兩種經典算法進行改進和結合，提出了模擬退火-遺傳混合算法。通過仿真實驗模擬求解，驗證了模擬退火-遺傳混合算法在解決冷鏈低碳物流路徑優化問題上有著更好的效率并且能給出更好質量的解。下一步考慮將這一算法應用到多物流中心和多配送車型等更多約束的路徑優化問題的求解上。