基于博弈和網絡流的任務打包定價模型

楊煥煜，邵子朋，高漢成，沙 超，王汝傳

(南京郵電大學 計算機學院、軟件學院、網絡空間安全學院，江蘇 南京 210003)

0 引 言

“拍照賺錢”是當下新穎的一種商業模式，企業借助互聯網等平臺將任務發到“線上勞務市場”，“移動工作者”在平臺上接受任務，完成任務并獲得相應的報酬。然而，如果任務定價不合理，就會出現任務閑置的現象，而導致商品檢查任務的失敗。因此，如何制定一個合理的任務定價，是這種商業模式優先考慮的事情。該文提出了基于博弈和網絡流的任務定價方案，在提高任務完成率的情況下使企業發布任務的成本最小。

1 基于博弈的任務定價模型

為了對“拍照賺錢”平臺的任務合理定價，需要對平臺已結束任務信息進行分析，從而得到平臺任務的定價規律。

平臺任務的定價與任務偏僻程度、周圍的會員密集程度和任務密集程度有關。首先利用k-means聚類方法對任務進行聚類，并得到任務的中心點，計算任務距離中心點的距離作為任務的偏僻程度。然后利用最小二乘法擬合平臺的任務定價公式M(p,c,t)，其中p為任務的偏僻程度，c為任務周圍會員的密集程度，t為任務所在地任務的密集程度。

通過上述步驟可以得到平臺發布任務的定價規律，但這些任務的定價并不是十分合理，如沒有考慮會員信譽度因素的影響。為了彌補傳統定價方案的缺陷，提高任務的完成率，對未完成的任務進行價格調整。

平臺與會員之間的交易是一種不完全信息靜態博弈，平臺和會員都是決策者，每個決策者都有自己的決策變量和目標，決策者的行為相互影響，與之相對應的均衡概念為貝葉斯-納什均衡[1-7]。

1.1 模型建立

假定對于每一個任務，平臺的定價為Ms(vs)，即平臺認為任務的價值vs時，平臺給出的定價為Ms(vs)；會員的定價為Mc(vc)，即會員認為任務的價值為vc時，會員給出的定價為Mc(vc)。則vs為平臺接受的最高價格，vc為會員接受的最低價格。

首先，對所建立模型做以下五條假設：

①商家知道任務對自己的真實價值vs，也就是可以支付的最高價值；會員知道任務對自己的真實價值vc，也就是自己做一單任務能接受的最低價格。

②商家不知道任務對會員的真實價值，但知道其概率分布；會員不知道任務對商家的真實價值，但也知道其概率分布。

③由k-means聚類方法得到平臺發布任務的定價規律，而會員也有先驗經驗，對每個任務的定價有自己的估計。需要讓商家的出價和會員的期望定價在相同的區間范圍內浮動。這個區間只要長度范圍一定，就可以任意設定，只要乘上某個參數就可以得到需要的真實值。故不妨假設vs和vc都服從[0,1]上的均勻分布。

④對一組任意給定的vs和vc，如果會員以價格m接單完成任務，則商家比預期任務定價節省m-vs，會員比預期多賺m-vc；如果不成交，雙方效用都為0。平臺和會員都希望自己的利潤最大化，最優定價應該在vs和vc之間。

⑤以上信息為雙方所共有。

P{Ms(vs)≥Mc}

(1)

其中，E[]表示在條件Ms(vs)≥Mc下Ms(vs)的期望，P{}表示事件的概率。

P{Ms≥Mc(vc)}

(2)

如果價格組合(Mc(vc),Ms(vs))同時滿足(1)、(2)，即構成一個均衡。

1.2 線性價格均衡

博弈問題存在許多均衡，該文采用線性價格均衡法。

假設會員和APP平臺的報價分別是任務對二者價值的線性函數，表示為：

Mc(vc)=ac+cc·vc

(3)

Ms(vs)=as+cs·vs

(4)

確定系數ac、cc、as、cs(假設均為正數)，使二者價格組合(Mc(vc),Ms(vs))同時滿足(1)、(2)。

(5)

這是一個二次函數的優化，其最優解為：

(6)

類似地，假設平臺的戰略為(4)，則對于給定的vc，當Mc∈[as,as+cs]時，由式(1)可得會員的最優反應為：

(7)

(8)

(9)

當且僅當Ms(vs)≥Mc(vc)時交易實際上才能發生，將式(8)、式(9)代入得到交易條件為：

(10)

交易效率為能夠實際發生的交易的期望價值與有利的全部交易的期望價值的比值，可求得此時任務完成的概率為[8]：

(11)

1.3 任務重新定價

尋找平臺所有任務中的最高定價Mmax，設滿足任務完成率為α的最小定價為Ms。由式(9)可得平臺最小定價為：

(12)

聯合式(10)、式(12)可得滿足任務完成率為α的最小定價Ms和會員勞動力價值vc。

設任務調整的價格為f，調整未完成任務的定價，使調整后任務定價需大于Ms，即：

f=max(Mi-Ms),i=1,2,…,R

(13)

其中，R為任務總數，Mi為平臺對每個任務的定價。

綜上所述，任務經過調整后的定價模型為：

(14)

2 基于網絡流的任務打包模型

在實際情況下，多個任務可能因為位置比較集中，導致用戶會爭相選擇，將任務聯合打包發布可以提高任務完成率，同時降低APP平臺的花費。針對該問題建立網絡流模型[9-14]，并建立目標函數以得到最佳任務打包方案。

2.1 網絡流模型建立

構造加權有向圖G={V,E}，如圖1所示。網絡分為四層，分別為源點S、任務點Ci(i=1,2,…,R)、會員點Di(i=1,2,…,R)、匯點T，其中R為任務總數，H為會員總數。對于圖中的每一條邊e∈E均帶有三個權值：容量capacity(e)、流量flow(e)和費用cost(e)。在S與所有的Ci之間添加有向邊，這些邊的容量為1，流量為1，花費為0。

圖1 網絡流模型結構示意圖

根據會員預定任務開始時間和信譽度確定會員優先級，預定任務時間越早且信譽度越高優先級越大，APP平臺按照會員優先級從高到低給會員分配任務。首先對每個會員i，以會員為圓心尋找半徑為d1圓的區域內的所有任務，然后在這些任務中不斷搜尋距離最小的兩個任務，若找到兩個任務m、n間距離小于d2，則將這兩個任務打包，并在網絡中添加有向邊、，且容量、capacity()=1，流量、flow()=1。由于兩任務相距很近，會員完成任務方便，可以將二者的價格以一定比例降低，二者距離越近，降價越多，即：

(15)

(16)

其中，α為降價系數[15]。

剩余未打包的任務，對所有剩余任務k，若任務在已結束項目中為完成狀態，則在網絡中加入有向邊,且容量capacity=1，流量flow=1，cost=Mk；若任務在已結束項目中未完成，則可認為此任務不會被該會員完成，此時在網絡中加入有向邊,且容量capacity()=1，流量flow()=0，cost()=0。

最后在所有Di與T之間添加有向邊，對于會員i，容量為該會員的預定任務限額，即：

capacity()=li

(17)

流量為該會員完成的任務總數，即：

(18)

花費為該會員完成任務的花費總和，即：

(19)

至此，網絡流模型建立完成。

2.2 目標函數確定

以平臺花費最少、任務完成數量最高為目標求解出的打包的方案即為所求的任務打包方案，即目標函數為：

(20)

3 模型求解

該文使用的數據集來源于2017年高教社杯全國大學生數學建模競賽。對任務數據信息進行分析得到平臺任務定價規律，并根據以上建立的基于博弈的任務定價模型和基于網絡流的任務打包模型對任務定價方案進行變更，求解出最佳任務定價、打包方案。

3.1 求解平臺定價規律

首先將所有任務信息、會員信息導入地圖，并在地圖中標注所有任務信息。導入后發現大部分任務是分布在廣東省內的佛山、廣州、東莞、深圳四個城市之中，有若干任務點分布偏離太大作為異常數據不予處理。

會員分布如圖2所示，導入后發現大部分會員是分布在廣東省內的佛山、廣州、東莞、深圳四個城市之中，有若干會員分布偏離太大作為異常數據不予處理。

圖2 會員分布

對任務坐標點進行聚類分析，根據任務的密集程度可將任務分為四類，四類任務的中心點分別位于廣州、東莞、深圳、佛山四個城市，即每類任務都以其中心城市為中心向周圍擴散。用k-means聚類算法畫出任務分布的聚類圖，如圖3所示。

圖3 任務聚類

計算任務距離中心點的距離作為任務的偏僻程度p，任務的偏僻程度越大，任務定價越高。以每個任務為中心，半徑2 km的范圍內會員的數量記為會員的密集程度c，半徑2 km的范圍內任務的數量記為任務的密集程度t，會員、任務密集程度越大，任務定價越低。

利用最小二乘法擬合平臺的任務定價公式M(p,c,t)，分別嘗試擬合一次、二次、三次函數，發現擬合出的二次和三次函數誤差相差不大，因此這里采用二次函數形式，得出平臺的任務定價規律如下：

M=72.203+0.062 7·c2-0.797 7·c+

0.018 9·t2-0.702·t-0.000 091 476·p2+

0.021 6·p

(21)

分析可知當前任務未完成原因主要有：

①任務完成率與任務定價水平有關，標價越高的任務，完成率越高。

②繁華地帶任務未完成率遠大于外圍地區。這可能是因為市中心人們生活節奏快、工資高、空閑時間少，任務定價沒有足夠的吸引力等。而外圍地區恰好相反。

③與地區收入水平有關，比如深圳會員數量多、交通好，但定價相對太低，對人群沒有足夠的吸引力。

④地理位置：地理位置的差異會影響到任務的完成。當地形復雜時，任務也就變得更加困難，導致任務的無法完成。

⑤人口密度：在人口密度小的地方，會有很多任務未完成。

⑥突發狀況：實際生活中，人們總會遇到各種事情，心情不好、堵車、假期、店家拒訪等。這些突發狀況使任務完成的可能性降低。且天氣惡劣時，人們的參與意愿會降低，可能會由很多任務未完成。

3.2 基于博弈的任務定價模型求解

計算佛山、廣州、東莞、深圳四個區域已結束任務的完成率分別為67.4%、54.7%、95.3%、36.2%。由于東莞任務完成率以達到95.3%這一較高水準，因此不再對以東莞為中心的區域內的任務進行定價調整。利用上述任務定價模型分別對佛山、廣州、深圳三個區域內的任務進行重新定價。求解出佛山、廣州、深圳三個區域的會員勞動力價值、最小定價、價格調整大小，如表1所示。

表1 會員勞動力價值、最小定價和價格調整大小

新定價方案與原定價方案進行比較，原定價方案中平臺需支付總花費為57 707.5，調整定價后平臺總支付花費為60 011.5，平臺每件任務平均花費上漲3.9%，任務完成率整體提高到95%，即總任務完成率提高了31.6%。

與應用基于博弈論的任務定價模型之前的任務完成情況對比可知，平臺增加的花費相比于任務完成率的上漲程度可以說微不足道，平臺在微小的損失下大幅度提高了任務完成率，體現了任務定價模型的普適性與最優性。可以說，通過價格博弈模型的定價方案，最大化了APP平臺和會員的利潤。

3.3 基于網絡流的任務打包模型求解

基于任務、會員地理位置信息，設置合適的搜索半徑；根據市場規律，設置降價系數α=0.5。對上述網絡流模型進行求解，求解出共有152個任務被打包為76組任務包，部分打包結果如表2所示。

表2 部分打包結果

計算打包后平臺所需支付總花費為57 416元，相比于第一步修改定價后平臺總花費下降了2 595元。同時總任務完成率為95.45%。

通過基于網絡流的任務打包模型，在降低平臺花費的同時任務完成率仍略有提高，進一步提高了APP平臺和會員的利潤，充分證明了模型的有效性和正確性。

4 靈敏度分析

針對任務打包模型，為了進一步檢驗采用的搜索半徑、降價系數的合理性，該文對搜索半徑和降價系數分別進行了靈敏度分析。

4.1 搜索半徑靈敏度分析

根據任務和會員的密集程度，該文以0.1為步長，在搜索半徑范圍內計算任務打包結果、任務完成率及平臺的總花費數額，計算結果如表3所示。

表3 搜索半徑靈敏度分析

續表3

為了更加清楚地顯示搜索半徑對任務打包結果的影響，根據以上結果作散點圖，如圖4、圖5所示。

圖4 搜索半徑對平臺花費的影響

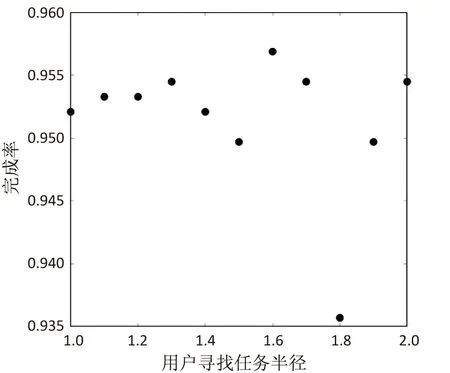
圖5 搜索半徑對任務完成率的影響

由圖4、圖5可知，在范圍內任務的完成率和平臺的花費金額均呈波動狀態。在文中取值時，APP平臺的花費最低且任務完成率相對較高，此時APP平臺和會員雙方得到的利益最大。

4.2 降價系數靈敏度分析

為了增加可信度與真實性，該文對降價系數進行靈敏度分析。以0.1為步長，在范圍內計算平臺的總花費數額，繪制降價系數對APP平臺花費的結果，如圖6所示。

圖6 降價系數對平臺花費的影響

由圖6可知，APP平臺的花費會隨著降價系數的增加而減少。但是根據任務未完成原因的分析，任務完成率與任務定價水平有著密切的關系，在實際生活中標價越高的任務，完成率越高，當標價過低時任務對用戶的吸引力也會有所降低，因此采取較為折中的降價系數α=0.5。

5 優勢與創新點

該文提出的定價規律模型的建立更多基于理性分析和合理推導，結合實際情況對任務完成情況給出解釋。利用多元回歸方程刻畫任務定價的各項細節，將任務定價問題一般化，從而避免了當數據發生變動時，定價原則隨之變動的問題。

考慮到商家與會員之間的價格博弈的關系，切合實際，利用博弈論很好地模擬出任務的完成率，并且保證了商家收益盡可能大。

建立任務打包模型，從網絡流中最小費用最大流的視角看待整個問題，在最大化任務完成率的同時將公司所需費用考慮在內。打包原則貼合實際容易被人們接受。

在數據處理方面，針對所給數據進行詳細分析，得到任務執行的具體情況，在進一步進行劃分后，得到的數據具有比較明顯的地域特征，為制定定價方案提供了數據資料。

6 結束語

提出了基于博弈和網絡流的任務打包定價模型，即在已結束的任務信息基礎上，首先引入貝葉斯-納什均衡理論重新建立任務定價方案，然后再基于最小費用最大流思想建立網絡流模型將部分任務聯合打包發布，在保障任務的完成率的前提下使企業付出酬金最小。在所用示例中，重新定價后，平臺任務完成率提高至95.45%。

但是在引用博弈論時將每個城市的所有會員的理想價格定為統一的價格，沒有考慮各個會員之間的經濟、社會地位等因素會對理想價格的影響，從而使理想價格與個別會員存在一定偏差。

“拍照賺錢”這種移動互聯網下的一種自助式服務模式正隨著移動互聯的發展不斷在人們的日常生活中普及。該文基于移動互聯網下“拍照賺錢”的任務定價與打包模型有著重要的現實意義，對于任務接受者來說，完成多個任務所需的時間更少，獲得的報酬更高，獲取適合自己的任務信息更加方便。對于“拍照賺錢”軟件來說，增加了任務完成率，能夠吸引更多人使用該任務平臺，增加了軟件平臺的收入。該文采用多元非線性回歸方法以及基于網絡流的最小費用最大流算法所建立的任務定價與打包模型在日常生活中的諸多問題中也有著廣泛應用，對其他定價、規劃問題也有一定的指導作用。