基于同步提取變換的滾動軸承微弱特征增強與提取方法

胡志峰，李志農，，朱 彤，王成軍

(1.南昌航空大學 無損檢測技術教育部重點實驗室， 南昌 330063 2.安徽理工大學 礦山智能裝備與技術安徽省重點實驗室， 安徽 淮南 232001)

軸承是旋轉機械中應用最廣泛的零部件之一，在旋轉機械中，軸承發生局部故障時，其故障特征常隱含在含噪的振動信號中，因此對振動信號進行故障特征提取，特別是早期微弱故障特征的提取，對滾動軸承的故障診斷具有顯著意義[1]。而時頻分析技術可以將信號的時域特征和頻域特征有效結合起來，更好的分析信號的局部特征[2]，經典的線性時頻分析方法如短時傅里葉變換，小波變換，S變換[3-4]，廣義S變換[5-6]等，由于受到Heisenberg 不確定性原理的制約，所得時頻譜能量發散嚴重，難以同時獲取高精度的時間分辨率和頻率分辨率[7]。雙線性時頻分析，如魏格納-威爾變換(Wigner-Ville distribution，WVD)及其衍生方法[8-9]，該類處理方法具有高時頻分辨率，但存在交叉項，且其時頻譜不易解釋。而結合經驗模態分解[10]的時頻分析方法，如 Hilbert-Huang變換[11]，變分模態分解[12-13]，經驗小波變換[14-15]等，具有較高的時頻分辨率，但此類方法至今未能建立堅實的數學基礎，不可避免的存在端點效應、模態混疊等問題，在分解復雜信號的準確性存在較大影響，甚至其分解結果存在不確定性，故上述傳統的時頻分析方法由于自身固有缺陷不能夠較好的分析滾動軸承的微弱故障特征。近年來，為了獲取更高的時頻分辨率，許多研究人員將時頻重排方法引入到傳統的時頻分析中，時頻重排方法本質是在傳統時頻分析的基礎上對能量進行二次重排，以改善時頻譜的能量聚集性。Auger等[16]基于傳統時頻分析方法提出了一種后處理重排算法，利用時頻相位信息，通過重排算子將發散的時頻能量重排到時頻脊線上，從而獲取高分辨的時頻譜，但不能支持對信號的重構。Daubechies等[17]提出一種同步擠壓變換的方法，僅考慮頻率系數上的重排，犧牲一部分能量聚集性，但保證了多分量信號的拆解和重構性能。

近期，于剛在同步擠壓變換算法的影響下，以理想時頻分析為目標，旨在擺脫海森堡不確定性原理的限制，提出了一種新穎的時頻分析方法—同步提取變換(Synchroextracting transform，SET)[18]，該方法基于短時傅里葉變換，構建出同步提取算子，提取出短時傅里葉變換時頻譜中時頻脊線位置處的時頻系數，從而顯著提高時頻分析精度，該方法有效克服了傳統時頻分析方法能量發散、特征模糊的問題，此外，該方法計算復雜度低，運算速度快，因此易于微弱信號特征提取與增強。基于同步提取變換的獨特優勢，本文將同步提取變換引入到滾動軸承微弱故障信號的特征提取中，進行仿真研究，同時與傳統的時頻分析方法進行對比，最后，將該方法應用到滾動軸承微弱故障信號的特征提取和增強中，并進行實驗驗證。本文的研究為強背景噪聲下的微弱故障特征提取提供一種新方法，具有一定的理論價值和實踐應用價值。

1 同步提取變換原理

SET是后處理技術，可分為3個步驟：

步驟1：對信號進行短時傅立葉變換(STFT)，將時間信號變成時間-頻率信號；

步驟2：根據相位信息計算出瞬時頻率；

步驟3：提取短時傅立葉變換(STFT)在瞬時頻率位置上的時頻系數。

設待分析信號z(t)=Aeiω0t，待分析信號先經過短時傅立葉變換由一維的時間信號變為二維的時頻信號：

(1)

式中，g(u-t)通常為高斯窗函數。

但在時頻域內，由于短時傅里葉的窗口函數是寬寬固定，易導致形成能量模糊的頻譜圖，所以要對短時傅立葉變換公式進行改進，根據帕賽瓦爾定律(Parseval’s theorem)可對(1)式進行改寫：

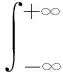
(2)

(3)

使u-t=t′，則有：

(4)

將式(4)代入到式(2)：

(5)

在式(5)結果上增加一個頻移算子e-iωt：

(6)

則有：

(7)

待分析信號的傅里葉變換可表示為：

(8)

則將式(8)代入到式(7)中，則有：

(9)

為了計算出式(8)的瞬態頻率，則需計算Ge(t，ω)關于時間的偏導：

Ge(t，ω)·i·ω0

(10)

當Ge(t，ω)不為0時，二維的瞬時時頻ω0(t，ω)則表示為：

(11)

由式(8)，可以提取出短時傅里葉變換在瞬時頻率位置上的時頻系數，從而實現高精度的時頻譜，通常適用同步提取算子SEO得到：

Te(t，ω)=Ge(t，ω)·δ(ω-ω0(t，ω))

(12)

其中同步提取算子滿足以下條件：

(13)

從而實現了時頻特征的精確提取。

2 仿真研究

考慮如下強背景噪聲仿真信號：

x(t)=e-tsin(2π(30t+5sin(2t)))+

0.15randn(size(t))

(14)

設置該信號采樣頻率為100 Hz，采樣時間為4 s，圖1為仿真信號x(t)時域圖，圖2是該信號的頻譜圖，由圖2可知，該信號具有多個頻率特征，但不能清晰的顯示出頻率特征隨時間的變化規律，對該仿真信號x(t)分別進行短時傅里葉變換，同步提取變換和同步擠壓短時傅里葉變換，分別得到了該仿真信號的時頻圖及局部放大的時頻圖，如圖3、圖4、圖5所示。對比局部放大的時頻圖，同步提取變換具有較高的時頻精度，且具有一定的抗噪性能，由于噪聲成分的存在，在圖3中，仿真信號特征頻率與噪聲成分發生混疊，時頻信息模糊，在圖5中，雖然同步擠壓短時傅里葉變換在一定程度上提高了時頻精度，但是由于噪聲成份的存在，同步擠壓短時傅里葉變換將部分噪聲成份也“擠壓”至仿真信號時頻脊線上，使得時頻脊線成份復雜，難以區分信號微弱特征，而同步提取變換在一定程度上仍然保持了高精度的時頻信息，具有一定抗噪性能。因此可以實現對實際信號的微弱特征的提取。

圖1 信號x(t)的時域圖

圖2 信號x(t)的頻譜曲線

圖3 (a)信號x(t)的短時傅里葉變換, (b)信號x(t)的短時傅里葉變換的局部圖

圖4 (a) 信號x(t)的同步提取變換, (b)信號x(t)的同步提取變換的局部圖

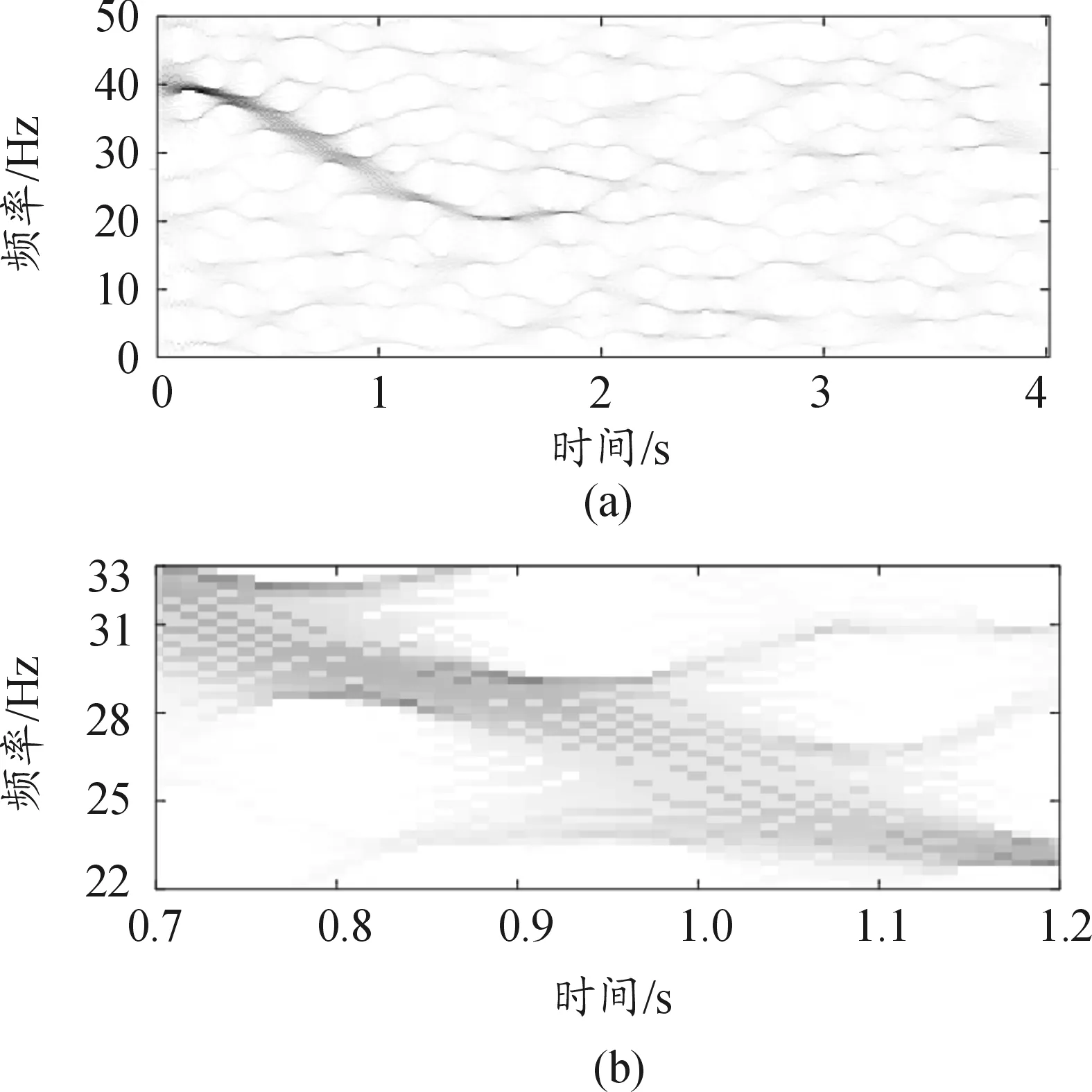
圖5 (a)信號x(t)的同步擠壓變換, (b)信號x(t)的同步擠壓變換的局部圖

3 實驗研究

為進一步驗證該方法的有效性，將SET應用到滾動軸承振動信號的微弱特征提取中，采用美國西儲大學電氣工程實驗室中的軸承試驗數據其軸承實驗和采集裝置如圖6，并考慮添加背景噪聲進行分析。軸承類型為深溝球軸承，采用的軸承規格為：內圈直徑25 mm，外圈直徑52 mm，厚度15 mm，滾動體直徑7.94 mm，節圓直徑39.04 mm。

軸承振動信號由加速度傳感器采集，采樣頻率12 kHz，轉速為1 797 r/min，在軸承外圈用電火花加工直徑為0.177 8 mm的缺陷，用來模擬軸承外圈的輕微損傷。可計算出外圈故障特征頻率為107 Hz。

為更好驗證該方法的可行性，在原信號的基礎上添加了13.3 dB的背景噪聲，由于軸承發生故障時所測得的信號是調制信號，而故障信息往往都包含在低頻的沖激信號中，因此，需要對故障信號進行Hilbert變換解調，軸承故障加噪后信號的時域和解調頻譜如圖7、圖8所示。

圖6 西儲大學軸承實驗和采集裝置

圖7 0.1778 mm缺陷時加噪的軸承外圈的時域圖

圖8 0.1778 mm缺陷時的軸承外圈的頻譜圖

由圖8可知，雖然頻譜圖中可以反映故障信號的特征頻率，然而，無法故障頻率特征隨時間的變化規律，有必要從時頻圖上去揭示。圖9為信號的短時傅里葉變換的時頻圖譜。短時傅里葉變換的時頻圖譜能反映故障的時頻信息，然而，由圖9可知，其結果難以看出故障特征信息的倍頻信號，且與嚙合頻率發生了較為明顯的頻率混疊，圖10為同步擠壓短時傅里葉變換得到的滾動軸承外圈故障時頻分布。由圖10可知，采用同步擠壓短時傅里葉變換，雖然有較高的時頻精度，但是倍頻特征反映不明顯，且將噪聲成份擠壓至信號的時頻成份中。采用本文方法得到的滾動軸承外圈故障時頻分布如圖11所示，由圖11可知，同步提取變換明顯優于短時傅里葉變換和同步擠壓短時傅里葉變換，具有較高的時頻精度，并將信號的倍頻清晰的表征出來。

圖9 軸承外圈信號的短時傅里葉變換的時頻圖譜

圖10 軸承外圈信號的同步擠壓短時傅里葉變換的時頻分布

圖11 軸承外圈信號的同步提取變換的時頻分布

4 結論

將SET方法應用到滾動軸承微弱故障特征提取和增強中，通過仿真分析，驗證了該方法能夠清晰的表征出強背景噪聲環境下的微弱故障信號的時頻特征，比較同步擠壓短時傅里葉變換和短時傅里葉變換兩種方法有非常高的時頻精度，能夠識別軸承輕微損傷的故障特征。該方法為機械微弱故障特征增強與提取提供了一種有效的方法。