LS-DYNA軟件中4種不同爆炸荷載施加方法的比較

周 清，張云海，齊 麟

(1.濱州市規劃設計研究院， 山東 濱州 256600; 2.中國民航大學 機場學院， 天津 300300)

結構抗爆分析通常采用以數值分析為主、試驗為輔的研究方法。通用動力學軟件LS-DYNA被廣泛地應用于抗爆數值分析中，LS-DYNA為用戶提供了4種不同的爆炸荷載施加方法。為研究何種爆炸荷載施加方法最能反映真實的情況，首先選用具有代表性的鋼筋混凝土板(以下簡稱RC板)抗爆試驗文獻作為研究對象，然后利用LS-DYNA軟件建立與試驗文獻完全相同的數值分析模型并采用4種不同的方法施加爆炸荷載，最后通過與文獻的試驗結果進行比較選擇出最合理的爆炸荷載施加方法。

1 LS-DYNA軟件中4種不同的爆炸荷載施加方法

1.1 方法1：將爆炸荷載等效為三角形均布荷載直接施加于受爆面

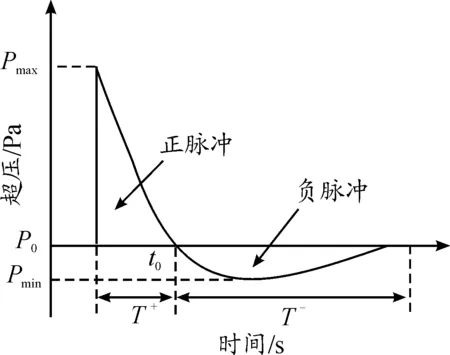
圖1 爆炸波沖擊壓力時程曲線

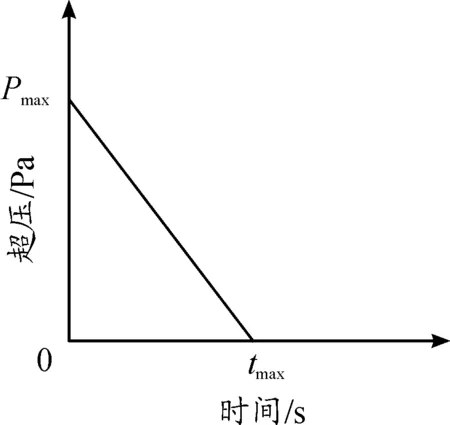
圖2 簡化后的三角形壓力時程曲線

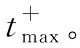
Pmax=1.407 17/Z+0.553 97/Z2-0.035 72/Z3+

0.000 625/Z4(0.05≤Z≤0.30)

(1)

Pmax=0.619 38/Z-0.032 62/Z2+0.213 24/Z3

(0.30≤Z≤1)

(2)

Pmax=0.0662/Z+0.405/Z2+0.3288/Z3

(1≤Z≤10)

其三，以今香日德為中心的道路：從這里通往境外的道路大體有五條④陳良偉：《絲綢之路河南道》，中國社會科學出版社，2002年，第200-205頁。：

(3)

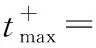
0.033 5Z4)×10-3×W1/3

(4)

1.2 方法2：直接調用LS-DYNA軟件中的爆炸超壓數據

LS-DYNA中存有由試驗得到的TNT空中爆炸超壓數據，可以利用關鍵字按以下方法直接調用。首先采用*LOAD_BLAST_ENHANCED關鍵字定義TNT當量、爆炸點及爆炸類型，考慮地面反射作用時，還應借助關鍵字*DEFINE_VETOR定義地面與爆炸點之間的法向向量；然后采用關鍵字*LOAD_SEGMENT與*LOAD_BLAST_SEGMENT_SET定義爆炸波的接觸面。文獻[4-6]采用該方法施加爆炸荷載。方法2同樣不需要建立空氣與炸藥的數值分析模型，施加方法簡單，計算時間比方法1略長。

1.3 方法3：建立炸藥與空氣數值分析模型并借助其狀態方程施加爆炸荷載

方法3在抗爆數值分析中應用最廣。采用方法3的建模方法時，需要對炸藥和空氣分別單獨劃分網格并賦予其各自的狀態方程，且炸藥網格和空氣網格應在交界面上共節點。文獻[7-10]采用該方法施加爆炸荷載。炸藥需要借助關鍵字*MAT_HIGH_EXPLOSIVE_BURN模型配合Jones-Wilkens-Lee(JWL)狀態方程定義[10]，以炸藥爆轟產物的壓力表示的JWL方程為：

(5)

式(5)中：P1為爆炸壓力；V為相對體積；E0為初始內能密度；A、B、R1、R2、ω為狀態方程參數。JWL方程參數與TNT材料參數取值如表1所示，表中ρ表示炸藥密度，DT表示爆轟速度，Pcj表示爆轟壓力。

空氣采用*MAT_NULL配合*EOS_LINEAR_POLYNOMIAL狀態方程定義[10]，其線性多項式狀態方程為：

P2=C0+C1μ+C2μ2+C3μ3+

(6)

式(6)中：μ=ρ/ρ0-1，ρ表示空氣的當前密度，ρ0是初始時刻的空氣密度；P2為空氣壓力；C0～C6為多項式方程系數；E1為內能密度；V0為初始相對體積。各相關參數取值見表2。

表1 TNT炸藥參數[10]

表2 空氣參數[10]

方法3操作比以上方法1和方法2復雜，并且需要消耗較長的計算時間。

1.4 方法4：初始體積分數法施加爆炸荷載

方法4是在方法3基礎上改進而得到的一種爆炸荷載施加方法，其施加方式詳見文獻[11-13]。該方法首先需要定義炸藥、空氣的材料參數與狀態方程；然后借助關鍵字*ALE_MUTI-MATERIAL_GROUP定義一個包含炸藥與空氣的材料組；最后借助關鍵字*INITIAL_VOLUME_FRACTION_GEOMTRY進行填充。以圖3為例說明方法3與方法4的區別，圖3所建模型為1 m×1 m×1 m的正方體空氣與半徑0.2 m的球形炸藥，當采用方法3建模時需分別單獨建立空氣與炸藥的網格。而采用方法4建模時僅需要建立空氣網格作為背景網格，然后利用關鍵字*INITIAL_VOLUME_FRACTION_GEOMTRY在指定區域將炸藥材料填充至建好的空氣網格中，并且不要求空氣網格和炸藥網格共節點。操作完成后，在炸藥幾何模型所占據的空間中，原網格中的空氣被炸藥材料所替代。關鍵字*INITIAL_VOLUME_FRACTION_GEOMTRY的定義如表3所示，共3行。第1行的4個關鍵字定義初始的空氣材料，其中FMSID表示空氣的PART號；FMIDITYP表示PART類型；BAMMG表示空氣材料在材料組中的編號；NTRACE表示填充采樣點數量，可采用默認值。第2行的3個關鍵字定義炸藥材料，其中CNTTYP表示炸藥的形狀，6為球形；FILLOPT表示填充方式，0表示內部填充；FAMMG表示炸藥材料在材料組中的編號。第3行定義炸藥的位置及體積，其中X0、Y0、Z0表示炸藥球心坐標，R0表示球半徑。

圖3 方法3與方法4示意圖

相對于方法3，方法4的優越性體現在以下2個方面：1) 不需要單獨建立炸藥單元，僅需在K文件中將炸藥進行替換，可以非常方便地定義不同藥量的爆炸荷載。2) 可以定義各種形狀如圓形、方形、柱形等炸藥數值分析模型，避免了不規則炸藥體網格劃分的困難。

表3 關鍵字*INITIAL_VOLUME_FRACTION_GEOMTRY的應用

2 試驗文獻的選擇與4種爆炸荷載施加方法的比較

孫文彬[14]對RC板進行了抗爆試驗研究，筆者選取該文獻作為參考對象。試驗采用的2塊RC板尺寸均為1 300 mm×1 000 mm×120 mm。板設計為單向板，長邊簡支，短邊自由。采用雙層雙向配筋，受力的長邊配筋為10@100，非受力的短邊配筋為10@200。板保護層厚度取值25mm。試驗鋼筋采用HRB500，其屈服強度為560 MPa，極限強度為605 MPa，彈性模量為230 GPa。采用C40混凝土，抗壓強度為48 MPa，彈性模量為48 GPa。試驗在愛丁堡國防科技組織的爆炸倉內進行，爆炸點位于RC板中心正上部0.6 m處，爆炸Ⅰ、爆炸Ⅱ的TNT當量為0.079 kg、2.09 kg。爆炸Ⅰ比例距離Z=1.4 m/kg1/3，為了觀測RC板在彈性階段的動力響應。爆炸Ⅱ比例距離Z=0.47 m/kg1/3，為了觀測RC板在塑性階段的爆炸響應和破壞特征。試驗布置及采用方法3建立的數值分析模型如圖4所示。

圖4 試驗布置及數值分析模型示意圖

結合試驗提供的材料數據，采用LS-DYNA的72#材料模型模擬混凝土[15]。當采用國際單位時，72#模型定義C40強度混凝土材料的主要參數如表4所示。其中，MID為材料標識號；ρ為材料密度；A0為初始抗壓強度，負值；RSIZE為單位轉換數值：m/inches；UCF為單位轉換數值：Pa/PSI；LCRATE為所要調用的曲線號。

表4 C40混凝土參數(72#模型)

采用LS-DYNA的3#模型(*MAT_PLASTIC_KINEMATIC)模擬HRB500鋼筋[15]，鋼筋的主要參數采用表5定義。其中，ρ表示密度；fy為屈服應力；HP為硬化參數；ν為泊松比；E和Etan分別為彈性模型和切線模量；C、P為Cowper-Symonds應變率參數；FS為失效應變。

添加關鍵字*MAT_ADD_EROSION定義混凝土單元的失效，定義最大抗壓強度fc max≤40 MPa與最大抗拉強度ft max≤4 MPa為失效準則，當材料強度大于以上任意數值時，混凝土單元將被刪除。鋼筋采用3#模型自帶的失效準則定義，當鋼筋的失效應變大于0.2時，鋼筋單元將被刪除。炸藥與空氣定義為多物質歐拉幾何實體(EULER)，結構體定義為拉格朗日幾何實體(LAGRANGE)，借助于關鍵字*CONSTRAINED_LAGRANGE_IN_SOILD實現爆炸波與結構體的接觸，接觸類型可采用無侵蝕的罰函數耦合。

表5 HRB500鋼筋參數

2.1 爆炸Ⅰ，4種爆炸荷載施加方法的比較

表6 爆炸I數據匯總

圖5 爆炸I，RC板跨中位移時程曲線

通過對表6與圖5分析可知，爆炸Ⅰ時：1) 方法1得到的數值分析結果與試驗吻合最好，其最大加速度amax、最大位移fmax、最大位移出現時間tmax略大于試驗結果。2) 方法2得到的最大加速度amax、最大位移fmax較試驗結果偏小，而最大位移出現時間tmax與試驗結合相吻合。3) 方法3、方法4得到的各數據均大于試驗結果。由于試驗結果的RC板在爆炸Ⅰ時最大位移fmax僅為1.12 mm，方法3、方法4比試驗結果分別增大0.93 mm、1.53 mm。考慮到試驗產生的誤差，其計算結果仍然是合理的。(4)除方法4產生少量塑性變形以外，其余3種方法的RC板均處于彈性階段，與試驗結果相一致。以上說明，爆炸荷載較小時4種爆炸荷載施加方法均能較為準確地反映RC板在彈性階段的動力響應。

2.2 爆炸Ⅱ，4種爆炸荷載施加方法的比較

爆炸Ⅱ的TNT當量為2.09 kg，爆炸點位于RC板中心正上部0.6 m處，比例距離Z=0.47 m/kg1/3。爆炸Ⅱ的RC板發生明顯的破壞，圖6為RC板頂與底的破壞圖。由相關文獻可知，板跨中表現為明顯的彎曲破壞，支座未出現剪切破壞特征。板頂跨中出現120～150 mm的混凝土壓碎區，板底出現2條寬度6～8 mm的主裂縫。板底形成近似正方形的坑，坑邊長約為550 mm，周長約為2 200 mm，最大深度約為65 mm。板跨中產生不可恢復的永久變形，最大撓度為50 mm。

圖6 爆炸Ⅱ，試驗的RC板破壞圖

圖7 爆炸Ⅱ，4種爆炸荷載施加方法的RC板破壞圖

表7 爆炸Ⅱ深坑數據

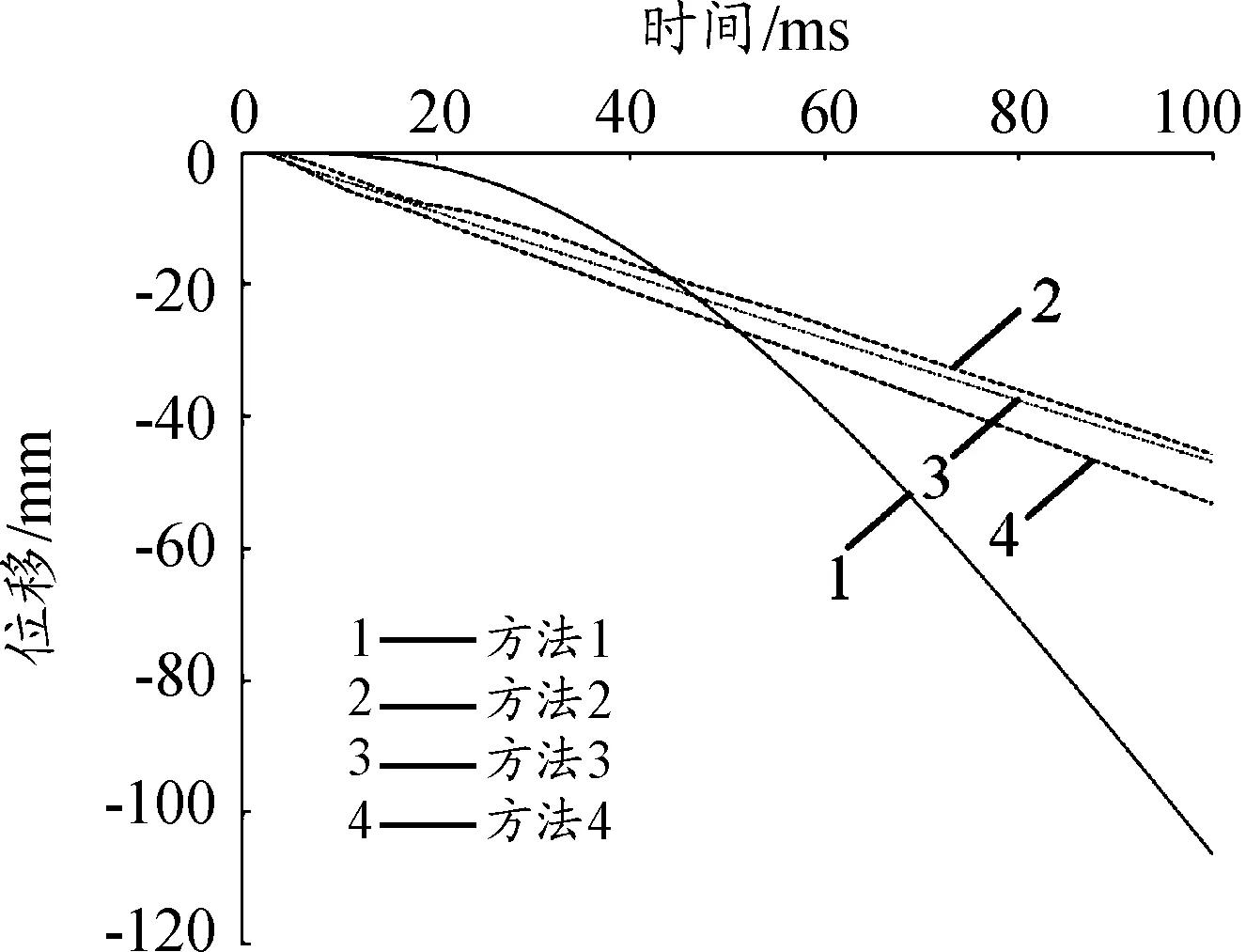
圖8 爆炸Ⅱ，RC板跨中位移時程曲線

3 結論

1) 當爆炸荷載較小時，RC板處于彈性階段，4種方法均能較為準確地模擬結構構件的動力響應。

2)當爆炸荷載較大時，RC板處于塑性與破壞階段。方法3可以較為精確地模擬RC板的破壞特征，方法2與方法4可以近似地模擬板的破壞特征，但與試驗結果存在一定的誤差，不應采用方法1施加爆炸荷載。