LCC-HVDC 系統混合型有源濾波器諧振抑制策略

杜夏冰，趙成勇，吳方劼，史善哲，郭春義

（1. 新能源電力系統國家重點實驗室（華北電力大學），北京市102206；2. 國網經濟技術研究院有限公司，北京市102209；3. 國網河北省電力有限公司，河北省石家莊市050021）

0 引言

目前中國已經運行的特高壓和遠距離超高壓直流工程均為基于電網換相換流器的高壓直流（line commutated converter based high voltage direct current，LCC-HVDC）輸電工程［1］。特高壓直流工程每極均為雙12 脈動換流單元，在運行過程中存在12k±1 次特征諧波，需要裝設大量的無源濾波器組，這些濾波器占地面積很大，跟蹤速度慢，動態調節能力弱，造成甩負荷過程的過電壓等動態特性不能滿足系統運行要求［2］。

混合型有源濾波器（hybrid active power filter，HAPF）作為諧波污染的一種抑制方法，以其優越的濾波性能得到了廣泛的關注［3］。在目前的研究中，有源濾波器（active power filter，APF）拓撲通常為三電平的結構［4-6］，但受到器件耐壓及容量限制，難以滿足LCC-HVDC 系統的諧波補償需求。文獻［7］中，APF 采用級聯H 橋型拓撲結構，通過子模塊串聯實現了容量的自由擴展，可以有效解決這一問題。

但是，從交流側看，APF 可以被認為是一個有復雜內阻特性的電壓源，且換流站母線上還接有無功補償電容器，因此其交流母線耦合點處的阻抗特性復雜，容易產生諧振風險，極大地危害交流系統和直流系統的穩定性［8］。

抑制諧振的方法有很多，如增加系統阻尼［9-10］、改變諧振點［11］、改造阻抗等。文獻［8］通過電容電流反饋的方法來提高系統穩定裕度，相當于等效增強了系統阻尼；文獻［12］通過檢測各個電流計算系統的阻抗分布情況，從而判斷濾波器控制的穩定情況，在此基礎上通過調整指令電流來消除諧振，但是上述2 種方案提高了電流硬件采樣，在實用性上具有一定的限制。文獻［11］通過串聯電感的方法改變諧振點，但模型中未考慮濾波器控制系統中控制延時及其對系統穩定性的影響。事實上，APF 的控制對實時性的要求很高，由于可控器件死區效應的存在以及系統采用數字化控制，控制延時不可忽略［13-14］。且現有的諧振抑制策略受系統參數影響大，在系統參數發生變化時，諧振抑制策略效果將會變差甚至失去作用。

文獻［15］提出了適用于LCC-HVDC 的HAPF拓撲結構及其電流控制策略，并簡要分析了控制延時對系統的影響，并未消除較大延時可能造成的諧振。本文在此基礎上，改善了HAPF 無源部分的拓撲結構，且系統中考慮了換流母線處的無功補償設備，兩者相結合既可以有效改善濾波性能，又可以用已有的無功補償設備來降低HAPF 的容量，實現濾波和無功混合補償，具有良好的經濟效益［16-17］。同時，分析了不同控制延時的系統含電容的情況下，HAPF 的阻抗特性及其對系統穩定性的影響，并提出基于最小均方（least mean square，LMS）算法的自適應諧振抑制策略，通過預測波形，等效補償控制系統中的計算和采樣延時，不僅可以改善HAPF 的阻抗特性，而且能自適應調整預測矩陣，使其可應用于工況以及電路參數變化的情況。最后，在PSCAD/EMTDC 上進行仿真分析及驗證。

1 HAPF 拓撲結構及控制方法

1.1 HAPF 拓撲結構

HAPF 由調諧次數為12 次和24 次的無源部分以及基于H 橋結構的有源部分組成，該結構適用于LCC-HVDC 系統［15］。文獻［15］中，無源部分采用2 組單調諧并聯的結構，而實際LCC-HVDC 工程中大多采用雙調諧濾波器，因此，本文無源部分參照實際工程設置，如圖1 所示，其中：uS、iS和ZS分別表示交流系統的電壓、電流和阻抗。

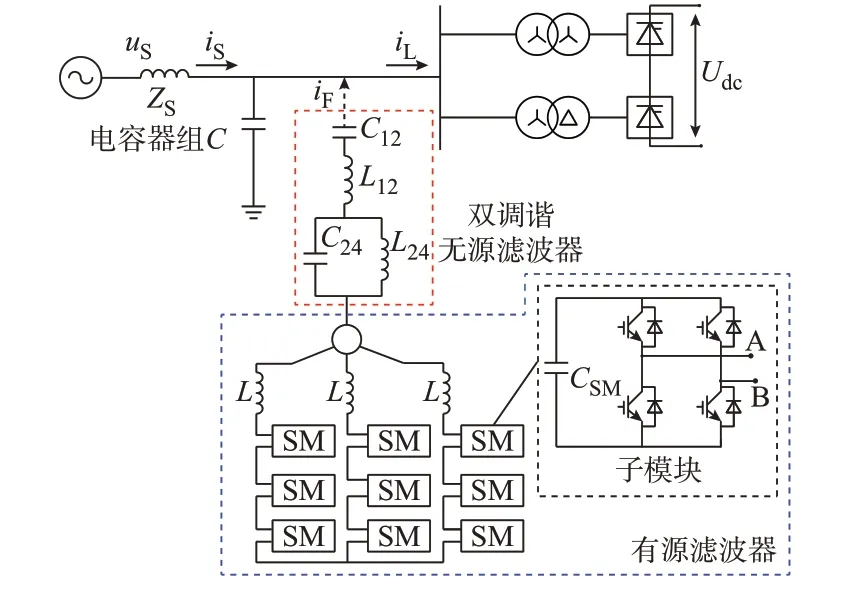
圖1 LCC-HVDC 整流側及級聯H 橋HAPF 拓撲Fig.1 Topologies of rectifier side of LCC-HVDC and cascaded H-bridge HAPF

雙調諧無源濾波器具有一定的調諧帶寬，可以給11 次、13 次、23 次、25 次 諧 波 提 供 低 阻 抗 支 路。同時，控制APF 出口電壓，使基波電壓基本作用于無源濾波器，從而降低APF 級聯的模塊數和造價。通過控制絕緣柵雙極型晶體管（insulated gate bipolar transistor，IGBT）器件的通斷，使APF 輸出一個與負載電流iL的諧波分量相等的補償電流iF來補償諧波部分，如圖1 中虛線箭頭所示。系統無功補償由無源濾波器和無功補償電容器組C 共同完成。

1.2 HAPF 控制方法

根據圖1 中LCC-HVDC 系統整流側及HAPF結構圖，作出其等效電路圖，如附錄A 圖A1 所示。由于平波電抗器的存在，當交流電壓波動時，交流電流基本不變，LCC 在諧波下等同為諧波電流源，APF 等同為一個含內阻的電壓源。圖A1 中：uPCC為換流母線電壓；ZLC為APF 連接電抗L 和雙調諧無源濾波器的等效阻抗；ZC為并聯電容器組的阻抗；ZF為APF 的內阻；uF為APF 的出口電壓。

為降低APF 容量和造價，APF 的容量只用來進行諧波補償以及部分無功補償［15］，從而使絕大部分的電網電壓自動作用于HAPF 無源部分，即

假定電流iFn可以完全補償負載諧波電流iLn，則APF 的出口電壓由補償電流和無源濾波器阻抗決定，即

電流控制采用準比例-諧振（quasi-proportionalresonant，QPR）控制，單個控制器可使補償電流快速跟蹤某一諧波電流，且可應對電網頻率波動的情況［15］。針對LCC-HVDC 系統存在多個特征次諧波的情況，可采用多個并聯的控制器來實現高達37 次的特征次諧波電流控制［18］。

2 HAPF 阻抗模型及諧振機理分析

2.1 考慮控制延時的HAPF 阻抗模型

令HAPF 檢測電流為負載電流，經過高通濾波器可獲取諧波分量iLn，由于可控器件的死區效應和數字化控制給HAPF 的控制過程引入了一定的延時，因此，設置固有延時GT（s），則HAPF 控制框圖如圖2 所示。

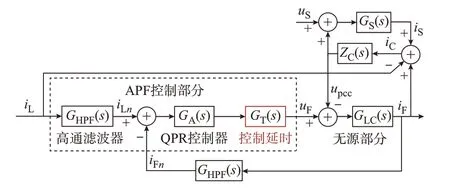
圖2 考慮控制延時的HAPF 控制框圖Fig.2 Block diagram of HAPF control considering control delay

根據控制框圖建立HAPF 的頻域模型：

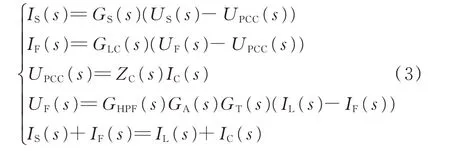
式 中：GS(s)為 交 流 系 統 導 納；GA(s)、GHPF(s)和GLC(s)分別代表QPR 控制器、高通濾波器［19］和雙調諧濾波器。

由此，可得HAPF 等效阻抗ZHAPF（s）為：

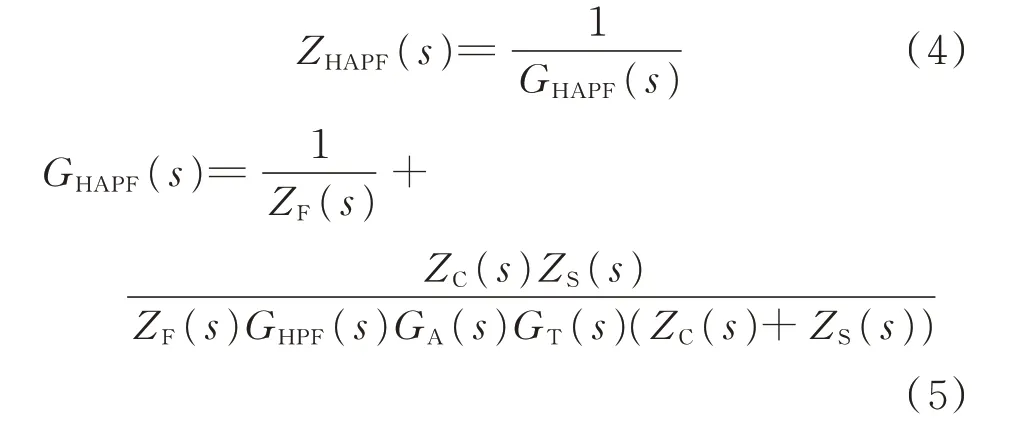
根據附錄B 表B1 給出的參數，繪制頻率特性曲線，如圖3 所示。

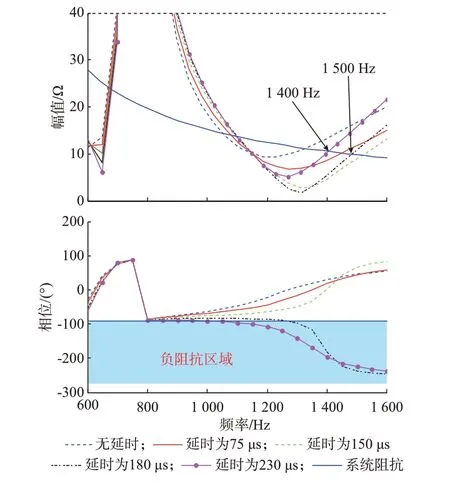
圖3 HAPF 阻抗及電網阻抗的頻率特性曲線Fig.3 Frequency characteristic curves of HAPF impedance and power grid impedance

目前的逆變器采樣頻率通常在6.4～20 kHz 之間，對應的實際控制延時約為1.5 倍采樣周期［20］，即75 μs 至230 μs。由圖3 幅頻特性可知，HAPF 阻抗與電網阻抗在高頻處存在幅值交點，隨著控制延時的增大，交點發生向右50～100 Hz 的偏移，對應相頻特性中，當延時大于180 μs 時，HAPF 在高頻處出現負阻抗特性。綜上，當控制延時大于180 μs 時，系統可能存在28～30 次的高頻諧振風險［21］。

2.2 諧振機理分析

為 驗 證 當 控 制 延 時τ>150 μs 時，HAPF 的 負阻抗特性是否真的導致了系統諧振，進一步將附錄A 圖A1 所示電路進行等效變換，采用線性化小信號模型分析系統特性，得到的2 個交互系統等效電路圖如附錄A 圖A2 所示。圖中電網側U′S(s)和Z′S(s)分別為交流系統和無功補償電容的戴維南等效電壓和阻抗。文獻［21］指出，2 個交互系統的穩定條件為阻抗比滿足奈奎斯特穩定判據。

不同控制延時對應阻抗比的奈奎斯特圖如圖4所示。

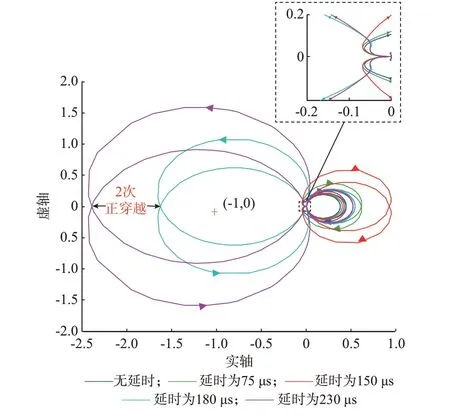
圖4 不同延時下阻抗比奈奎斯特圖Fig.4 Nyquist plot of impedance ratio with different delays

圖4 中，當系統延時τ 不斷增大時，曲線與實軸的交點向左移動，穩定裕度逐漸減小，且當τ 大于180 μs 時，系統不穩定，曲線在負實軸處發生2 次正穿越。因此，當控制延時大于180 μs 時，系統發生諧振，需要進一步設計諧振抑制策略。

3 基于LMS 算法的諧振抑制策略

控制延時導致HAPF 的阻抗特性發生改變，從而使系統存在諧振風險。因此，通過設計一種前饋補償的方法，利用預測下一時刻的波形來消除控制延時帶來的相位滯后，可以為抑制諧振提供思路。

3.1 LMS 算法工作原理

LMS 算法［22］在預測過程中不需要大量歷史數據或數據的統計特性，具有原理簡單、計算復雜度低，可在預測過程中修正濾波參數，使之與實際系統自動匹配等優點。其預測過程如下：

步驟1：獲取當前時刻k 的輸入變量x(k)以及上一時刻x(k-1)的預測值y(k)，計算誤差向量e(k)，如式（6）所示。

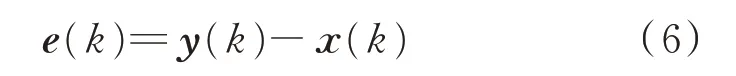
式中：k 為迭代次數。

步驟2：通過式（7）更新預測系數矩陣P(k)。

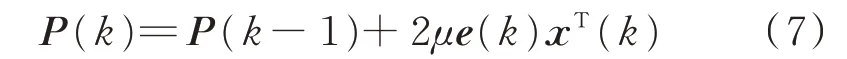
式中：μ 為學習率。

步驟3：利用預測矩陣P(k)和當前的輸入變量x(k)，通過式（8）得到下一時刻x(k+1)的預測值y(k+1)。

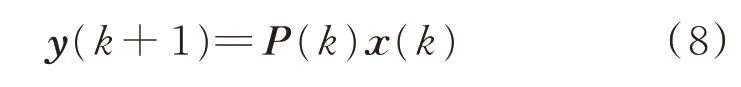
步驟4：重復步驟1、2、3，不斷迭代，最速下降法使得預測誤差趨向極小值。

3.2 自適應諧振抑制策略

3.2.1 諧振抑制策略

已知補償電流iF存在相位滯后，因此在原控制系統的基礎上，引入基于LMS 算法的預測環節，如附錄A 圖A3 所示。選擇補償電流作為預測輸出，使預測后的補償電流的相位超前于原補償電流iF。

為保證預測效果，預測環節選取的輸入量應與輸出量有較強的相關性。由圖1 可知，iF與雙調諧無源濾波器的電容電感參數、APF 出口電壓以及換流母線電壓強相關，狀態變量可選無源濾波器電感電流iL12和iL24、電容電壓uC12和uC24以及無源濾波器兩端電壓差u′F，其中u′F=uPCC-uF；電流iF、iL12、iL24三者并非獨立，取其二作為輸入量即可。因此，輸入、輸出量表示如下：

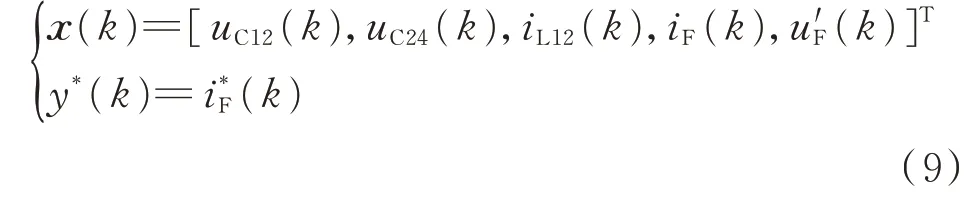
代入LMS 算法，得到：

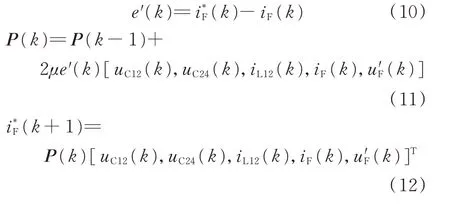
HAPF 預測環節的具體流程如附錄A 圖A4 所示。在每次控制周期中，輸出量通過反饋環節計算APF 的調制信號，改變APF 出口電壓，每次迭代，次數k 增加1 次。由當前時刻的輸出值預測下一周期的輸入值，即預測值構成的電流波形相位超前實際波形一個控制周期。引入LMS 算法后，相當于等效縮短了控制延時，從而改變了HAPF 的阻抗特性，提高了系統穩定性。

3.2.2 初始預測矩陣

要想預測模塊穩定啟動，并且經過迭代后預測系數矩陣能收斂到精確值，需要確定初始預測矩陣P(1)。為此，建立微分方程如下：

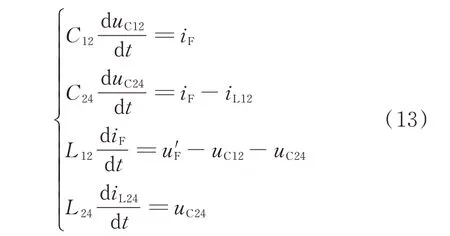
整理得到狀態方程表達式：

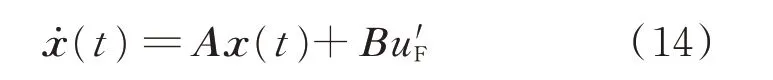
式中：

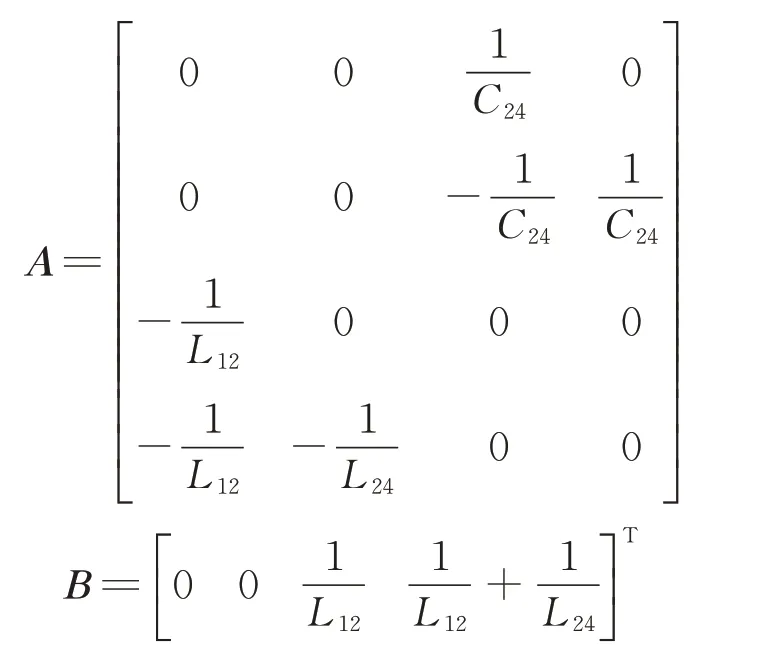
將式（14）所示狀態方程離散處理，得到：

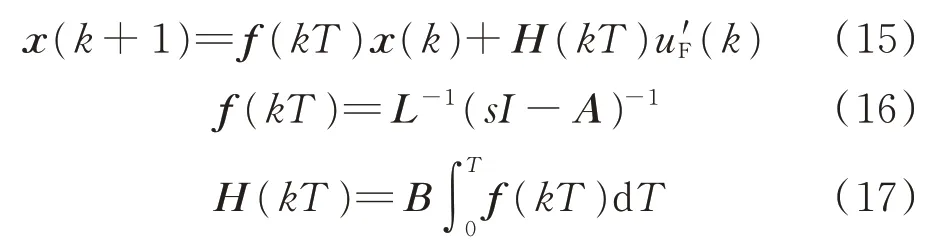
式中：T 為采樣周期；L-1(?)表示拉普拉斯逆變換。

將f (kT )和H(kT )組合，得到初始預測矩陣，如式（18）所示，其中ω1和ω2為雙調諧無源濾波器的諧振角頻率。

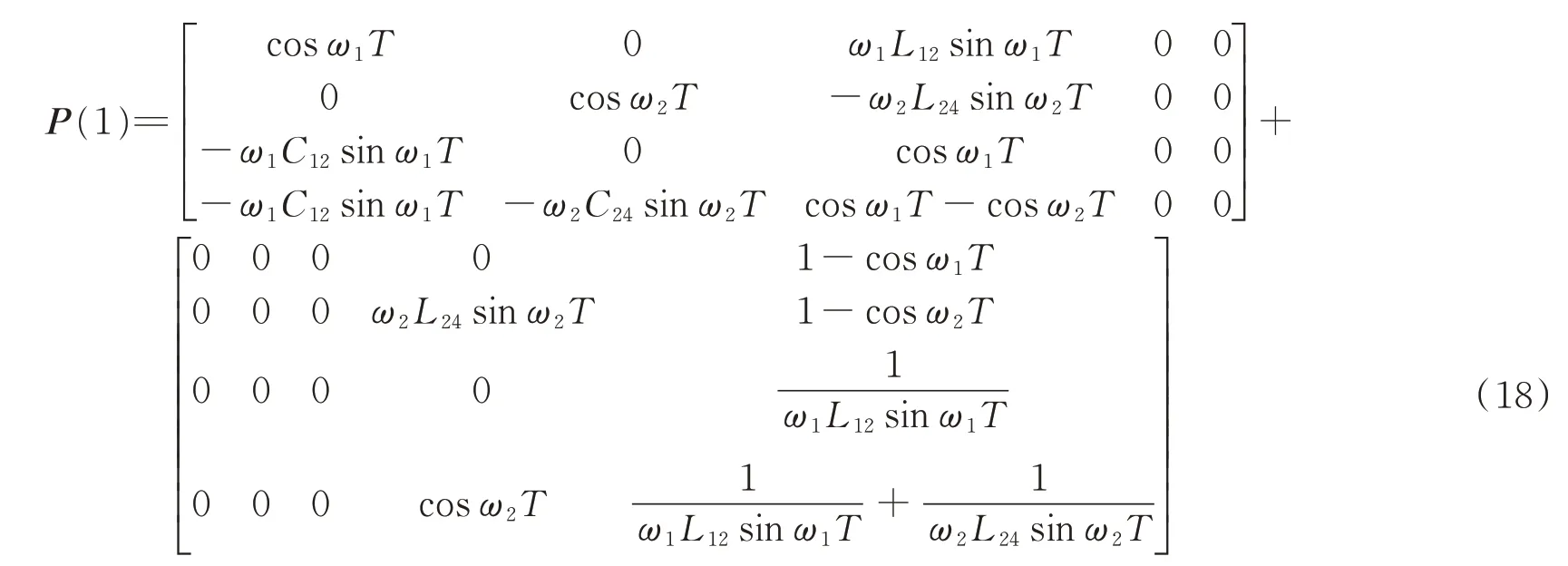
可知，初始預測矩陣和電路參數緊密相關，在迭代過程中，不斷通過采樣值修正預測矩陣，因此，即使實際參數有偏差，算法也能收斂到適應系統的值。

4 仿真驗證

4.1 系統參數

采用PSCAD/EMTDC 仿真軟件驗證HAPF的濾波效果以及所提諧振抑制策略的有效性，HAPF 及LCC-HVDC 系統參數如附錄B 表B1所示。

LCC-HVDC 系統的傳輸功率為1 000 MW，直流電壓為500 kV，整流側的無功功率缺額為625 Mvar。其中，HAPF 補償250 Mvar，其余無功部分由電容器組補償。根據電力系統設計規程，換流母線暫態電壓變化率在無功分組發生投切時應小于1.5%［23］，因此，按照交流側短路容量可估計電容器小組容量為37.5 Mvar。

4.2 濾波效果分析

HAPF 投運前后的負載電流、電網電流及其總諧波畸變率（total harmonic distortion，THD）見附錄A 圖A5、圖A6 和附錄B 表B2，由圖表可知，HAPF投運前LCC-HVDC 負載電流畸變嚴重，THD 達5.358%。HAPF 投運后，負載各次諧波含量均降低，THD 為0.172%。HAPF 輸出的補償電流和負載諧波電流對比圖見附錄A 圖A7，說明HAPF 具有良好的濾波能力。

4.3 諧振抑制性能驗證

4.3.1 控制延時對穩定性的影響

為驗證不同控制延時下系統和HAPF 的諧振規律，分別設置延時為150、180、230 μs。不同延時對應的電網三相電壓見附錄A 圖A8。

當系統延時小于150 μs 時，系統穩定，電網電流基本不含諧波分量；當延時增大到180 μs 時，系統在高頻處發生諧振，主要集中在29 次、30 次和31 次諧振。當控制延時增大至230 μs 時，諧振嚴重程度加深，諧振次數減小為28 次，與幅頻特性中阻抗交點對應的頻率基本一致。仿真結果表明，系統延時過大，將對系統穩定性造成嚴重的影響，但目前較難通過減少器件的死區效應或提高采樣頻率來降低延時，因此考慮采用控制算法來等效縮短延時時間。

換流母線的公共耦合點處共連接4 個子系統，即交流系統、無功補償系統、濾波系統和負載。當延時為180 μs 時，各個子系統的A 相電流見附錄A圖A9。

濾波和無功補償支路29 次諧波電流的幅值很大，且兩者等大反向，說明在控制延時的影響下，HAPF 和并聯電容器阻抗相互匹配，發生諧振，由于阻抗的分流特性導致交流系統和負載同時引入29 次諧波電流。

4.3.2 諧振抑制策略驗證

設置無延時情況以及考慮150、180、230 μs 延時情況下引入3.2 節提出的諧振抑制策略的仿真試驗，結果如圖5 所示。

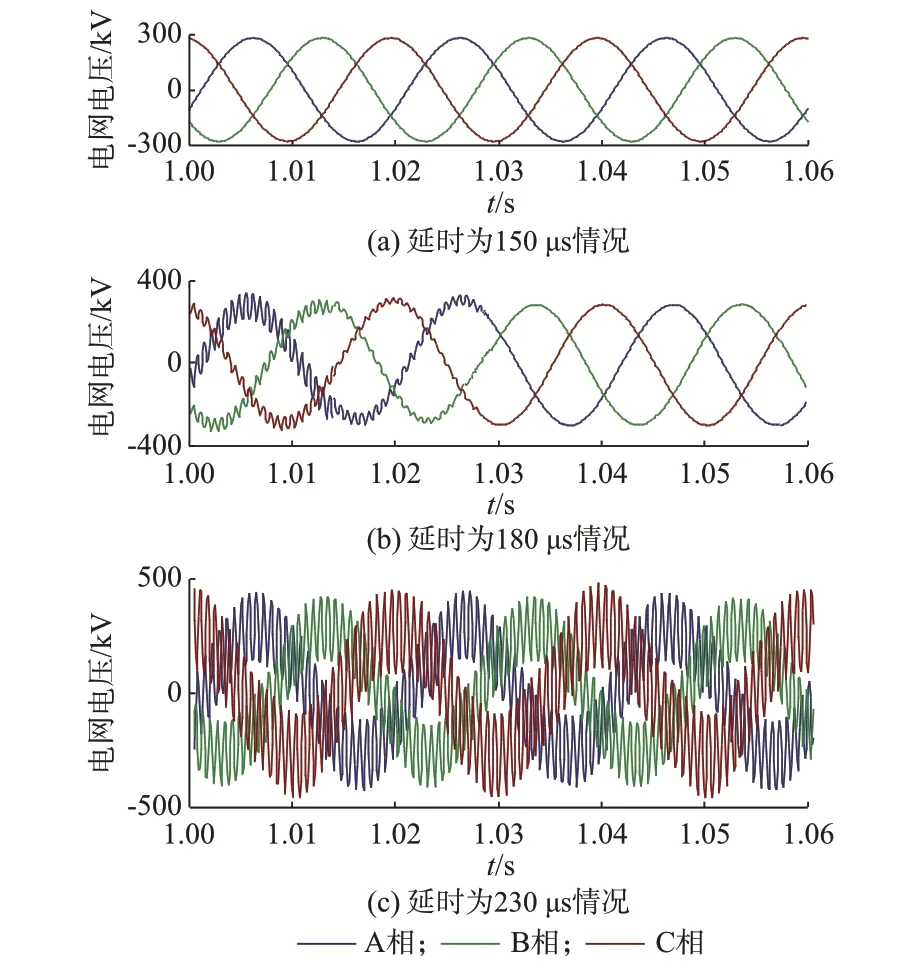
圖5 不同延時下電網電壓波形Fig.5 Power grid voltage curves with different delays

當無延時或延時為150 μs 情況下，系統不發生諧振，HAPF 濾波效果良好；當延時為180 μs 時，系統發生諧振，且諧振抑制策略在一個周期內有效抑制了諧振，驗證了諧振抑制策略的有效性；當延時為230 μs 時，系統發生諧振，但是諧振抑制策略失效。由算法原理可知，預測波形的超前量由仿真中的控制周期決定，本文控制周期為50 μs，因此可有效抑制延時小于230 μs 的諧振情況。

4.4 諧振抑制自適應性能驗證

4.4.1 電路參數自適應

為驗證抑制算法的自適應性能，選取偏差電容電感設定值10%的值作為計算參數，根據式（18）和附錄B 表B1 中參數計算LMS 算法中初始預測系數矩陣，所得數值見附錄B 表B3。

在仿真t=0.5 s 處引入預測環節，交流系統三相電壓、電流波形如附錄A 圖A10 所示，即使在實際工程中由于器件老化引起的電容電感參數與標稱值不符，系統仍可穩定運行。諧振抑制算法在半個至一個周期內即可有效抑制因控制延時引起的諧振。

經過不斷迭代后的預測誤差如附錄A 圖A11所示。由于參數不完全匹配，一開始存在較大誤差，隨著不斷修正迭代，誤差在一個周期后趨近于零，驗證了算法的參數自適應能力。

不同電容電感值下的迭代時間見附錄B 表B4。當參數無偏差時，迭代時間為0.003 s，是因為系統發生諧振，諧振電流波形不穩定，存在一定的誤差；當參數偏差度越來越大時，迭代時間隨之增加，當參數精確度為80%時，誤差在0.023 s 的迭代時間內達到較為理想的情況。

4.4.2 工況自適應

在仿真t=0.54 s 處降低20% 系統輸送功率，4 個子系統的A 相電流波形見附錄A 圖A12。當系統輸送功率降低20%時，負載電流和系統電流下降，HAPF 仍可穩定有效濾除諧波，系統動態性能良好，驗證了諧振抑制策略對不同工況的良好適應性。

4.4.3 電容器投切自適應

由圖4 可知，系統諧振次數由系統阻抗和HAPF 阻抗幅值交點對應的頻率決定，當延時為180 μs，且系統并聯電容器發生投切時，系統諧振次數將發生偏移。仿真中在t=0.6 s 處切除一組電容值為1 μF 的電容器，電容電流波形見附錄A 圖A13。當系統發生電容器投切時，系統仍能穩定運行，不發生諧振，驗證了諧振抑制算法在電容器發生動態投切情況下的自適應能力。

5 結語

本文重點研究了基于級聯H 橋的HAPF 及其諧振抑制策略，得到如下結論：

1）HAPF 拓撲采用12 次和24 次雙調諧濾波器代替12 次和24 次單調諧并聯的形式，更貼合實際工程，可適用于高壓大容量諧波濾除的場合，濾波效果良好。

2）建立了包含實際控制延時環節的HAPF 阻抗模型，分析了HAPF 阻抗及電網阻抗的頻率特性，得到了控制延時與混合有源濾波系統的諧振規律。

3）基于LMS 算法的自適應諧振抑制策略不需要信號的統計特征且計算復雜度低，通過預測電流波形，等效補償了控制延時，從而消除了HAPF 的負阻抗特性。仿真結果表明，該方法在一個周期內有效抑制了諧振，并且能自適應調整預測矩陣，使其適用于電路參數變化以及發生電容器投切的情況，具有良好的穩態和動態性能。

本文研究的諧振抑制策略適用于HAPF 需要補償的控制延時小于一個控制周期的情況，而對更長延時引起的諧振問題及其抑制措施還需進一步研究。

附錄見本刊網絡版（http：//www.aeps-info.com/aeps/ch/index.aspx），掃英文摘要后二維碼可以閱讀網絡全文。