直線遞減期累計產量新模型的建立與應用
——以靖安油田五里灣開發區為例

康志勇，周明旺，曾憲紅，李曉濤，閆鑫洋

（中國石油遼河油田分公司勘探開發研究院，遼寧盤錦 124010）

Arps 于1945 年提出的三種遞減類型（指數遞減、雙曲線遞減和調和遞減），即傳統Arps 遞減理論已在國內外得到廣泛應用[1–6]，其中指數遞減應用最為普遍，如DeGolyer and MacNaughton 等國際咨詢公司普遍采用指數遞減預測產量。2004 年以來，從事開發研究的科研人員逐漸將傳統Arps 遞減理論擴展為廣義Arps 遞減理論，即將傳統Arps 遞減指數的應用范圍由[0，1]擴展到（–∞，+∞），并導出廣義Arps遞減理論之直線遞減期累計產量公式[7–12]（以下簡稱老模型）。為了解決老模型中由于存在明顯系統誤差，預測精度有限的問題，本文依據直線遞減的特點，系統建立了累計產量和技術可采儲量理論 方程（以下簡稱新模型）。新模型計算方法簡便快捷、計算精度高于廣義Arps 遞減理論導出的直線遞減期累計產量和技術可采儲量公式，從而為客觀評價累計產量及技術可采儲量提供了有效的實現途徑和廣闊的應用前景。

1 直線遞減模型的建立

1.1 直線遞減的特點

直線遞減是指產量遞減呈線性變化，且有如下特點：一是任何統計單位的產量遞減指數恒為- 1；二是直線遞減期穩定日產量、穩定月產量或穩定年產量均為等差數列，即任意兩個相鄰穩定產量之間的差值為常數（穩定日產量數列的等差為q0Ddi、穩定月產量數列的等差為m2q0Ddi或Q0Dmi、穩定年產量數列的等差為(12m)2q0Ddi或Q0Dyi）。根據直線遞減的特點可導出系列遞減參數的相關數學表達式。

1.2 穩定產量

根據穩定產量直線遞減數列的等差可導出產量遞減生產到第t 天（或第x個月或第y 年）的穩定產量數學表達式：

式中：tq 為遞減生產第t 天的穩定日產量，m3或t；q0為初始穩定日產量，m3或t；t 為遞減生產天數，d； Ddi為初始日遞減率。

當式（1）中遞減生產時間為月時，相應產量為月產量，遞減率為初始月遞減率；當遞減生產時間為年時，相應產量為年產量，遞減率為初始年遞減率。其中，初始月產量和初始年產量與初始穩定日產量和初始日遞減率等參數之間存在固定函數關系：

式中：Q0為初始月產量，m3或t；Q0為初始年產量，m3或t；m為平均每個月遞減生產天數（31 1＜≤m），d。

對于無穩產期的評價單元，初始月產量和初始年產量為虛擬產量，計算累計產量時不能將初始月產量或初始年產量直接計入遞減前的累計產量中。

1.3 初始遞減率

根據初始遞減率定義[7]和評價單元直線遞減生產特點可采用任意相鄰穩定日產量或相鄰穩定月產量或相鄰穩定年產量導出的初始日遞減率的數學表達式：

式中：1+tq 為遞減生產第 1+t天的穩定日產量，m3或t；Qx、Qx+1分別為遞減生產第x個月、遞減生產第x+1個月的穩定月產量，m3或t；x為遞減生產日歷月數，mon；yQ 、1+yQ 分別為遞減生產第y 年、遞減生產第1+y年的穩定年產量，m3或t； y 為遞減生產日歷年數，a。

計算初始月遞減率或初始年遞減率所用公式形式與式（4）相同，只需將遞減時間和產量單位進行相應變化。

1.4 遞減期累計產量和技術可采儲量

采用初始穩定日產量或初始月產量或初始年產量可導出直線遞減期累計產量數學表達式：

式中：Np遞減生產第t 天（或遞減生產第x 個月或遞減生產第y 年）的累計產量（不含0q 及之前產量），m3或t。

當式（7）中的遞減生產時間為月時，相應產量為初始月產量，遞減率為初始月遞減率；當遞減生產時間為年時，相應產量為初始年產量，遞減率為初始年遞減率。

根據產量直線遞減生產的特點可分別得到技術極限遞減生產天數、技術極限遞減生產日歷月數和技術極限遞減生產日歷年數的數學表達式：

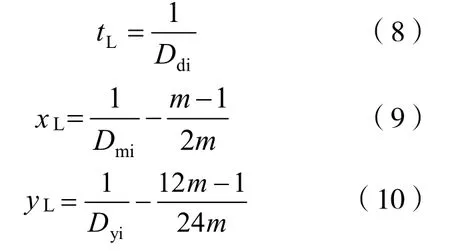
式中：tL為技術極限遞減生產天數，d；xL為技術極限遞減生產日歷月數，mon；yL為技術極限遞減生產日歷年數，a；miD 為初始月遞減率；yiD 為初始年遞減率。

將技術極限遞減生產時間方程與直線遞減期累計產量方程結合可導出技術可采儲量數學表達式：

式中：RTN 為原油技術可采儲量，m3或t；oN 為評價單元遞減生產前原油累計產量，m3或t。

當式（11）中的技術極限遞減生產時間為月時，相應產量為初始月產量，遞減率為初始月遞減率；當技術極限遞減生產時間為年時，相應產量為初始年產量，遞減率為初始年遞減率。

1.5 直線遞減模型適用性分析

嚴格地講，遞減指數等于1- 的評價單元均可采用直線遞減模型評價遞減期穩定產量和累計產量，但實際評價單元在遞減生產過程中不完全遵循單一遞減規律，特別是遞減初始階段呈直線遞減的評價單元，到遞減中后期并不一定依然遵循直線遞減特點。因此，用直線遞減模型預測評價單元產量時，產量變化要遵從持續、穩定、規律性變化的原則。

對于相鄰穩定產量的差值大于平均差值%10±的評價單元，原則上不采用直線遞減模型預測產量；對于遞減生產到中后期的評價單元，用直線遞減模型預測產量相對客觀準確；對于只有較少初始產量遞減生產數據的評價單元，盡管遞減指數等于或近似等于 1- ，用直線遞減模型預測評價單元中后期產量數據仍存在風險。

2 新老模型對比

當遞減指數為1- 時，廣義Arps 遞減理論之直線遞減期原油累計產量公式為[7–11]：

采用月產量或年產量計算遞減期累計產量公式形式與式（12）相同，只需將遞減時間、穩定產量、初始遞減率等進行相應變化。

若評價單元直線遞減期平均每個月遞減生產25 d，則穩定日產量、穩定月產量、穩定年產量及遞減期原油累計產量列于表1。分別采用老模型和新模型計算遞減生產第900 天、遞減生產第36 個月和遞減生產第3 年的原油累計產量及誤差情況。

根據表1 給出的理想直線遞減生產數據可得到日、月、年的初始產量及初始遞減率：初始日產量為50.00 m3、初始日遞減率為0.001；初始月產量為1 265.00 m3、初始月遞減率為25/1 012；初始年產量為17 242.50 m3、初始年遞減率為600/2 299。

表1 直線遞減生產數據表

采用新模型和老模型所計算的評價單元累計產量及誤差對比情況如表2 所示。

表2 新老模型預測累計產量及誤差對比

新模型計算遞減期累計產量與實際產量完全吻合；老模型計算遞減期累計產量均有誤差，且以穩定年產量預測累計產量誤差最大可達27.30%，用穩定日產量預測累計產量誤差最小為0.09%。

3 應用實例

靖安油田五里灣開發區產層為三疊系延長組6段，1996 年投入試采，2000 年轉入開發。該開發區投產第9 年進入直線遞減期，歷年年產量及累計產量情況詳見圖1 和表3。

圖1 五里灣開發區生產曲線

該開發區遞減前累計產量206.57×104t，根據直線遞減期相鄰穩定年產量差值相等的特性，計算直線遞減期相鄰穩定年產量間的平均差值為1.22×104t，則據式（13）計算可得初始年產量為39.49×104t。

式中：Q1為遞減生產第1 年的穩定年產量，據實際資料取值為38.27×104t；yQΔ 為直線遞減期相鄰穩定年產量間的平均差值，t。

由前述可知：

將式（13）與式（14）聯立可解得初始年遞減率為489/15797（或0.03）。

將初始年遞減率和初始年產量分別代入式（1）和式（7）得穩定年產量和累計產量預測值（表3），預測值與實際生產數據相吻合。

表3 五里灣開發區實際遞減生產數據及預測數據對比

五里灣開發區平均每個月遞減生產天數10～30 d，其遞減期技術極限遞減生產年數和開發區技術可采儲量分別為31.806 a 和824.87×104t。

采用老模型計算五里灣開發區累計產量最大誤差為3.36%，用新模型計算累計產量最大誤差為1.22%（表4）。

已知該開發區探明地質儲量6 067.00×104t，由此計算技術可采儲量采收率為13.6%。

表4 五里灣開發區新模型與老模型預測產量誤差對比分析

4 結論

（1）新模型和老模型分別導出的遞減期累計產量及技術可采儲量公式不同，計算精度差異明顯：對理想直線遞減數據而言，新模型計算相對誤差遠小于老模型計算的相對誤差；對實際直線遞減生產數據，新模型計算累計產量最大誤差為1.22%，老模型計算累計產量最大誤差為3.36%；新模型不僅是對廣義Arps 遞減理論的補充與完善，在實踐中還具有廣泛的實用性，且理論基礎扎實可靠。

（2）新模型應用初始穩定日產量和初始日遞減率等較易獲取的參數可直接計算初始月產量和初始年產量，與回歸法相比，極大地提升了初始產量的計算精度。

（3）新模型采用極限遞減生產時間和初始產量及初始遞減率計算可采儲量，不僅計算方法簡便實用，計算精度也得到了顯著提高。