一種多彈協同制導策略

花文濤，劉沛文，賈曉洪，梁曉庚

(中國空空導彈研究院 航空制導武器航空科技重點實驗室， 河南 洛陽 471009)

隨著智能技術、自組網技術的快速發展，多導彈協同攻擊將成為未來戰場上的主要作戰模式之一。通過多導彈間的協同探測、通信、飛行、攻擊，使得體系探測、突防與抗干擾能力大大增強，另一方面這種協同方式通過彈群攻擊目標，一定程度上降低了單枚導彈功能、性能的要求，實現了低成本導彈對高成本目標的毀傷[1-4]。

多導彈協同探測、攻擊技術由于存在上述一系列優勢近些年已成為國內外研究的熱點。文獻[5-10]研究通過預設相同飛行時間實現多導彈的協同攻擊，缺點是各個導彈時間開環控制，導彈預設時間過大或過小都可能導致制導律失效；文獻[11-14]無需發射前設置攻擊時間，通過飛行過程中對彈間剩余飛行時間信息的通信協調，最終實現對目標的一致性攻擊，但文獻大多考慮協同攻擊靜止目標，具有很大的局限性。本文在對動目標攻擊最優制導律分析的基礎上，設計一種多彈協同制導律，分析導彈剩余飛行時間估計方法和領彈與從彈選擇策略，實現對動目標協同攻擊。

1 協同制導律

1.1 帶角度約束最優制導律

最優制導律設計最終可歸結為攔截控制問題，即以最小的控制能量攔截目標。其中，帶角度約束最優制導律，除了保證末端最小脫靶量，導彈與目標視線之間還可以設計成給定夾角，形成多枚彈不同攔截態勢，以提高殺傷效能。

導彈的彈目運動關系如圖1所示：

圖1 彈目運動關系框圖

攔截狀態方程

(1)

其中：

攔截的二次性能指標：

(2)

S、R為任意給定的狀態加權系數，一般S取實對稱半正定矩陣，R取實對稱正定矩陣。

采用伴隨方法[15]和最優控制理論可以得到攔截問題的閉環解析解。

(3)

其中，M為狀態方程的伴隨式(4)的解。

(4)

(5)

(6)

1.2 協同制導律

從二次性能指標式(2)可以看出，導出的最優比例制導律式(6)和角度約束最優制導律式(5)均在滿足攻擊要求下實現了控制能量最小，導彈彈道剛度最大，即導彈在最短的時間內對目標進行攻擊或攔截。

與傳統單枚導彈最優導引律不同，考慮時間約束下的多彈協同制導更加注重多枚彈到達時間上盡可能的一致性，為保證達到時間協同的效果，從彈將不得不消耗更多的控制能量。另外，文獻[16-17]指出為實現導彈時間約束導引律，需要控制兩個參數：彈-目視線角速度和導彈最終碰撞時間。而實際上對動目標攻擊而言，由于目標運動的不確定性，導彈最終碰撞時間(導彈總飛行時間)無法在發射前提前指定，而單個導彈攻擊目標的剩余飛行時間卻很容易根據彈目運動信息估算得到。因此本文在文獻[17]的基礎上，提出基于剩余飛行時間設計的一種偏置比例導引法，實現導彈間攻擊時間的協調。

為實現協同時間攻擊，引入控制時間修正量

(7)

當時間修正量為正時，表明從彈估計的剩余飛行時間大于領彈的剩余飛行時間，此時從彈宜按照最優導引律飛向目標，使得從彈飛行時間最小；當時間修正量為負時，表明從彈的剩余飛行時間小于領彈的剩余飛行時間，應在從彈控制指令中加入反向補償項，導彈以一定曲率反向飛行，使得從彈飛行時間增大。通過引入時間修正量，盡可能地實現領彈和從彈攻擊時間上一致。

考慮時間協同的偏置比例導引律：

(8)

K為導引律導航系數，根據時間精度要求和過載要求進行調整。導航系數越大，協同的控制時間精度越高，過載需求也越大。當時間修正量為正時，Δt>0，從彈制導律退變為比例導引n=aC2。

類似地，考慮角度-時間約束的協同制導律為：

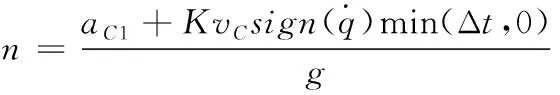
(9)

2 剩余飛行時間估算

剩余飛行時間估算是協同制導律實現的前提。目前剩余飛行時間估算算法主要有直接解析法和迭代遞推法。直接解析法計算量小，但估計精度低，大多從攔截制導律方程進行推導，因而多用于攻擊靜止目標和典型運動目標[5，6，10，18-20]。迭代遞推法由于實時引入測量估計狀態進行修正，估計精度高，尤其適合用于攻擊運動目標。

剩余飛行時間估算需計算當前時刻到命中點時刻導彈與目標間的平均相對加速度在視線上的分量A。在此條件下，剩余飛行時間滿足下式

(10)

R為當前時刻彈目距離，式(10)的唯一有意義的解為

(11)

(12)

3 領彈與從彈的初步選擇

(13)

式(13)中，vM為導彈速度;ηM，max為導彈最大速度前置角(離軸角)；vT為目標速度；ηT為目標速度前置角。可行域的下限tgo，min為導彈實時估算的剩余飛行時間，可行域的上限tgo，max受導彈最大離軸角的限制。

根據剩余飛行時間的可行域，可以在飛行中實時確定領彈和從彈，具體方法為：取多枚彈中可行域交集最多的導彈為領彈，與之時間有交集的導彈為從彈，無交集的導彈則構建新的彈群或以非協同方式按最優導引律自主攻擊目標。

4 仿真與分析

4.1 時間協同仿真

本組仿真用于實現3枚導彈對同一目標進行時間協同攻擊。初始仿真參數如表1所示。如果采用式(6)比例導引(PNG)，則3枚彈擊中目標的時間分別為13.62 s、14.69 s、17.38 s，彈道曲線如圖2所示。采用協同制導律，3枚彈根據可行域自適應調整飛行時間，擊中目標時間分別為18.69 s、18.65 s、18.58 s，仿真曲線如圖3～圖5，滿足了協同攻擊的要求。

表1 時間協同攻擊初始參數

圖2 比例導引下彈道曲線

圖3 協同制導下彈道曲線

圖4 剩余飛行時間曲線

圖5 協同制導下的領彈選擇曲線

4.2 角度-時間協同仿真

本組仿真用于實現3枚導彈對同一目標進行角度-時間協同攻擊。仍采用表1所示初始條件，指定3枚彈擊中目標的末端角度約束分別為-50°、100°、-30°。如果采用式(5)角度約束最優制導律，則3枚彈擊中目標的時間分別為13.94 s、17.37 s、19.01s，采用角度-時間協同制導律，3枚彈擊中目標時間為19.54 s、19.82 s、19.69 s，命中角度為-50.68°、99.96°、-30.65°，仿真曲線如圖6-圖8，滿足角度-時間協同攻擊要求。

圖6 協同制導下彈道曲線

圖7 剩余飛行時間曲線

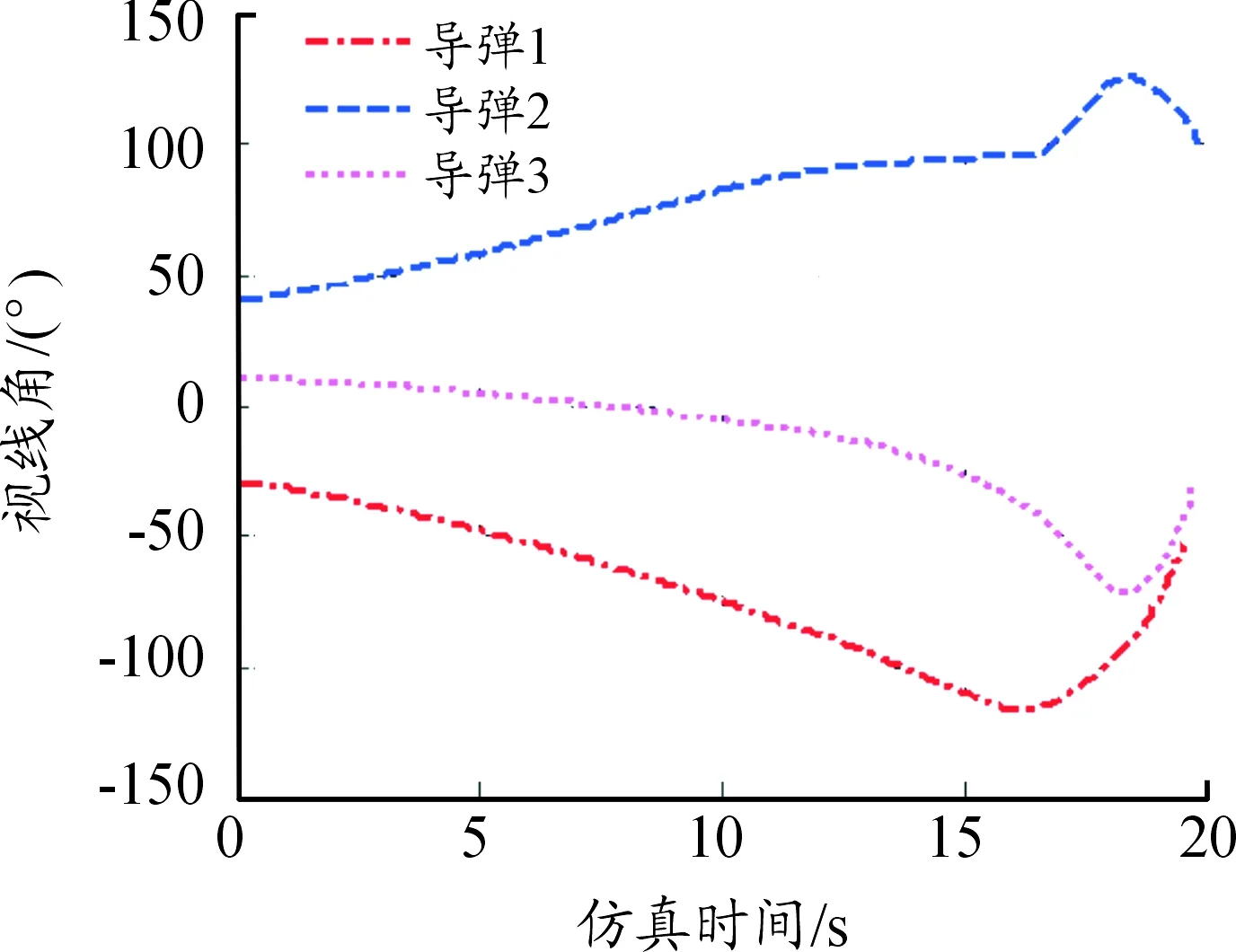
圖8 協同制導控制末端視線角曲線

5 結論

1) 在最優導引律分析的基礎上，給出了一種協同制導律形式，該制導律適合領彈-從彈條件下，從彈攻擊時間和角度根據領彈剩余時間和末端攻擊要求實時調整；

2) 通過分析導彈攻擊時間的可行域，提出領彈從彈在線選擇方法，經仿真，該方法可以實時確定領彈和從彈選擇策略；

3) 給出攻擊運動目標剩余飛行時間的方法。通過時間協同仿真和角度-時間協同仿真，驗證了所提出的多彈協同制導策略的有效性。