一種基于多彈協同定位的機動目標估計算法

何金剛，高 剛

(中國空空導彈研究院， 河南 洛陽 471009)

隨著新型推力矢量渦扇發動機、先進氣動設計、雙向數據鏈和隱身技術的應用，第四代戰斗機和無人作戰飛機等新一代航空武器相繼出現，使得在未來戰爭中空空導彈將面臨機動能力更強、逃逸方式更復雜、可探測性更差的攻擊目標[1-2]。另一方面，隨著技術發展，空空導彈的彈間組網技術逐漸具備了應用可能。近年來，多導彈協同攻擊[3]以其特有的優勢正在受到越來越多的關注。在進攻方面，多彈協同制導可以通過彈群協同，將多枚導彈融合成一個信息共享、功能互補、戰術協同的作戰群體，利用群體優勢對敵防御體系和目標進行多層次、全方位的打擊，實現攻擊效能的整體提升[4-5]。

本文利用多導彈協同攻擊體系，根據雙彈協同角度定位結果，構造距離偽量測信息，將測量方程進行擴維，以改善純角度跟蹤系統中目標估計精度，最終實現減小脫靶量的目的。

1 多彈協同體系中被動跟蹤系統設計

被動雷達在跟蹤機制上屬于純方位跟蹤，僅對目標的方位進行測量，不能測距，目標運動狀態方程和觀測方程不可能都是線性的，使得傳統的線性濾波方法不適用于被動雷達目標跟蹤問題[6-8]。其次，被動雷達目標跟蹤是從含有觀測噪聲的角度測量序列中估計目標的運動狀態參數(包括位置、速度和加速度等)，經研究證明，僅利用測角信息對目標進行無源被動定位，有效估計出目標的運動狀態參數，這有較為苛刻的可觀測性條件限制，在單觀測平臺對運動目標定位時，要求觀測平臺做特殊的機動運動，并且機動運動的航路直接影響著目標運動要素的收斂速度和精度。這一苛刻的可觀測性條件同樣限制了被動雷達目標跟蹤的工程化應用。

多彈協同體系中可充分發揮多枚被動導彈的多角度觀測優勢，利用角度信息進行協同定位，得到目標狀態信息[9]。測向定位法的基本原理是利用多部接收雷達測得的方位信息或一個運動的接收雷達在不同時間測得的多條方位信息交叉對目標定位[10-11]。二維平面空間的測向定位法，如圖1 所示。兩部雷達對回波信號進行檢測與信號處理，可分別得到目標相對于測量點的方位角。雷達測得方位角后，可知目標的實際位置在以本雷達為起點，以方位角為方向角的射線上。兩部雷達同時測量時，目標的位置處于兩條射線的交點上，由此即完成對目標定位[12-17]。

圖1 測向定位法原理示意圖

通常被動跟蹤中，觀測量為方位角、俯仰角，根據協同測向定位得到彈目相對距離后，可將此作為偽觀測量引入測量方程。測量方程擴維后再進行濾波處理，得到可供制導使用的目標信息。系統原理如圖2所示。

圖2 基于協同定位的被動跟蹤系統原理框圖

2 基于多彈協同定位的目標估計算法

2.1 協同定位算法

兩枚導彈進行協同定位時，不考慮各種誤差的理想情況下，目標位于兩條視線交點處。然而，由于導航誤差、測量誤差等影響，實際系統中兩條視線不會相交。那么在該情況下，認為目標點是相距兩條方位線最近的點，因此本文設計的協同定位算法思想為：實際目標點到兩條方位線二階距的和最小。

設空間兩條視線(方位線)的方程為A和B，其形式分別表示為：

式(1)、(2)中：[xM1yM1zM1]T和[xM2yM2zM2]T是慣性空間中兩枚導彈的位置：分別記為XA和XB，[α1β1γ1]T和[α2β2γ2]T是兩枚導彈測量的視線方向余弦。

目標點是同時對方程A和B二階距之和最小的點，即：

(3)

由于點到直線的二階距即為點到直線距離的模的平方，因此交叉定位算法又可以描述為：確定目標點X=[xTyTzT]T，使式(4)最小，即：

(5)

式(4)中，d1和d2是空間中某點到A、B兩條直線的距離。即：

min[f(x，y，z)]|(xT ，yT ，zT )

(5)

根據點到直線的距離公式，有：

(6)

將式(6)寫成反對稱陣的形式，有：

(7)

記：

有：

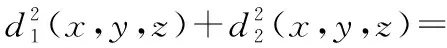
(8)

X=(VTV+WTW)-1VTVXA+

(VTV+WTW)-1WTWXB

(9)

式(9)即為協同定位算法確定的目標點坐標。有了協同定位的目標點坐標，即可得到每一枚導彈的彈目距離信息估值，將此信息作為偽量測信息進行目標狀態估計。

2.2 目標估計算法

2.2.1目標運動模型

機動目標模型是通過數學描述目標真實運動，是目標跟蹤的重要要素之一，目標運動描述越準確反應目標的實際運動，對目標狀態估計效果越好。描述目標運動常用的模型有CV模型，CA模型，Singer模型，機動目標“當前”統計模型等。

機動目標“當前”統計模型是一種采用零均值和修正瑞利分布表征機動加速度特性的時間相關模型，在具體的場景下，該模型僅需考慮目標在當前條件下的機動可能性，即機動加速度的當前概率密度，這樣機動加速度的取值范圍大大減小。大量實驗表明，該算法在跟蹤機動目標時具有良好的跟蹤結果[18]。

可以描述如下：

(10)

對應的離散時間形式為：

(11)

2.2.2混合量測模型

導引頭一般在球坐標系下測量目標信息，而狀態方程一般在直角坐標系下建立。因此卡爾曼濾波的狀態方程和量測方程勢必存在一定的耦合，需要對量測方程進行線性化，得到線性卡爾曼濾波器，便于工程應用。根據導引頭測量的失調角、框架角和導彈姿態，求取導引頭測量視線相對于慣性空間的高低角和方位角。并根據多彈協同定位結果得到彈目距離信息估值作為偽量測信息，建立混合量測方程。

(12)

協同定位獲得的目標位置誤差受兩部分誤差影響，一是導引頭測量的角噪聲，另一部分是導航系統產生的位置誤差。當這兩種誤差滿足正態分布并相互獨立，則測量方差滿足疊加關系。根據數據融合理論，偽距離量測噪聲可寫為：

(13)

所建立的卡爾曼量測方程為非線性方程，對量測方程在k時刻進行線性化，得到：

(14)

展開得：

(15)

2.2.3濾波算法

系統的狀態方程是線性的，不存在線性誤差。但是測量方程是非線性的，因此采用擴展卡爾曼濾波進行目標狀態估計。基本卡爾曼濾波實現原理如圖3所示。

圖3 卡爾曼濾波實現原理框圖

3 仿真分析

在Matlab中建立跟蹤系統模型，對該算法進行仿真分析。導引頭測量特性設置為：方位角和高低角觀測噪聲均方誤差分別為σα=0.2°和σβ=0.2°。

仿真基本條件如下：導彈M1與目標距離15 km，目標迎頭進入速度300 m/s，10 s時開始以3g水平過載做S機動；導彈M2視線在空間保持與導彈M1視線夾角30°，并將其觀測信息實時傳送至導彈M1。導彈M1的狀態估計誤差如圖4～圖7所示。

圖4 偽量測量彈目距離估計誤差曲線

圖5 目標位置估計誤差曲線

圖6 目標速度估計誤差曲線

圖7 目標加速度估計誤差曲線

通過仿真結果可見，雙彈目標定位誤差隨彈目距離接近不斷減小，8 km內距離誤差已收斂至50 m以內。將雙彈協同定位的結果作為偽量測信息得到的目標狀態估計結果精度較高。X方向為目標接近方向，目標狀態估值誤差主要反映了偽量測信息的誤差。

4 結論

本文考慮了分布式協同體系中信息資源優勢，利用多彈協同對目標進行定位，并作為偽量測信息引入目標跟蹤濾波器中。通過理論分析與數字仿真驗證，證明了該方法的有效性。本文提出的技術方法可應用于多紅外或被動雷達導引頭協同探測系統中，也可應用于雷達型導彈距離測量受干擾時的制導信息估計算法。后續將進一步考慮協同體系中影響協同定位的因素以及不同偽量測信息精度下濾波器設計問題。