基于深度卷積神經網絡的多飛行器構型保持研究

槐澤鵬，王洪波，龔 旻

(中國運載火箭技術研究院， 北京 100076)

2016年“人工智能”被寫入我國“十三五”規劃，2017年國務院發布《新一代人工智能發展規劃》，在頂層文件驅動下，社會各行各業都在加大對人工智能的研究與投入。深度學習作為通向人工智能的途徑之一[8]，已經在圖像識別[2，9-10]、語音識別[11-12]、文本識別[13-14]、多模態交互[15]等領域取得諸多成果。尤其是谷歌舉辦的ImageNet比賽：從2012年的AlexNet[3]，到2013年的ZF Net[4]，2014年的VGGNet[5]、GeogleNet[6]，再到2015年的ResNet[7]，這些對深度學習的發展具有里程碑式意義。同時，如Facebook、Microsoft、Amazon等企業開發了第三方深度學習框架以支撐相關學者的研究，如TensorFlow、MXNet，Caffe、Keras等，這些為深度學習在其他行業的普及和應用奠定了良好基礎。

在國防軍工領域，協同作戰是近些年來興起的被認為具備非對稱領先優勢的新作戰模式，世界各軍事大國都在開展相關研究和項目，如空中協同作戰SoSITE[20]、拒止環境協同作戰CODE[21]、無人機協同作戰“山鶉”Perdix[22]等。多飛行器協同是協同作戰發展的必然趨勢，當前此方向的研究主要集中于關鍵技術攻關，如任務規劃技術[17]、飛行器數據鏈技術[18]、協同路徑規劃技術[19]等，其中構型保持對實現多種飛行器編隊模式具有基礎支撐意義[16]。因此，本文旨在將深度學習技術應用于多飛行器構型保持問題，以獲得性能更加良好的構型保持算法。

1 問題描述及飛行器模型

本文旨在解決以下問題：3枚飛行器在中段飛行時在當地鉛錘面內持續保持正三角形構型，如圖1所示。保持的構型如圖2所示。

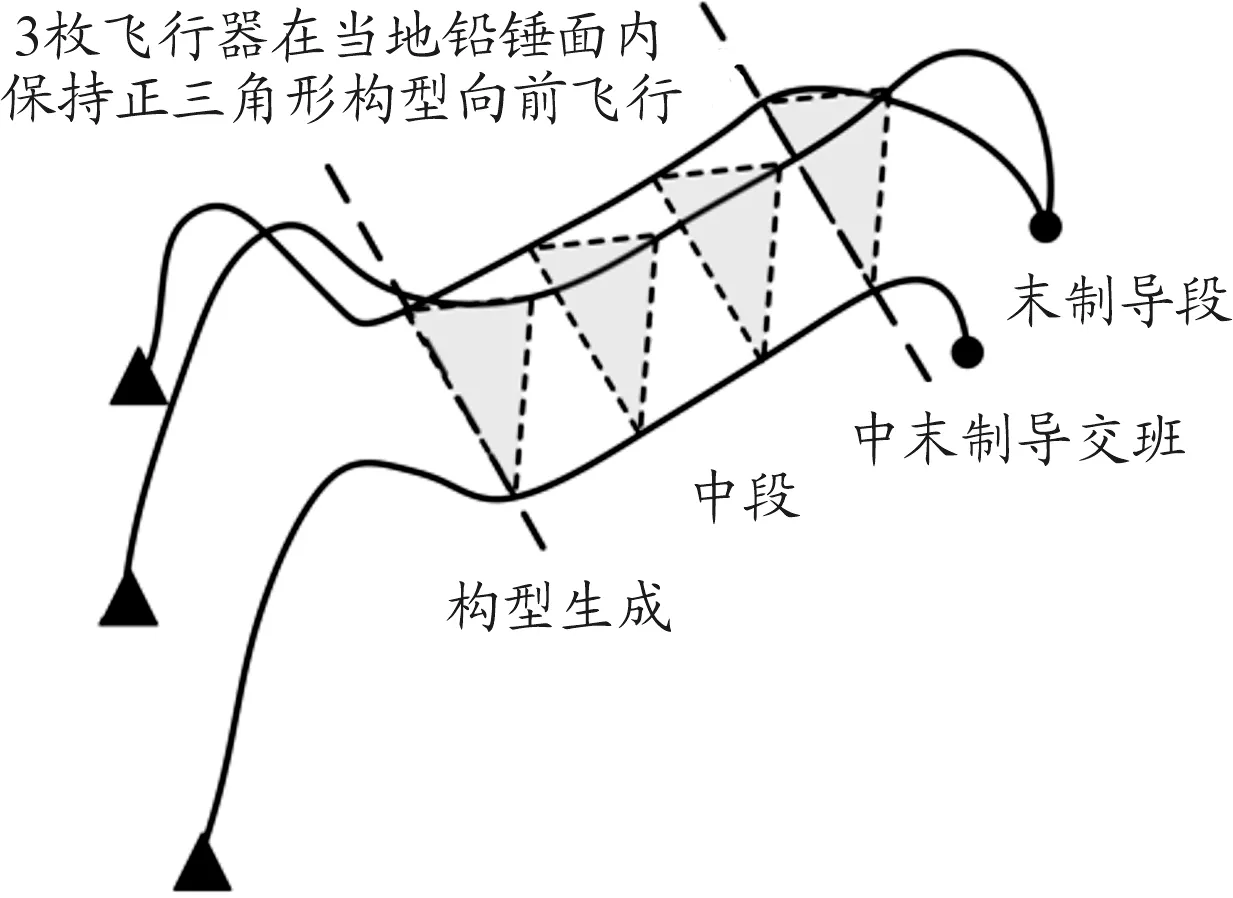
圖1 本文欲解決的構型保持問題示意圖

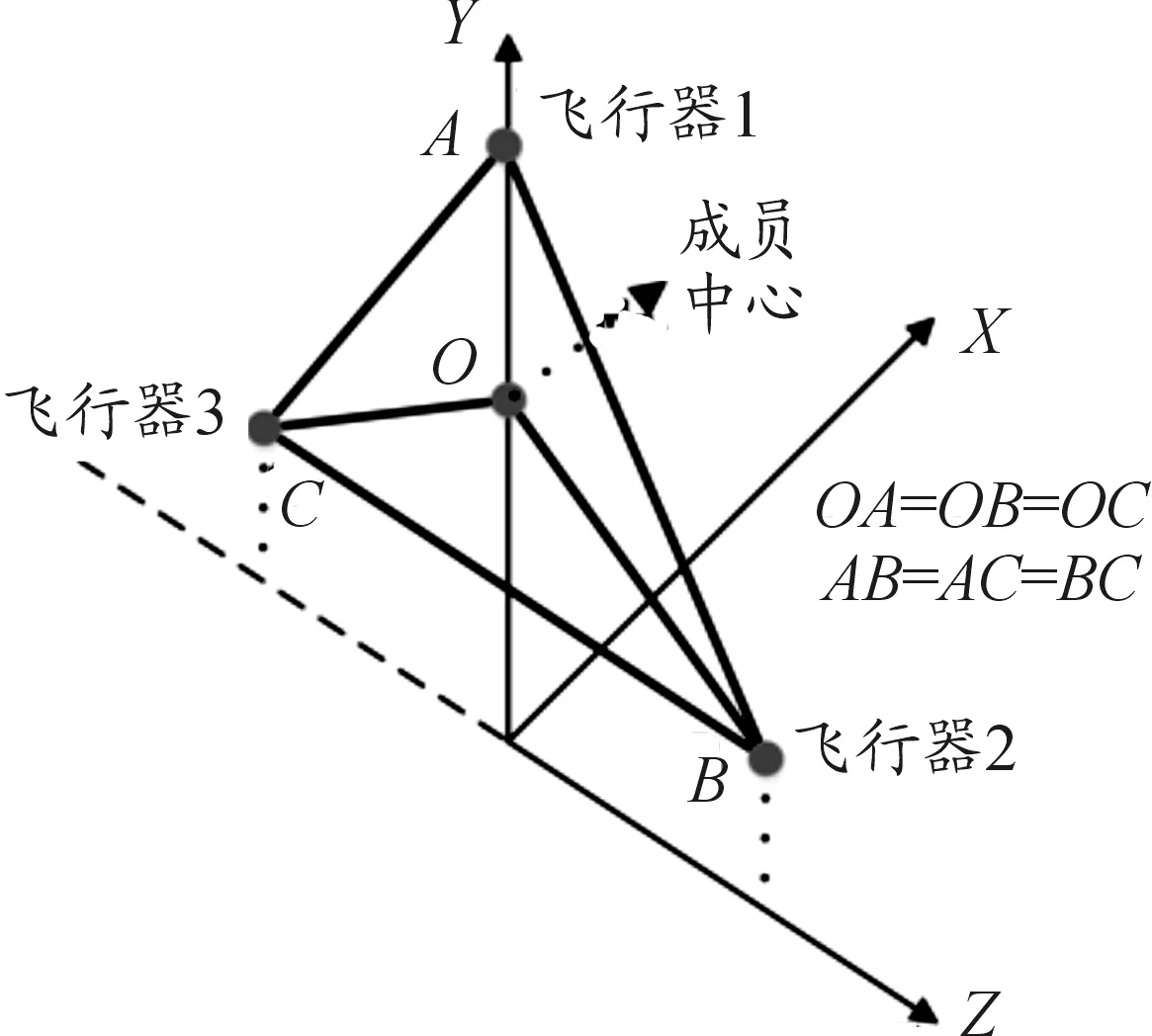
圖2 構型保持示意圖

評判構型保持的效果用如下方式表示：在圖3中，藍色點是飛行器當前位置，成員中心為黑色點，在鉛錘面內以黑色點為中心構造正三角形，認為此三角形的3個頂點為3個飛行器的期望位置。則各飛行器實際位置與期望位置的距離認為是構型保持的誤差。

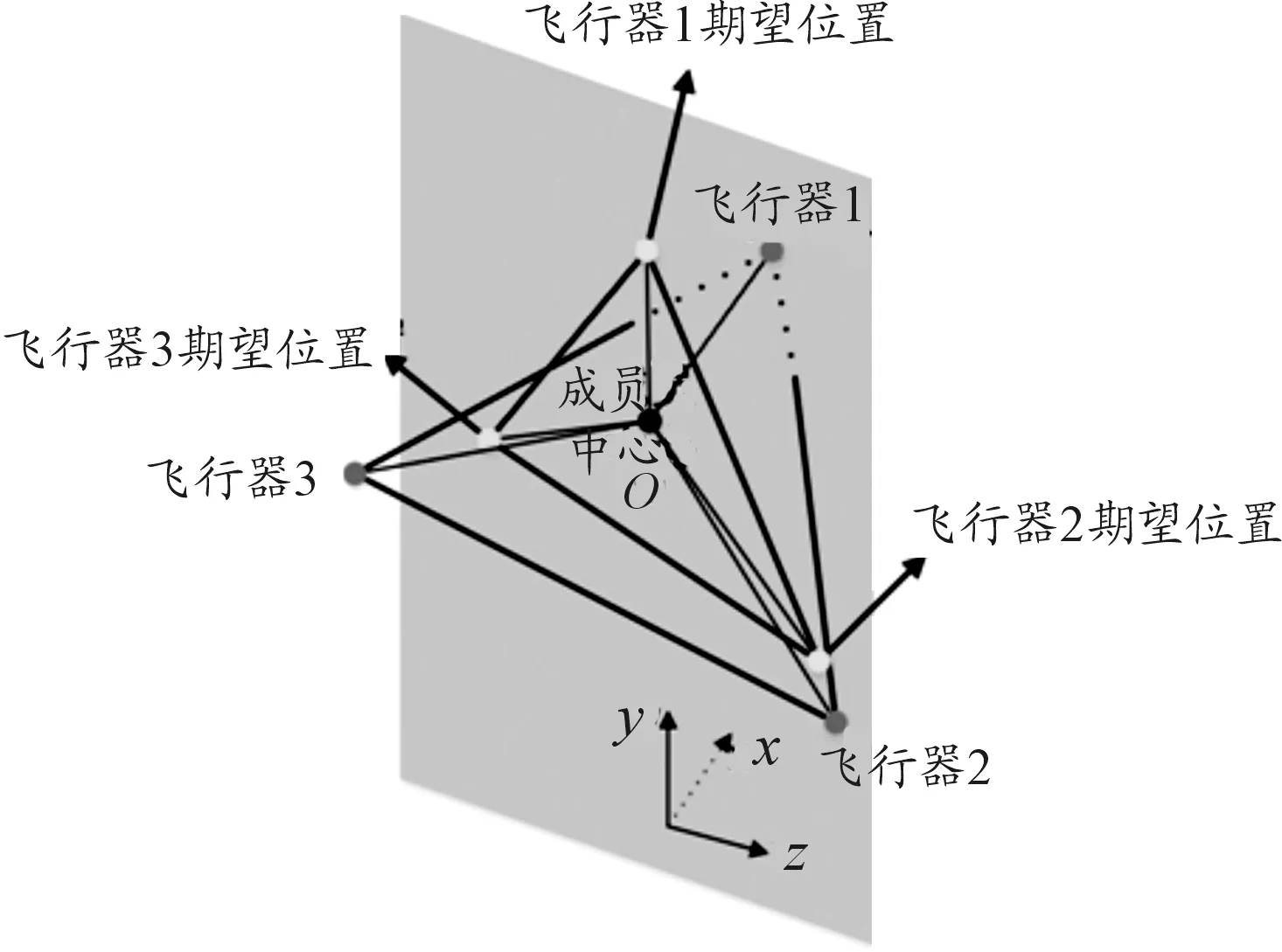
圖3 構型保持誤差示意圖

飛行器的動力學模型如式(1)所示：

sinψ=cosαcosβsinσ-sinαcosσsinν+

cosαsinβcosσcosν

sinφcosψ=cosαcosβsinθcosσ+

sinα(cosθcosν+sinθsinσsinν)-

cosαsinβ(-cosθsinν+sinθsinσcosν)

sinγcosψ=sinαcosβsinσ+cosαcosσsinν+

sinαsinβcosσcosν

(1)

式(1)為飛行器基本的動力學方程，由于與本文研究內容不直接相關，所以不詳細介紹(可詳見文獻[1])。這里需要指出的是，上述動力學模型的控制指令是攻角αc和傾側角γc，控制飛行器飛行的方式是每隔固定時間間隔(如 0.5 s)給出一次指令，即通過設計這兩個量在每次數值積分時的值(數值積分的步長等于指令時間間隔)，來解決本文旨在解決的問題。

此控制指令已經通過傳統優化方法(后面簡稱“優化法(FKCG)”)得到并且實現了構型保持，其效果見圖4，但是存在一個重要缺陷：優化法的速度慢，計算量大，在python環境下優化一次需約2.3 s，難以滿足飛行器飛行高速高動態對指令快速在線生成的要求。因此針對這一缺陷，本文旨在設計一個深度神經網絡模型以快速生成控制指令。

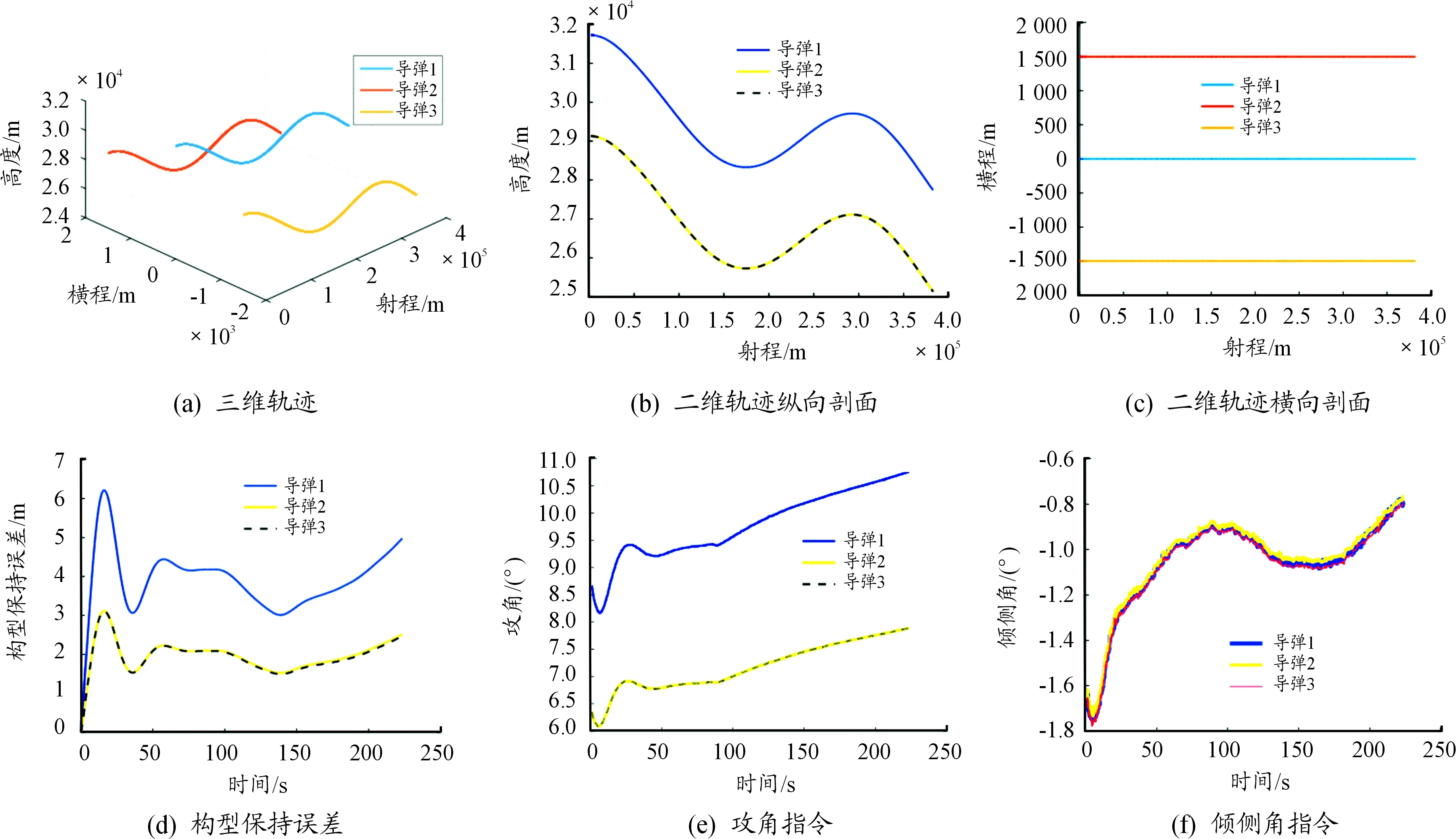
圖4 成功構型保持效果的實例曲線

2 基于深度卷積神經網絡的構型保持模型

2.1 深度神經網絡模型

1) 輸入。對每枚飛行器選取17個狀態變量作為輸入，共51個變量。同時借鑒機器視覺中圖像用像素矩陣元素表示的做法，將其組合為8*8矩陣，剩余8×8-51=13個空格均置零，如圖5所示。

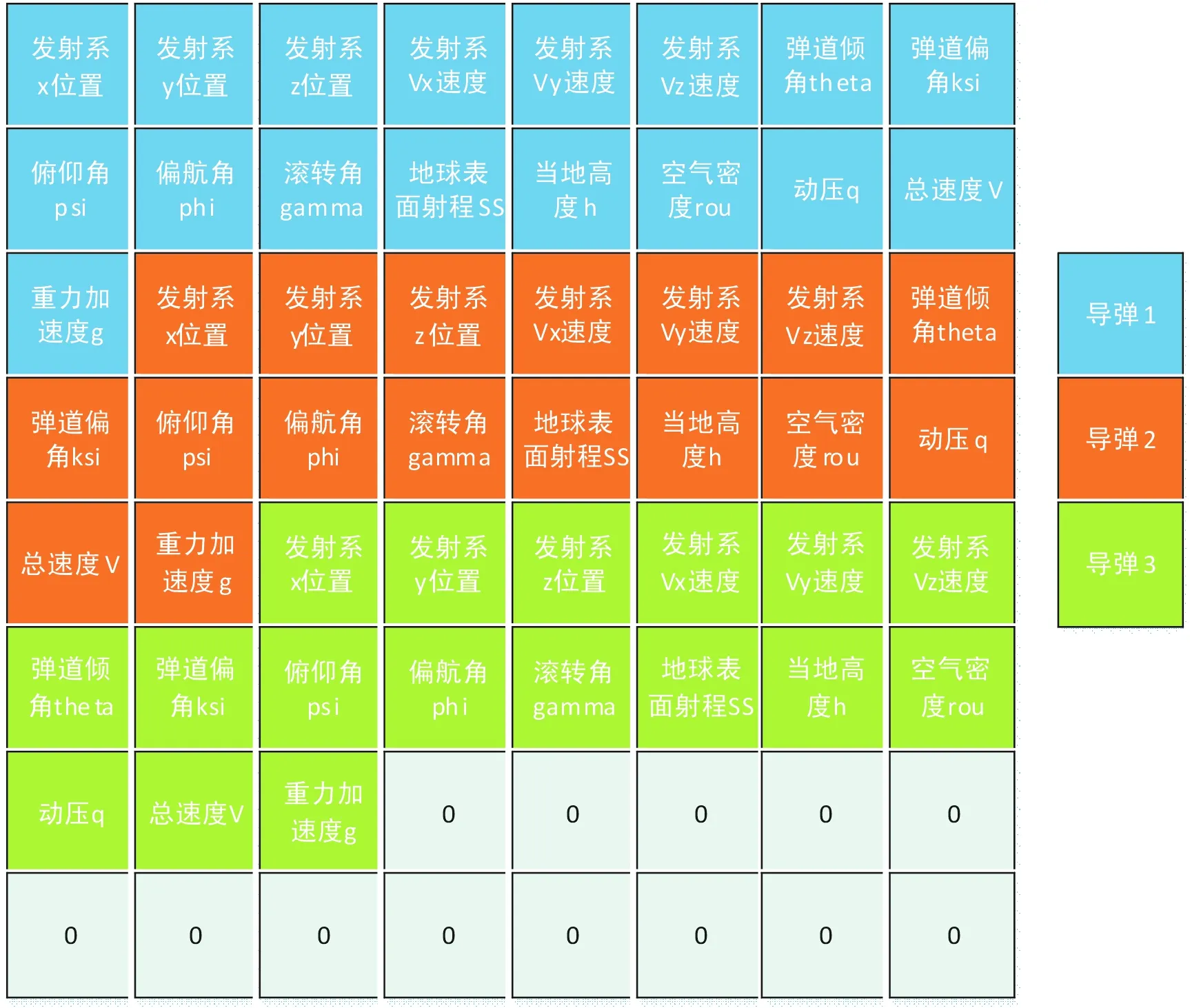
圖5 輸入矩陣元素

2) 輸出。輸出為3個飛行器的控制指令，即3個攻角3個傾側角。

3) 神經網絡模型。設計神經網絡模型時有以下5項考慮：

① 由于飛行器動力學模型為強非線性的復雜模型，因此選取神經網絡的深度即層數時，不能因模型容量小而導致欠擬合；

② 加深網絡深度后，為避免層數加深反而學習效果未提升甚至衰減的現象，引入“殘差結構”和“歸一化層”；

③ 采取卷積神經網絡和全連接層進行特征提取；

④ 由于輸入矩陣不同于圖像矩陣中像素有連續性，因此不考慮降低敏感性及保留主要特征，這里卷積層后不連接池化層；

⑤ 輸出層采取并聯結構，分別輸出攻角和傾側角。

最終，經過對比試驗和綜合選擇，搭建了19層神經網絡，如圖6所示。其中，conv代表卷積層，均使用3*3卷積核，步幅為1，填充為1；BatchNorm代表批量歸一化層；Activation 代表激活層，均采用Tanh函數；Dense代表全連接層；每個方塊最后面的數字代表輸出的通道數。

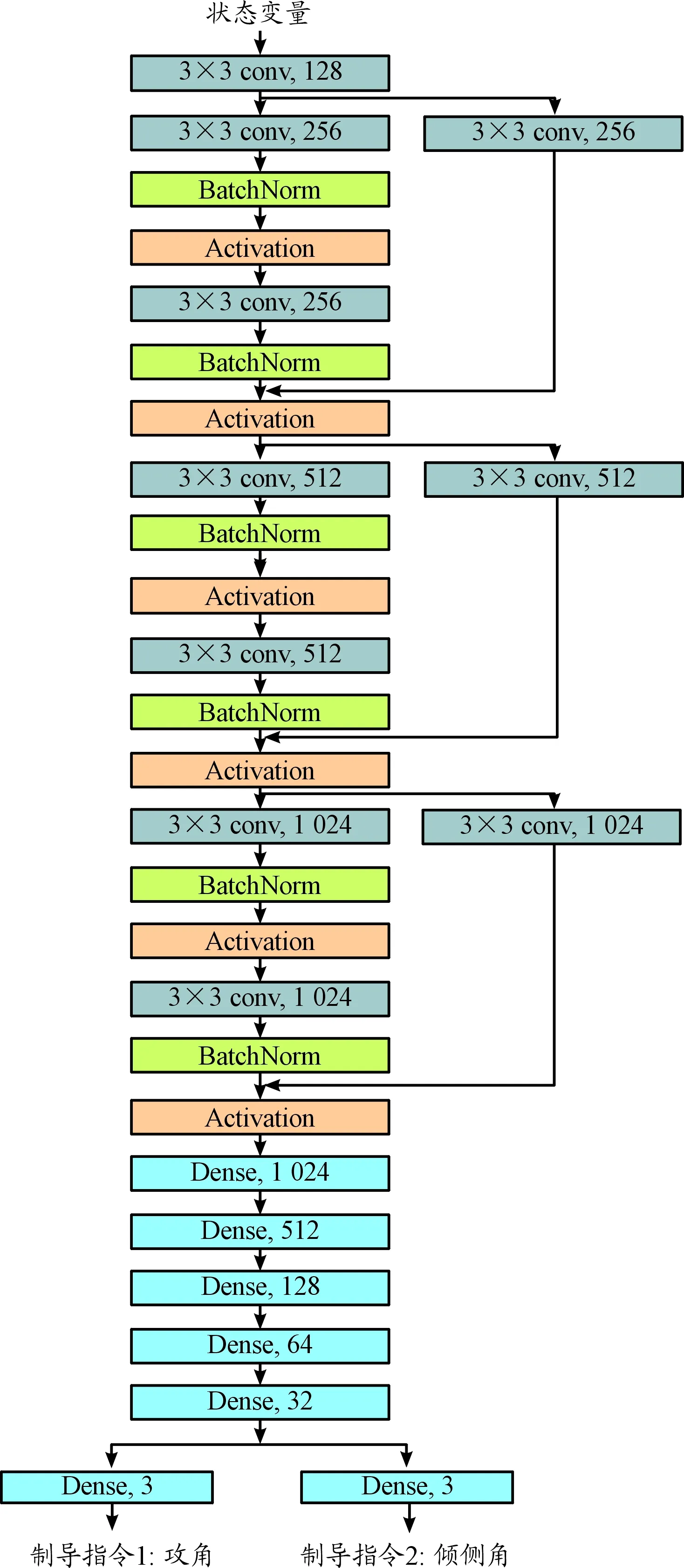
圖6 神經網絡模型結構示意圖

2.2 模型訓練

1) 訓練方法。模型訓練的損失函數采取誤差平方，正則化采用權重衰減懲罰項，衰減系數為0.000 1，損失函數如式(2)所示。

(2)

其中，αi和νi為神經網絡輸出；αic和νic為樣本輸出。這里定義訓練誤差為(L/6)0.5*57.3，其物理意義是角度制下6個角度的平均誤差。

模型訓練的優化方法采取小批量隨機梯度下降法，由于輸出為弧度制角度，數值較小，因此學習率應設置較小以敏感微小變化，初始值為0.1。為避免學習率過大導致訓練結果持續震蕩但不衰減，考慮當訓練誤差在近20個周期內的標準差小于某一設定值(0.002°)時，縮小學習率以使訓練誤差能夠減小；如果近50個周期內訓練誤差的標準差小于某一設定值(0.002°)，認為此時模型訓練誤差無法再繼續減小，即已到模型擬合準確程度的上限，停止訓練。上述學習率縮減及訓練終止條件如圖7所示。訓練硬件采用阿里ecs.g5.large型云服務器。

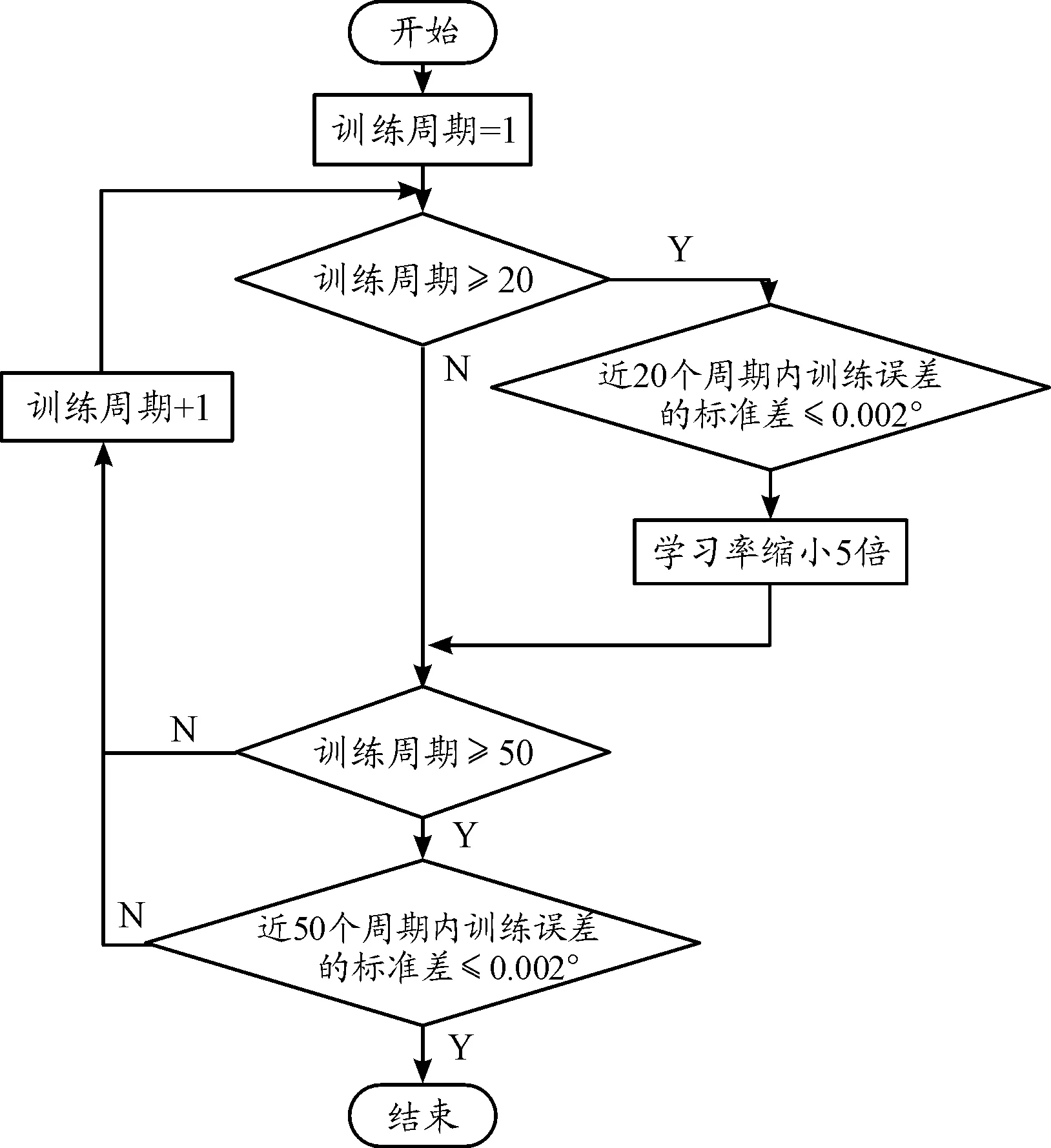
圖7 訓練終止條件框圖

2) 訓練結果。以成功構型保持的實例即圖4作為訓練樣本，訓練結果如圖8、圖9所示。

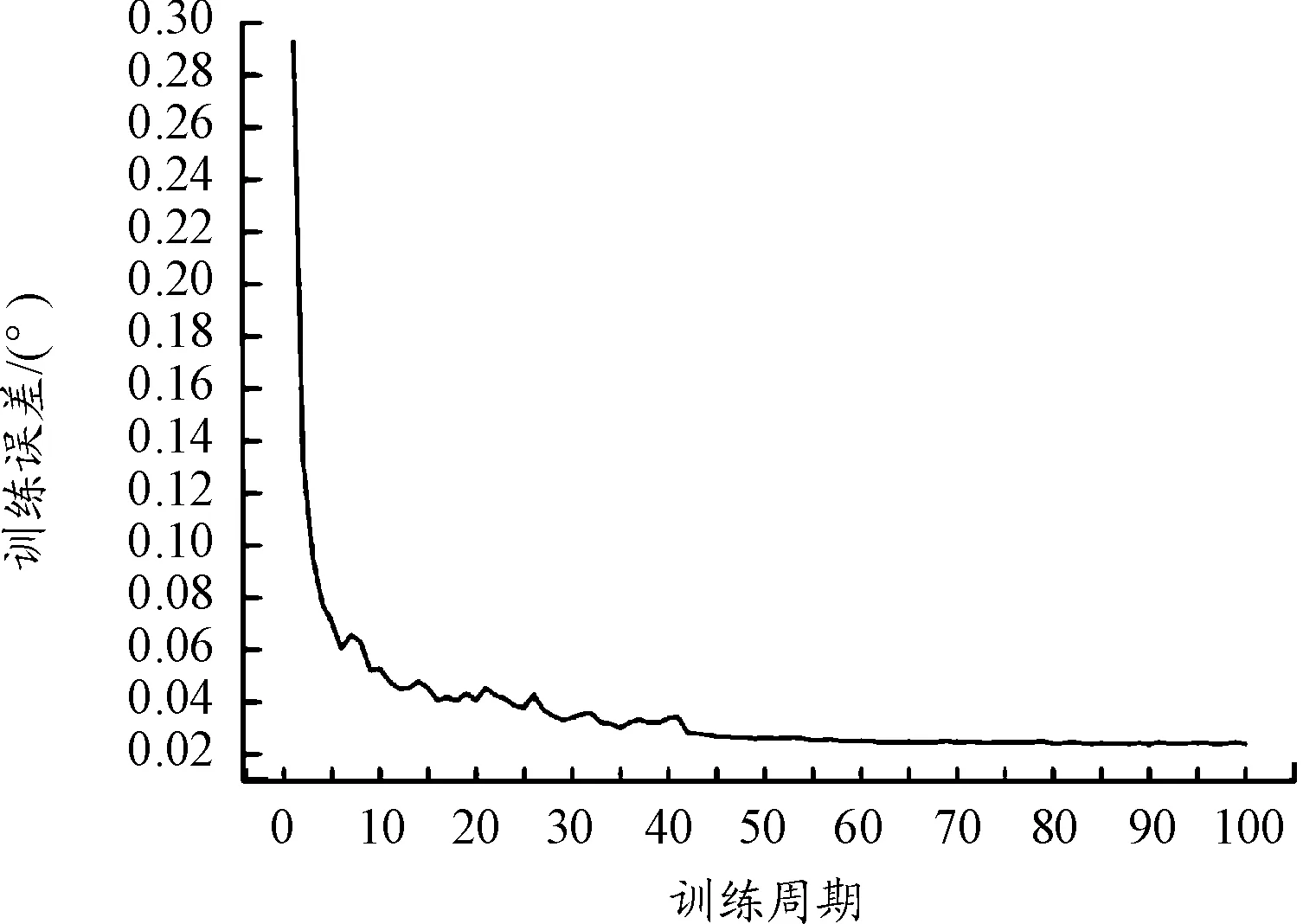
圖8 訓練誤差曲線

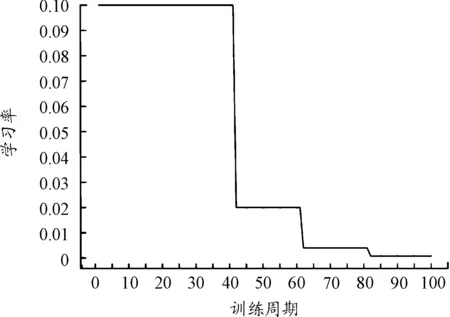
圖9 學習率曲線

在圖8中，訓練誤差持續減小，最終穩定于0.025°附近，其物理意義是攻角或傾側角在神經網絡的輸出值與樣本值僅相差約0.025°，對于這兩個角度物理量，這個量級十分小，這一結果驗證了深度神經網絡模型和訓練方法的有效性。在圖9中，可以看到學習率經歷了3次縮減，第一次縮減帶來訓練誤差明顯下降，但后兩次沒有，這就說明此時已經不是由于學習率過大導致訓練誤差無法減小，而是已經到達模型擬合的能力上限，同時結合圖8也驗證了學習率縮減策略的有效性。

3 泛化誤差累積與校正

3.1 泛化誤差累積

神經網絡的泛化誤差是不可避免的，并且永遠大于訓練誤差。當這個誤差足夠小時，例如在圖像分類中我們可以認為大部分情況下圖像分類正確，只有一小部分分類錯誤。但是在飛行器運動問題中，控制指令攻角αc和傾側角γc是每隔固定時間間隔就給出一次，一段飛行軌跡一般存在上萬個這樣的間隔，所以當上萬次指令都存在泛化誤差時，盡管每次誤差的量級可能很小(10-2度)，但泛化誤差累積仍會對飛行器運動帶來明顯影響。

圖10是只使用神經網絡解算控制指令得到的飛行器軌跡，可以看到此時彈道已發生整體偏移，并且此時3個飛行器的構型保持誤差持續上升。

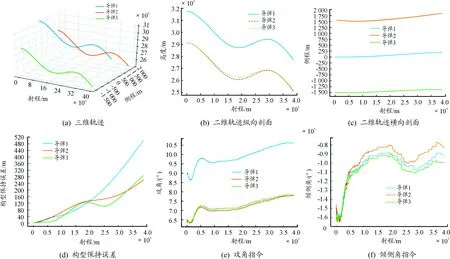
圖10 泛化誤差累積對飛行器軌跡的影響曲線

3.2 校正

針對泛化誤差累積對飛行器運動帶來顯著影響這一問題，考慮采取以下設計來校正累積的泛化誤差：

1) 對神經網絡解算的控制指令加上一個校正量，以解決泛化誤差累積的問題；

2) 校正量的值是優化法解算的控制指令與神經網絡輸出控制指令的差值；

3) 校正量每隔n個制導周期重新計算1次；

4) 認為校正周期計算得的校正量能夠近似代表校正后n個周期內神經網絡與優化法解算的差值。

最終，“智能-校正”算法如圖11所示，第4節將敘述其構型保持效果。

圖11 “智能-校正”算法示意圖

4 仿真分析

本節針對不同的n進行仿真，當n=0時，即每個周期都校正，即為純優化解算控制指令，其仿真結果如圖4所示；當n=∞，相當于不校正，即為純神經網絡解算控制指令，其仿真結果如圖10所示。這里一個周期為0.01 s，則當n=100時即每間隔1 s進行一次校正。可以直觀判斷，n越小，校正越頻繁，泛化誤差累積的影響越小，構型保持效果越好。

這里給出n取不同值時的構型保持誤差如表1所示，和n=50、100、130的飛行器軌跡分別如圖12～圖14所示。

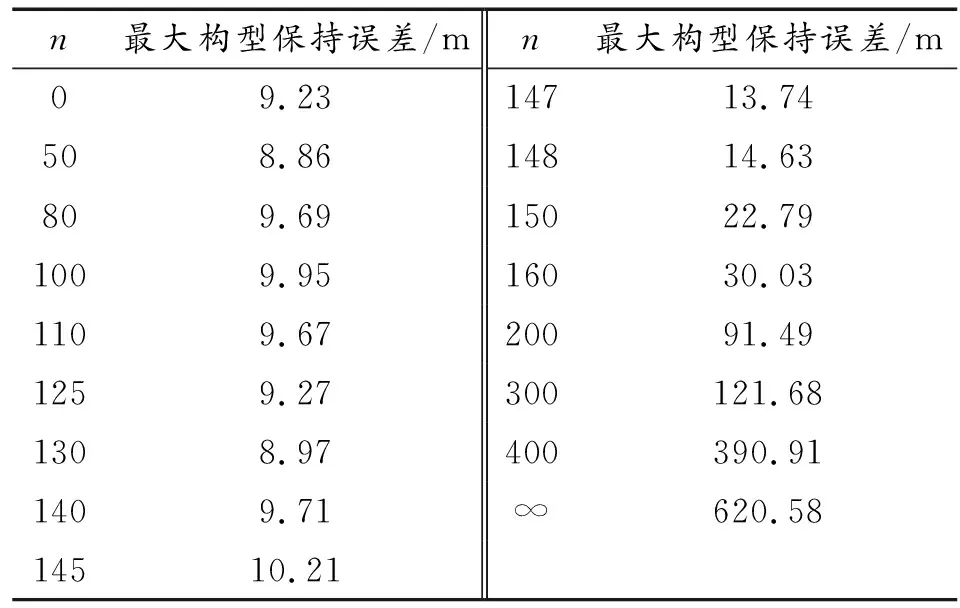
表1 不同n下構型保持誤差

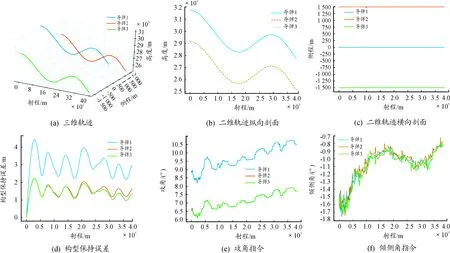
圖12 n=50時的仿真曲線

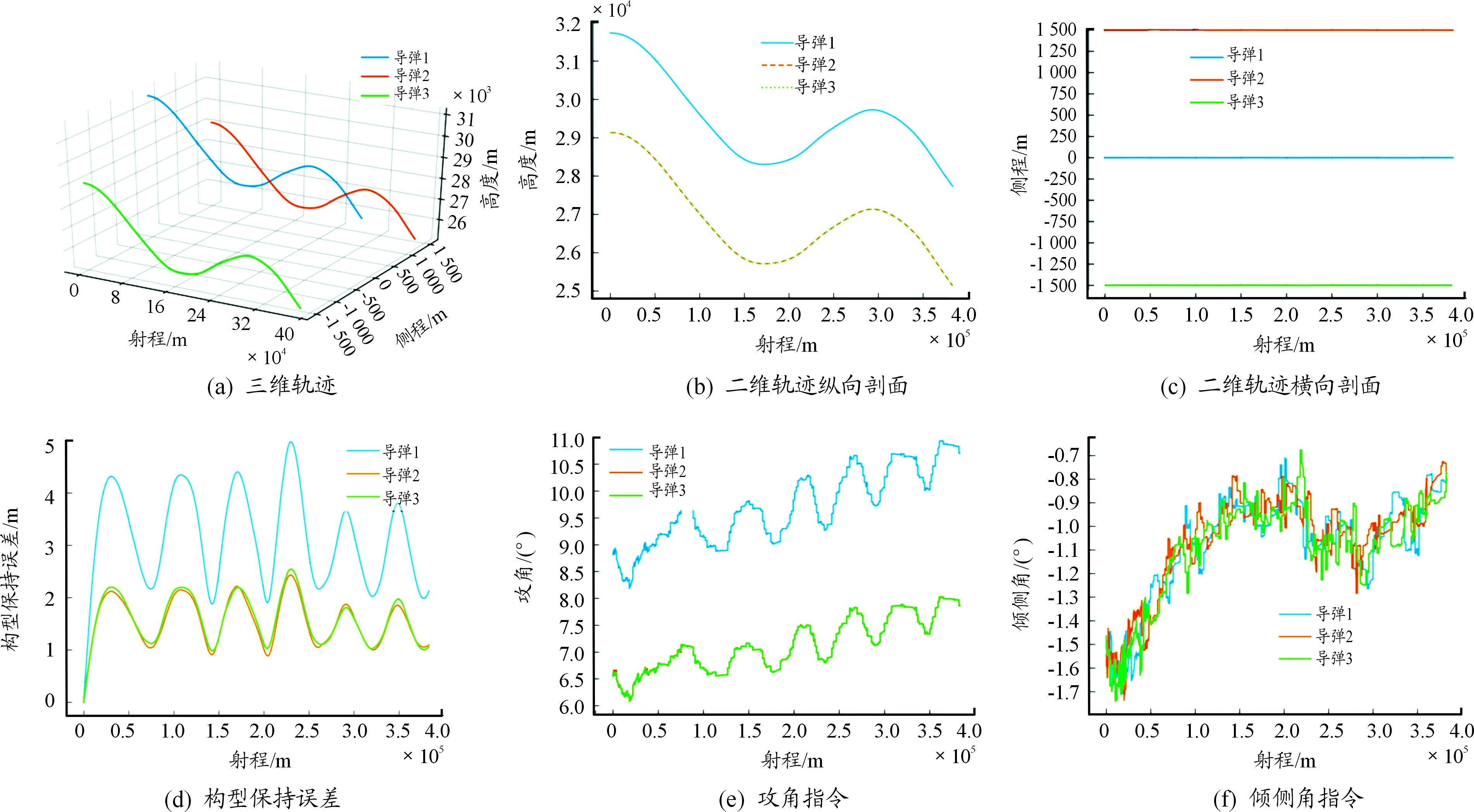
圖13 n=100時的仿真曲線

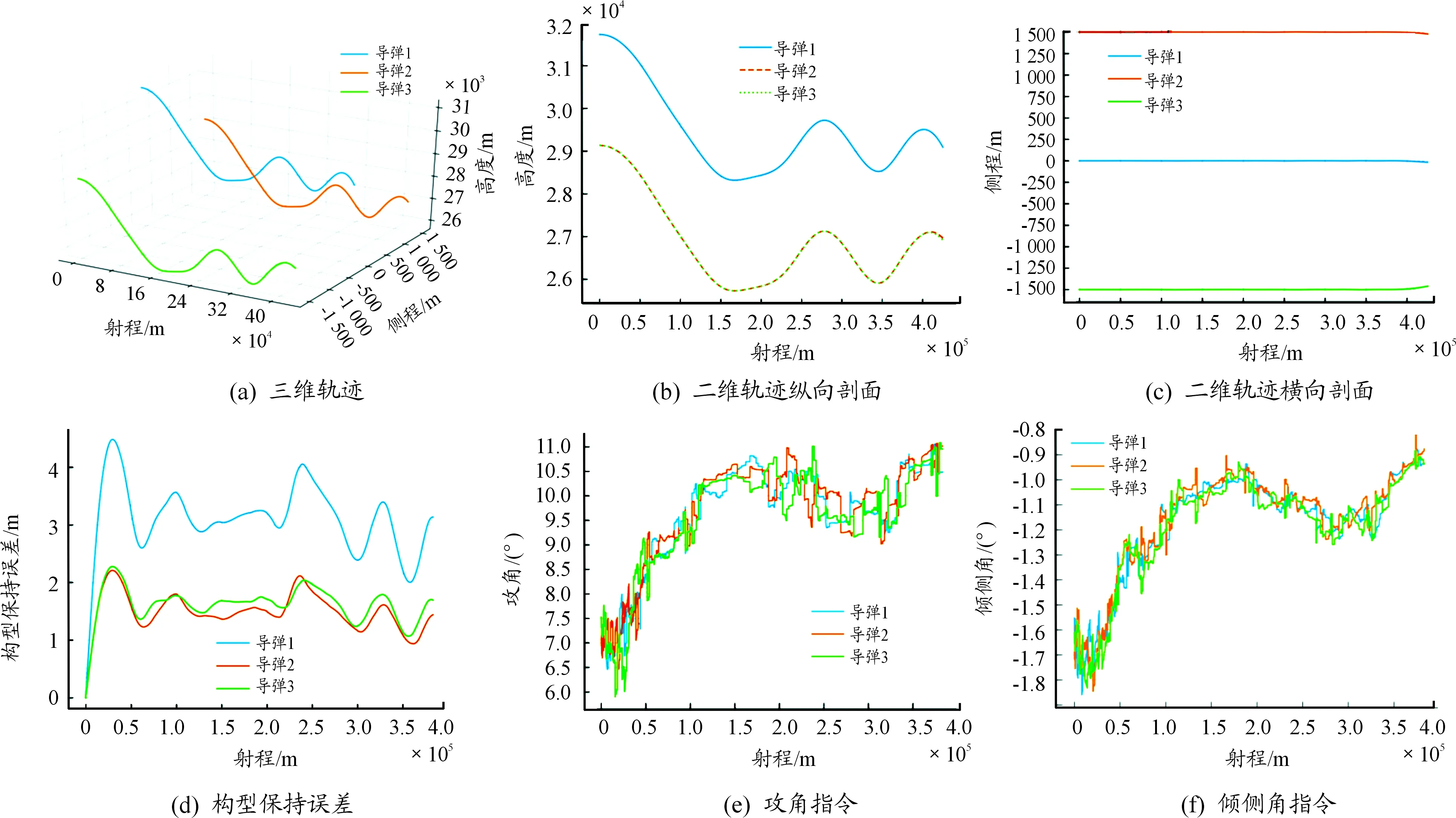
圖14 n=130時的仿真曲線

從以上仿真結果可以看出：

1) “智能-校正”算法解決了泛化誤差累積的問題，仿真結果驗證了其有效性；

2) 當n≤140時，“智能-校正”算法的構型保持誤差之和基本不變，維持在一個較小數量(均小于10 m)；

3) 當n>140后，隨著校正間隔越來越長，泛化誤差累積的影響越來愈大，構型保持誤差持續上升，直到n=∞(不校正，純神經網絡)，構型保持誤差之和為620.58m；

4) 考慮計算速度，仿真時我們采取相同的計算條件(Python語言、PyCharm平臺、MXNet框架)，神經網絡輸出一次控制指令的時間約為0.38 s，而原優化方法解算一次控制指令的時間約為2.3 s，速度提升了約6倍。這一結果實現了本文設計神經網絡的初衷：快速生成控制指令；

可以說，基于深度神經網絡的智能-校正算法兼顧了精度和速度。精度方面，通過校正消除了泛化誤差累積的影響，實現了較小構型保持誤差；速度方面，原優化方法解算一次指令需約2.3 s，而神經網絡解算一次指令只需約0.23 s，速度提升了約6倍。同時給出了不同校正間隔時間與構型保持誤差的關系，當對構型保持誤差要求不高時，可適當增大校正間隔時間以帶來更少的計算量；反之需高精度構型保持時，可減小校正間隔時間。

5 結論

基于卷積層、全連接層、歸一化層和殘差網絡設計了一個19層深度神經網絡，并采用權重衰減正則項和可變學習率，成功將神經網絡訓練誤差降低至約0.025°。神經網絡應用于飛行器制導過程時，存在泛化誤差累積的現象，對此設計校正環節以避免帶來構型保持誤差。通過飛行仿真驗證了“智能-校正”算法的快速性和有效性，給出了不同校正間隔時間與構型保持誤差的關系。